Skip to content

Latest commit

 

History

History
91 lines (74 loc) · 4.32 KB

README.md

File metadata and controls

91 lines (74 loc) · 4.32 KB
Raw

MinSizeKmeans

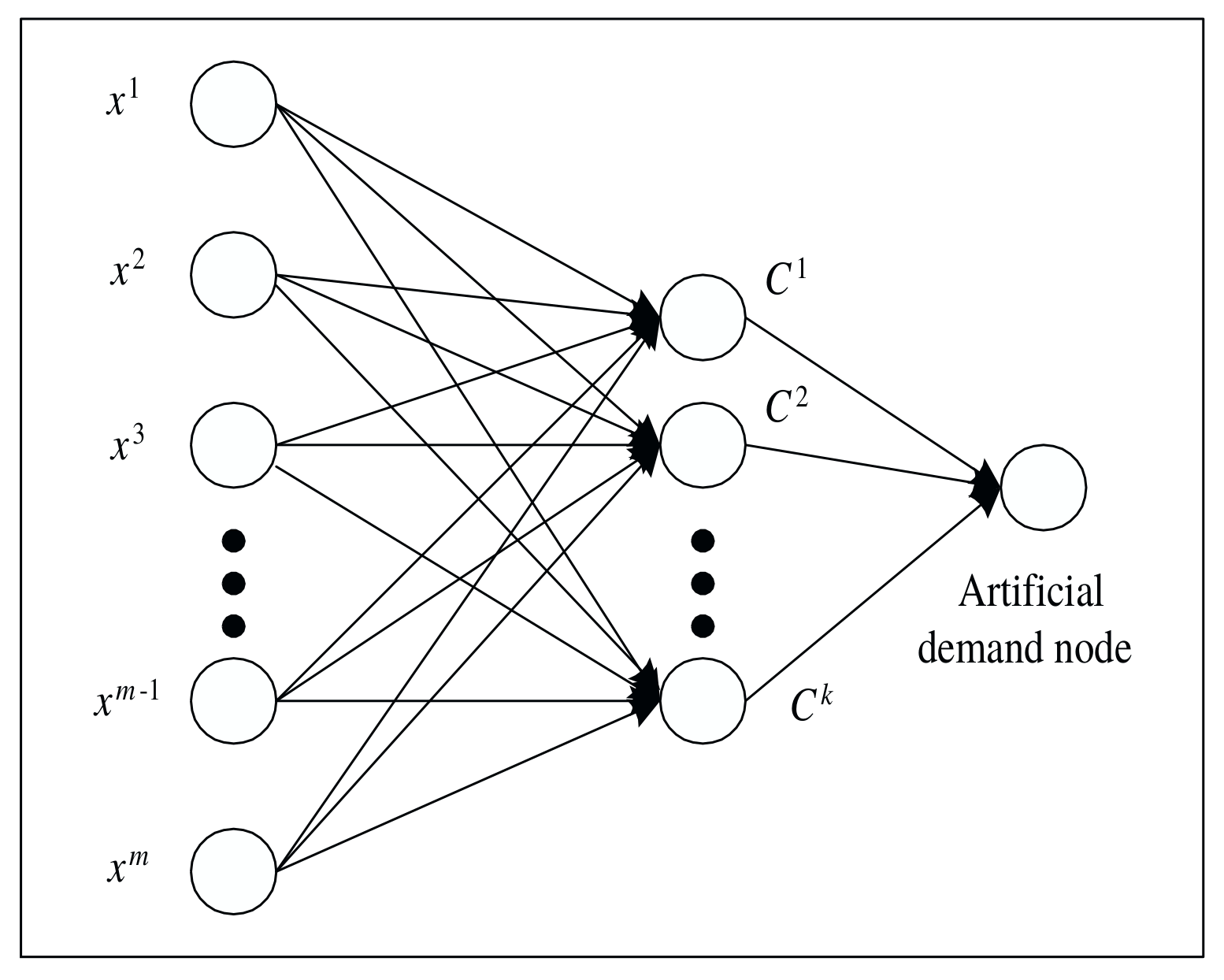
A python implementation of KMeans clustering with minimum cluster size constraint (Bradley et al., 2000)[1]

Note that the paper suggests using a dedicated minimum-cost network flow algorithm for solving the subproblem, but in my implementation I use standard MIP solvers. My motivation for doing so was this comment from Tobias Achterberg:

If you have a pure network, then the constraint matrix is totally unimodular, so any vertex solution will be integral. And since the simplex algorithm always returns a vertex solution (if one exists), your solution will be integral.

Note that in our experience, a network simplex algorithm is not faster than the dual simplex, which is the reason why Gurobi does not provide a network simplex.

Usage

usage: run_mskmeans.py [-h] [-n NUM_ITER] [-o OUTFILE] datafile k min_size

positional arguments:
  datafile              file containing the coordinates of instances
  k                     number of clusters
  min_size              minimum size of each cluster

optional arguments:
  -h, --help            show this help message and exit
  -n NUM_ITER, --NUM_ITER NUM_ITER
                        run the algorithm for NUM_ITER times and return the best clustering
  -o OUTFILE, --OUTFILE OUTFILE
                        store the result in OUTFILE

To see a run of algorithm on example data, run the script example_run.sh in minsize_kmeans directory.

Dependencies

This program uses Pulp to solve the assignment subproblem. You should also have a MIP solver (Gurobi, Cplex, Cbc, etc.) installed and have it configured to work with Pulp.

Extension

This algorithm can be easily extended to account for a constraint on maximum number of instances in a cluster. To do so, in the network flow formulation of [1], we add constraints on the capacity of arcs that enter the sink node.

To run the algorithm with both minimum and maximum size constraints, use this command:

usage: minmax_kmeans.py [-h] [-n NUM_ITER] [-o OUTFILE] datafile k min_size max_size

positional arguments:
  datafile              file containing the coordinates of instances
  k                     number of clusters
  min_size              minimum size of each cluster
  max_size              maximum size of each cluster

optional arguments:
  -h, --help            show this help message and exit
  -n NUM_ITER, --NUM_ITER NUM_ITER
                        run the algorithm for NUM_ITER times and return the best clustering
  -o OUTFILE, --OUTFILE OUTFILE
                        store the result in OUTFILE

An example run is included in the script example_run.sh in minsize_kmeans directory.

Constrained K-Means with Weighted Instances

Sometimes instead of the size of clusters, we want to constrain the total weight of instances that are in each cluster. Unfortunately, the subproblem for constrained k-means in this case will be NP-complete. However, we can still give this subproblem to a MIP solver and hope that it will be solved in a reasonable time. To run this algorithm, use this command:

usage: weighted_mm_kmeans.py [-h] [-n NUM_ITER] [-o OUTFILE]
                             datafile k weightfile min_weight max_weight

positional arguments:
  datafile              file containing the coordinates of instances
  k                     number of clusters
  weightfile            file containing the weights of instances
  min_weight            minimum total weight for each cluster
  max_weight            maximum total weigth for each cluster

optional arguments:
  -h, --help            show this help message and exit
  -n NUM_ITER, --NUM_ITER NUM_ITER
                        run the algorithm for NUM_ITER times and return the best clustering
  -o OUTFILE, --OUTFILE OUTFILE
                        store the result in OUTFILE

An example run is included in the script example_weighted.sh in minsize_kmeans directory.

References

  1. Bradley, P. S., K. P. Bennett, and Ayhan Demiriz. "Constrained k-means clustering." Microsoft Research, Redmond (2000): 1-8.