diff --git a/.nojekyll b/.nojekyll new file mode 100644 index 0000000..e69de29 diff --git a/404.html b/404.html new file mode 100644 index 0000000..eee5687 --- /dev/null +++ b/404.html @@ -0,0 +1,1699 @@ + + + + + + + + + + + + + + + + + + + catflow + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ +
+
+ +
+ + + + + + + + +
+ + + + + + + +
+ +
+ + + + +
+
+ + + +
+
+
+ + + + + + + +
+
+
+ + + +
+
+
+ + + +
+
+
+ + + +
+
+ +

404 - Not found

+ +
+
+ + +
+ + + +
+ + + +
+
+
+
+ + + + + + + + + + + + + + + + \ No newline at end of file diff --git a/Usage/cluster_structures/index.html b/Usage/cluster_structures/index.html new file mode 100644 index 0000000..36734a1 --- /dev/null +++ b/Usage/cluster_structures/index.html @@ -0,0 +1,1909 @@ + + + + + + + + + + + + + + + + + + + + + + + + + 团簇结构分析 - catflow + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + Skip to content + + +
+
+ +
+ + + + + + + + +
+ + + + + + + +
+ +
+ + + + +
+
+ + + +
+
+
+ + + + + + + +
+
+
+ + + +
+
+
+ + + +
+
+
+ + + +
+
+ + + + + + + +

团簇结构分析

+

载入团簇结构

+

首先将需要分析的团簇轨迹文件读入到程序中，用户可以指定 path 参数为文件路径， +其他的参数请以可选参数形式传入。

+
from catflow.structure.cluster import Cluster
+
+trajfile = "./dump.lammpstrj"
+c = Cluster(trajfile, topology_format="LAMMPSDUMP", dt=0.0005)
+
+
+

提示

+

注意默认的格式为"XYZ"，如需要导入其他格式，请参考 +MDAnalysis文档。

+
+

或将 MDAnalysis 的一个 Universe 实例导入：

+
from MDAnalysis import Universe
+u = Universe(trajfile, topology_format="LAMMPSDUMP", dt=0.0005))
+d = Cluster.convert_universe(u)
+
+

Lindemann Index 计算

+

为分析体系的相变性质，Lindemann等人[1]提出了对结构随时间均方键长的演变进行分析来确定相变性质的方法， +一般计算公式如下：

+
\[< q_i >_{atoms} = \frac{1}{N(N-1)} \frac{\sqrt{<r^2_{ij}> - <r_{ij}>^2}}{<r_{ij}>}\]
+

这里参照 Welford 算法[2]计算方差，简单实现了 Lindemann Index的计算方法，调用如下：

+
lpf = c.lindemann_per_frames(u, select_lang="name Pt")
+
+

即可得到关于整条轨迹Lindemann index的变化趋势，对 lpf 作图，可以帮助判断相变情况以及确定MD是否收敛。

+

注意这里 lindemann_per_frames 读入的是MDAnalysis中的Universe对象，通常用 select_lang 来指定需要对哪些原子进行分析， +即给定对应的Atom selection language来选取， +请参考官方文档的说明。

+

拟合

+

为对团簇相变行为的温度依赖进行分析，常对得到的曲线进行拟合，可以采用如下函数，以dataframe形式输出拟合的曲线：

+
import numpy as np
+
+temperature = np.array([300., 400., 500., 600., 700.])
+lindemann = np.array([0.05, 0.10, 0.20, 0.25, 0.32])
+bounds = ([-np.inf, -np.inf, -np.inf, -np.inf, 400, 15.], 
+          [np.inf, np.inf, np.inf, np.inf, 700., 100.])
+df = fitting_lindemann_curve(temperature, lindemann, bounds, function='func2')
+
+

其中，

+
    +
  • func1函数形式为： + $$ f(x) = b + (a - b) x + \frac{d}{1 + \exp({\frac{x - x_0}{\mathrm{d}x})}} + cx $$
    • +
  • func2函数形式为 + $$ f(x) = \frac{ax+b}{1 + \exp({\frac{x - x_0}{\mathrm{d}x})}} + \frac{cx+d}{1 + \exp({\frac{x_0 - x}{\mathrm{d}x})}}$$
    • +
+

默认采用 func2 进行拟合，bounds中上下界的参数对应即为a, b, c, d, x0, dx的取值范围。

+

References

+

[1] F. A. Lindemann, Zeitschrift für, Phys. 1910, 11, 609–612.

+

[2] Donald E. Knuth, The art of computer programming, volume 2 (3rd ed.): seminumerical algorithms, Addison-Wesley Longman Publishing Co, 1997, 232.

+ + + + + + +
+
+ + +
+ + + +
+ + + +
+
+
+
+ + + + + + + + + + + + + + + + \ No newline at end of file diff --git a/Usage/dpgen_analysis/index.html b/Usage/dpgen_analysis/index.html new file mode 100644 index 0000000..b143c87 --- /dev/null +++ b/Usage/dpgen_analysis/index.html @@ -0,0 +1,1919 @@ + + + + + + + + + + + + + + + + + + + + + + + + + 分析DP-GEN任务 - catflow + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + Skip to content + + +
+
+ +
+ + + + + + + + +
+ + + + + + + +
+ +
+ + + + +
+
+ + + +
+
+
+ + + + + + + +
+
+
+ + + +
+
+
+ + + +
+
+
+ + + +
+
+ + + + + + + +

分析DP-GEN任务

+

加载环境

+

首先，导入环境：

+
from catflow.tesla.dpgen import DPTask
+
+

加载DP-GEN工作目录：

+
t = DPTask(
+    path='/path/to/dpgen/', 
+    param_file='param.json', 
+    machine_file='machine.json',
+    record_file='record.dpgen'
+)
+
+

便可根据所需分析的部分，对训练情况进行分析。

+

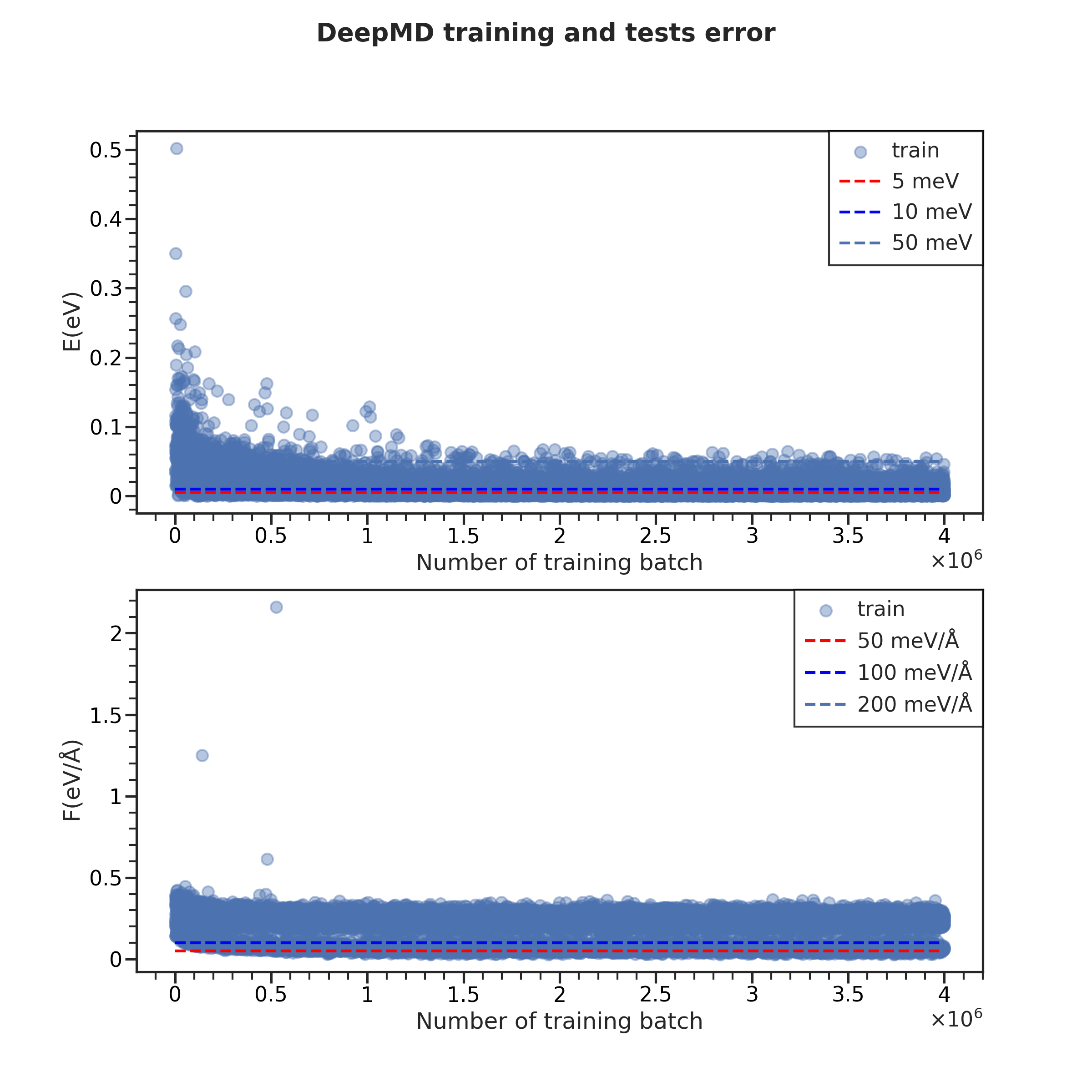
训练（Training）

+

导入分析器（DPAnalyzer），这里我们选择训练，即：

+
from catflow.tesla.dpgen.training import DPTrainingAnalyzer
+
+

从任务初始化分析器实例：

+
ana = DPTrainingAnalyzer(t)
+
+

即可利用ana的内置函数进行作图：

+
fig = ana.plot_lcurve(
+    iteration=28, test=False, style='ticks', context='talk'
+)
+fig.set_size_inches((12,12))
+
+

20221110160809

+

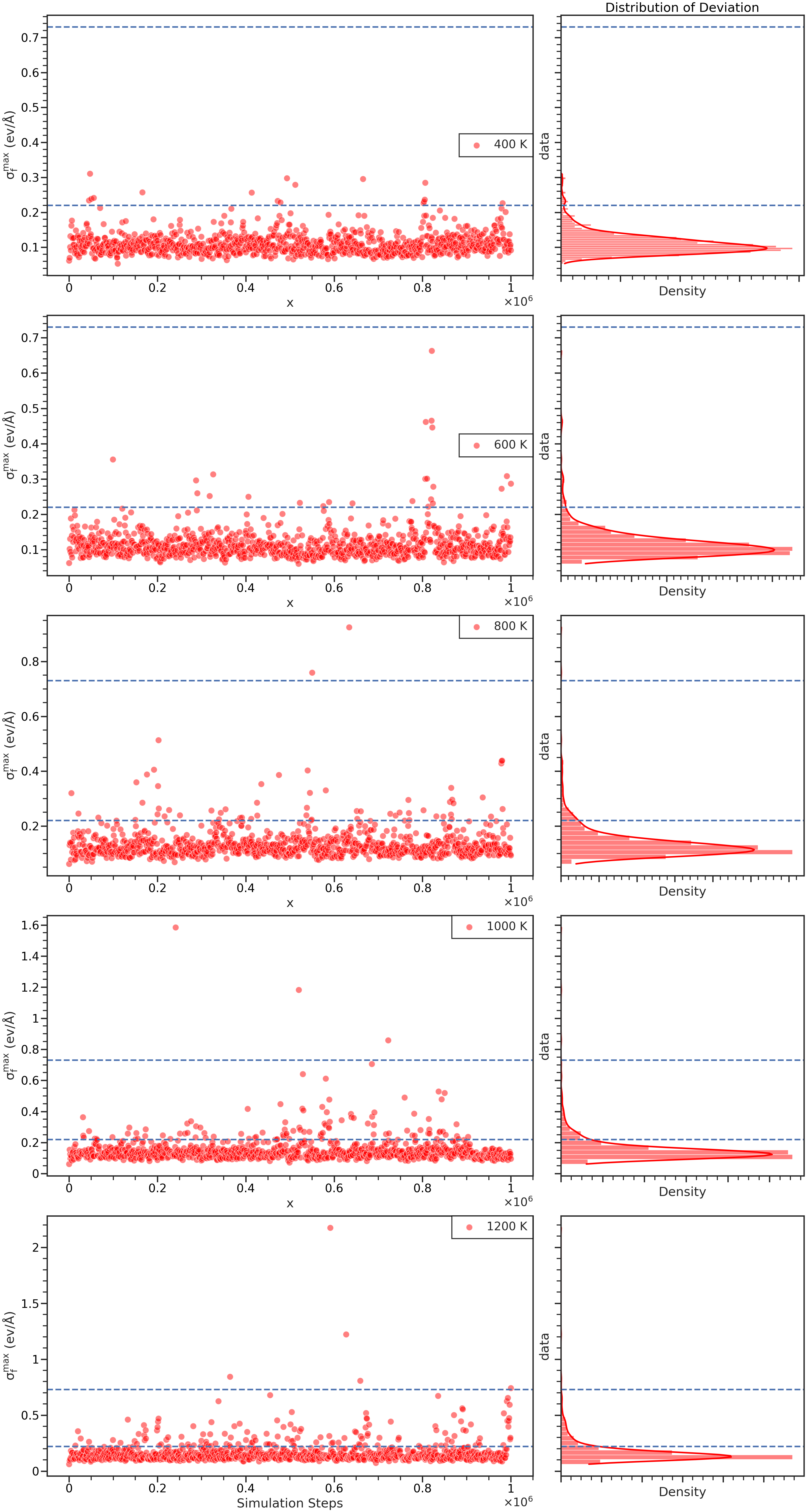
探索（Exploration）

+

类似地，我们也可以对模型的model deviation分布进行分析：

+
from catflow.tesla.dpgen.exploration import DPExplorationAnalyzer
+ana = DPExplorationAnalyzer(t)
+
+

利用分析器自带的方法进行作图：

+
fig = ana.plot_single_iteration(
+    iteration=41, 
+    temps=[400, 600, 800, 1000, 1200],
+    xlimit=1000000,
+    f_trust_lo=t.param_data['model_devi_f_trust_lo'],
+    f_trust_hi=t.param_data['model_devi_f_trust_hi'],
+    style='ticks',
+    group_by='temps',
+    label_unit='K',
+    context='talk'
+)
+
+

其中：

+
    +
  • +

    iteration 对应为所需分析的轮数，默认为最新进行过Exploartion的轮数。

    +
    • +
  • +

    f_trust_lo和f_trust_hi即对应的最大力偏差上下限设置。

    +
    • +
  • +

    通过 group_by 指定所需作图的参数，对应到 param.json 中 model_devi_jobs 中该轮数需要迭代的List，例如：

    +
    • +
+
  {
+      "template": {
+          "lmp": "lmp/input-meta.lammps",
+          "plm": "lmp/input-meta.plumed"
+      },
+      "sys_idx": [
+          53
+      ],
+      "traj_freq": 1000,
+      "rev_mat": {
+          "lmp": {
+              "V_NSTEPS": [
+                  1000000
+              ],
+              "V_TEMP": [
+                  400,
+                  600,
+                  800,
+                  1000,
+                  1200
+              ]
+          }
+      },
+      "model_devi_f_trust_lo": 0.23,
+      "model_devi_f_trust_hi": 0.75
+  }
+
+

若指定group_by 参数为 V_TEMP，则根据该轮的热浴温度分组作图，若指定V_TEMP=[400, 600, 800, 1000, 1200]，则可由400、600、800、1000、1200K分别对model deviation作图。

+
    +
  • label_unit 即 group_by 参数的单位，例如这里是温度，故为"K"。
    • +
+

效果如下：

+

20221110160742

+ + + + + + +
+
+ + +
+ + + +
+ + + +
+
+
+
+ + + + + + + + + + + + + + + + \ No newline at end of file diff --git a/Usage/index.html b/Usage/index.html new file mode 100644 index 0000000..e78b5bc --- /dev/null +++ b/Usage/index.html @@ -0,0 +1,1733 @@ + + + + + + + + + + + + + + + + + + + + + + + + + Usage - catflow + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + Skip to content + + +
+
+ +
+ + + + + + + + +
+ + + + + + + +
+ +
+ + + + +
+
+ + + +
+
+
+ + + + + + + +
+
+
+ + + +
+
+
+ + + +
+
+
+ + + +
+ +
+ + +
+ + + +
+ + + +
+
+
+
+ + + + + + + + + + + + + + + + \ No newline at end of file diff --git a/Usage/metadyn/index.html b/Usage/metadyn/index.html new file mode 100644 index 0000000..cbc0abc --- /dev/null +++ b/Usage/metadyn/index.html @@ -0,0 +1,3372 @@ + + + + + + + + + + + + + + + + + + + + + + + + + Metadynamics 分析 - catflow + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
+ + + + Skip to content + + +
+
+ +
+ + + + + + + + +
+ + + + + + + +
+ +
+ + + + +
+
+ + + +
+
+
+ + + + + + + +
+
+
+ + + +
+
+
+ + + +
+
+
+ + + +
+
+ + + + + + + + + + + + + + + + + + +
+ +
+ + + + + + + + + +
+
+ + +
+ + + +
+ + + +
+
+
+
+ + + + + + + + + + + + + + + + \ No newline at end of file diff --git a/assets/_mkdocstrings.css b/assets/_mkdocstrings.css new file mode 100644 index 0000000..049a254 --- /dev/null +++ b/assets/_mkdocstrings.css @@ -0,0 +1,64 @@ + +/* Avoid breaking parameter names, etc. in table cells. */ +.doc-contents td code { + word-break: normal !important; +} + +/* No line break before first paragraph of descriptions. */ +.doc-md-description, +.doc-md-description>p:first-child { + display: inline; +} + +/* Max width for docstring sections tables. */ +.doc .md-typeset__table, +.doc .md-typeset__table table { + display: table !important; + width: 100%; +} + +.doc .md-typeset__table tr { + display: table-row; +} + +/* Defaults in Spacy table style. */ +.doc-param-default { + float: right; +} + +/* Keep headings consistent. */ +h1.doc-heading, +h2.doc-heading, +h3.doc-heading, +h4.doc-heading, +h5.doc-heading, +h6.doc-heading { + font-weight: 400; + line-height: 1.5; + color: inherit; + text-transform: none; +} + +h1.doc-heading { + font-size: 1.6rem; +} + +h2.doc-heading { + font-size: 1.2rem; +} + +h3.doc-heading { + font-size: 1.15rem; +} + +h4.doc-heading { + font-size: 1.10rem; +} + +h5.doc-heading { + font-size: 1.05rem; +} + +h6.doc-heading { + font-size: 1rem; +} \ No newline at end of file diff --git a/assets/images/favicon.png b/assets/images/favicon.png new file mode 100644 index 0000000..1cf13b9 Binary files /dev/null and b/assets/images/favicon.png differ diff --git a/assets/javascripts/bundle.6c14ae12.min.js b/assets/javascripts/bundle.6c14ae12.min.js new file mode 100644 index 0000000..bbff776 --- /dev/null +++ b/assets/javascripts/bundle.6c14ae12.min.js @@ -0,0 +1,29 @@ +"use strict";(()=>{var wi=Object.create;var ur=Object.defineProperty;var Si=Object.getOwnPropertyDescriptor;var Ti=Object.getOwnPropertyNames,kt=Object.getOwnPropertySymbols,Oi=Object.getPrototypeOf,dr=Object.prototype.hasOwnProperty,Zr=Object.prototype.propertyIsEnumerable;var Xr=(e,t,r)=>t in e?ur(e,t,{enumerable:!0,configurable:!0,writable:!0,value:r}):e[t]=r,R=(e,t)=>{for(var r in t||(t={}))dr.call(t,r)&&Xr(e,r,t[r]);if(kt)for(var r of kt(t))Zr.call(t,r)&&Xr(e,r,t[r]);return e};var eo=(e,t)=>{var r={};for(var o in e)dr.call(e,o)&&t.indexOf(o)<0&&(r[o]=e[o]);if(e!=null&&kt)for(var o of kt(e))t.indexOf(o)<0&&Zr.call(e,o)&&(r[o]=e[o]);return r};var hr=(e,t)=>()=>(t||e((t={exports:{}}).exports,t),t.exports);var Mi=(e,t,r,o)=>{if(t&&typeof t=="object"||typeof t=="function")for(let n of Ti(t))!dr.call(e,n)&&n!==r&&ur(e,n,{get:()=>t[n],enumerable:!(o=Si(t,n))||o.enumerable});return e};var Ht=(e,t,r)=>(r=e!=null?wi(Oi(e)):{},Mi(t||!e||!e.__esModule?ur(r,"default",{value:e,enumerable:!0}):r,e));var ro=hr((br,to)=>{(function(e,t){typeof br=="object"&&typeof to!="undefined"?t():typeof define=="function"&&define.amd?define(t):t()})(br,function(){"use strict";function e(r){var o=!0,n=!1,i=null,s={text:!0,search:!0,url:!0,tel:!0,email:!0,password:!0,number:!0,date:!0,month:!0,week:!0,time:!0,datetime:!0,"datetime-local":!0};function a(C){return!!(C&&C!==document&&C.nodeName!=="HTML"&&C.nodeName!=="BODY"&&"classList"in C&&"contains"in C.classList)}function c(C){var it=C.type,Ue=C.tagName;return!!(Ue==="INPUT"&&s[it]&&!C.readOnly||Ue==="TEXTAREA"&&!C.readOnly||C.isContentEditable)}function p(C){C.classList.contains("focus-visible")||(C.classList.add("focus-visible"),C.setAttribute("data-focus-visible-added",""))}function l(C){C.hasAttribute("data-focus-visible-added")&&(C.classList.remove("focus-visible"),C.removeAttribute("data-focus-visible-added"))}function f(C){C.metaKey||C.altKey||C.ctrlKey||(a(r.activeElement)&&p(r.activeElement),o=!0)}function u(C){o=!1}function d(C){a(C.target)&&(o||c(C.target))&&p(C.target)}function v(C){a(C.target)&&(C.target.classList.contains("focus-visible")||C.target.hasAttribute("data-focus-visible-added"))&&(n=!0,window.clearTimeout(i),i=window.setTimeout(function(){n=!1},100),l(C.target))}function b(C){document.visibilityState==="hidden"&&(n&&(o=!0),z())}function z(){document.addEventListener("mousemove",G),document.addEventListener("mousedown",G),document.addEventListener("mouseup",G),document.addEventListener("pointermove",G),document.addEventListener("pointerdown",G),document.addEventListener("pointerup",G),document.addEventListener("touchmove",G),document.addEventListener("touchstart",G),document.addEventListener("touchend",G)}function K(){document.removeEventListener("mousemove",G),document.removeEventListener("mousedown",G),document.removeEventListener("mouseup",G),document.removeEventListener("pointermove",G),document.removeEventListener("pointerdown",G),document.removeEventListener("pointerup",G),document.removeEventListener("touchmove",G),document.removeEventListener("touchstart",G),document.removeEventListener("touchend",G)}function G(C){C.target.nodeName&&C.target.nodeName.toLowerCase()==="html"||(o=!1,K())}document.addEventListener("keydown",f,!0),document.addEventListener("mousedown",u,!0),document.addEventListener("pointerdown",u,!0),document.addEventListener("touchstart",u,!0),document.addEventListener("visibilitychange",b,!0),z(),r.addEventListener("focus",d,!0),r.addEventListener("blur",v,!0),r.nodeType===Node.DOCUMENT_FRAGMENT_NODE&&r.host?r.host.setAttribute("data-js-focus-visible",""):r.nodeType===Node.DOCUMENT_NODE&&(document.documentElement.classList.add("js-focus-visible"),document.documentElement.setAttribute("data-js-focus-visible",""))}if(typeof window!="undefined"&&typeof document!="undefined"){window.applyFocusVisiblePolyfill=e;var t;try{t=new CustomEvent("focus-visible-polyfill-ready")}catch(r){t=document.createEvent("CustomEvent"),t.initCustomEvent("focus-visible-polyfill-ready",!1,!1,{})}window.dispatchEvent(t)}typeof document!="undefined"&&e(document)})});var Vr=hr((Ot,Dr)=>{/*! + * clipboard.js v2.0.11 + * https://clipboardjs.com/ + * + * Licensed MIT © Zeno Rocha + */(function(t,r){typeof Ot=="object"&&typeof Dr=="object"?Dr.exports=r():typeof define=="function"&&define.amd?define([],r):typeof Ot=="object"?Ot.ClipboardJS=r():t.ClipboardJS=r()})(Ot,function(){return function(){var e={686:function(o,n,i){"use strict";i.d(n,{default:function(){return Ei}});var s=i(279),a=i.n(s),c=i(370),p=i.n(c),l=i(817),f=i.n(l);function u(W){try{return document.execCommand(W)}catch(O){return!1}}var d=function(O){var S=f()(O);return u("cut"),S},v=d;function b(W){var O=document.documentElement.getAttribute("dir")==="rtl",S=document.createElement("textarea");S.style.fontSize="12pt",S.style.border="0",S.style.padding="0",S.style.margin="0",S.style.position="absolute",S.style[O?"right":"left"]="-9999px";var $=window.pageYOffset||document.documentElement.scrollTop;return S.style.top="".concat($,"px"),S.setAttribute("readonly",""),S.value=W,S}var z=function(O,S){var $=b(O);S.container.appendChild($);var F=f()($);return u("copy"),$.remove(),F},K=function(O){var S=arguments.length>1&&arguments[1]!==void 0?arguments[1]:{container:document.body},$="";return typeof O=="string"?$=z(O,S):O instanceof HTMLInputElement&&!["text","search","url","tel","password"].includes(O==null?void 0:O.type)?$=z(O.value,S):($=f()(O),u("copy")),$},G=K;function C(W){"@babel/helpers - typeof";return typeof Symbol=="function"&&typeof Symbol.iterator=="symbol"?C=function(S){return typeof S}:C=function(S){return S&&typeof Symbol=="function"&&S.constructor===Symbol&&S!==Symbol.prototype?"symbol":typeof S},C(W)}var it=function(){var O=arguments.length>0&&arguments[0]!==void 0?arguments[0]:{},S=O.action,$=S===void 0?"copy":S,F=O.container,Q=O.target,_e=O.text;if($!=="copy"&&$!=="cut")throw new Error('Invalid "action" value, use either "copy" or "cut"');if(Q!==void 0)if(Q&&C(Q)==="object"&&Q.nodeType===1){if($==="copy"&&Q.hasAttribute("disabled"))throw new Error('Invalid "target" attribute. Please use "readonly" instead of "disabled" attribute');if($==="cut"&&(Q.hasAttribute("readonly")||Q.hasAttribute("disabled")))throw new Error(`Invalid "target" attribute. You can't cut text from elements with "readonly" or "disabled" attributes`)}else throw new Error('Invalid "target" value, use a valid Element');if(_e)return G(_e,{container:F});if(Q)return $==="cut"?v(Q):G(Q,{container:F})},Ue=it;function Pe(W){"@babel/helpers - typeof";return typeof Symbol=="function"&&typeof Symbol.iterator=="symbol"?Pe=function(S){return typeof S}:Pe=function(S){return S&&typeof Symbol=="function"&&S.constructor===Symbol&&S!==Symbol.prototype?"symbol":typeof S},Pe(W)}function ui(W,O){if(!(W instanceof O))throw new TypeError("Cannot call a class as a function")}function Jr(W,O){for(var S=0;S0&&arguments[0]!==void 0?arguments[0]:{};this.action=typeof F.action=="function"?F.action:this.defaultAction,this.target=typeof F.target=="function"?F.target:this.defaultTarget,this.text=typeof F.text=="function"?F.text:this.defaultText,this.container=Pe(F.container)==="object"?F.container:document.body}},{key:"listenClick",value:function(F){var Q=this;this.listener=p()(F,"click",function(_e){return Q.onClick(_e)})}},{key:"onClick",value:function(F){var Q=F.delegateTarget||F.currentTarget,_e=this.action(Q)||"copy",Ct=Ue({action:_e,container:this.container,target:this.target(Q),text:this.text(Q)});this.emit(Ct?"success":"error",{action:_e,text:Ct,trigger:Q,clearSelection:function(){Q&&Q.focus(),window.getSelection().removeAllRanges()}})}},{key:"defaultAction",value:function(F){return fr("action",F)}},{key:"defaultTarget",value:function(F){var Q=fr("target",F);if(Q)return document.querySelector(Q)}},{key:"defaultText",value:function(F){return fr("text",F)}},{key:"destroy",value:function(){this.listener.destroy()}}],[{key:"copy",value:function(F){var Q=arguments.length>1&&arguments[1]!==void 0?arguments[1]:{container:document.body};return G(F,Q)}},{key:"cut",value:function(F){return v(F)}},{key:"isSupported",value:function(){var F=arguments.length>0&&arguments[0]!==void 0?arguments[0]:["copy","cut"],Q=typeof F=="string"?[F]:F,_e=!!document.queryCommandSupported;return Q.forEach(function(Ct){_e=_e&&!!document.queryCommandSupported(Ct)}),_e}}]),S}(a()),Ei=yi},828:function(o){var n=9;if(typeof Element!="undefined"&&!Element.prototype.matches){var i=Element.prototype;i.matches=i.matchesSelector||i.mozMatchesSelector||i.msMatchesSelector||i.oMatchesSelector||i.webkitMatchesSelector}function s(a,c){for(;a&&a.nodeType!==n;){if(typeof a.matches=="function"&&a.matches(c))return a;a=a.parentNode}}o.exports=s},438:function(o,n,i){var s=i(828);function a(l,f,u,d,v){var b=p.apply(this,arguments);return l.addEventListener(u,b,v),{destroy:function(){l.removeEventListener(u,b,v)}}}function c(l,f,u,d,v){return typeof l.addEventListener=="function"?a.apply(null,arguments):typeof u=="function"?a.bind(null,document).apply(null,arguments):(typeof l=="string"&&(l=document.querySelectorAll(l)),Array.prototype.map.call(l,function(b){return a(b,f,u,d,v)}))}function p(l,f,u,d){return function(v){v.delegateTarget=s(v.target,f),v.delegateTarget&&d.call(l,v)}}o.exports=c},879:function(o,n){n.node=function(i){return i!==void 0&&i instanceof HTMLElement&&i.nodeType===1},n.nodeList=function(i){var s=Object.prototype.toString.call(i);return i!==void 0&&(s==="[object NodeList]"||s==="[object HTMLCollection]")&&"length"in i&&(i.length===0||n.node(i[0]))},n.string=function(i){return typeof i=="string"||i instanceof String},n.fn=function(i){var s=Object.prototype.toString.call(i);return s==="[object Function]"}},370:function(o,n,i){var s=i(879),a=i(438);function c(u,d,v){if(!u&&!d&&!v)throw new Error("Missing required arguments");if(!s.string(d))throw new TypeError("Second argument must be a String");if(!s.fn(v))throw new TypeError("Third argument must be a Function");if(s.node(u))return p(u,d,v);if(s.nodeList(u))return l(u,d,v);if(s.string(u))return f(u,d,v);throw new TypeError("First argument must be a String, HTMLElement, HTMLCollection, or NodeList")}function p(u,d,v){return u.addEventListener(d,v),{destroy:function(){u.removeEventListener(d,v)}}}function l(u,d,v){return Array.prototype.forEach.call(u,function(b){b.addEventListener(d,v)}),{destroy:function(){Array.prototype.forEach.call(u,function(b){b.removeEventListener(d,v)})}}}function f(u,d,v){return a(document.body,u,d,v)}o.exports=c},817:function(o){function n(i){var s;if(i.nodeName==="SELECT")i.focus(),s=i.value;else if(i.nodeName==="INPUT"||i.nodeName==="TEXTAREA"){var a=i.hasAttribute("readonly");a||i.setAttribute("readonly",""),i.select(),i.setSelectionRange(0,i.value.length),a||i.removeAttribute("readonly"),s=i.value}else{i.hasAttribute("contenteditable")&&i.focus();var c=window.getSelection(),p=document.createRange();p.selectNodeContents(i),c.removeAllRanges(),c.addRange(p),s=c.toString()}return s}o.exports=n},279:function(o){function n(){}n.prototype={on:function(i,s,a){var c=this.e||(this.e={});return(c[i]||(c[i]=[])).push({fn:s,ctx:a}),this},once:function(i,s,a){var c=this;function p(){c.off(i,p),s.apply(a,arguments)}return p._=s,this.on(i,p,a)},emit:function(i){var s=[].slice.call(arguments,1),a=((this.e||(this.e={}))[i]||[]).slice(),c=0,p=a.length;for(c;c{"use strict";/*! + * escape-html + * Copyright(c) 2012-2013 TJ Holowaychuk + * Copyright(c) 2015 Andreas Lubbe + * Copyright(c) 2015 Tiancheng "Timothy" Gu + * MIT Licensed + */var Ha=/["'&<>]/;Nn.exports=$a;function $a(e){var t=""+e,r=Ha.exec(t);if(!r)return t;var o,n="",i=0,s=0;for(i=r.index;i0&&i[i.length-1])&&(p[0]===6||p[0]===2)){r=0;continue}if(p[0]===3&&(!i||p[1]>i[0]&&p[1]=e.length&&(e=void 0),{value:e&&e[o++],done:!e}}};throw new TypeError(t?"Object is not iterable.":"Symbol.iterator is not defined.")}function N(e,t){var r=typeof Symbol=="function"&&e[Symbol.iterator];if(!r)return e;var o=r.call(e),n,i=[],s;try{for(;(t===void 0||t-- >0)&&!(n=o.next()).done;)i.push(n.value)}catch(a){s={error:a}}finally{try{n&&!n.done&&(r=o.return)&&r.call(o)}finally{if(s)throw s.error}}return i}function D(e,t,r){if(r||arguments.length===2)for(var o=0,n=t.length,i;o1||a(u,d)})})}function a(u,d){try{c(o[u](d))}catch(v){f(i[0][3],v)}}function c(u){u.value instanceof Ze?Promise.resolve(u.value.v).then(p,l):f(i[0][2],u)}function p(u){a("next",u)}function l(u){a("throw",u)}function f(u,d){u(d),i.shift(),i.length&&a(i[0][0],i[0][1])}}function io(e){if(!Symbol.asyncIterator)throw new TypeError("Symbol.asyncIterator is not defined.");var t=e[Symbol.asyncIterator],r;return t?t.call(e):(e=typeof we=="function"?we(e):e[Symbol.iterator](),r={},o("next"),o("throw"),o("return"),r[Symbol.asyncIterator]=function(){return this},r);function o(i){r[i]=e[i]&&function(s){return new Promise(function(a,c){s=e[i](s),n(a,c,s.done,s.value)})}}function n(i,s,a,c){Promise.resolve(c).then(function(p){i({value:p,done:a})},s)}}function k(e){return typeof e=="function"}function at(e){var t=function(o){Error.call(o),o.stack=new Error().stack},r=e(t);return r.prototype=Object.create(Error.prototype),r.prototype.constructor=r,r}var Rt=at(function(e){return function(r){e(this),this.message=r?r.length+` errors occurred during unsubscription: +`+r.map(function(o,n){return n+1+") "+o.toString()}).join(` + `):"",this.name="UnsubscriptionError",this.errors=r}});function De(e,t){if(e){var r=e.indexOf(t);0<=r&&e.splice(r,1)}}var Ie=function(){function e(t){this.initialTeardown=t,this.closed=!1,this._parentage=null,this._finalizers=null}return e.prototype.unsubscribe=function(){var t,r,o,n,i;if(!this.closed){this.closed=!0;var s=this._parentage;if(s)if(this._parentage=null,Array.isArray(s))try{for(var a=we(s),c=a.next();!c.done;c=a.next()){var p=c.value;p.remove(this)}}catch(b){t={error:b}}finally{try{c&&!c.done&&(r=a.return)&&r.call(a)}finally{if(t)throw t.error}}else s.remove(this);var l=this.initialTeardown;if(k(l))try{l()}catch(b){i=b instanceof Rt?b.errors:[b]}var f=this._finalizers;if(f){this._finalizers=null;try{for(var u=we(f),d=u.next();!d.done;d=u.next()){var v=d.value;try{ao(v)}catch(b){i=i!=null?i:[],b instanceof Rt?i=D(D([],N(i)),N(b.errors)):i.push(b)}}}catch(b){o={error:b}}finally{try{d&&!d.done&&(n=u.return)&&n.call(u)}finally{if(o)throw o.error}}}if(i)throw new Rt(i)}},e.prototype.add=function(t){var r;if(t&&t!==this)if(this.closed)ao(t);else{if(t instanceof e){if(t.closed||t._hasParent(this))return;t._addParent(this)}(this._finalizers=(r=this._finalizers)!==null&&r!==void 0?r:[]).push(t)}},e.prototype._hasParent=function(t){var r=this._parentage;return r===t||Array.isArray(r)&&r.includes(t)},e.prototype._addParent=function(t){var r=this._parentage;this._parentage=Array.isArray(r)?(r.push(t),r):r?[r,t]:t},e.prototype._removeParent=function(t){var r=this._parentage;r===t?this._parentage=null:Array.isArray(r)&&De(r,t)},e.prototype.remove=function(t){var r=this._finalizers;r&&De(r,t),t instanceof e&&t._removeParent(this)},e.EMPTY=function(){var t=new e;return t.closed=!0,t}(),e}();var gr=Ie.EMPTY;function Pt(e){return e instanceof Ie||e&&"closed"in e&&k(e.remove)&&k(e.add)&&k(e.unsubscribe)}function ao(e){k(e)?e():e.unsubscribe()}var Ae={onUnhandledError:null,onStoppedNotification:null,Promise:void 0,useDeprecatedSynchronousErrorHandling:!1,useDeprecatedNextContext:!1};var st={setTimeout:function(e,t){for(var r=[],o=2;o0},enumerable:!1,configurable:!0}),t.prototype._trySubscribe=function(r){return this._throwIfClosed(),e.prototype._trySubscribe.call(this,r)},t.prototype._subscribe=function(r){return this._throwIfClosed(),this._checkFinalizedStatuses(r),this._innerSubscribe(r)},t.prototype._innerSubscribe=function(r){var o=this,n=this,i=n.hasError,s=n.isStopped,a=n.observers;return i||s?gr:(this.currentObservers=null,a.push(r),new Ie(function(){o.currentObservers=null,De(a,r)}))},t.prototype._checkFinalizedStatuses=function(r){var o=this,n=o.hasError,i=o.thrownError,s=o.isStopped;n?r.error(i):s&&r.complete()},t.prototype.asObservable=function(){var r=new P;return r.source=this,r},t.create=function(r,o){return new ho(r,o)},t}(P);var ho=function(e){ie(t,e);function t(r,o){var n=e.call(this)||this;return n.destination=r,n.source=o,n}return t.prototype.next=function(r){var o,n;(n=(o=this.destination)===null||o===void 0?void 0:o.next)===null||n===void 0||n.call(o,r)},t.prototype.error=function(r){var o,n;(n=(o=this.destination)===null||o===void 0?void 0:o.error)===null||n===void 0||n.call(o,r)},t.prototype.complete=function(){var r,o;(o=(r=this.destination)===null||r===void 0?void 0:r.complete)===null||o===void 0||o.call(r)},t.prototype._subscribe=function(r){var o,n;return(n=(o=this.source)===null||o===void 0?void 0:o.subscribe(r))!==null&&n!==void 0?n:gr},t}(x);var yt={now:function(){return(yt.delegate||Date).now()},delegate:void 0};var Et=function(e){ie(t,e);function t(r,o,n){r===void 0&&(r=1/0),o===void 0&&(o=1/0),n===void 0&&(n=yt);var i=e.call(this)||this;return i._bufferSize=r,i._windowTime=o,i._timestampProvider=n,i._buffer=[],i._infiniteTimeWindow=!0,i._infiniteTimeWindow=o===1/0,i._bufferSize=Math.max(1,r),i._windowTime=Math.max(1,o),i}return t.prototype.next=function(r){var o=this,n=o.isStopped,i=o._buffer,s=o._infiniteTimeWindow,a=o._timestampProvider,c=o._windowTime;n||(i.push(r),!s&&i.push(a.now()+c)),this._trimBuffer(),e.prototype.next.call(this,r)},t.prototype._subscribe=function(r){this._throwIfClosed(),this._trimBuffer();for(var o=this._innerSubscribe(r),n=this,i=n._infiniteTimeWindow,s=n._buffer,a=s.slice(),c=0;c0?e.prototype.requestAsyncId.call(this,r,o,n):(r.actions.push(this),r._scheduled||(r._scheduled=lt.requestAnimationFrame(function(){return r.flush(void 0)})))},t.prototype.recycleAsyncId=function(r,o,n){var i;if(n===void 0&&(n=0),n!=null?n>0:this.delay>0)return e.prototype.recycleAsyncId.call(this,r,o,n);var s=r.actions;o!=null&&((i=s[s.length-1])===null||i===void 0?void 0:i.id)!==o&&(lt.cancelAnimationFrame(o),r._scheduled=void 0)},t}(jt);var go=function(e){ie(t,e);function t(){return e!==null&&e.apply(this,arguments)||this}return t.prototype.flush=function(r){this._active=!0;var o=this._scheduled;this._scheduled=void 0;var n=this.actions,i;r=r||n.shift();do if(i=r.execute(r.state,r.delay))break;while((r=n[0])&&r.id===o&&n.shift());if(this._active=!1,i){for(;(r=n[0])&&r.id===o&&n.shift();)r.unsubscribe();throw i}},t}(Wt);var Oe=new go(vo);var L=new P(function(e){return e.complete()});function Nt(e){return e&&k(e.schedule)}function Or(e){return e[e.length-1]}function Qe(e){return k(Or(e))?e.pop():void 0}function Me(e){return Nt(Or(e))?e.pop():void 0}function Ut(e,t){return typeof Or(e)=="number"?e.pop():t}var mt=function(e){return e&&typeof e.length=="number"&&typeof e!="function"};function Dt(e){return k(e==null?void 0:e.then)}function Vt(e){return k(e[pt])}function zt(e){return Symbol.asyncIterator&&k(e==null?void 0:e[Symbol.asyncIterator])}function qt(e){return new TypeError("You provided "+(e!==null&&typeof e=="object"?"an invalid object":"'"+e+"'")+" where a stream was expected. You can provide an Observable, Promise, ReadableStream, Array, AsyncIterable, or Iterable.")}function Pi(){return typeof Symbol!="function"||!Symbol.iterator?"@@iterator":Symbol.iterator}var Kt=Pi();function Qt(e){return k(e==null?void 0:e[Kt])}function Yt(e){return no(this,arguments,function(){var r,o,n,i;return $t(this,function(s){switch(s.label){case 0:r=e.getReader(),s.label=1;case 1:s.trys.push([1,,9,10]),s.label=2;case 2:return[4,Ze(r.read())];case 3:return o=s.sent(),n=o.value,i=o.done,i?[4,Ze(void 0)]:[3,5];case 4:return[2,s.sent()];case 5:return[4,Ze(n)];case 6:return[4,s.sent()];case 7:return s.sent(),[3,2];case 8:return[3,10];case 9:return r.releaseLock(),[7];case 10:return[2]}})})}function Bt(e){return k(e==null?void 0:e.getReader)}function I(e){if(e instanceof P)return e;if(e!=null){if(Vt(e))return Ii(e);if(mt(e))return Fi(e);if(Dt(e))return ji(e);if(zt(e))return xo(e);if(Qt(e))return Wi(e);if(Bt(e))return Ni(e)}throw qt(e)}function Ii(e){return new P(function(t){var r=e[pt]();if(k(r.subscribe))return r.subscribe(t);throw new TypeError("Provided object does not correctly implement Symbol.observable")})}function Fi(e){return new P(function(t){for(var r=0;r=2;return function(o){return o.pipe(e?M(function(n,i){return e(n,i,o)}):ue,xe(1),r?He(t):Io(function(){return new Jt}))}}function Fo(){for(var e=[],t=0;t=2,!0))}function le(e){e===void 0&&(e={});var t=e.connector,r=t===void 0?function(){return new x}:t,o=e.resetOnError,n=o===void 0?!0:o,i=e.resetOnComplete,s=i===void 0?!0:i,a=e.resetOnRefCountZero,c=a===void 0?!0:a;return function(p){var l,f,u,d=0,v=!1,b=!1,z=function(){f==null||f.unsubscribe(),f=void 0},K=function(){z(),l=u=void 0,v=b=!1},G=function(){var C=l;K(),C==null||C.unsubscribe()};return g(function(C,it){d++,!b&&!v&&z();var Ue=u=u!=null?u:r();it.add(function(){d--,d===0&&!b&&!v&&(f=Hr(G,c))}),Ue.subscribe(it),!l&&d>0&&(l=new tt({next:function(Pe){return Ue.next(Pe)},error:function(Pe){b=!0,z(),f=Hr(K,n,Pe),Ue.error(Pe)},complete:function(){v=!0,z(),f=Hr(K,s),Ue.complete()}}),I(C).subscribe(l))})(p)}}function Hr(e,t){for(var r=[],o=2;oe.next(document)),e}function q(e,t=document){return Array.from(t.querySelectorAll(e))}function U(e,t=document){let r=se(e,t);if(typeof r=="undefined")throw new ReferenceError(`Missing element: expected "${e}" to be present`);return r}function se(e,t=document){return t.querySelector(e)||void 0}function Re(){return document.activeElement instanceof HTMLElement&&document.activeElement||void 0}var na=_(h(document.body,"focusin"),h(document.body,"focusout")).pipe(ke(1),V(void 0),m(()=>Re()||document.body),J(1));function Zt(e){return na.pipe(m(t=>e.contains(t)),X())}function Je(e){return{x:e.offsetLeft,y:e.offsetTop}}function Uo(e){return _(h(window,"load"),h(window,"resize")).pipe(Ce(0,Oe),m(()=>Je(e)),V(Je(e)))}function er(e){return{x:e.scrollLeft,y:e.scrollTop}}function dt(e){return _(h(e,"scroll"),h(window,"resize")).pipe(Ce(0,Oe),m(()=>er(e)),V(er(e)))}function Do(e,t){if(typeof t=="string"||typeof t=="number")e.innerHTML+=t.toString();else if(t instanceof Node)e.appendChild(t);else if(Array.isArray(t))for(let r of t)Do(e,r)}function T(e,t,...r){let o=document.createElement(e);if(t)for(let n of Object.keys(t))typeof t[n]!="undefined"&&(typeof t[n]!="boolean"?o.setAttribute(n,t[n]):o.setAttribute(n,""));for(let n of r)Do(o,n);return o}function tr(e){if(e>999){let t=+((e-950)%1e3>99);return`${((e+1e-6)/1e3).toFixed(t)}k`}else return e.toString()}function ht(e){let t=T("script",{src:e});return H(()=>(document.head.appendChild(t),_(h(t,"load"),h(t,"error").pipe(E(()=>Mr(()=>new ReferenceError(`Invalid script: ${e}`))))).pipe(m(()=>{}),A(()=>document.head.removeChild(t)),xe(1))))}var Vo=new x,ia=H(()=>typeof ResizeObserver=="undefined"?ht("https://unpkg.com/resize-observer-polyfill"):j(void 0)).pipe(m(()=>new ResizeObserver(e=>{for(let t of e)Vo.next(t)})),E(e=>_(Ve,j(e)).pipe(A(()=>e.disconnect()))),J(1));function he(e){return{width:e.offsetWidth,height:e.offsetHeight}}function ye(e){return ia.pipe(w(t=>t.observe(e)),E(t=>Vo.pipe(M(({target:r})=>r===e),A(()=>t.unobserve(e)),m(()=>he(e)))),V(he(e)))}function bt(e){return{width:e.scrollWidth,height:e.scrollHeight}}function zo(e){let t=e.parentElement;for(;t&&(e.scrollWidth<=t.scrollWidth&&e.scrollHeight<=t.scrollHeight);)t=(e=t).parentElement;return t?e:void 0}var qo=new x,aa=H(()=>j(new IntersectionObserver(e=>{for(let t of e)qo.next(t)},{threshold:0}))).pipe(E(e=>_(Ve,j(e)).pipe(A(()=>e.disconnect()))),J(1));function rr(e){return aa.pipe(w(t=>t.observe(e)),E(t=>qo.pipe(M(({target:r})=>r===e),A(()=>t.unobserve(e)),m(({isIntersecting:r})=>r))))}function Ko(e,t=16){return dt(e).pipe(m(({y:r})=>{let o=he(e),n=bt(e);return r>=n.height-o.height-t}),X())}var or={drawer:U("[data-md-toggle=drawer]"),search:U("[data-md-toggle=search]")};function Qo(e){return or[e].checked}function Ke(e,t){or[e].checked!==t&&or[e].click()}function We(e){let t=or[e];return h(t,"change").pipe(m(()=>t.checked),V(t.checked))}function sa(e,t){switch(e.constructor){case HTMLInputElement:return e.type==="radio"?/^Arrow/.test(t):!0;case HTMLSelectElement:case HTMLTextAreaElement:return!0;default:return e.isContentEditable}}function ca(){return _(h(window,"compositionstart").pipe(m(()=>!0)),h(window,"compositionend").pipe(m(()=>!1))).pipe(V(!1))}function Yo(){let e=h(window,"keydown").pipe(M(t=>!(t.metaKey||t.ctrlKey)),m(t=>({mode:Qo("search")?"search":"global",type:t.key,claim(){t.preventDefault(),t.stopPropagation()}})),M(({mode:t,type:r})=>{if(t==="global"){let o=Re();if(typeof o!="undefined")return!sa(o,r)}return!0}),le());return ca().pipe(E(t=>t?L:e))}function pe(){return new URL(location.href)}function ot(e,t=!1){if(te("navigation.instant")&&!t){let r=T("a",{href:e.href});document.body.appendChild(r),r.click(),r.remove()}else location.href=e.href}function Bo(){return new x}function Go(){return location.hash.slice(1)}function nr(e){let t=T("a",{href:e});t.addEventListener("click",r=>r.stopPropagation()),t.click()}function pa(e){return _(h(window,"hashchange"),e).pipe(m(Go),V(Go()),M(t=>t.length>0),J(1))}function Jo(e){return pa(e).pipe(m(t=>se(`[id="${t}"]`)),M(t=>typeof t!="undefined"))}function Fr(e){let t=matchMedia(e);return Xt(r=>t.addListener(()=>r(t.matches))).pipe(V(t.matches))}function Xo(){let e=matchMedia("print");return _(h(window,"beforeprint").pipe(m(()=>!0)),h(window,"afterprint").pipe(m(()=>!1))).pipe(V(e.matches))}function jr(e,t){return e.pipe(E(r=>r?t():L))}function ir(e,t){return new P(r=>{let o=new XMLHttpRequest;o.open("GET",`${e}`),o.responseType="blob",o.addEventListener("load",()=>{o.status>=200&&o.status<300?(r.next(o.response),r.complete()):r.error(new Error(o.statusText))}),o.addEventListener("error",()=>{r.error(new Error("Network Error"))}),o.addEventListener("abort",()=>{r.error(new Error("Request aborted"))}),typeof(t==null?void 0:t.progress$)!="undefined"&&(o.addEventListener("progress",n=>{if(n.lengthComputable)t.progress$.next(n.loaded/n.total*100);else{let i=Number(o.getResponseHeader("Content-Length"))||0;t.progress$.next(n.loaded/i*100)}}),t.progress$.next(5)),o.send()})}function Ne(e,t){return ir(e,t).pipe(E(r=>r.text()),m(r=>JSON.parse(r)),J(1))}function Zo(e,t){let r=new DOMParser;return ir(e,t).pipe(E(o=>o.text()),m(o=>r.parseFromString(o,"text/xml")),J(1))}function en(){return{x:Math.max(0,scrollX),y:Math.max(0,scrollY)}}function tn(){return _(h(window,"scroll",{passive:!0}),h(window,"resize",{passive:!0})).pipe(m(en),V(en()))}function rn(){return{width:innerWidth,height:innerHeight}}function on(){return h(window,"resize",{passive:!0}).pipe(m(rn),V(rn()))}function nn(){return B([tn(),on()]).pipe(m(([e,t])=>({offset:e,size:t})),J(1))}function ar(e,{viewport$:t,header$:r}){let o=t.pipe(ee("size")),n=B([o,r]).pipe(m(()=>Je(e)));return B([r,t,n]).pipe(m(([{height:i},{offset:s,size:a},{x:c,y:p}])=>({offset:{x:s.x-c,y:s.y-p+i},size:a})))}function la(e){return h(e,"message",t=>t.data)}function ma(e){let t=new x;return t.subscribe(r=>e.postMessage(r)),t}function an(e,t=new Worker(e)){let r=la(t),o=ma(t),n=new x;n.subscribe(o);let i=o.pipe(Z(),re(!0));return n.pipe(Z(),qe(r.pipe(Y(i))),le())}var fa=U("#__config"),vt=JSON.parse(fa.textContent);vt.base=`${new URL(vt.base,pe())}`;function me(){return vt}function te(e){return vt.features.includes(e)}function be(e,t){return typeof t!="undefined"?vt.translations[e].replace("#",t.toString()):vt.translations[e]}function Ee(e,t=document){return U(`[data-md-component=${e}]`,t)}function oe(e,t=document){return q(`[data-md-component=${e}]`,t)}function ua(e){let t=U(".md-typeset > :first-child",e);return h(t,"click",{once:!0}).pipe(m(()=>U(".md-typeset",e)),m(r=>({hash:__md_hash(r.innerHTML)})))}function sn(e){if(!te("announce.dismiss")||!e.childElementCount)return L;if(!e.hidden){let t=U(".md-typeset",e);__md_hash(t.innerHTML)===__md_get("__announce")&&(e.hidden=!0)}return H(()=>{let t=new x;return t.subscribe(({hash:r})=>{e.hidden=!0,__md_set("__announce",r)}),ua(e).pipe(w(r=>t.next(r)),A(()=>t.complete()),m(r=>R({ref:e},r)))})}function da(e,{target$:t}){return t.pipe(m(r=>({hidden:r!==e})))}function cn(e,t){let r=new x;return r.subscribe(({hidden:o})=>{e.hidden=o}),da(e,t).pipe(w(o=>r.next(o)),A(()=>r.complete()),m(o=>R({ref:e},o)))}function ha(e,t){let r=H(()=>B([Uo(e),dt(t)])).pipe(m(([{x:o,y:n},i])=>{let{width:s,height:a}=he(e);return{x:o-i.x+s/2,y:n-i.y+a/2}}));return Zt(e).pipe(E(o=>r.pipe(m(n=>({active:o,offset:n})),xe(+!o||1/0))))}function pn(e,t,{target$:r}){let[o,n]=Array.from(e.children);return H(()=>{let i=new x,s=i.pipe(Z(),re(!0));return i.subscribe({next({offset:a}){e.style.setProperty("--md-tooltip-x",`${a.x}px`),e.style.setProperty("--md-tooltip-y",`${a.y}px`)},complete(){e.style.removeProperty("--md-tooltip-x"),e.style.removeProperty("--md-tooltip-y")}}),rr(e).pipe(Y(s)).subscribe(a=>{e.toggleAttribute("data-md-visible",a)}),_(i.pipe(M(({active:a})=>a)),i.pipe(ke(250),M(({active:a})=>!a))).subscribe({next({active:a}){a?e.prepend(o):o.remove()},complete(){e.prepend(o)}}),i.pipe(Ce(16,Oe)).subscribe(({active:a})=>{o.classList.toggle("md-tooltip--active",a)}),i.pipe(Pr(125,Oe),M(()=>!!e.offsetParent),m(()=>e.offsetParent.getBoundingClientRect()),m(({x:a})=>a)).subscribe({next(a){a?e.style.setProperty("--md-tooltip-0",`${-a}px`):e.style.removeProperty("--md-tooltip-0")},complete(){e.style.removeProperty("--md-tooltip-0")}}),h(n,"click").pipe(Y(s),M(a=>!(a.metaKey||a.ctrlKey))).subscribe(a=>{a.stopPropagation(),a.preventDefault()}),h(n,"mousedown").pipe(Y(s),ne(i)).subscribe(([a,{active:c}])=>{var p;if(a.button!==0||a.metaKey||a.ctrlKey)a.preventDefault();else if(c){a.preventDefault();let l=e.parentElement.closest(".md-annotation");l instanceof HTMLElement?l.focus():(p=Re())==null||p.blur()}}),r.pipe(Y(s),M(a=>a===o),ze(125)).subscribe(()=>e.focus()),ha(e,t).pipe(w(a=>i.next(a)),A(()=>i.complete()),m(a=>R({ref:e},a)))})}function Wr(e){return T("div",{class:"md-tooltip",id:e},T("div",{class:"md-tooltip__inner md-typeset"}))}function ln(e,t){if(t=t?`${t}_annotation_${e}`:void 0,t){let r=t?`#${t}`:void 0;return T("aside",{class:"md-annotation",tabIndex:0},Wr(t),T("a",{href:r,class:"md-annotation__index",tabIndex:-1},T("span",{"data-md-annotation-id":e})))}else return T("aside",{class:"md-annotation",tabIndex:0},Wr(t),T("span",{class:"md-annotation__index",tabIndex:-1},T("span",{"data-md-annotation-id":e})))}function mn(e){return T("button",{class:"md-clipboard md-icon",title:be("clipboard.copy"),"data-clipboard-target":`#${e} > code`})}function Nr(e,t){let r=t&2,o=t&1,n=Object.keys(e.terms).filter(c=>!e.terms[c]).reduce((c,p)=>[...c,T("del",null,p)," "],[]).slice(0,-1),i=me(),s=new URL(e.location,i.base);te("search.highlight")&&s.searchParams.set("h",Object.entries(e.terms).filter(([,c])=>c).reduce((c,[p])=>`${c} ${p}`.trim(),""));let{tags:a}=me();return T("a",{href:`${s}`,class:"md-search-result__link",tabIndex:-1},T("article",{class:"md-search-result__article md-typeset","data-md-score":e.score.toFixed(2)},r>0&&T("div",{class:"md-search-result__icon md-icon"}),r>0&&T("h1",null,e.title),r<=0&&T("h2",null,e.title),o>0&&e.text.length>0&&e.text,e.tags&&e.tags.map(c=>{let p=a?c in a?`md-tag-icon md-tag--${a[c]}`:"md-tag-icon":"";return T("span",{class:`md-tag ${p}`},c)}),o>0&&n.length>0&&T("p",{class:"md-search-result__terms"},be("search.result.term.missing"),": ",...n)))}function fn(e){let t=e[0].score,r=[...e],o=me(),n=r.findIndex(l=>!`${new URL(l.location,o.base)}`.includes("#")),[i]=r.splice(n,1),s=r.findIndex(l=>l.scoreNr(l,1)),...c.length?[T("details",{class:"md-search-result__more"},T("summary",{tabIndex:-1},T("div",null,c.length>0&&c.length===1?be("search.result.more.one"):be("search.result.more.other",c.length))),...c.map(l=>Nr(l,1)))]:[]];return T("li",{class:"md-search-result__item"},p)}function un(e){return T("ul",{class:"md-source__facts"},Object.entries(e).map(([t,r])=>T("li",{class:`md-source__fact md-source__fact--${t}`},typeof r=="number"?tr(r):r)))}function Ur(e){let t=`tabbed-control tabbed-control--${e}`;return T("div",{class:t,hidden:!0},T("button",{class:"tabbed-button",tabIndex:-1,"aria-hidden":"true"}))}function dn(e){return T("div",{class:"md-typeset__scrollwrap"},T("div",{class:"md-typeset__table"},e))}function ba(e){let t=me(),r=new URL(`../${e.version}/`,t.base);return T("li",{class:"md-version__item"},T("a",{href:`${r}`,class:"md-version__link"},e.title))}function hn(e,t){return T("div",{class:"md-version"},T("button",{class:"md-version__current","aria-label":be("select.version")},t.title),T("ul",{class:"md-version__list"},e.map(ba)))}function va(e){return e.tagName==="CODE"?q(".c, .c1, .cm",e):[e]}function ga(e){let t=[];for(let r of va(e)){let o=[],n=document.createNodeIterator(r,NodeFilter.SHOW_TEXT);for(let i=n.nextNode();i;i=n.nextNode())o.push(i);for(let i of o){let s;for(;s=/(\(\d+\))(!)?/.exec(i.textContent);){let[,a,c]=s;if(typeof c=="undefined"){let p=i.splitText(s.index);i=p.splitText(a.length),t.push(p)}else{i.textContent=a,t.push(i);break}}}}return t}function bn(e,t){t.append(...Array.from(e.childNodes))}function sr(e,t,{target$:r,print$:o}){let n=t.closest("[id]"),i=n==null?void 0:n.id,s=new Map;for(let a of ga(t)){let[,c]=a.textContent.match(/\((\d+)\)/);se(`:scope > li:nth-child(${c})`,e)&&(s.set(c,ln(c,i)),a.replaceWith(s.get(c)))}return s.size===0?L:H(()=>{let a=new x,c=a.pipe(Z(),re(!0)),p=[];for(let[l,f]of s)p.push([U(".md-typeset",f),U(`:scope > li:nth-child(${l})`,e)]);return o.pipe(Y(c)).subscribe(l=>{e.hidden=!l,e.classList.toggle("md-annotation-list",l);for(let[f,u]of p)l?bn(f,u):bn(u,f)}),_(...[...s].map(([,l])=>pn(l,t,{target$:r}))).pipe(A(()=>a.complete()),le())})}function vn(e){if(e.nextElementSibling){let t=e.nextElementSibling;if(t.tagName==="OL")return t;if(t.tagName==="P"&&!t.children.length)return vn(t)}}function gn(e,t){return H(()=>{let r=vn(e);return typeof r!="undefined"?sr(r,e,t):L})}var yn=Ht(Vr());var xa=0;function En(e){if(e.nextElementSibling){let t=e.nextElementSibling;if(t.tagName==="OL")return t;if(t.tagName==="P"&&!t.children.length)return En(t)}}function xn(e){return ye(e).pipe(m(({width:t})=>({scrollable:bt(e).width>t})),ee("scrollable"))}function wn(e,t){let{matches:r}=matchMedia("(hover)"),o=H(()=>{let n=new x;if(n.subscribe(({scrollable:s})=>{s&&r?e.setAttribute("tabindex","0"):e.removeAttribute("tabindex")}),yn.default.isSupported()&&(e.closest(".copy")||te("content.code.copy")&&!e.closest(".no-copy"))){let s=e.closest("pre");s.id=`__code_${xa++}`,s.insertBefore(mn(s.id),e)}let i=e.closest(".highlight");if(i instanceof HTMLElement){let s=En(i);if(typeof s!="undefined"&&(i.classList.contains("annotate")||te("content.code.annotate"))){let a=sr(s,e,t);return xn(e).pipe(w(c=>n.next(c)),A(()=>n.complete()),m(c=>R({ref:e},c)),qe(ye(i).pipe(m(({width:c,height:p})=>c&&p),X(),E(c=>c?a:L))))}}return xn(e).pipe(w(s=>n.next(s)),A(()=>n.complete()),m(s=>R({ref:e},s)))});return te("content.lazy")?rr(e).pipe(M(n=>n),xe(1),E(()=>o)):o}function ya(e,{target$:t,print$:r}){let o=!0;return _(t.pipe(m(n=>n.closest("details:not([open])")),M(n=>e===n),m(()=>({action:"open",reveal:!0}))),r.pipe(M(n=>n||!o),w(()=>o=e.open),m(n=>({action:n?"open":"close"}))))}function Sn(e,t){return H(()=>{let r=new x;return r.subscribe(({action:o,reveal:n})=>{e.toggleAttribute("open",o==="open"),n&&e.scrollIntoView()}),ya(e,t).pipe(w(o=>r.next(o)),A(()=>r.complete()),m(o=>R({ref:e},o)))})}var Tn=".node circle,.node ellipse,.node path,.node polygon,.node rect{fill:var(--md-mermaid-node-bg-color);stroke:var(--md-mermaid-node-fg-color)}marker{fill:var(--md-mermaid-edge-color)!important}.edgeLabel .label rect{fill:#0000}.label{color:var(--md-mermaid-label-fg-color);font-family:var(--md-mermaid-font-family)}.label foreignObject{line-height:normal;overflow:visible}.label div .edgeLabel{color:var(--md-mermaid-label-fg-color)}.edgeLabel,.edgeLabel rect,.label div .edgeLabel{background-color:var(--md-mermaid-label-bg-color)}.edgeLabel,.edgeLabel rect{fill:var(--md-mermaid-label-bg-color);color:var(--md-mermaid-edge-color)}.edgePath .path,.flowchart-link{stroke:var(--md-mermaid-edge-color);stroke-width:.05rem}.edgePath .arrowheadPath{fill:var(--md-mermaid-edge-color);stroke:none}.cluster rect{fill:var(--md-default-fg-color--lightest);stroke:var(--md-default-fg-color--lighter)}.cluster span{color:var(--md-mermaid-label-fg-color);font-family:var(--md-mermaid-font-family)}g #flowchart-circleEnd,g #flowchart-circleStart,g #flowchart-crossEnd,g #flowchart-crossStart,g #flowchart-pointEnd,g #flowchart-pointStart{stroke:none}g.classGroup line,g.classGroup rect{fill:var(--md-mermaid-node-bg-color);stroke:var(--md-mermaid-node-fg-color)}g.classGroup text{fill:var(--md-mermaid-label-fg-color);font-family:var(--md-mermaid-font-family)}.classLabel .box{fill:var(--md-mermaid-label-bg-color);background-color:var(--md-mermaid-label-bg-color);opacity:1}.classLabel .label{fill:var(--md-mermaid-label-fg-color);font-family:var(--md-mermaid-font-family)}.node .divider{stroke:var(--md-mermaid-node-fg-color)}.relation{stroke:var(--md-mermaid-edge-color)}.cardinality{fill:var(--md-mermaid-label-fg-color);font-family:var(--md-mermaid-font-family)}.cardinality text{fill:inherit!important}defs #classDiagram-compositionEnd,defs #classDiagram-compositionStart,defs #classDiagram-dependencyEnd,defs #classDiagram-dependencyStart,defs #classDiagram-extensionEnd,defs #classDiagram-extensionStart{fill:var(--md-mermaid-edge-color)!important;stroke:var(--md-mermaid-edge-color)!important}defs #classDiagram-aggregationEnd,defs #classDiagram-aggregationStart{fill:var(--md-mermaid-label-bg-color)!important;stroke:var(--md-mermaid-edge-color)!important}g.stateGroup rect{fill:var(--md-mermaid-node-bg-color);stroke:var(--md-mermaid-node-fg-color)}g.stateGroup .state-title{fill:var(--md-mermaid-label-fg-color)!important;font-family:var(--md-mermaid-font-family)}g.stateGroup .composit{fill:var(--md-mermaid-label-bg-color)}.nodeLabel{color:var(--md-mermaid-label-fg-color);font-family:var(--md-mermaid-font-family)}.node circle.state-end,.node circle.state-start,.start-state{fill:var(--md-mermaid-edge-color);stroke:none}.end-state-inner,.end-state-outer{fill:var(--md-mermaid-edge-color)}.end-state-inner,.node circle.state-end{stroke:var(--md-mermaid-label-bg-color)}.transition{stroke:var(--md-mermaid-edge-color)}[id^=state-fork] rect,[id^=state-join] rect{fill:var(--md-mermaid-edge-color)!important;stroke:none!important}.statediagram-cluster.statediagram-cluster .inner{fill:var(--md-default-bg-color)}.statediagram-cluster rect{fill:var(--md-mermaid-node-bg-color);stroke:var(--md-mermaid-node-fg-color)}.statediagram-state rect.divider{fill:var(--md-default-fg-color--lightest);stroke:var(--md-default-fg-color--lighter)}defs #statediagram-barbEnd{stroke:var(--md-mermaid-edge-color)}.attributeBoxEven,.attributeBoxOdd{fill:var(--md-mermaid-node-bg-color);stroke:var(--md-mermaid-node-fg-color)}.entityBox{fill:var(--md-mermaid-label-bg-color);stroke:var(--md-mermaid-node-fg-color)}.entityLabel{fill:var(--md-mermaid-label-fg-color);font-family:var(--md-mermaid-font-family)}.relationshipLabelBox{fill:var(--md-mermaid-label-bg-color);fill-opacity:1;background-color:var(--md-mermaid-label-bg-color);opacity:1}.relationshipLabel{fill:var(--md-mermaid-label-fg-color)}.relationshipLine{stroke:var(--md-mermaid-edge-color)}defs #ONE_OR_MORE_END *,defs #ONE_OR_MORE_START *,defs #ONLY_ONE_END *,defs #ONLY_ONE_START *,defs #ZERO_OR_MORE_END *,defs #ZERO_OR_MORE_START *,defs #ZERO_OR_ONE_END *,defs #ZERO_OR_ONE_START *{stroke:var(--md-mermaid-edge-color)!important}defs #ZERO_OR_MORE_END circle,defs #ZERO_OR_MORE_START circle{fill:var(--md-mermaid-label-bg-color)}.actor{fill:var(--md-mermaid-sequence-actor-bg-color);stroke:var(--md-mermaid-sequence-actor-border-color)}text.actor>tspan{fill:var(--md-mermaid-sequence-actor-fg-color);font-family:var(--md-mermaid-font-family)}line{stroke:var(--md-mermaid-sequence-actor-line-color)}.actor-man circle,.actor-man line{fill:var(--md-mermaid-sequence-actorman-bg-color);stroke:var(--md-mermaid-sequence-actorman-line-color)}.messageLine0,.messageLine1{stroke:var(--md-mermaid-sequence-message-line-color)}.note{fill:var(--md-mermaid-sequence-note-bg-color);stroke:var(--md-mermaid-sequence-note-border-color)}.loopText,.loopText>tspan,.messageText,.noteText>tspan{stroke:none;font-family:var(--md-mermaid-font-family)!important}.messageText{fill:var(--md-mermaid-sequence-message-fg-color)}.loopText,.loopText>tspan{fill:var(--md-mermaid-sequence-loop-fg-color)}.noteText>tspan{fill:var(--md-mermaid-sequence-note-fg-color)}#arrowhead path{fill:var(--md-mermaid-sequence-message-line-color);stroke:none}.loopLine{fill:var(--md-mermaid-sequence-loop-bg-color);stroke:var(--md-mermaid-sequence-loop-border-color)}.labelBox{fill:var(--md-mermaid-sequence-label-bg-color);stroke:none}.labelText,.labelText>span{fill:var(--md-mermaid-sequence-label-fg-color);font-family:var(--md-mermaid-font-family)}.sequenceNumber{fill:var(--md-mermaid-sequence-number-fg-color)}rect.rect{fill:var(--md-mermaid-sequence-box-bg-color);stroke:none}rect.rect+text.text{fill:var(--md-mermaid-sequence-box-fg-color)}defs #sequencenumber{fill:var(--md-mermaid-sequence-number-bg-color)!important}";var zr,wa=0;function Sa(){return typeof mermaid=="undefined"||mermaid instanceof Element?ht("https://unpkg.com/mermaid@9.4.3/dist/mermaid.min.js"):j(void 0)}function On(e){return e.classList.remove("mermaid"),zr||(zr=Sa().pipe(w(()=>mermaid.initialize({startOnLoad:!1,themeCSS:Tn,sequence:{actorFontSize:"16px",messageFontSize:"16px",noteFontSize:"16px"}})),m(()=>{}),J(1))),zr.subscribe(()=>{e.classList.add("mermaid");let t=`__mermaid_${wa++}`,r=T("div",{class:"mermaid"}),o=e.textContent;mermaid.mermaidAPI.render(t,o,(n,i)=>{let s=r.attachShadow({mode:"closed"});s.innerHTML=n,e.replaceWith(r),i==null||i(s)})}),zr.pipe(m(()=>({ref:e})))}var Mn=T("table");function Ln(e){return e.replaceWith(Mn),Mn.replaceWith(dn(e)),j({ref:e})}function Ta(e){let t=q(":scope > input",e),r=t.find(o=>o.checked)||t[0];return _(...t.map(o=>h(o,"change").pipe(m(()=>U(`label[for="${o.id}"]`))))).pipe(V(U(`label[for="${r.id}"]`)),m(o=>({active:o})))}function _n(e,{viewport$:t}){let r=Ur("prev");e.append(r);let o=Ur("next");e.append(o);let n=U(".tabbed-labels",e);return H(()=>{let i=new x,s=i.pipe(Z(),re(!0));return B([i,ye(e)]).pipe(Ce(1,Oe),Y(s)).subscribe({next([{active:a},c]){let p=Je(a),{width:l}=he(a);e.style.setProperty("--md-indicator-x",`${p.x}px`),e.style.setProperty("--md-indicator-width",`${l}px`);let f=er(n);(p.xf.x+c.width)&&n.scrollTo({left:Math.max(0,p.x-16),behavior:"smooth"})},complete(){e.style.removeProperty("--md-indicator-x"),e.style.removeProperty("--md-indicator-width")}}),B([dt(n),ye(n)]).pipe(Y(s)).subscribe(([a,c])=>{let p=bt(n);r.hidden=a.x<16,o.hidden=a.x>p.width-c.width-16}),_(h(r,"click").pipe(m(()=>-1)),h(o,"click").pipe(m(()=>1))).pipe(Y(s)).subscribe(a=>{let{width:c}=he(n);n.scrollBy({left:c*a,behavior:"smooth"})}),te("content.tabs.link")&&i.pipe(je(1),ne(t)).subscribe(([{active:a},{offset:c}])=>{let p=a.innerText.trim();if(a.hasAttribute("data-md-switching"))a.removeAttribute("data-md-switching");else{let l=e.offsetTop-c.y;for(let u of q("[data-tabs]"))for(let d of q(":scope > input",u)){let v=U(`label[for="${d.id}"]`);if(v!==a&&v.innerText.trim()===p){v.setAttribute("data-md-switching",""),d.click();break}}window.scrollTo({top:e.offsetTop-l});let f=__md_get("__tabs")||[];__md_set("__tabs",[...new Set([p,...f])])}}),i.pipe(Y(s)).subscribe(()=>{for(let a of q("audio, video",e))a.pause()}),Ta(e).pipe(w(a=>i.next(a)),A(()=>i.complete()),m(a=>R({ref:e},a)))}).pipe(rt(ae))}function An(e,{viewport$:t,target$:r,print$:o}){return _(...q(".annotate:not(.highlight)",e).map(n=>gn(n,{target$:r,print$:o})),...q("pre:not(.mermaid) > code",e).map(n=>wn(n,{target$:r,print$:o})),...q("pre.mermaid",e).map(n=>On(n)),...q("table:not([class])",e).map(n=>Ln(n)),...q("details",e).map(n=>Sn(n,{target$:r,print$:o})),...q("[data-tabs]",e).map(n=>_n(n,{viewport$:t})))}function Oa(e,{alert$:t}){return t.pipe(E(r=>_(j(!0),j(!1).pipe(ze(2e3))).pipe(m(o=>({message:r,active:o})))))}function Cn(e,t){let r=U(".md-typeset",e);return H(()=>{let o=new x;return o.subscribe(({message:n,active:i})=>{e.classList.toggle("md-dialog--active",i),r.textContent=n}),Oa(e,t).pipe(w(n=>o.next(n)),A(()=>o.complete()),m(n=>R({ref:e},n)))})}function Ma({viewport$:e}){if(!te("header.autohide"))return j(!1);let t=e.pipe(m(({offset:{y:n}})=>n),Le(2,1),m(([n,i])=>[nMath.abs(i-n.y)>100),m(([,[n]])=>n),X()),o=We("search");return B([e,o]).pipe(m(([{offset:n},i])=>n.y>400&&!i),X(),E(n=>n?r:j(!1)),V(!1))}function kn(e,t){return H(()=>B([ye(e),Ma(t)])).pipe(m(([{height:r},o])=>({height:r,hidden:o})),X((r,o)=>r.height===o.height&&r.hidden===o.hidden),J(1))}function Hn(e,{header$:t,main$:r}){return H(()=>{let o=new x,n=o.pipe(Z(),re(!0));return o.pipe(ee("active"),Ge(t)).subscribe(([{active:i},{hidden:s}])=>{e.classList.toggle("md-header--shadow",i&&!s),e.hidden=s}),r.subscribe(o),t.pipe(Y(n),m(i=>R({ref:e},i)))})}function La(e,{viewport$:t,header$:r}){return ar(e,{viewport$:t,header$:r}).pipe(m(({offset:{y:o}})=>{let{height:n}=he(e);return{active:o>=n}}),ee("active"))}function $n(e,t){return H(()=>{let r=new x;r.subscribe({next({active:n}){e.classList.toggle("md-header__title--active",n)},complete(){e.classList.remove("md-header__title--active")}});let o=se(".md-content h1");return typeof o=="undefined"?L:La(o,t).pipe(w(n=>r.next(n)),A(()=>r.complete()),m(n=>R({ref:e},n)))})}function Rn(e,{viewport$:t,header$:r}){let o=r.pipe(m(({height:i})=>i),X()),n=o.pipe(E(()=>ye(e).pipe(m(({height:i})=>({top:e.offsetTop,bottom:e.offsetTop+i})),ee("bottom"))));return B([o,n,t]).pipe(m(([i,{top:s,bottom:a},{offset:{y:c},size:{height:p}}])=>(p=Math.max(0,p-Math.max(0,s-c,i)-Math.max(0,p+c-a)),{offset:s-i,height:p,active:s-i<=c})),X((i,s)=>i.offset===s.offset&&i.height===s.height&&i.active===s.active))}function _a(e){let t=__md_get("__palette")||{index:e.findIndex(r=>matchMedia(r.getAttribute("data-md-color-media")).matches)};return j(...e).pipe(ce(r=>h(r,"change").pipe(m(()=>r))),V(e[Math.max(0,t.index)]),m(r=>({index:e.indexOf(r),color:{scheme:r.getAttribute("data-md-color-scheme"),primary:r.getAttribute("data-md-color-primary"),accent:r.getAttribute("data-md-color-accent")}})),J(1))}function Pn(e){let t=T("meta",{name:"theme-color"});document.head.appendChild(t);let r=T("meta",{name:"color-scheme"});return document.head.appendChild(r),H(()=>{let o=new x;o.subscribe(i=>{document.body.setAttribute("data-md-color-switching","");for(let[s,a]of Object.entries(i.color))document.body.setAttribute(`data-md-color-${s}`,a);for(let s=0;s{let i=Ee("header"),s=window.getComputedStyle(i);return r.content=s.colorScheme,s.backgroundColor.match(/\d+/g).map(a=>(+a).toString(16).padStart(2,"0")).join("")})).subscribe(i=>t.content=`#${i}`),o.pipe(Se(ae)).subscribe(()=>{document.body.removeAttribute("data-md-color-switching")});let n=q("input",e);return _a(n).pipe(w(i=>o.next(i)),A(()=>o.complete()),m(i=>R({ref:e},i)))})}function In(e,{progress$:t}){return H(()=>{let r=new x;return r.subscribe(({value:o})=>{e.style.setProperty("--md-progress-value",`${o}`)}),t.pipe(w(o=>r.next({value:o})),A(()=>r.complete()),m(o=>({ref:e,value:o})))})}var qr=Ht(Vr());function Aa(e){e.setAttribute("data-md-copying","");let t=e.closest("[data-copy]"),r=t?t.getAttribute("data-copy"):e.innerText;return e.removeAttribute("data-md-copying"),r.trimEnd()}function Fn({alert$:e}){qr.default.isSupported()&&new P(t=>{new qr.default("[data-clipboard-target], [data-clipboard-text]",{text:r=>r.getAttribute("data-clipboard-text")||Aa(U(r.getAttribute("data-clipboard-target")))}).on("success",r=>t.next(r))}).pipe(w(t=>{t.trigger.focus()}),m(()=>be("clipboard.copied"))).subscribe(e)}function Ca(e){if(e.length<2)return[""];let[t,r]=[...e].sort((n,i)=>n.length-i.length).map(n=>n.replace(/[^/]+$/,"")),o=0;if(t===r)o=t.length;else for(;t.charCodeAt(o)===r.charCodeAt(o);)o++;return e.map(n=>n.replace(t.slice(0,o),""))}function cr(e){let t=__md_get("__sitemap",sessionStorage,e);if(t)return j(t);{let r=me();return Zo(new URL("sitemap.xml",e||r.base)).pipe(m(o=>Ca(q("loc",o).map(n=>n.textContent))),de(()=>L),He([]),w(o=>__md_set("__sitemap",o,sessionStorage,e)))}}function jn(e){let t=se("[rel=canonical]",e);typeof t!="undefined"&&(t.href=t.href.replace("//localhost:","//127.0.0.1:"));let r=new Map;for(let o of q(":scope > *",e)){let n=o.outerHTML;for(let i of["href","src"]){let s=o.getAttribute(i);if(s===null)continue;let a=new URL(s,t==null?void 0:t.href),c=o.cloneNode();c.setAttribute(i,`${a}`),n=c.outerHTML;break}r.set(n,o)}return r}function Wn({location$:e,viewport$:t,progress$:r}){let o=me();if(location.protocol==="file:")return L;let n=cr().pipe(m(l=>l.map(f=>`${new URL(f,o.base)}`))),i=h(document.body,"click").pipe(ne(n),E(([l,f])=>{if(!(l.target instanceof Element))return L;let u=l.target.closest("a");if(u===null)return L;if(u.target||l.metaKey||l.ctrlKey)return L;let d=new URL(u.href);return d.search=d.hash="",f.includes(`${d}`)?(l.preventDefault(),j(new URL(u.href))):L}),le());i.pipe(xe(1)).subscribe(()=>{let l=se("link[rel=icon]");typeof l!="undefined"&&(l.href=l.href)}),h(window,"beforeunload").subscribe(()=>{history.scrollRestoration="auto"}),i.pipe(ne(t)).subscribe(([l,{offset:f}])=>{history.scrollRestoration="manual",history.replaceState(f,""),history.pushState(null,"",l)}),i.subscribe(e);let s=e.pipe(V(pe()),ee("pathname"),je(1),E(l=>ir(l,{progress$:r}).pipe(de(()=>(ot(l,!0),L))))),a=new DOMParser,c=s.pipe(E(l=>l.text()),E(l=>{let f=a.parseFromString(l,"text/html");for(let b of["[data-md-component=announce]","[data-md-component=container]","[data-md-component=header-topic]","[data-md-component=outdated]","[data-md-component=logo]","[data-md-component=skip]",...te("navigation.tabs.sticky")?["[data-md-component=tabs]"]:[]]){let z=se(b),K=se(b,f);typeof z!="undefined"&&typeof K!="undefined"&&z.replaceWith(K)}let u=jn(document.head),d=jn(f.head);for(let[b,z]of d)z.getAttribute("rel")==="stylesheet"||z.hasAttribute("src")||(u.has(b)?u.delete(b):document.head.appendChild(z));for(let b of u.values())b.getAttribute("rel")==="stylesheet"||b.hasAttribute("src")||b.remove();let v=Ee("container");return Fe(q("script",v)).pipe(E(b=>{let z=f.createElement("script");if(b.src){for(let K of b.getAttributeNames())z.setAttribute(K,b.getAttribute(K));return b.replaceWith(z),new P(K=>{z.onload=()=>K.complete()})}else return z.textContent=b.textContent,b.replaceWith(z),L}),Z(),re(f))}),le());return h(window,"popstate").pipe(m(pe)).subscribe(e),e.pipe(V(pe()),Le(2,1),M(([l,f])=>l.pathname===f.pathname&&l.hash!==f.hash),m(([,l])=>l)).subscribe(l=>{var f,u;history.state!==null||!l.hash?window.scrollTo(0,(u=(f=history.state)==null?void 0:f.y)!=null?u:0):(history.scrollRestoration="auto",nr(l.hash),history.scrollRestoration="manual")}),e.pipe(Cr(i),V(pe()),Le(2,1),M(([l,f])=>l.pathname===f.pathname&&l.hash===f.hash),m(([,l])=>l)).subscribe(l=>{history.scrollRestoration="auto",nr(l.hash),history.scrollRestoration="manual",history.back()}),c.pipe(ne(e)).subscribe(([,l])=>{var f,u;history.state!==null||!l.hash?window.scrollTo(0,(u=(f=history.state)==null?void 0:f.y)!=null?u:0):nr(l.hash)}),t.pipe(ee("offset"),ke(100)).subscribe(({offset:l})=>{history.replaceState(l,"")}),c}var Dn=Ht(Un());function Vn(e){let t=e.separator.split("|").map(n=>n.replace(/(\(\?[!=<][^)]+\))/g,"").length===0?"\uFFFD":n).join("|"),r=new RegExp(t,"img"),o=(n,i,s)=>`${i}${s}`;return n=>{n=n.replace(/[\s*+\-:~^]+/g," ").trim();let i=new RegExp(`(^|${e.separator}|)(${n.replace(/[|\\{}()[\]^$+*?.-]/g,"\\$&").replace(r,"|")})`,"img");return s=>(0,Dn.default)(s).replace(i,o).replace(/<\/mark>(\s+)]*>/img,"$1")}}function Mt(e){return e.type===1}function pr(e){return e.type===3}function zn(e,t){let r=an(e);return _(j(location.protocol!=="file:"),We("search")).pipe($e(o=>o),E(()=>t)).subscribe(({config:o,docs:n})=>r.next({type:0,data:{config:o,docs:n,options:{suggest:te("search.suggest")}}})),r}function qn({document$:e}){let t=me(),r=Ne(new URL("../versions.json",t.base)).pipe(de(()=>L)),o=r.pipe(m(n=>{let[,i]=t.base.match(/([^/]+)\/?$/);return n.find(({version:s,aliases:a})=>s===i||a.includes(i))||n[0]}));r.pipe(m(n=>new Map(n.map(i=>[`${new URL(`../${i.version}/`,t.base)}`,i]))),E(n=>h(document.body,"click").pipe(M(i=>!i.metaKey&&!i.ctrlKey),ne(o),E(([i,s])=>{if(i.target instanceof Element){let a=i.target.closest("a");if(a&&!a.target&&n.has(a.href)){let c=a.href;return!i.target.closest(".md-version")&&n.get(c)===s?L:(i.preventDefault(),j(c))}}return L}),E(i=>{let{version:s}=n.get(i);return cr(new URL(i)).pipe(m(a=>{let p=pe().href.replace(t.base,"");return a.includes(p.split("#")[0])?new URL(`../${s}/${p}`,t.base):new URL(i)}))})))).subscribe(n=>ot(n,!0)),B([r,o]).subscribe(([n,i])=>{U(".md-header__topic").appendChild(hn(n,i))}),e.pipe(E(()=>o)).subscribe(n=>{var s;let i=__md_get("__outdated",sessionStorage);if(i===null){i=!0;let a=((s=t.version)==null?void 0:s.default)||"latest";Array.isArray(a)||(a=[a]);e:for(let c of a)for(let p of n.aliases.concat(n.version))if(new RegExp(c,"i").test(p)){i=!1;break e}__md_set("__outdated",i,sessionStorage)}if(i)for(let a of oe("outdated"))a.hidden=!1})}function Pa(e,{worker$:t}){let{searchParams:r}=pe();r.has("q")&&(Ke("search",!0),e.value=r.get("q"),e.focus(),We("search").pipe($e(i=>!i)).subscribe(()=>{let i=pe();i.searchParams.delete("q"),history.replaceState({},"",`${i}`)}));let o=Zt(e),n=_(t.pipe($e(Mt)),h(e,"keyup"),o).pipe(m(()=>e.value),X());return B([n,o]).pipe(m(([i,s])=>({value:i,focus:s})),J(1))}function Kn(e,{worker$:t}){let r=new x,o=r.pipe(Z(),re(!0));B([t.pipe($e(Mt)),r],(i,s)=>s).pipe(ee("value")).subscribe(({value:i})=>t.next({type:2,data:i})),r.pipe(ee("focus")).subscribe(({focus:i})=>{i&&Ke("search",i)}),h(e.form,"reset").pipe(Y(o)).subscribe(()=>e.focus());let n=U("header [for=__search]");return h(n,"click").subscribe(()=>e.focus()),Pa(e,{worker$:t}).pipe(w(i=>r.next(i)),A(()=>r.complete()),m(i=>R({ref:e},i)),J(1))}function Qn(e,{worker$:t,query$:r}){let o=new x,n=Ko(e.parentElement).pipe(M(Boolean)),i=e.parentElement,s=U(":scope > :first-child",e),a=U(":scope > :last-child",e);We("search").subscribe(l=>a.setAttribute("role",l?"list":"presentation")),o.pipe(ne(r),$r(t.pipe($e(Mt)))).subscribe(([{items:l},{value:f}])=>{switch(l.length){case 0:s.textContent=f.length?be("search.result.none"):be("search.result.placeholder");break;case 1:s.textContent=be("search.result.one");break;default:let u=tr(l.length);s.textContent=be("search.result.other",u)}});let c=o.pipe(w(()=>a.innerHTML=""),E(({items:l})=>_(j(...l.slice(0,10)),j(...l.slice(10)).pipe(Le(4),Ir(n),E(([f])=>f)))),m(fn),le());return c.subscribe(l=>a.appendChild(l)),c.pipe(ce(l=>{let f=se("details",l);return typeof f=="undefined"?L:h(f,"toggle").pipe(Y(o),m(()=>f))})).subscribe(l=>{l.open===!1&&l.offsetTop<=i.scrollTop&&i.scrollTo({top:l.offsetTop})}),t.pipe(M(pr),m(({data:l})=>l)).pipe(w(l=>o.next(l)),A(()=>o.complete()),m(l=>R({ref:e},l)))}function Ia(e,{query$:t}){return t.pipe(m(({value:r})=>{let o=pe();return o.hash="",r=r.replace(/\s+/g,"+").replace(/&/g,"%26").replace(/=/g,"%3D"),o.search=`q=${r}`,{url:o}}))}function Yn(e,t){let r=new x,o=r.pipe(Z(),re(!0));return r.subscribe(({url:n})=>{e.setAttribute("data-clipboard-text",e.href),e.href=`${n}`}),h(e,"click").pipe(Y(o)).subscribe(n=>n.preventDefault()),Ia(e,t).pipe(w(n=>r.next(n)),A(()=>r.complete()),m(n=>R({ref:e},n)))}function Bn(e,{worker$:t,keyboard$:r}){let o=new x,n=Ee("search-query"),i=_(h(n,"keydown"),h(n,"focus")).pipe(Se(ae),m(()=>n.value),X());return o.pipe(Ge(i),m(([{suggest:a},c])=>{let p=c.split(/([\s-]+)/);if(a!=null&&a.length&&p[p.length-1]){let l=a[a.length-1];l.startsWith(p[p.length-1])&&(p[p.length-1]=l)}else p.length=0;return p})).subscribe(a=>e.innerHTML=a.join("").replace(/\s/g," ")),r.pipe(M(({mode:a})=>a==="search")).subscribe(a=>{switch(a.type){case"ArrowRight":e.innerText.length&&n.selectionStart===n.value.length&&(n.value=e.innerText);break}}),t.pipe(M(pr),m(({data:a})=>a)).pipe(w(a=>o.next(a)),A(()=>o.complete()),m(()=>({ref:e})))}function Gn(e,{index$:t,keyboard$:r}){let o=me();try{let n=zn(o.search,t),i=Ee("search-query",e),s=Ee("search-result",e);h(e,"click").pipe(M(({target:c})=>c instanceof Element&&!!c.closest("a"))).subscribe(()=>Ke("search",!1)),r.pipe(M(({mode:c})=>c==="search")).subscribe(c=>{let p=Re();switch(c.type){case"Enter":if(p===i){let l=new Map;for(let f of q(":first-child [href]",s)){let u=f.firstElementChild;l.set(f,parseFloat(u.getAttribute("data-md-score")))}if(l.size){let[[f]]=[...l].sort(([,u],[,d])=>d-u);f.click()}c.claim()}break;case"Escape":case"Tab":Ke("search",!1),i.blur();break;case"ArrowUp":case"ArrowDown":if(typeof p=="undefined")i.focus();else{let l=[i,...q(":not(details) > [href], summary, details[open] [href]",s)],f=Math.max(0,(Math.max(0,l.indexOf(p))+l.length+(c.type==="ArrowUp"?-1:1))%l.length);l[f].focus()}c.claim();break;default:i!==Re()&&i.focus()}}),r.pipe(M(({mode:c})=>c==="global")).subscribe(c=>{switch(c.type){case"f":case"s":case"/":i.focus(),i.select(),c.claim();break}});let a=Kn(i,{worker$:n});return _(a,Qn(s,{worker$:n,query$:a})).pipe(qe(...oe("search-share",e).map(c=>Yn(c,{query$:a})),...oe("search-suggest",e).map(c=>Bn(c,{worker$:n,keyboard$:r}))))}catch(n){return e.hidden=!0,Ve}}function Jn(e,{index$:t,location$:r}){return B([t,r.pipe(V(pe()),M(o=>!!o.searchParams.get("h")))]).pipe(m(([o,n])=>Vn(o.config)(n.searchParams.get("h"))),m(o=>{var s;let n=new Map,i=document.createNodeIterator(e,NodeFilter.SHOW_TEXT);for(let a=i.nextNode();a;a=i.nextNode())if((s=a.parentElement)!=null&&s.offsetHeight){let c=a.textContent,p=o(c);p.length>c.length&&n.set(a,p)}for(let[a,c]of n){let{childNodes:p}=T("span",null,c);a.replaceWith(...Array.from(p))}return{ref:e,nodes:n}}))}function Fa(e,{viewport$:t,main$:r}){let o=e.closest(".md-grid"),n=o.offsetTop-o.parentElement.offsetTop;return B([r,t]).pipe(m(([{offset:i,height:s},{offset:{y:a}}])=>(s=s+Math.min(n,Math.max(0,a-i))-n,{height:s,locked:a>=i+n})),X((i,s)=>i.height===s.height&&i.locked===s.locked))}function Kr(e,o){var n=o,{header$:t}=n,r=eo(n,["header$"]);let i=U(".md-sidebar__scrollwrap",e),{y:s}=Je(i);return H(()=>{let a=new x,c=a.pipe(Z(),re(!0)),p=a.pipe(Ce(0,Oe));return p.pipe(ne(t)).subscribe({next([{height:l},{height:f}]){i.style.height=`${l-2*s}px`,e.style.top=`${f}px`},complete(){i.style.height="",e.style.top=""}}),p.pipe($e()).subscribe(()=>{for(let l of q(".md-nav__link--active[href]",e)){if(!l.clientHeight)continue;let f=l.closest(".md-sidebar__scrollwrap");if(typeof f!="undefined"){let u=l.offsetTop-f.offsetTop,{height:d}=he(f);f.scrollTo({top:u-d/2})}}}),ge(q("label[tabindex]",e)).pipe(ce(l=>h(l,"click").pipe(Se(ae),m(()=>l),Y(c)))).subscribe(l=>{let f=U(`[id="${l.htmlFor}"]`);U(`[aria-labelledby="${l.id}"]`).setAttribute("aria-expanded",`${f.checked}`)}),Fa(e,r).pipe(w(l=>a.next(l)),A(()=>a.complete()),m(l=>R({ref:e},l)))})}function Xn(e,t){if(typeof t!="undefined"){let r=`https://api.github.com/repos/${e}/${t}`;return St(Ne(`${r}/releases/latest`).pipe(de(()=>L),m(o=>({version:o.tag_name})),He({})),Ne(r).pipe(de(()=>L),m(o=>({stars:o.stargazers_count,forks:o.forks_count})),He({}))).pipe(m(([o,n])=>R(R({},o),n)))}else{let r=`https://api.github.com/users/${e}`;return Ne(r).pipe(m(o=>({repositories:o.public_repos})),He({}))}}function Zn(e,t){let r=`https://${e}/api/v4/projects/${encodeURIComponent(t)}`;return Ne(r).pipe(de(()=>L),m(({star_count:o,forks_count:n})=>({stars:o,forks:n})),He({}))}function ei(e){let t=e.match(/^.+github\.com\/([^/]+)\/?([^/]+)?/i);if(t){let[,r,o]=t;return Xn(r,o)}if(t=e.match(/^.+?([^/]*gitlab[^/]+)\/(.+?)\/?$/i),t){let[,r,o]=t;return Zn(r,o)}return L}var ja;function Wa(e){return ja||(ja=H(()=>{let t=__md_get("__source",sessionStorage);if(t)return j(t);if(oe("consent").length){let o=__md_get("__consent");if(!(o&&o.github))return L}return ei(e.href).pipe(w(o=>__md_set("__source",o,sessionStorage)))}).pipe(de(()=>L),M(t=>Object.keys(t).length>0),m(t=>({facts:t})),J(1)))}function ti(e){let t=U(":scope > :last-child",e);return H(()=>{let r=new x;return r.subscribe(({facts:o})=>{t.appendChild(un(o)),t.classList.add("md-source__repository--active")}),Wa(e).pipe(w(o=>r.next(o)),A(()=>r.complete()),m(o=>R({ref:e},o)))})}function Na(e,{viewport$:t,header$:r}){return ye(document.body).pipe(E(()=>ar(e,{header$:r,viewport$:t})),m(({offset:{y:o}})=>({hidden:o>=10})),ee("hidden"))}function ri(e,t){return H(()=>{let r=new x;return r.subscribe({next({hidden:o}){e.hidden=o},complete(){e.hidden=!1}}),(te("navigation.tabs.sticky")?j({hidden:!1}):Na(e,t)).pipe(w(o=>r.next(o)),A(()=>r.complete()),m(o=>R({ref:e},o)))})}function Ua(e,{viewport$:t,header$:r}){let o=new Map,n=q("[href^=\\#]",e);for(let a of n){let c=decodeURIComponent(a.hash.substring(1)),p=se(`[id="${c}"]`);typeof p!="undefined"&&o.set(a,p)}let i=r.pipe(ee("height"),m(({height:a})=>{let c=Ee("main"),p=U(":scope > :first-child",c);return a+.8*(p.offsetTop-c.offsetTop)}),le());return ye(document.body).pipe(ee("height"),E(a=>H(()=>{let c=[];return j([...o].reduce((p,[l,f])=>{for(;c.length&&o.get(c[c.length-1]).tagName>=f.tagName;)c.pop();let u=f.offsetTop;for(;!u&&f.parentElement;)f=f.parentElement,u=f.offsetTop;let d=f.offsetParent;for(;d;d=d.offsetParent)u+=d.offsetTop;return p.set([...c=[...c,l]].reverse(),u)},new Map))}).pipe(m(c=>new Map([...c].sort(([,p],[,l])=>p-l))),Ge(i),E(([c,p])=>t.pipe(kr(([l,f],{offset:{y:u},size:d})=>{let v=u+d.height>=Math.floor(a.height);for(;f.length;){let[,b]=f[0];if(b-p=u&&!v)f=[l.pop(),...f];else break}return[l,f]},[[],[...c]]),X((l,f)=>l[0]===f[0]&&l[1]===f[1])))))).pipe(m(([a,c])=>({prev:a.map(([p])=>p),next:c.map(([p])=>p)})),V({prev:[],next:[]}),Le(2,1),m(([a,c])=>a.prev.length{let i=new x,s=i.pipe(Z(),re(!0));if(i.subscribe(({prev:a,next:c})=>{for(let[p]of c)p.classList.remove("md-nav__link--passed"),p.classList.remove("md-nav__link--active");for(let[p,[l]]of a.entries())l.classList.add("md-nav__link--passed"),l.classList.toggle("md-nav__link--active",p===a.length-1)}),te("toc.follow")){let a=_(t.pipe(ke(1),m(()=>{})),t.pipe(ke(250),m(()=>"smooth")));i.pipe(M(({prev:c})=>c.length>0),Ge(o.pipe(Se(ae))),ne(a)).subscribe(([[{prev:c}],p])=>{let[l]=c[c.length-1];if(l.offsetHeight){let f=zo(l);if(typeof f!="undefined"){let u=l.offsetTop-f.offsetTop,{height:d}=he(f);f.scrollTo({top:u-d/2,behavior:p})}}})}return te("navigation.tracking")&&t.pipe(Y(s),ee("offset"),ke(250),je(1),Y(n.pipe(je(1))),Tt({delay:250}),ne(i)).subscribe(([,{prev:a}])=>{let c=pe(),p=a[a.length-1];if(p&&p.length){let[l]=p,{hash:f}=new URL(l.href);c.hash!==f&&(c.hash=f,history.replaceState({},"",`${c}`))}else c.hash="",history.replaceState({},"",`${c}`)}),Ua(e,{viewport$:t,header$:r}).pipe(w(a=>i.next(a)),A(()=>i.complete()),m(a=>R({ref:e},a)))})}function Da(e,{viewport$:t,main$:r,target$:o}){let n=t.pipe(m(({offset:{y:s}})=>s),Le(2,1),m(([s,a])=>s>a&&a>0),X()),i=r.pipe(m(({active:s})=>s));return B([i,n]).pipe(m(([s,a])=>!(s&&a)),X(),Y(o.pipe(je(1))),re(!0),Tt({delay:250}),m(s=>({hidden:s})))}function ni(e,{viewport$:t,header$:r,main$:o,target$:n}){let i=new x,s=i.pipe(Z(),re(!0));return i.subscribe({next({hidden:a}){e.hidden=a,a?(e.setAttribute("tabindex","-1"),e.blur()):e.removeAttribute("tabindex")},complete(){e.style.top="",e.hidden=!0,e.removeAttribute("tabindex")}}),r.pipe(Y(s),ee("height")).subscribe(({height:a})=>{e.style.top=`${a+16}px`}),h(e,"click").subscribe(a=>{a.preventDefault(),window.scrollTo({top:0})}),Da(e,{viewport$:t,main$:o,target$:n}).pipe(w(a=>i.next(a)),A(()=>i.complete()),m(a=>R({ref:e},a)))}function ii({document$:e,tablet$:t}){e.pipe(E(()=>q(".md-toggle--indeterminate")),w(r=>{r.indeterminate=!0,r.checked=!1}),ce(r=>h(r,"change").pipe(Rr(()=>r.classList.contains("md-toggle--indeterminate")),m(()=>r))),ne(t)).subscribe(([r,o])=>{r.classList.remove("md-toggle--indeterminate"),o&&(r.checked=!1)})}function Va(){return/(iPad|iPhone|iPod)/.test(navigator.userAgent)}function ai({document$:e}){e.pipe(E(()=>q("[data-md-scrollfix]")),w(t=>t.removeAttribute("data-md-scrollfix")),M(Va),ce(t=>h(t,"touchstart").pipe(m(()=>t)))).subscribe(t=>{let r=t.scrollTop;r===0?t.scrollTop=1:r+t.offsetHeight===t.scrollHeight&&(t.scrollTop=r-1)})}function si({viewport$:e,tablet$:t}){B([We("search"),t]).pipe(m(([r,o])=>r&&!o),E(r=>j(r).pipe(ze(r?400:100))),ne(e)).subscribe(([r,{offset:{y:o}}])=>{if(r)document.body.setAttribute("data-md-scrolllock",""),document.body.style.top=`-${o}px`;else{let n=-1*parseInt(document.body.style.top,10);document.body.removeAttribute("data-md-scrolllock"),document.body.style.top="",n&&window.scrollTo(0,n)}})}Object.entries||(Object.entries=function(e){let t=[];for(let r of Object.keys(e))t.push([r,e[r]]);return t});Object.values||(Object.values=function(e){let t=[];for(let r of Object.keys(e))t.push(e[r]);return t});typeof Element!="undefined"&&(Element.prototype.scrollTo||(Element.prototype.scrollTo=function(e,t){typeof e=="object"?(this.scrollLeft=e.left,this.scrollTop=e.top):(this.scrollLeft=e,this.scrollTop=t)}),Element.prototype.replaceWith||(Element.prototype.replaceWith=function(...e){let t=this.parentNode;if(t){e.length===0&&t.removeChild(this);for(let r=e.length-1;r>=0;r--){let o=e[r];typeof o=="string"?o=document.createTextNode(o):o.parentNode&&o.parentNode.removeChild(o),r?t.insertBefore(this.previousSibling,o):t.replaceChild(o,this)}}}));function za(){return location.protocol==="file:"?ht(`${new URL("search/search_index.js",Qr.base)}`).pipe(m(()=>__index),J(1)):Ne(new URL("search/search_index.json",Qr.base))}document.documentElement.classList.remove("no-js");document.documentElement.classList.add("js");var nt=No(),_t=Bo(),gt=Jo(_t),Yr=Yo(),Te=nn(),lr=Fr("(min-width: 960px)"),pi=Fr("(min-width: 1220px)"),li=Xo(),Qr=me(),mi=document.forms.namedItem("search")?za():Ve,Br=new x;Fn({alert$:Br});var Gr=new x;te("navigation.instant")&&Wn({location$:_t,viewport$:Te,progress$:Gr}).subscribe(nt);var ci;((ci=Qr.version)==null?void 0:ci.provider)==="mike"&&qn({document$:nt});_(_t,gt).pipe(ze(125)).subscribe(()=>{Ke("drawer",!1),Ke("search",!1)});Yr.pipe(M(({mode:e})=>e==="global")).subscribe(e=>{switch(e.type){case"p":case",":let t=se("link[rel=prev]");typeof t!="undefined"&&ot(t);break;case"n":case".":let r=se("link[rel=next]");typeof r!="undefined"&&ot(r);break;case"Enter":let o=Re();o instanceof HTMLLabelElement&&o.click()}});ii({document$:nt,tablet$:lr});ai({document$:nt});si({viewport$:Te,tablet$:lr});var Xe=kn(Ee("header"),{viewport$:Te}),Lt=nt.pipe(m(()=>Ee("main")),E(e=>Rn(e,{viewport$:Te,header$:Xe})),J(1)),qa=_(...oe("consent").map(e=>cn(e,{target$:gt})),...oe("dialog").map(e=>Cn(e,{alert$:Br})),...oe("header").map(e=>Hn(e,{viewport$:Te,header$:Xe,main$:Lt})),...oe("palette").map(e=>Pn(e)),...oe("progress").map(e=>In(e,{progress$:Gr})),...oe("search").map(e=>Gn(e,{index$:mi,keyboard$:Yr})),...oe("source").map(e=>ti(e))),Ka=H(()=>_(...oe("announce").map(e=>sn(e)),...oe("content").map(e=>An(e,{viewport$:Te,target$:gt,print$:li})),...oe("content").map(e=>te("search.highlight")?Jn(e,{index$:mi,location$:_t}):L),...oe("header-title").map(e=>$n(e,{viewport$:Te,header$:Xe})),...oe("sidebar").map(e=>e.getAttribute("data-md-type")==="navigation"?jr(pi,()=>Kr(e,{viewport$:Te,header$:Xe,main$:Lt})):jr(lr,()=>Kr(e,{viewport$:Te,header$:Xe,main$:Lt}))),...oe("tabs").map(e=>ri(e,{viewport$:Te,header$:Xe})),...oe("toc").map(e=>oi(e,{viewport$:Te,header$:Xe,main$:Lt,target$:gt})),...oe("top").map(e=>ni(e,{viewport$:Te,header$:Xe,main$:Lt,target$:gt})))),fi=nt.pipe(E(()=>Ka),qe(qa),J(1));fi.subscribe();window.document$=nt;window.location$=_t;window.target$=gt;window.keyboard$=Yr;window.viewport$=Te;window.tablet$=lr;window.screen$=pi;window.print$=li;window.alert$=Br;window.progress$=Gr;window.component$=fi;})(); +//# sourceMappingURL=bundle.6c14ae12.min.js.map + diff --git a/assets/javascripts/bundle.6c14ae12.min.js.map b/assets/javascripts/bundle.6c14ae12.min.js.map new file mode 100644 index 0000000..49396ad --- /dev/null +++ b/assets/javascripts/bundle.6c14ae12.min.js.map @@ -0,0 +1,7 @@ +{ + "version": 3, + "sources": ["node_modules/focus-visible/dist/focus-visible.js", "node_modules/clipboard/dist/clipboard.js", "node_modules/escape-html/index.js", "src/templates/assets/javascripts/bundle.ts", "node_modules/rxjs/node_modules/tslib/tslib.es6.js", "node_modules/rxjs/src/internal/util/isFunction.ts", "node_modules/rxjs/src/internal/util/createErrorClass.ts", "node_modules/rxjs/src/internal/util/UnsubscriptionError.ts", "node_modules/rxjs/src/internal/util/arrRemove.ts", "node_modules/rxjs/src/internal/Subscription.ts", "node_modules/rxjs/src/internal/config.ts", "node_modules/rxjs/src/internal/scheduler/timeoutProvider.ts", "node_modules/rxjs/src/internal/util/reportUnhandledError.ts", "node_modules/rxjs/src/internal/util/noop.ts", "node_modules/rxjs/src/internal/NotificationFactories.ts", "node_modules/rxjs/src/internal/util/errorContext.ts", "node_modules/rxjs/src/internal/Subscriber.ts", "node_modules/rxjs/src/internal/symbol/observable.ts", "node_modules/rxjs/src/internal/util/identity.ts", "node_modules/rxjs/src/internal/util/pipe.ts", "node_modules/rxjs/src/internal/Observable.ts", "node_modules/rxjs/src/internal/util/lift.ts", "node_modules/rxjs/src/internal/operators/OperatorSubscriber.ts", "node_modules/rxjs/src/internal/scheduler/animationFrameProvider.ts", "node_modules/rxjs/src/internal/util/ObjectUnsubscribedError.ts", "node_modules/rxjs/src/internal/Subject.ts", "node_modules/rxjs/src/internal/scheduler/dateTimestampProvider.ts", "node_modules/rxjs/src/internal/ReplaySubject.ts", "node_modules/rxjs/src/internal/scheduler/Action.ts", "node_modules/rxjs/src/internal/scheduler/intervalProvider.ts", "node_modules/rxjs/src/internal/scheduler/AsyncAction.ts", "node_modules/rxjs/src/internal/Scheduler.ts", "node_modules/rxjs/src/internal/scheduler/AsyncScheduler.ts", "node_modules/rxjs/src/internal/scheduler/async.ts", "node_modules/rxjs/src/internal/scheduler/AnimationFrameAction.ts", "node_modules/rxjs/src/internal/scheduler/AnimationFrameScheduler.ts", "node_modules/rxjs/src/internal/scheduler/animationFrame.ts", "node_modules/rxjs/src/internal/observable/empty.ts", "node_modules/rxjs/src/internal/util/isScheduler.ts", "node_modules/rxjs/src/internal/util/args.ts", "node_modules/rxjs/src/internal/util/isArrayLike.ts", "node_modules/rxjs/src/internal/util/isPromise.ts", "node_modules/rxjs/src/internal/util/isInteropObservable.ts", "node_modules/rxjs/src/internal/util/isAsyncIterable.ts", "node_modules/rxjs/src/internal/util/throwUnobservableError.ts", "node_modules/rxjs/src/internal/symbol/iterator.ts", "node_modules/rxjs/src/internal/util/isIterable.ts", "node_modules/rxjs/src/internal/util/isReadableStreamLike.ts", "node_modules/rxjs/src/internal/observable/innerFrom.ts", "node_modules/rxjs/src/internal/util/executeSchedule.ts", "node_modules/rxjs/src/internal/operators/observeOn.ts", "node_modules/rxjs/src/internal/operators/subscribeOn.ts", "node_modules/rxjs/src/internal/scheduled/scheduleObservable.ts", "node_modules/rxjs/src/internal/scheduled/schedulePromise.ts", "node_modules/rxjs/src/internal/scheduled/scheduleArray.ts", "node_modules/rxjs/src/internal/scheduled/scheduleIterable.ts", "node_modules/rxjs/src/internal/scheduled/scheduleAsyncIterable.ts", "node_modules/rxjs/src/internal/scheduled/scheduleReadableStreamLike.ts", "node_modules/rxjs/src/internal/scheduled/scheduled.ts", "node_modules/rxjs/src/internal/observable/from.ts", "node_modules/rxjs/src/internal/observable/of.ts", "node_modules/rxjs/src/internal/observable/throwError.ts", "node_modules/rxjs/src/internal/util/EmptyError.ts", "node_modules/rxjs/src/internal/util/isDate.ts", "node_modules/rxjs/src/internal/operators/map.ts", "node_modules/rxjs/src/internal/util/mapOneOrManyArgs.ts", "node_modules/rxjs/src/internal/util/argsArgArrayOrObject.ts", "node_modules/rxjs/src/internal/util/createObject.ts", "node_modules/rxjs/src/internal/observable/combineLatest.ts", "node_modules/rxjs/src/internal/operators/mergeInternals.ts", "node_modules/rxjs/src/internal/operators/mergeMap.ts", "node_modules/rxjs/src/internal/operators/mergeAll.ts", "node_modules/rxjs/src/internal/operators/concatAll.ts", "node_modules/rxjs/src/internal/observable/concat.ts", "node_modules/rxjs/src/internal/observable/defer.ts", "node_modules/rxjs/src/internal/observable/fromEvent.ts", "node_modules/rxjs/src/internal/observable/fromEventPattern.ts", "node_modules/rxjs/src/internal/observable/timer.ts", "node_modules/rxjs/src/internal/observable/merge.ts", "node_modules/rxjs/src/internal/observable/never.ts", "node_modules/rxjs/src/internal/util/argsOrArgArray.ts", "node_modules/rxjs/src/internal/operators/filter.ts", "node_modules/rxjs/src/internal/observable/zip.ts", "node_modules/rxjs/src/internal/operators/audit.ts", "node_modules/rxjs/src/internal/operators/auditTime.ts", "node_modules/rxjs/src/internal/operators/bufferCount.ts", "node_modules/rxjs/src/internal/operators/catchError.ts", "node_modules/rxjs/src/internal/operators/scanInternals.ts", "node_modules/rxjs/src/internal/operators/combineLatest.ts", "node_modules/rxjs/src/internal/operators/combineLatestWith.ts", "node_modules/rxjs/src/internal/operators/debounceTime.ts", "node_modules/rxjs/src/internal/operators/defaultIfEmpty.ts", "node_modules/rxjs/src/internal/operators/take.ts", "node_modules/rxjs/src/internal/operators/ignoreElements.ts", "node_modules/rxjs/src/internal/operators/mapTo.ts", "node_modules/rxjs/src/internal/operators/delayWhen.ts", "node_modules/rxjs/src/internal/operators/delay.ts", "node_modules/rxjs/src/internal/operators/distinctUntilChanged.ts", "node_modules/rxjs/src/internal/operators/distinctUntilKeyChanged.ts", "node_modules/rxjs/src/internal/operators/throwIfEmpty.ts", "node_modules/rxjs/src/internal/operators/endWith.ts", "node_modules/rxjs/src/internal/operators/finalize.ts", "node_modules/rxjs/src/internal/operators/first.ts", "node_modules/rxjs/src/internal/operators/merge.ts", "node_modules/rxjs/src/internal/operators/mergeWith.ts", "node_modules/rxjs/src/internal/operators/repeat.ts", "node_modules/rxjs/src/internal/operators/sample.ts", "node_modules/rxjs/src/internal/operators/scan.ts", "node_modules/rxjs/src/internal/operators/share.ts", "node_modules/rxjs/src/internal/operators/shareReplay.ts", "node_modules/rxjs/src/internal/operators/skip.ts", "node_modules/rxjs/src/internal/operators/skipUntil.ts", "node_modules/rxjs/src/internal/operators/startWith.ts", "node_modules/rxjs/src/internal/operators/switchMap.ts", "node_modules/rxjs/src/internal/operators/takeUntil.ts", "node_modules/rxjs/src/internal/operators/takeWhile.ts", "node_modules/rxjs/src/internal/operators/tap.ts", "node_modules/rxjs/src/internal/operators/throttle.ts", "node_modules/rxjs/src/internal/operators/throttleTime.ts", "node_modules/rxjs/src/internal/operators/withLatestFrom.ts", "node_modules/rxjs/src/internal/operators/zip.ts", "node_modules/rxjs/src/internal/operators/zipWith.ts", "src/templates/assets/javascripts/browser/document/index.ts", "src/templates/assets/javascripts/browser/element/_/index.ts", "src/templates/assets/javascripts/browser/element/focus/index.ts", "src/templates/assets/javascripts/browser/element/offset/_/index.ts", "src/templates/assets/javascripts/browser/element/offset/content/index.ts", "src/templates/assets/javascripts/utilities/h/index.ts", "src/templates/assets/javascripts/utilities/round/index.ts", "src/templates/assets/javascripts/browser/script/index.ts", "src/templates/assets/javascripts/browser/element/size/_/index.ts", "src/templates/assets/javascripts/browser/element/size/content/index.ts", "src/templates/assets/javascripts/browser/element/visibility/index.ts", "src/templates/assets/javascripts/browser/toggle/index.ts", "src/templates/assets/javascripts/browser/keyboard/index.ts", "src/templates/assets/javascripts/browser/location/_/index.ts", "src/templates/assets/javascripts/browser/location/hash/index.ts", "src/templates/assets/javascripts/browser/media/index.ts", "src/templates/assets/javascripts/browser/request/index.ts", "src/templates/assets/javascripts/browser/viewport/offset/index.ts", "src/templates/assets/javascripts/browser/viewport/size/index.ts", "src/templates/assets/javascripts/browser/viewport/_/index.ts", "src/templates/assets/javascripts/browser/viewport/at/index.ts", "src/templates/assets/javascripts/browser/worker/index.ts", "src/templates/assets/javascripts/_/index.ts", "src/templates/assets/javascripts/components/_/index.ts", "src/templates/assets/javascripts/components/announce/index.ts", "src/templates/assets/javascripts/components/consent/index.ts", "src/templates/assets/javascripts/components/content/annotation/_/index.ts", "src/templates/assets/javascripts/templates/tooltip/index.tsx", "src/templates/assets/javascripts/templates/annotation/index.tsx", "src/templates/assets/javascripts/templates/clipboard/index.tsx", "src/templates/assets/javascripts/templates/search/index.tsx", "src/templates/assets/javascripts/templates/source/index.tsx", "src/templates/assets/javascripts/templates/tabbed/index.tsx", "src/templates/assets/javascripts/templates/table/index.tsx", "src/templates/assets/javascripts/templates/version/index.tsx", "src/templates/assets/javascripts/components/content/annotation/list/index.ts", "src/templates/assets/javascripts/components/content/annotation/block/index.ts", "src/templates/assets/javascripts/components/content/code/_/index.ts", "src/templates/assets/javascripts/components/content/details/index.ts", "src/templates/assets/javascripts/components/content/mermaid/index.css", "src/templates/assets/javascripts/components/content/mermaid/index.ts", "src/templates/assets/javascripts/components/content/table/index.ts", "src/templates/assets/javascripts/components/content/tabs/index.ts", "src/templates/assets/javascripts/components/content/_/index.ts", "src/templates/assets/javascripts/components/dialog/index.ts", "src/templates/assets/javascripts/components/header/_/index.ts", "src/templates/assets/javascripts/components/header/title/index.ts", "src/templates/assets/javascripts/components/main/index.ts", "src/templates/assets/javascripts/components/palette/index.ts", "src/templates/assets/javascripts/components/progress/index.ts", "src/templates/assets/javascripts/integrations/clipboard/index.ts", "src/templates/assets/javascripts/integrations/sitemap/index.ts", "src/templates/assets/javascripts/integrations/instant/index.ts", "src/templates/assets/javascripts/integrations/search/highlighter/index.ts", "src/templates/assets/javascripts/integrations/search/worker/message/index.ts", "src/templates/assets/javascripts/integrations/search/worker/_/index.ts", "src/templates/assets/javascripts/integrations/version/index.ts", "src/templates/assets/javascripts/components/search/query/index.ts", "src/templates/assets/javascripts/components/search/result/index.ts", "src/templates/assets/javascripts/components/search/share/index.ts", "src/templates/assets/javascripts/components/search/suggest/index.ts", "src/templates/assets/javascripts/components/search/_/index.ts", "src/templates/assets/javascripts/components/search/highlight/index.ts", "src/templates/assets/javascripts/components/sidebar/index.ts", "src/templates/assets/javascripts/components/source/facts/github/index.ts", "src/templates/assets/javascripts/components/source/facts/gitlab/index.ts", "src/templates/assets/javascripts/components/source/facts/_/index.ts", "src/templates/assets/javascripts/components/source/_/index.ts", "src/templates/assets/javascripts/components/tabs/index.ts", "src/templates/assets/javascripts/components/toc/index.ts", "src/templates/assets/javascripts/components/top/index.ts", "src/templates/assets/javascripts/patches/indeterminate/index.ts", "src/templates/assets/javascripts/patches/scrollfix/index.ts", "src/templates/assets/javascripts/patches/scrolllock/index.ts", "src/templates/assets/javascripts/polyfills/index.ts"], + "sourcesContent": ["(function (global, factory) {\n typeof exports === 'object' && typeof module !== 'undefined' ? factory() :\n typeof define === 'function' && define.amd ? define(factory) :\n (factory());\n}(this, (function () { 'use strict';\n\n /**\n * Applies the :focus-visible polyfill at the given scope.\n * A scope in this case is either the top-level Document or a Shadow Root.\n *\n * @param {(Document|ShadowRoot)} scope\n * @see https://github.com/WICG/focus-visible\n */\n function applyFocusVisiblePolyfill(scope) {\n var hadKeyboardEvent = true;\n var hadFocusVisibleRecently = false;\n var hadFocusVisibleRecentlyTimeout = null;\n\n var inputTypesAllowlist = {\n text: true,\n search: true,\n url: true,\n tel: true,\n email: true,\n password: true,\n number: true,\n date: true,\n month: true,\n week: true,\n time: true,\n datetime: true,\n 'datetime-local': true\n };\n\n /**\n * Helper function for legacy browsers and iframes which sometimes focus\n * elements like document, body, and non-interactive SVG.\n * @param {Element} el\n */\n function isValidFocusTarget(el) {\n if (\n el &&\n el !== document &&\n el.nodeName !== 'HTML' &&\n el.nodeName !== 'BODY' &&\n 'classList' in el &&\n 'contains' in el.classList\n ) {\n return true;\n }\n return false;\n }\n\n /**\n * Computes whether the given element should automatically trigger the\n * `focus-visible` class being added, i.e. whether it should always match\n * `:focus-visible` when focused.\n * @param {Element} el\n * @return {boolean}\n */\n function focusTriggersKeyboardModality(el) {\n var type = el.type;\n var tagName = el.tagName;\n\n if (tagName === 'INPUT' && inputTypesAllowlist[type] && !el.readOnly) {\n return true;\n }\n\n if (tagName === 'TEXTAREA' && !el.readOnly) {\n return true;\n }\n\n if (el.isContentEditable) {\n return true;\n }\n\n return false;\n }\n\n /**\n * Add the `focus-visible` class to the given element if it was not added by\n * the author.\n * @param {Element} el\n */\n function addFocusVisibleClass(el) {\n if (el.classList.contains('focus-visible')) {\n return;\n }\n el.classList.add('focus-visible');\n el.setAttribute('data-focus-visible-added', '');\n }\n\n /**\n * Remove the `focus-visible` class from the given element if it was not\n * originally added by the author.\n * @param {Element} el\n */\n function removeFocusVisibleClass(el) {\n if (!el.hasAttribute('data-focus-visible-added')) {\n return;\n }\n el.classList.remove('focus-visible');\n el.removeAttribute('data-focus-visible-added');\n }\n\n /**\n * If the most recent user interaction was via the keyboard;\n * and the key press did not include a meta, alt/option, or control key;\n * then the modality is keyboard. Otherwise, the modality is not keyboard.\n * Apply `focus-visible` to any current active element and keep track\n * of our keyboard modality state with `hadKeyboardEvent`.\n * @param {KeyboardEvent} e\n */\n function onKeyDown(e) {\n if (e.metaKey || e.altKey || e.ctrlKey) {\n return;\n }\n\n if (isValidFocusTarget(scope.activeElement)) {\n addFocusVisibleClass(scope.activeElement);\n }\n\n hadKeyboardEvent = true;\n }\n\n /**\n * If at any point a user clicks with a pointing device, ensure that we change\n * the modality away from keyboard.\n * This avoids the situation where a user presses a key on an already focused\n * element, and then clicks on a different element, focusing it with a\n * pointing device, while we still think we're in keyboard modality.\n * @param {Event} e\n */\n function onPointerDown(e) {\n hadKeyboardEvent = false;\n }\n\n /**\n * On `focus`, add the `focus-visible` class to the target if:\n * - the target received focus as a result of keyboard navigation, or\n * - the event target is an element that will likely require interaction\n * via the keyboard (e.g. a text box)\n * @param {Event} e\n */\n function onFocus(e) {\n // Prevent IE from focusing the document or HTML element.\n if (!isValidFocusTarget(e.target)) {\n return;\n }\n\n if (hadKeyboardEvent || focusTriggersKeyboardModality(e.target)) {\n addFocusVisibleClass(e.target);\n }\n }\n\n /**\n * On `blur`, remove the `focus-visible` class from the target.\n * @param {Event} e\n */\n function onBlur(e) {\n if (!isValidFocusTarget(e.target)) {\n return;\n }\n\n if (\n e.target.classList.contains('focus-visible') ||\n e.target.hasAttribute('data-focus-visible-added')\n ) {\n // To detect a tab/window switch, we look for a blur event followed\n // rapidly by a visibility change.\n // If we don't see a visibility change within 100ms, it's probably a\n // regular focus change.\n hadFocusVisibleRecently = true;\n window.clearTimeout(hadFocusVisibleRecentlyTimeout);\n hadFocusVisibleRecentlyTimeout = window.setTimeout(function() {\n hadFocusVisibleRecently = false;\n }, 100);\n removeFocusVisibleClass(e.target);\n }\n }\n\n /**\n * If the user changes tabs, keep track of whether or not the previously\n * focused element had .focus-visible.\n * @param {Event} e\n */\n function onVisibilityChange(e) {\n if (document.visibilityState === 'hidden') {\n // If the tab becomes active again, the browser will handle calling focus\n // on the element (Safari actually calls it twice).\n // If this tab change caused a blur on an element with focus-visible,\n // re-apply the class when the user switches back to the tab.\n if (hadFocusVisibleRecently) {\n hadKeyboardEvent = true;\n }\n addInitialPointerMoveListeners();\n }\n }\n\n /**\n * Add a group of listeners to detect usage of any pointing devices.\n * These listeners will be added when the polyfill first loads, and anytime\n * the window is blurred, so that they are active when the window regains\n * focus.\n */\n function addInitialPointerMoveListeners() {\n document.addEventListener('mousemove', onInitialPointerMove);\n document.addEventListener('mousedown', onInitialPointerMove);\n document.addEventListener('mouseup', onInitialPointerMove);\n document.addEventListener('pointermove', onInitialPointerMove);\n document.addEventListener('pointerdown', onInitialPointerMove);\n document.addEventListener('pointerup', onInitialPointerMove);\n document.addEventListener('touchmove', onInitialPointerMove);\n document.addEventListener('touchstart', onInitialPointerMove);\n document.addEventListener('touchend', onInitialPointerMove);\n }\n\n function removeInitialPointerMoveListeners() {\n document.removeEventListener('mousemove', onInitialPointerMove);\n document.removeEventListener('mousedown', onInitialPointerMove);\n document.removeEventListener('mouseup', onInitialPointerMove);\n document.removeEventListener('pointermove', onInitialPointerMove);\n document.removeEventListener('pointerdown', onInitialPointerMove);\n document.removeEventListener('pointerup', onInitialPointerMove);\n document.removeEventListener('touchmove', onInitialPointerMove);\n document.removeEventListener('touchstart', onInitialPointerMove);\n document.removeEventListener('touchend', onInitialPointerMove);\n }\n\n /**\n * When the polfyill first loads, assume the user is in keyboard modality.\n * If any event is received from a pointing device (e.g. mouse, pointer,\n * touch), turn off keyboard modality.\n * This accounts for situations where focus enters the page from the URL bar.\n * @param {Event} e\n */\n function onInitialPointerMove(e) {\n // Work around a Safari quirk that fires a mousemove on whenever the\n // window blurs, even if you're tabbing out of the page. \u00AF\\_(\u30C4)_/\u00AF\n if (e.target.nodeName && e.target.nodeName.toLowerCase() === 'html') {\n return;\n }\n\n hadKeyboardEvent = false;\n removeInitialPointerMoveListeners();\n }\n\n // For some kinds of state, we are interested in changes at the global scope\n // only. For example, global pointer input, global key presses and global\n // visibility change should affect the state at every scope:\n document.addEventListener('keydown', onKeyDown, true);\n document.addEventListener('mousedown', onPointerDown, true);\n document.addEventListener('pointerdown', onPointerDown, true);\n document.addEventListener('touchstart', onPointerDown, true);\n document.addEventListener('visibilitychange', onVisibilityChange, true);\n\n addInitialPointerMoveListeners();\n\n // For focus and blur, we specifically care about state changes in the local\n // scope. This is because focus / blur events that originate from within a\n // shadow root are not re-dispatched from the host element if it was already\n // the active element in its own scope:\n scope.addEventListener('focus', onFocus, true);\n scope.addEventListener('blur', onBlur, true);\n\n // We detect that a node is a ShadowRoot by ensuring that it is a\n // DocumentFragment and also has a host property. This check covers native\n // implementation and polyfill implementation transparently. If we only cared\n // about the native implementation, we could just check if the scope was\n // an instance of a ShadowRoot.\n if (scope.nodeType === Node.DOCUMENT_FRAGMENT_NODE && scope.host) {\n // Since a ShadowRoot is a special kind of DocumentFragment, it does not\n // have a root element to add a class to. So, we add this attribute to the\n // host element instead:\n scope.host.setAttribute('data-js-focus-visible', '');\n } else if (scope.nodeType === Node.DOCUMENT_NODE) {\n document.documentElement.classList.add('js-focus-visible');\n document.documentElement.setAttribute('data-js-focus-visible', '');\n }\n }\n\n // It is important to wrap all references to global window and document in\n // these checks to support server-side rendering use cases\n // @see https://github.com/WICG/focus-visible/issues/199\n if (typeof window !== 'undefined' && typeof document !== 'undefined') {\n // Make the polyfill helper globally available. This can be used as a signal\n // to interested libraries that wish to coordinate with the polyfill for e.g.,\n // applying the polyfill to a shadow root:\n window.applyFocusVisiblePolyfill = applyFocusVisiblePolyfill;\n\n // Notify interested libraries of the polyfill's presence, in case the\n // polyfill was loaded lazily:\n var event;\n\n try {\n event = new CustomEvent('focus-visible-polyfill-ready');\n } catch (error) {\n // IE11 does not support using CustomEvent as a constructor directly:\n event = document.createEvent('CustomEvent');\n event.initCustomEvent('focus-visible-polyfill-ready', false, false, {});\n }\n\n window.dispatchEvent(event);\n }\n\n if (typeof document !== 'undefined') {\n // Apply the polyfill to the global document, so that no JavaScript\n // coordination is required to use the polyfill in the top-level document:\n applyFocusVisiblePolyfill(document);\n }\n\n})));\n", "/*!\n * clipboard.js v2.0.11\n * https://clipboardjs.com/\n *\n * Licensed MIT \u00A9 Zeno Rocha\n */\n(function webpackUniversalModuleDefinition(root, factory) {\n\tif(typeof exports === 'object' && typeof module === 'object')\n\t\tmodule.exports = factory();\n\telse if(typeof define === 'function' && define.amd)\n\t\tdefine([], factory);\n\telse if(typeof exports === 'object')\n\t\texports[\"ClipboardJS\"] = factory();\n\telse\n\t\troot[\"ClipboardJS\"] = factory();\n})(this, function() {\nreturn /******/ (function() { // webpackBootstrap\n/******/ \tvar __webpack_modules__ = ({\n\n/***/ 686:\n/***/ (function(__unused_webpack_module, __webpack_exports__, __webpack_require__) {\n\n\"use strict\";\n\n// EXPORTS\n__webpack_require__.d(__webpack_exports__, {\n \"default\": function() { return /* binding */ clipboard; }\n});\n\n// EXTERNAL MODULE: ./node_modules/tiny-emitter/index.js\nvar tiny_emitter = __webpack_require__(279);\nvar tiny_emitter_default = /*#__PURE__*/__webpack_require__.n(tiny_emitter);\n// EXTERNAL MODULE: ./node_modules/good-listener/src/listen.js\nvar listen = __webpack_require__(370);\nvar listen_default = /*#__PURE__*/__webpack_require__.n(listen);\n// EXTERNAL MODULE: ./node_modules/select/src/select.js\nvar src_select = __webpack_require__(817);\nvar select_default = /*#__PURE__*/__webpack_require__.n(src_select);\n;// CONCATENATED MODULE: ./src/common/command.js\n/**\n * Executes a given operation type.\n * @param {String} type\n * @return {Boolean}\n */\nfunction command(type) {\n try {\n return document.execCommand(type);\n } catch (err) {\n return false;\n }\n}\n;// CONCATENATED MODULE: ./src/actions/cut.js\n\n\n/**\n * Cut action wrapper.\n * @param {String|HTMLElement} target\n * @return {String}\n */\n\nvar ClipboardActionCut = function ClipboardActionCut(target) {\n var selectedText = select_default()(target);\n command('cut');\n return selectedText;\n};\n\n/* harmony default export */ var actions_cut = (ClipboardActionCut);\n;// CONCATENATED MODULE: ./src/common/create-fake-element.js\n/**\n * Creates a fake textarea element with a value.\n * @param {String} value\n * @return {HTMLElement}\n */\nfunction createFakeElement(value) {\n var isRTL = document.documentElement.getAttribute('dir') === 'rtl';\n var fakeElement = document.createElement('textarea'); // Prevent zooming on iOS\n\n fakeElement.style.fontSize = '12pt'; // Reset box model\n\n fakeElement.style.border = '0';\n fakeElement.style.padding = '0';\n fakeElement.style.margin = '0'; // Move element out of screen horizontally\n\n fakeElement.style.position = 'absolute';\n fakeElement.style[isRTL ? 'right' : 'left'] = '-9999px'; // Move element to the same position vertically\n\n var yPosition = window.pageYOffset || document.documentElement.scrollTop;\n fakeElement.style.top = \"\".concat(yPosition, \"px\");\n fakeElement.setAttribute('readonly', '');\n fakeElement.value = value;\n return fakeElement;\n}\n;// CONCATENATED MODULE: ./src/actions/copy.js\n\n\n\n/**\n * Create fake copy action wrapper using a fake element.\n * @param {String} target\n * @param {Object} options\n * @return {String}\n */\n\nvar fakeCopyAction = function fakeCopyAction(value, options) {\n var fakeElement = createFakeElement(value);\n options.container.appendChild(fakeElement);\n var selectedText = select_default()(fakeElement);\n command('copy');\n fakeElement.remove();\n return selectedText;\n};\n/**\n * Copy action wrapper.\n * @param {String|HTMLElement} target\n * @param {Object} options\n * @return {String}\n */\n\n\nvar ClipboardActionCopy = function ClipboardActionCopy(target) {\n var options = arguments.length > 1 && arguments[1] !== undefined ? arguments[1] : {\n container: document.body\n };\n var selectedText = '';\n\n if (typeof target === 'string') {\n selectedText = fakeCopyAction(target, options);\n } else if (target instanceof HTMLInputElement && !['text', 'search', 'url', 'tel', 'password'].includes(target === null || target === void 0 ? void 0 : target.type)) {\n // If input type doesn't support `setSelectionRange`. Simulate it. https://developer.mozilla.org/en-US/docs/Web/API/HTMLInputElement/setSelectionRange\n selectedText = fakeCopyAction(target.value, options);\n } else {\n selectedText = select_default()(target);\n command('copy');\n }\n\n return selectedText;\n};\n\n/* harmony default export */ var actions_copy = (ClipboardActionCopy);\n;// CONCATENATED MODULE: ./src/actions/default.js\nfunction _typeof(obj) { \"@babel/helpers - typeof\"; if (typeof Symbol === \"function\" && typeof Symbol.iterator === \"symbol\") { _typeof = function _typeof(obj) { return typeof obj; }; } else { _typeof = function _typeof(obj) { return obj && typeof Symbol === \"function\" && obj.constructor === Symbol && obj !== Symbol.prototype ? \"symbol\" : typeof obj; }; } return _typeof(obj); }\n\n\n\n/**\n * Inner function which performs selection from either `text` or `target`\n * properties and then executes copy or cut operations.\n * @param {Object} options\n */\n\nvar ClipboardActionDefault = function ClipboardActionDefault() {\n var options = arguments.length > 0 && arguments[0] !== undefined ? arguments[0] : {};\n // Defines base properties passed from constructor.\n var _options$action = options.action,\n action = _options$action === void 0 ? 'copy' : _options$action,\n container = options.container,\n target = options.target,\n text = options.text; // Sets the `action` to be performed which can be either 'copy' or 'cut'.\n\n if (action !== 'copy' && action !== 'cut') {\n throw new Error('Invalid \"action\" value, use either \"copy\" or \"cut\"');\n } // Sets the `target` property using an element that will be have its content copied.\n\n\n if (target !== undefined) {\n if (target && _typeof(target) === 'object' && target.nodeType === 1) {\n if (action === 'copy' && target.hasAttribute('disabled')) {\n throw new Error('Invalid \"target\" attribute. Please use \"readonly\" instead of \"disabled\" attribute');\n }\n\n if (action === 'cut' && (target.hasAttribute('readonly') || target.hasAttribute('disabled'))) {\n throw new Error('Invalid \"target\" attribute. You can\\'t cut text from elements with \"readonly\" or \"disabled\" attributes');\n }\n } else {\n throw new Error('Invalid \"target\" value, use a valid Element');\n }\n } // Define selection strategy based on `text` property.\n\n\n if (text) {\n return actions_copy(text, {\n container: container\n });\n } // Defines which selection strategy based on `target` property.\n\n\n if (target) {\n return action === 'cut' ? actions_cut(target) : actions_copy(target, {\n container: container\n });\n }\n};\n\n/* harmony default export */ var actions_default = (ClipboardActionDefault);\n;// CONCATENATED MODULE: ./src/clipboard.js\nfunction clipboard_typeof(obj) { \"@babel/helpers - typeof\"; if (typeof Symbol === \"function\" && typeof Symbol.iterator === \"symbol\") { clipboard_typeof = function _typeof(obj) { return typeof obj; }; } else { clipboard_typeof = function _typeof(obj) { return obj && typeof Symbol === \"function\" && obj.constructor === Symbol && obj !== Symbol.prototype ? \"symbol\" : typeof obj; }; } return clipboard_typeof(obj); }\n\nfunction _classCallCheck(instance, Constructor) { if (!(instance instanceof Constructor)) { throw new TypeError(\"Cannot call a class as a function\"); } }\n\nfunction _defineProperties(target, props) { for (var i = 0; i < props.length; i++) { var descriptor = props[i]; descriptor.enumerable = descriptor.enumerable || false; descriptor.configurable = true; if (\"value\" in descriptor) descriptor.writable = true; Object.defineProperty(target, descriptor.key, descriptor); } }\n\nfunction _createClass(Constructor, protoProps, staticProps) { if (protoProps) _defineProperties(Constructor.prototype, protoProps); if (staticProps) _defineProperties(Constructor, staticProps); return Constructor; }\n\nfunction _inherits(subClass, superClass) { if (typeof superClass !== \"function\" && superClass !== null) { throw new TypeError(\"Super expression must either be null or a function\"); } subClass.prototype = Object.create(superClass && superClass.prototype, { constructor: { value: subClass, writable: true, configurable: true } }); if (superClass) _setPrototypeOf(subClass, superClass); }\n\nfunction _setPrototypeOf(o, p) { _setPrototypeOf = Object.setPrototypeOf || function _setPrototypeOf(o, p) { o.__proto__ = p; return o; }; return _setPrototypeOf(o, p); }\n\nfunction _createSuper(Derived) { var hasNativeReflectConstruct = _isNativeReflectConstruct(); return function _createSuperInternal() { var Super = _getPrototypeOf(Derived), result; if (hasNativeReflectConstruct) { var NewTarget = _getPrototypeOf(this).constructor; result = Reflect.construct(Super, arguments, NewTarget); } else { result = Super.apply(this, arguments); } return _possibleConstructorReturn(this, result); }; }\n\nfunction _possibleConstructorReturn(self, call) { if (call && (clipboard_typeof(call) === \"object\" || typeof call === \"function\")) { return call; } return _assertThisInitialized(self); }\n\nfunction _assertThisInitialized(self) { if (self === void 0) { throw new ReferenceError(\"this hasn't been initialised - super() hasn't been called\"); } return self; }\n\nfunction _isNativeReflectConstruct() { if (typeof Reflect === \"undefined\" || !Reflect.construct) return false; if (Reflect.construct.sham) return false; if (typeof Proxy === \"function\") return true; try { Date.prototype.toString.call(Reflect.construct(Date, [], function () {})); return true; } catch (e) { return false; } }\n\nfunction _getPrototypeOf(o) { _getPrototypeOf = Object.setPrototypeOf ? Object.getPrototypeOf : function _getPrototypeOf(o) { return o.__proto__ || Object.getPrototypeOf(o); }; return _getPrototypeOf(o); }\n\n\n\n\n\n\n/**\n * Helper function to retrieve attribute value.\n * @param {String} suffix\n * @param {Element} element\n */\n\nfunction getAttributeValue(suffix, element) {\n var attribute = \"data-clipboard-\".concat(suffix);\n\n if (!element.hasAttribute(attribute)) {\n return;\n }\n\n return element.getAttribute(attribute);\n}\n/**\n * Base class which takes one or more elements, adds event listeners to them,\n * and instantiates a new `ClipboardAction` on each click.\n */\n\n\nvar Clipboard = /*#__PURE__*/function (_Emitter) {\n _inherits(Clipboard, _Emitter);\n\n var _super = _createSuper(Clipboard);\n\n /**\n * @param {String|HTMLElement|HTMLCollection|NodeList} trigger\n * @param {Object} options\n */\n function Clipboard(trigger, options) {\n var _this;\n\n _classCallCheck(this, Clipboard);\n\n _this = _super.call(this);\n\n _this.resolveOptions(options);\n\n _this.listenClick(trigger);\n\n return _this;\n }\n /**\n * Defines if attributes would be resolved using internal setter functions\n * or custom functions that were passed in the constructor.\n * @param {Object} options\n */\n\n\n _createClass(Clipboard, [{\n key: \"resolveOptions\",\n value: function resolveOptions() {\n var options = arguments.length > 0 && arguments[0] !== undefined ? arguments[0] : {};\n this.action = typeof options.action === 'function' ? options.action : this.defaultAction;\n this.target = typeof options.target === 'function' ? options.target : this.defaultTarget;\n this.text = typeof options.text === 'function' ? options.text : this.defaultText;\n this.container = clipboard_typeof(options.container) === 'object' ? options.container : document.body;\n }\n /**\n * Adds a click event listener to the passed trigger.\n * @param {String|HTMLElement|HTMLCollection|NodeList} trigger\n */\n\n }, {\n key: \"listenClick\",\n value: function listenClick(trigger) {\n var _this2 = this;\n\n this.listener = listen_default()(trigger, 'click', function (e) {\n return _this2.onClick(e);\n });\n }\n /**\n * Defines a new `ClipboardAction` on each click event.\n * @param {Event} e\n */\n\n }, {\n key: \"onClick\",\n value: function onClick(e) {\n var trigger = e.delegateTarget || e.currentTarget;\n var action = this.action(trigger) || 'copy';\n var text = actions_default({\n action: action,\n container: this.container,\n target: this.target(trigger),\n text: this.text(trigger)\n }); // Fires an event based on the copy operation result.\n\n this.emit(text ? 'success' : 'error', {\n action: action,\n text: text,\n trigger: trigger,\n clearSelection: function clearSelection() {\n if (trigger) {\n trigger.focus();\n }\n\n window.getSelection().removeAllRanges();\n }\n });\n }\n /**\n * Default `action` lookup function.\n * @param {Element} trigger\n */\n\n }, {\n key: \"defaultAction\",\n value: function defaultAction(trigger) {\n return getAttributeValue('action', trigger);\n }\n /**\n * Default `target` lookup function.\n * @param {Element} trigger\n */\n\n }, {\n key: \"defaultTarget\",\n value: function defaultTarget(trigger) {\n var selector = getAttributeValue('target', trigger);\n\n if (selector) {\n return document.querySelector(selector);\n }\n }\n /**\n * Allow fire programmatically a copy action\n * @param {String|HTMLElement} target\n * @param {Object} options\n * @returns Text copied.\n */\n\n }, {\n key: \"defaultText\",\n\n /**\n * Default `text` lookup function.\n * @param {Element} trigger\n */\n value: function defaultText(trigger) {\n return getAttributeValue('text', trigger);\n }\n /**\n * Destroy lifecycle.\n */\n\n }, {\n key: \"destroy\",\n value: function destroy() {\n this.listener.destroy();\n }\n }], [{\n key: \"copy\",\n value: function copy(target) {\n var options = arguments.length > 1 && arguments[1] !== undefined ? arguments[1] : {\n container: document.body\n };\n return actions_copy(target, options);\n }\n /**\n * Allow fire programmatically a cut action\n * @param {String|HTMLElement} target\n * @returns Text cutted.\n */\n\n }, {\n key: \"cut\",\n value: function cut(target) {\n return actions_cut(target);\n }\n /**\n * Returns the support of the given action, or all actions if no action is\n * given.\n * @param {String} [action]\n */\n\n }, {\n key: \"isSupported\",\n value: function isSupported() {\n var action = arguments.length > 0 && arguments[0] !== undefined ? arguments[0] : ['copy', 'cut'];\n var actions = typeof action === 'string' ? [action] : action;\n var support = !!document.queryCommandSupported;\n actions.forEach(function (action) {\n support = support && !!document.queryCommandSupported(action);\n });\n return support;\n }\n }]);\n\n return Clipboard;\n}((tiny_emitter_default()));\n\n/* harmony default export */ var clipboard = (Clipboard);\n\n/***/ }),\n\n/***/ 828:\n/***/ (function(module) {\n\nvar DOCUMENT_NODE_TYPE = 9;\n\n/**\n * A polyfill for Element.matches()\n */\nif (typeof Element !== 'undefined' && !Element.prototype.matches) {\n var proto = Element.prototype;\n\n proto.matches = proto.matchesSelector ||\n proto.mozMatchesSelector ||\n proto.msMatchesSelector ||\n proto.oMatchesSelector ||\n proto.webkitMatchesSelector;\n}\n\n/**\n * Finds the closest parent that matches a selector.\n *\n * @param {Element} element\n * @param {String} selector\n * @return {Function}\n */\nfunction closest (element, selector) {\n while (element && element.nodeType !== DOCUMENT_NODE_TYPE) {\n if (typeof element.matches === 'function' &&\n element.matches(selector)) {\n return element;\n }\n element = element.parentNode;\n }\n}\n\nmodule.exports = closest;\n\n\n/***/ }),\n\n/***/ 438:\n/***/ (function(module, __unused_webpack_exports, __webpack_require__) {\n\nvar closest = __webpack_require__(828);\n\n/**\n * Delegates event to a selector.\n *\n * @param {Element} element\n * @param {String} selector\n * @param {String} type\n * @param {Function} callback\n * @param {Boolean} useCapture\n * @return {Object}\n */\nfunction _delegate(element, selector, type, callback, useCapture) {\n var listenerFn = listener.apply(this, arguments);\n\n element.addEventListener(type, listenerFn, useCapture);\n\n return {\n destroy: function() {\n element.removeEventListener(type, listenerFn, useCapture);\n }\n }\n}\n\n/**\n * Delegates event to a selector.\n *\n * @param {Element|String|Array} [elements]\n * @param {String} selector\n * @param {String} type\n * @param {Function} callback\n * @param {Boolean} useCapture\n * @return {Object}\n */\nfunction delegate(elements, selector, type, callback, useCapture) {\n // Handle the regular Element usage\n if (typeof elements.addEventListener === 'function') {\n return _delegate.apply(null, arguments);\n }\n\n // Handle Element-less usage, it defaults to global delegation\n if (typeof type === 'function') {\n // Use `document` as the first parameter, then apply arguments\n // This is a short way to .unshift `arguments` without running into deoptimizations\n return _delegate.bind(null, document).apply(null, arguments);\n }\n\n // Handle Selector-based usage\n if (typeof elements === 'string') {\n elements = document.querySelectorAll(elements);\n }\n\n // Handle Array-like based usage\n return Array.prototype.map.call(elements, function (element) {\n return _delegate(element, selector, type, callback, useCapture);\n });\n}\n\n/**\n * Finds closest match and invokes callback.\n *\n * @param {Element} element\n * @param {String} selector\n * @param {String} type\n * @param {Function} callback\n * @return {Function}\n */\nfunction listener(element, selector, type, callback) {\n return function(e) {\n e.delegateTarget = closest(e.target, selector);\n\n if (e.delegateTarget) {\n callback.call(element, e);\n }\n }\n}\n\nmodule.exports = delegate;\n\n\n/***/ }),\n\n/***/ 879:\n/***/ (function(__unused_webpack_module, exports) {\n\n/**\n * Check if argument is a HTML element.\n *\n * @param {Object} value\n * @return {Boolean}\n */\nexports.node = function(value) {\n return value !== undefined\n && value instanceof HTMLElement\n && value.nodeType === 1;\n};\n\n/**\n * Check if argument is a list of HTML elements.\n *\n * @param {Object} value\n * @return {Boolean}\n */\nexports.nodeList = function(value) {\n var type = Object.prototype.toString.call(value);\n\n return value !== undefined\n && (type === '[object NodeList]' || type === '[object HTMLCollection]')\n && ('length' in value)\n && (value.length === 0 || exports.node(value[0]));\n};\n\n/**\n * Check if argument is a string.\n *\n * @param {Object} value\n * @return {Boolean}\n */\nexports.string = function(value) {\n return typeof value === 'string'\n || value instanceof String;\n};\n\n/**\n * Check if argument is a function.\n *\n * @param {Object} value\n * @return {Boolean}\n */\nexports.fn = function(value) {\n var type = Object.prototype.toString.call(value);\n\n return type === '[object Function]';\n};\n\n\n/***/ }),\n\n/***/ 370:\n/***/ (function(module, __unused_webpack_exports, __webpack_require__) {\n\nvar is = __webpack_require__(879);\nvar delegate = __webpack_require__(438);\n\n/**\n * Validates all params and calls the right\n * listener function based on its target type.\n *\n * @param {String|HTMLElement|HTMLCollection|NodeList} target\n * @param {String} type\n * @param {Function} callback\n * @return {Object}\n */\nfunction listen(target, type, callback) {\n if (!target && !type && !callback) {\n throw new Error('Missing required arguments');\n }\n\n if (!is.string(type)) {\n throw new TypeError('Second argument must be a String');\n }\n\n if (!is.fn(callback)) {\n throw new TypeError('Third argument must be a Function');\n }\n\n if (is.node(target)) {\n return listenNode(target, type, callback);\n }\n else if (is.nodeList(target)) {\n return listenNodeList(target, type, callback);\n }\n else if (is.string(target)) {\n return listenSelector(target, type, callback);\n }\n else {\n throw new TypeError('First argument must be a String, HTMLElement, HTMLCollection, or NodeList');\n }\n}\n\n/**\n * Adds an event listener to a HTML element\n * and returns a remove listener function.\n *\n * @param {HTMLElement} node\n * @param {String} type\n * @param {Function} callback\n * @return {Object}\n */\nfunction listenNode(node, type, callback) {\n node.addEventListener(type, callback);\n\n return {\n destroy: function() {\n node.removeEventListener(type, callback);\n }\n }\n}\n\n/**\n * Add an event listener to a list of HTML elements\n * and returns a remove listener function.\n *\n * @param {NodeList|HTMLCollection} nodeList\n * @param {String} type\n * @param {Function} callback\n * @return {Object}\n */\nfunction listenNodeList(nodeList, type, callback) {\n Array.prototype.forEach.call(nodeList, function(node) {\n node.addEventListener(type, callback);\n });\n\n return {\n destroy: function() {\n Array.prototype.forEach.call(nodeList, function(node) {\n node.removeEventListener(type, callback);\n });\n }\n }\n}\n\n/**\n * Add an event listener to a selector\n * and returns a remove listener function.\n *\n * @param {String} selector\n * @param {String} type\n * @param {Function} callback\n * @return {Object}\n */\nfunction listenSelector(selector, type, callback) {\n return delegate(document.body, selector, type, callback);\n}\n\nmodule.exports = listen;\n\n\n/***/ }),\n\n/***/ 817:\n/***/ (function(module) {\n\nfunction select(element) {\n var selectedText;\n\n if (element.nodeName === 'SELECT') {\n element.focus();\n\n selectedText = element.value;\n }\n else if (element.nodeName === 'INPUT' || element.nodeName === 'TEXTAREA') {\n var isReadOnly = element.hasAttribute('readonly');\n\n if (!isReadOnly) {\n element.setAttribute('readonly', '');\n }\n\n element.select();\n element.setSelectionRange(0, element.value.length);\n\n if (!isReadOnly) {\n element.removeAttribute('readonly');\n }\n\n selectedText = element.value;\n }\n else {\n if (element.hasAttribute('contenteditable')) {\n element.focus();\n }\n\n var selection = window.getSelection();\n var range = document.createRange();\n\n range.selectNodeContents(element);\n selection.removeAllRanges();\n selection.addRange(range);\n\n selectedText = selection.toString();\n }\n\n return selectedText;\n}\n\nmodule.exports = select;\n\n\n/***/ }),\n\n/***/ 279:\n/***/ (function(module) {\n\nfunction E () {\n // Keep this empty so it's easier to inherit from\n // (via https://github.com/lipsmack from https://github.com/scottcorgan/tiny-emitter/issues/3)\n}\n\nE.prototype = {\n on: function (name, callback, ctx) {\n var e = this.e || (this.e = {});\n\n (e[name] || (e[name] = [])).push({\n fn: callback,\n ctx: ctx\n });\n\n return this;\n },\n\n once: function (name, callback, ctx) {\n var self = this;\n function listener () {\n self.off(name, listener);\n callback.apply(ctx, arguments);\n };\n\n listener._ = callback\n return this.on(name, listener, ctx);\n },\n\n emit: function (name) {\n var data = [].slice.call(arguments, 1);\n var evtArr = ((this.e || (this.e = {}))[name] || []).slice();\n var i = 0;\n var len = evtArr.length;\n\n for (i; i < len; i++) {\n evtArr[i].fn.apply(evtArr[i].ctx, data);\n }\n\n return this;\n },\n\n off: function (name, callback) {\n var e = this.e || (this.e = {});\n var evts = e[name];\n var liveEvents = [];\n\n if (evts && callback) {\n for (var i = 0, len = evts.length; i < len; i++) {\n if (evts[i].fn !== callback && evts[i].fn._ !== callback)\n liveEvents.push(evts[i]);\n }\n }\n\n // Remove event from queue to prevent memory leak\n // Suggested by https://github.com/lazd\n // Ref: https://github.com/scottcorgan/tiny-emitter/commit/c6ebfaa9bc973b33d110a84a307742b7cf94c953#commitcomment-5024910\n\n (liveEvents.length)\n ? e[name] = liveEvents\n : delete e[name];\n\n return this;\n }\n};\n\nmodule.exports = E;\nmodule.exports.TinyEmitter = E;\n\n\n/***/ })\n\n/******/ \t});\n/************************************************************************/\n/******/ \t// The module cache\n/******/ \tvar __webpack_module_cache__ = {};\n/******/ \t\n/******/ \t// The require function\n/******/ \tfunction __webpack_require__(moduleId) {\n/******/ \t\t// Check if module is in cache\n/******/ \t\tif(__webpack_module_cache__[moduleId]) {\n/******/ \t\t\treturn __webpack_module_cache__[moduleId].exports;\n/******/ \t\t}\n/******/ \t\t// Create a new module (and put it into the cache)\n/******/ \t\tvar module = __webpack_module_cache__[moduleId] = {\n/******/ \t\t\t// no module.id needed\n/******/ \t\t\t// no module.loaded needed\n/******/ \t\t\texports: {}\n/******/ \t\t};\n/******/ \t\n/******/ \t\t// Execute the module function\n/******/ \t\t__webpack_modules__[moduleId](module, module.exports, __webpack_require__);\n/******/ \t\n/******/ \t\t// Return the exports of the module\n/******/ \t\treturn module.exports;\n/******/ \t}\n/******/ \t\n/************************************************************************/\n/******/ \t/* webpack/runtime/compat get default export */\n/******/ \t!function() {\n/******/ \t\t// getDefaultExport function for compatibility with non-harmony modules\n/******/ \t\t__webpack_require__.n = function(module) {\n/******/ \t\t\tvar getter = module && module.__esModule ?\n/******/ \t\t\t\tfunction() { return module['default']; } :\n/******/ \t\t\t\tfunction() { return module; };\n/******/ \t\t\t__webpack_require__.d(getter, { a: getter });\n/******/ \t\t\treturn getter;\n/******/ \t\t};\n/******/ \t}();\n/******/ \t\n/******/ \t/* webpack/runtime/define property getters */\n/******/ \t!function() {\n/******/ \t\t// define getter functions for harmony exports\n/******/ \t\t__webpack_require__.d = function(exports, definition) {\n/******/ \t\t\tfor(var key in definition) {\n/******/ \t\t\t\tif(__webpack_require__.o(definition, key) && !__webpack_require__.o(exports, key)) {\n/******/ \t\t\t\t\tObject.defineProperty(exports, key, { enumerable: true, get: definition[key] });\n/******/ \t\t\t\t}\n/******/ \t\t\t}\n/******/ \t\t};\n/******/ \t}();\n/******/ \t\n/******/ \t/* webpack/runtime/hasOwnProperty shorthand */\n/******/ \t!function() {\n/******/ \t\t__webpack_require__.o = function(obj, prop) { return Object.prototype.hasOwnProperty.call(obj, prop); }\n/******/ \t}();\n/******/ \t\n/************************************************************************/\n/******/ \t// module exports must be returned from runtime so entry inlining is disabled\n/******/ \t// startup\n/******/ \t// Load entry module and return exports\n/******/ \treturn __webpack_require__(686);\n/******/ })()\n.default;\n});", "/*!\n * escape-html\n * Copyright(c) 2012-2013 TJ Holowaychuk\n * Copyright(c) 2015 Andreas Lubbe\n * Copyright(c) 2015 Tiancheng \"Timothy\" Gu\n * MIT Licensed\n */\n\n'use strict';\n\n/**\n * Module variables.\n * @private\n */\n\nvar matchHtmlRegExp = /[\"'&<>]/;\n\n/**\n * Module exports.\n * @public\n */\n\nmodule.exports = escapeHtml;\n\n/**\n * Escape special characters in the given string of html.\n *\n * @param {string} string The string to escape for inserting into HTML\n * @return {string}\n * @public\n */\n\nfunction escapeHtml(string) {\n var str = '' + string;\n var match = matchHtmlRegExp.exec(str);\n\n if (!match) {\n return str;\n }\n\n var escape;\n var html = '';\n var index = 0;\n var lastIndex = 0;\n\n for (index = match.index; index < str.length; index++) {\n switch (str.charCodeAt(index)) {\n case 34: // \"\n escape = '"';\n break;\n case 38: // &\n escape = '&';\n break;\n case 39: // '\n escape = ''';\n break;\n case 60: // <\n escape = '<';\n break;\n case 62: // >\n escape = '>';\n break;\n default:\n continue;\n }\n\n if (lastIndex !== index) {\n html += str.substring(lastIndex, index);\n }\n\n lastIndex = index + 1;\n html += escape;\n }\n\n return lastIndex !== index\n ? html + str.substring(lastIndex, index)\n : html;\n}\n", "/*\n * Copyright (c) 2016-2023 Martin Donath \n *\n * Permission is hereby granted, free of charge, to any person obtaining a copy\n * of this software and associated documentation files (the \"Software\"), to\n * deal in the Software without restriction, including without limitation the\n * rights to use, copy, modify, merge, publish, distribute, sublicense, and/or\n * sell copies of the Software, and to permit persons to whom the Software is\n * furnished to do so, subject to the following conditions:\n *\n * The above copyright notice and this permission notice shall be included in\n * all copies or substantial portions of the Software.\n *\n * THE SOFTWARE IS PROVIDED \"AS IS\", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR\n * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,\n * FITNESS FOR A PARTICULAR PURPOSE AND NON-INFRINGEMENT. IN NO EVENT SHALL THE\n * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER\n * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING\n * FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS\n * IN THE SOFTWARE.\n */\n\nimport \"focus-visible\"\n\nimport {\n EMPTY,\n NEVER,\n Observable,\n Subject,\n defer,\n delay,\n filter,\n map,\n merge,\n mergeWith,\n shareReplay,\n switchMap\n} from \"rxjs\"\n\nimport { configuration, feature } from \"./_\"\nimport {\n at,\n getActiveElement,\n getOptionalElement,\n requestJSON,\n setLocation,\n setToggle,\n watchDocument,\n watchKeyboard,\n watchLocation,\n watchLocationTarget,\n watchMedia,\n watchPrint,\n watchScript,\n watchViewport\n} from \"./browser\"\nimport {\n getComponentElement,\n getComponentElements,\n mountAnnounce,\n mountBackToTop,\n mountConsent,\n mountContent,\n mountDialog,\n mountHeader,\n mountHeaderTitle,\n mountPalette,\n mountProgress,\n mountSearch,\n mountSearchHiglight,\n mountSidebar,\n mountSource,\n mountTableOfContents,\n mountTabs,\n watchHeader,\n watchMain\n} from \"./components\"\nimport {\n SearchIndex,\n setupClipboardJS,\n setupInstantNavigation,\n setupVersionSelector\n} from \"./integrations\"\nimport {\n patchIndeterminate,\n patchScrollfix,\n patchScrolllock\n} from \"./patches\"\nimport \"./polyfills\"\n\n/* ----------------------------------------------------------------------------\n * Functions - @todo refactor\n * ------------------------------------------------------------------------- */\n\n/**\n * Fetch search index\n *\n * @returns Search index observable\n */\nfunction fetchSearchIndex(): Observable {\n if (location.protocol === \"file:\") {\n return watchScript(\n `${new URL(\"search/search_index.js\", config.base)}`\n )\n .pipe(\n // @ts-ignore - @todo fix typings\n map(() => __index),\n shareReplay(1)\n )\n } else {\n return requestJSON(\n new URL(\"search/search_index.json\", config.base)\n )\n }\n}\n\n/* ----------------------------------------------------------------------------\n * Application\n * ------------------------------------------------------------------------- */\n\n/* Yay, JavaScript is available */\ndocument.documentElement.classList.remove(\"no-js\")\ndocument.documentElement.classList.add(\"js\")\n\n/* Set up navigation observables and subjects */\nconst document$ = watchDocument()\nconst location$ = watchLocation()\nconst target$ = watchLocationTarget(location$)\nconst keyboard$ = watchKeyboard()\n\n/* Set up media observables */\nconst viewport$ = watchViewport()\nconst tablet$ = watchMedia(\"(min-width: 960px)\")\nconst screen$ = watchMedia(\"(min-width: 1220px)\")\nconst print$ = watchPrint()\n\n/* Retrieve search index, if search is enabled */\nconst config = configuration()\nconst index$ = document.forms.namedItem(\"search\")\n ? fetchSearchIndex()\n : NEVER\n\n/* Set up Clipboard.js integration */\nconst alert$ = new Subject()\nsetupClipboardJS({ alert$ })\n\n/* Set up progress indicator */\nconst progress$ = new Subject()\n\n/* Set up instant navigation, if enabled */\nif (feature(\"navigation.instant\"))\n setupInstantNavigation({ location$, viewport$, progress$ })\n .subscribe(document$)\n\n/* Set up version selector */\nif (config.version?.provider === \"mike\")\n setupVersionSelector({ document$ })\n\n/* Always close drawer and search on navigation */\nmerge(location$, target$)\n .pipe(\n delay(125)\n )\n .subscribe(() => {\n setToggle(\"drawer\", false)\n setToggle(\"search\", false)\n })\n\n/* Set up global keyboard handlers */\nkeyboard$\n .pipe(\n filter(({ mode }) => mode === \"global\")\n )\n .subscribe(key => {\n switch (key.type) {\n\n /* Go to previous page */\n case \"p\":\n case \",\":\n const prev = getOptionalElement(\"link[rel=prev]\")\n if (typeof prev !== \"undefined\")\n setLocation(prev)\n break\n\n /* Go to next page */\n case \"n\":\n case \".\":\n const next = getOptionalElement(\"link[rel=next]\")\n if (typeof next !== \"undefined\")\n setLocation(next)\n break\n\n /* Expand navigation, see https://bit.ly/3ZjG5io */\n case \"Enter\":\n const active = getActiveElement()\n if (active instanceof HTMLLabelElement)\n active.click()\n }\n })\n\n/* Set up patches */\npatchIndeterminate({ document$, tablet$ })\npatchScrollfix({ document$ })\npatchScrolllock({ viewport$, tablet$ })\n\n/* Set up header and main area observable */\nconst header$ = watchHeader(getComponentElement(\"header\"), { viewport$ })\nconst main$ = document$\n .pipe(\n map(() => getComponentElement(\"main\")),\n switchMap(el => watchMain(el, { viewport$, header$ })),\n shareReplay(1)\n )\n\n/* Set up control component observables */\nconst control$ = merge(\n\n /* Consent */\n ...getComponentElements(\"consent\")\n .map(el => mountConsent(el, { target$ })),\n\n /* Dialog */\n ...getComponentElements(\"dialog\")\n .map(el => mountDialog(el, { alert$ })),\n\n /* Header */\n ...getComponentElements(\"header\")\n .map(el => mountHeader(el, { viewport$, header$, main$ })),\n\n /* Color palette */\n ...getComponentElements(\"palette\")\n .map(el => mountPalette(el)),\n\n /* Progress bar */\n ...getComponentElements(\"progress\")\n .map(el => mountProgress(el, { progress$ })),\n\n /* Search */\n ...getComponentElements(\"search\")\n .map(el => mountSearch(el, { index$, keyboard$ })),\n\n /* Repository information */\n ...getComponentElements(\"source\")\n .map(el => mountSource(el))\n)\n\n/* Set up content component observables */\nconst content$ = defer(() => merge(\n\n /* Announcement bar */\n ...getComponentElements(\"announce\")\n .map(el => mountAnnounce(el)),\n\n /* Content */\n ...getComponentElements(\"content\")\n .map(el => mountContent(el, { viewport$, target$, print$ })),\n\n /* Search highlighting */\n ...getComponentElements(\"content\")\n .map(el => feature(\"search.highlight\")\n ? mountSearchHiglight(el, { index$, location$ })\n : EMPTY\n ),\n\n /* Header title */\n ...getComponentElements(\"header-title\")\n .map(el => mountHeaderTitle(el, { viewport$, header$ })),\n\n /* Sidebar */\n ...getComponentElements(\"sidebar\")\n .map(el => el.getAttribute(\"data-md-type\") === \"navigation\"\n ? at(screen$, () => mountSidebar(el, { viewport$, header$, main$ }))\n : at(tablet$, () => mountSidebar(el, { viewport$, header$, main$ }))\n ),\n\n /* Navigation tabs */\n ...getComponentElements(\"tabs\")\n .map(el => mountTabs(el, { viewport$, header$ })),\n\n /* Table of contents */\n ...getComponentElements(\"toc\")\n .map(el => mountTableOfContents(el, {\n viewport$, header$, main$, target$\n })),\n\n /* Back-to-top button */\n ...getComponentElements(\"top\")\n .map(el => mountBackToTop(el, { viewport$, header$, main$, target$ }))\n))\n\n/* Set up component observables */\nconst component$ = document$\n .pipe(\n switchMap(() => content$),\n mergeWith(control$),\n shareReplay(1)\n )\n\n/* Subscribe to all components */\ncomponent$.subscribe()\n\n/* ----------------------------------------------------------------------------\n * Exports\n * ------------------------------------------------------------------------- */\n\nwindow.document$ = document$ /* Document observable */\nwindow.location$ = location$ /* Location subject */\nwindow.target$ = target$ /* Location target observable */\nwindow.keyboard$ = keyboard$ /* Keyboard observable */\nwindow.viewport$ = viewport$ /* Viewport observable */\nwindow.tablet$ = tablet$ /* Media tablet observable */\nwindow.screen$ = screen$ /* Media screen observable */\nwindow.print$ = print$ /* Media print observable */\nwindow.alert$ = alert$ /* Alert subject */\nwindow.progress$ = progress$ /* Progress indicator subject */\nwindow.component$ = component$ /* Component observable */\n", "/*! *****************************************************************************\r\nCopyright (c) Microsoft Corporation.\r\n\r\nPermission to use, copy, modify, and/or distribute this software for any\r\npurpose with or without fee is hereby granted.\r\n\r\nTHE SOFTWARE IS PROVIDED \"AS IS\" AND THE AUTHOR DISCLAIMS ALL WARRANTIES WITH\r\nREGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF MERCHANTABILITY\r\nAND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY SPECIAL, DIRECT,\r\nINDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES WHATSOEVER RESULTING FROM\r\nLOSS OF USE, DATA OR PROFITS, WHETHER IN AN ACTION OF CONTRACT, NEGLIGENCE OR\r\nOTHER TORTIOUS ACTION, ARISING OUT OF OR IN CONNECTION WITH THE USE OR\r\nPERFORMANCE OF THIS SOFTWARE.\r\n***************************************************************************** */\r\n/* global Reflect, Promise */\r\n\r\nvar extendStatics = function(d, b) {\r\n extendStatics = Object.setPrototypeOf ||\r\n ({ __proto__: [] } instanceof Array && function (d, b) { d.__proto__ = b; }) ||\r\n function (d, b) { for (var p in b) if (Object.prototype.hasOwnProperty.call(b, p)) d[p] = b[p]; };\r\n return extendStatics(d, b);\r\n};\r\n\r\nexport function __extends(d, b) {\r\n if (typeof b !== \"function\" && b !== null)\r\n throw new TypeError(\"Class extends value \" + String(b) + \" is not a constructor or null\");\r\n extendStatics(d, b);\r\n function __() { this.constructor = d; }\r\n d.prototype = b === null ? Object.create(b) : (__.prototype = b.prototype, new __());\r\n}\r\n\r\nexport var __assign = function() {\r\n __assign = Object.assign || function __assign(t) {\r\n for (var s, i = 1, n = arguments.length; i < n; i++) {\r\n s = arguments[i];\r\n for (var p in s) if (Object.prototype.hasOwnProperty.call(s, p)) t[p] = s[p];\r\n }\r\n return t;\r\n }\r\n return __assign.apply(this, arguments);\r\n}\r\n\r\nexport function __rest(s, e) {\r\n var t = {};\r\n for (var p in s) if (Object.prototype.hasOwnProperty.call(s, p) && e.indexOf(p) < 0)\r\n t[p] = s[p];\r\n if (s != null && typeof Object.getOwnPropertySymbols === \"function\")\r\n for (var i = 0, p = Object.getOwnPropertySymbols(s); i < p.length; i++) {\r\n if (e.indexOf(p[i]) < 0 && Object.prototype.propertyIsEnumerable.call(s, p[i]))\r\n t[p[i]] = s[p[i]];\r\n }\r\n return t;\r\n}\r\n\r\nexport function __decorate(decorators, target, key, desc) {\r\n var c = arguments.length, r = c < 3 ? target : desc === null ? desc = Object.getOwnPropertyDescriptor(target, key) : desc, d;\r\n if (typeof Reflect === \"object\" && typeof Reflect.decorate === \"function\") r = Reflect.decorate(decorators, target, key, desc);\r\n else for (var i = decorators.length - 1; i >= 0; i--) if (d = decorators[i]) r = (c < 3 ? d(r) : c > 3 ? d(target, key, r) : d(target, key)) || r;\r\n return c > 3 && r && Object.defineProperty(target, key, r), r;\r\n}\r\n\r\nexport function __param(paramIndex, decorator) {\r\n return function (target, key) { decorator(target, key, paramIndex); }\r\n}\r\n\r\nexport function __metadata(metadataKey, metadataValue) {\r\n if (typeof Reflect === \"object\" && typeof Reflect.metadata === \"function\") return Reflect.metadata(metadataKey, metadataValue);\r\n}\r\n\r\nexport function __awaiter(thisArg, _arguments, P, generator) {\r\n function adopt(value) { return value instanceof P ? value : new P(function (resolve) { resolve(value); }); }\r\n return new (P || (P = Promise))(function (resolve, reject) {\r\n function fulfilled(value) { try { step(generator.next(value)); } catch (e) { reject(e); } }\r\n function rejected(value) { try { step(generator[\"throw\"](value)); } catch (e) { reject(e); } }\r\n function step(result) { result.done ? resolve(result.value) : adopt(result.value).then(fulfilled, rejected); }\r\n step((generator = generator.apply(thisArg, _arguments || [])).next());\r\n });\r\n}\r\n\r\nexport function __generator(thisArg, body) {\r\n var _ = { label: 0, sent: function() { if (t[0] & 1) throw t[1]; return t[1]; }, trys: [], ops: [] }, f, y, t, g;\r\n return g = { next: verb(0), \"throw\": verb(1), \"return\": verb(2) }, typeof Symbol === \"function\" && (g[Symbol.iterator] = function() { return this; }), g;\r\n function verb(n) { return function (v) { return step([n, v]); }; }\r\n function step(op) {\r\n if (f) throw new TypeError(\"Generator is already executing.\");\r\n while (_) try {\r\n if (f = 1, y && (t = op[0] & 2 ? y[\"return\"] : op[0] ? y[\"throw\"] || ((t = y[\"return\"]) && t.call(y), 0) : y.next) && !(t = t.call(y, op[1])).done) return t;\r\n if (y = 0, t) op = [op[0] & 2, t.value];\r\n switch (op[0]) {\r\n case 0: case 1: t = op; break;\r\n case 4: _.label++; return { value: op[1], done: false };\r\n case 5: _.label++; y = op[1]; op = [0]; continue;\r\n case 7: op = _.ops.pop(); _.trys.pop(); continue;\r\n default:\r\n if (!(t = _.trys, t = t.length > 0 && t[t.length - 1]) && (op[0] === 6 || op[0] === 2)) { _ = 0; continue; }\r\n if (op[0] === 3 && (!t || (op[1] > t[0] && op[1] < t[3]))) { _.label = op[1]; break; }\r\n if (op[0] === 6 && _.label < t[1]) { _.label = t[1]; t = op; break; }\r\n if (t && _.label < t[2]) { _.label = t[2]; _.ops.push(op); break; }\r\n if (t[2]) _.ops.pop();\r\n _.trys.pop(); continue;\r\n }\r\n op = body.call(thisArg, _);\r\n } catch (e) { op = [6, e]; y = 0; } finally { f = t = 0; }\r\n if (op[0] & 5) throw op[1]; return { value: op[0] ? op[1] : void 0, done: true };\r\n }\r\n}\r\n\r\nexport var __createBinding = Object.create ? (function(o, m, k, k2) {\r\n if (k2 === undefined) k2 = k;\r\n Object.defineProperty(o, k2, { enumerable: true, get: function() { return m[k]; } });\r\n}) : (function(o, m, k, k2) {\r\n if (k2 === undefined) k2 = k;\r\n o[k2] = m[k];\r\n});\r\n\r\nexport function __exportStar(m, o) {\r\n for (var p in m) if (p !== \"default\" && !Object.prototype.hasOwnProperty.call(o, p)) __createBinding(o, m, p);\r\n}\r\n\r\nexport function __values(o) {\r\n var s = typeof Symbol === \"function\" && Symbol.iterator, m = s && o[s], i = 0;\r\n if (m) return m.call(o);\r\n if (o && typeof o.length === \"number\") return {\r\n next: function () {\r\n if (o && i >= o.length) o = void 0;\r\n return { value: o && o[i++], done: !o };\r\n }\r\n };\r\n throw new TypeError(s ? \"Object is not iterable.\" : \"Symbol.iterator is not defined.\");\r\n}\r\n\r\nexport function __read(o, n) {\r\n var m = typeof Symbol === \"function\" && o[Symbol.iterator];\r\n if (!m) return o;\r\n var i = m.call(o), r, ar = [], e;\r\n try {\r\n while ((n === void 0 || n-- > 0) && !(r = i.next()).done) ar.push(r.value);\r\n }\r\n catch (error) { e = { error: error }; }\r\n finally {\r\n try {\r\n if (r && !r.done && (m = i[\"return\"])) m.call(i);\r\n }\r\n finally { if (e) throw e.error; }\r\n }\r\n return ar;\r\n}\r\n\r\n/** @deprecated */\r\nexport function __spread() {\r\n for (var ar = [], i = 0; i < arguments.length; i++)\r\n ar = ar.concat(__read(arguments[i]));\r\n return ar;\r\n}\r\n\r\n/** @deprecated */\r\nexport function __spreadArrays() {\r\n for (var s = 0, i = 0, il = arguments.length; i < il; i++) s += arguments[i].length;\r\n for (var r = Array(s), k = 0, i = 0; i < il; i++)\r\n for (var a = arguments[i], j = 0, jl = a.length; j < jl; j++, k++)\r\n r[k] = a[j];\r\n return r;\r\n}\r\n\r\nexport function __spreadArray(to, from, pack) {\r\n if (pack || arguments.length === 2) for (var i = 0, l = from.length, ar; i < l; i++) {\r\n if (ar || !(i in from)) {\r\n if (!ar) ar = Array.prototype.slice.call(from, 0, i);\r\n ar[i] = from[i];\r\n }\r\n }\r\n return to.concat(ar || Array.prototype.slice.call(from));\r\n}\r\n\r\nexport function __await(v) {\r\n return this instanceof __await ? (this.v = v, this) : new __await(v);\r\n}\r\n\r\nexport function __asyncGenerator(thisArg, _arguments, generator) {\r\n if (!Symbol.asyncIterator) throw new TypeError(\"Symbol.asyncIterator is not defined.\");\r\n var g = generator.apply(thisArg, _arguments || []), i, q = [];\r\n return i = {}, verb(\"next\"), verb(\"throw\"), verb(\"return\"), i[Symbol.asyncIterator] = function () { return this; }, i;\r\n function verb(n) { if (g[n]) i[n] = function (v) { return new Promise(function (a, b) { q.push([n, v, a, b]) > 1 || resume(n, v); }); }; }\r\n function resume(n, v) { try { step(g[n](v)); } catch (e) { settle(q[0][3], e); } }\r\n function step(r) { r.value instanceof __await ? Promise.resolve(r.value.v).then(fulfill, reject) : settle(q[0][2], r); }\r\n function fulfill(value) { resume(\"next\", value); }\r\n function reject(value) { resume(\"throw\", value); }\r\n function settle(f, v) { if (f(v), q.shift(), q.length) resume(q[0][0], q[0][1]); }\r\n}\r\n\r\nexport function __asyncDelegator(o) {\r\n var i, p;\r\n return i = {}, verb(\"next\"), verb(\"throw\", function (e) { throw e; }), verb(\"return\"), i[Symbol.iterator] = function () { return this; }, i;\r\n function verb(n, f) { i[n] = o[n] ? function (v) { return (p = !p) ? { value: __await(o[n](v)), done: n === \"return\" } : f ? f(v) : v; } : f; }\r\n}\r\n\r\nexport function __asyncValues(o) {\r\n if (!Symbol.asyncIterator) throw new TypeError(\"Symbol.asyncIterator is not defined.\");\r\n var m = o[Symbol.asyncIterator], i;\r\n return m ? m.call(o) : (o = typeof __values === \"function\" ? __values(o) : o[Symbol.iterator](), i = {}, verb(\"next\"), verb(\"throw\"), verb(\"return\"), i[Symbol.asyncIterator] = function () { return this; }, i);\r\n function verb(n) { i[n] = o[n] && function (v) { return new Promise(function (resolve, reject) { v = o[n](v), settle(resolve, reject, v.done, v.value); }); }; }\r\n function settle(resolve, reject, d, v) { Promise.resolve(v).then(function(v) { resolve({ value: v, done: d }); }, reject); }\r\n}\r\n\r\nexport function __makeTemplateObject(cooked, raw) {\r\n if (Object.defineProperty) { Object.defineProperty(cooked, \"raw\", { value: raw }); } else { cooked.raw = raw; }\r\n return cooked;\r\n};\r\n\r\nvar __setModuleDefault = Object.create ? (function(o, v) {\r\n Object.defineProperty(o, \"default\", { enumerable: true, value: v });\r\n}) : function(o, v) {\r\n o[\"default\"] = v;\r\n};\r\n\r\nexport function __importStar(mod) {\r\n if (mod && mod.__esModule) return mod;\r\n var result = {};\r\n if (mod != null) for (var k in mod) if (k !== \"default\" && Object.prototype.hasOwnProperty.call(mod, k)) __createBinding(result, mod, k);\r\n __setModuleDefault(result, mod);\r\n return result;\r\n}\r\n\r\nexport function __importDefault(mod) {\r\n return (mod && mod.__esModule) ? mod : { default: mod };\r\n}\r\n\r\nexport function __classPrivateFieldGet(receiver, state, kind, f) {\r\n if (kind === \"a\" && !f) throw new TypeError(\"Private accessor was defined without a getter\");\r\n if (typeof state === \"function\" ? receiver !== state || !f : !state.has(receiver)) throw new TypeError(\"Cannot read private member from an object whose class did not declare it\");\r\n return kind === \"m\" ? f : kind === \"a\" ? f.call(receiver) : f ? f.value : state.get(receiver);\r\n}\r\n\r\nexport function __classPrivateFieldSet(receiver, state, value, kind, f) {\r\n if (kind === \"m\") throw new TypeError(\"Private method is not writable\");\r\n if (kind === \"a\" && !f) throw new TypeError(\"Private accessor was defined without a setter\");\r\n if (typeof state === \"function\" ? receiver !== state || !f : !state.has(receiver)) throw new TypeError(\"Cannot write private member to an object whose class did not declare it\");\r\n return (kind === \"a\" ? f.call(receiver, value) : f ? f.value = value : state.set(receiver, value)), value;\r\n}\r\n", "/**\n * Returns true if the object is a function.\n * @param value The value to check\n */\nexport function isFunction(value: any): value is (...args: any[]) => any {\n return typeof value === 'function';\n}\n", "/**\n * Used to create Error subclasses until the community moves away from ES5.\n *\n * This is because compiling from TypeScript down to ES5 has issues with subclassing Errors\n * as well as other built-in types: https://github.com/Microsoft/TypeScript/issues/12123\n *\n * @param createImpl A factory function to create the actual constructor implementation. The returned\n * function should be a named function that calls `_super` internally.\n */\nexport function createErrorClass(createImpl: (_super: any) => any): T {\n const _super = (instance: any) => {\n Error.call(instance);\n instance.stack = new Error().stack;\n };\n\n const ctorFunc = createImpl(_super);\n ctorFunc.prototype = Object.create(Error.prototype);\n ctorFunc.prototype.constructor = ctorFunc;\n return ctorFunc;\n}\n", "import { createErrorClass } from './createErrorClass';\n\nexport interface UnsubscriptionError extends Error {\n readonly errors: any[];\n}\n\nexport interface UnsubscriptionErrorCtor {\n /**\n * @deprecated Internal implementation detail. Do not construct error instances.\n * Cannot be tagged as internal: https://github.com/ReactiveX/rxjs/issues/6269\n */\n new (errors: any[]): UnsubscriptionError;\n}\n\n/**\n * An error thrown when one or more errors have occurred during the\n * `unsubscribe` of a {@link Subscription}.\n */\nexport const UnsubscriptionError: UnsubscriptionErrorCtor = createErrorClass(\n (_super) =>\n function UnsubscriptionErrorImpl(this: any, errors: (Error | string)[]) {\n _super(this);\n this.message = errors\n ? `${errors.length} errors occurred during unsubscription:\n${errors.map((err, i) => `${i + 1}) ${err.toString()}`).join('\\n ')}`\n : '';\n this.name = 'UnsubscriptionError';\n this.errors = errors;\n }\n);\n", "/**\n * Removes an item from an array, mutating it.\n * @param arr The array to remove the item from\n * @param item The item to remove\n */\nexport function arrRemove(arr: T[] | undefined | null, item: T) {\n if (arr) {\n const index = arr.indexOf(item);\n 0 <= index && arr.splice(index, 1);\n }\n}\n", "import { isFunction } from './util/isFunction';\nimport { UnsubscriptionError } from './util/UnsubscriptionError';\nimport { SubscriptionLike, TeardownLogic, Unsubscribable } from './types';\nimport { arrRemove } from './util/arrRemove';\n\n/**\n * Represents a disposable resource, such as the execution of an Observable. A\n * Subscription has one important method, `unsubscribe`, that takes no argument\n * and just disposes the resource held by the subscription.\n *\n * Additionally, subscriptions may be grouped together through the `add()`\n * method, which will attach a child Subscription to the current Subscription.\n * When a Subscription is unsubscribed, all its children (and its grandchildren)\n * will be unsubscribed as well.\n *\n * @class Subscription\n */\nexport class Subscription implements SubscriptionLike {\n /** @nocollapse */\n public static EMPTY = (() => {\n const empty = new Subscription();\n empty.closed = true;\n return empty;\n })();\n\n /**\n * A flag to indicate whether this Subscription has already been unsubscribed.\n */\n public closed = false;\n\n private _parentage: Subscription[] | Subscription | null = null;\n\n /**\n * The list of registered finalizers to execute upon unsubscription. Adding and removing from this\n * list occurs in the {@link #add} and {@link #remove} methods.\n */\n private _finalizers: Exclude[] | null = null;\n\n /**\n * @param initialTeardown A function executed first as part of the finalization\n * process that is kicked off when {@link #unsubscribe} is called.\n */\n constructor(private initialTeardown?: () => void) {}\n\n /**\n * Disposes the resources held by the subscription. May, for instance, cancel\n * an ongoing Observable execution or cancel any other type of work that\n * started when the Subscription was created.\n * @return {void}\n */\n unsubscribe(): void {\n let errors: any[] | undefined;\n\n if (!this.closed) {\n this.closed = true;\n\n // Remove this from it's parents.\n const { _parentage } = this;\n if (_parentage) {\n this._parentage = null;\n if (Array.isArray(_parentage)) {\n for (const parent of _parentage) {\n parent.remove(this);\n }\n } else {\n _parentage.remove(this);\n }\n }\n\n const { initialTeardown: initialFinalizer } = this;\n if (isFunction(initialFinalizer)) {\n try {\n initialFinalizer();\n } catch (e) {\n errors = e instanceof UnsubscriptionError ? e.errors : [e];\n }\n }\n\n const { _finalizers } = this;\n if (_finalizers) {\n this._finalizers = null;\n for (const finalizer of _finalizers) {\n try {\n execFinalizer(finalizer);\n } catch (err) {\n errors = errors ?? [];\n if (err instanceof UnsubscriptionError) {\n errors = [...errors, ...err.errors];\n } else {\n errors.push(err);\n }\n }\n }\n }\n\n if (errors) {\n throw new UnsubscriptionError(errors);\n }\n }\n }\n\n /**\n * Adds a finalizer to this subscription, so that finalization will be unsubscribed/called\n * when this subscription is unsubscribed. If this subscription is already {@link #closed},\n * because it has already been unsubscribed, then whatever finalizer is passed to it\n * will automatically be executed (unless the finalizer itself is also a closed subscription).\n *\n * Closed Subscriptions cannot be added as finalizers to any subscription. Adding a closed\n * subscription to a any subscription will result in no operation. (A noop).\n *\n * Adding a subscription to itself, or adding `null` or `undefined` will not perform any\n * operation at all. (A noop).\n *\n * `Subscription` instances that are added to this instance will automatically remove themselves\n * if they are unsubscribed. Functions and {@link Unsubscribable} objects that you wish to remove\n * will need to be removed manually with {@link #remove}\n *\n * @param teardown The finalization logic to add to this subscription.\n */\n add(teardown: TeardownLogic): void {\n // Only add the finalizer if it's not undefined\n // and don't add a subscription to itself.\n if (teardown && teardown !== this) {\n if (this.closed) {\n // If this subscription is already closed,\n // execute whatever finalizer is handed to it automatically.\n execFinalizer(teardown);\n } else {\n if (teardown instanceof Subscription) {\n // We don't add closed subscriptions, and we don't add the same subscription\n // twice. Subscription unsubscribe is idempotent.\n if (teardown.closed || teardown._hasParent(this)) {\n return;\n }\n teardown._addParent(this);\n }\n (this._finalizers = this._finalizers ?? []).push(teardown);\n }\n }\n }\n\n /**\n * Checks to see if a this subscription already has a particular parent.\n * This will signal that this subscription has already been added to the parent in question.\n * @param parent the parent to check for\n */\n private _hasParent(parent: Subscription) {\n const { _parentage } = this;\n return _parentage === parent || (Array.isArray(_parentage) && _parentage.includes(parent));\n }\n\n /**\n * Adds a parent to this subscription so it can be removed from the parent if it\n * unsubscribes on it's own.\n *\n * NOTE: THIS ASSUMES THAT {@link _hasParent} HAS ALREADY BEEN CHECKED.\n * @param parent The parent subscription to add\n */\n private _addParent(parent: Subscription) {\n const { _parentage } = this;\n this._parentage = Array.isArray(_parentage) ? (_parentage.push(parent), _parentage) : _parentage ? [_parentage, parent] : parent;\n }\n\n /**\n * Called on a child when it is removed via {@link #remove}.\n * @param parent The parent to remove\n */\n private _removeParent(parent: Subscription) {\n const { _parentage } = this;\n if (_parentage === parent) {\n this._parentage = null;\n } else if (Array.isArray(_parentage)) {\n arrRemove(_parentage, parent);\n }\n }\n\n /**\n * Removes a finalizer from this subscription that was previously added with the {@link #add} method.\n *\n * Note that `Subscription` instances, when unsubscribed, will automatically remove themselves\n * from every other `Subscription` they have been added to. This means that using the `remove` method\n * is not a common thing and should be used thoughtfully.\n *\n * If you add the same finalizer instance of a function or an unsubscribable object to a `Subscription` instance\n * more than once, you will need to call `remove` the same number of times to remove all instances.\n *\n * All finalizer instances are removed to free up memory upon unsubscription.\n *\n * @param teardown The finalizer to remove from this subscription\n */\n remove(teardown: Exclude): void {\n const { _finalizers } = this;\n _finalizers && arrRemove(_finalizers, teardown);\n\n if (teardown instanceof Subscription) {\n teardown._removeParent(this);\n }\n }\n}\n\nexport const EMPTY_SUBSCRIPTION = Subscription.EMPTY;\n\nexport function isSubscription(value: any): value is Subscription {\n return (\n value instanceof Subscription ||\n (value && 'closed' in value && isFunction(value.remove) && isFunction(value.add) && isFunction(value.unsubscribe))\n );\n}\n\nfunction execFinalizer(finalizer: Unsubscribable | (() => void)) {\n if (isFunction(finalizer)) {\n finalizer();\n } else {\n finalizer.unsubscribe();\n }\n}\n", "import { Subscriber } from './Subscriber';\nimport { ObservableNotification } from './types';\n\n/**\n * The {@link GlobalConfig} object for RxJS. It is used to configure things\n * like how to react on unhandled errors.\n */\nexport const config: GlobalConfig = {\n onUnhandledError: null,\n onStoppedNotification: null,\n Promise: undefined,\n useDeprecatedSynchronousErrorHandling: false,\n useDeprecatedNextContext: false,\n};\n\n/**\n * The global configuration object for RxJS, used to configure things\n * like how to react on unhandled errors. Accessible via {@link config}\n * object.\n */\nexport interface GlobalConfig {\n /**\n * A registration point for unhandled errors from RxJS. These are errors that\n * cannot were not handled by consuming code in the usual subscription path. For\n * example, if you have this configured, and you subscribe to an observable without\n * providing an error handler, errors from that subscription will end up here. This\n * will _always_ be called asynchronously on another job in the runtime. This is because\n * we do not want errors thrown in this user-configured handler to interfere with the\n * behavior of the library.\n */\n onUnhandledError: ((err: any) => void) | null;\n\n /**\n * A registration point for notifications that cannot be sent to subscribers because they\n * have completed, errored or have been explicitly unsubscribed. By default, next, complete\n * and error notifications sent to stopped subscribers are noops. However, sometimes callers\n * might want a different behavior. For example, with sources that attempt to report errors\n * to stopped subscribers, a caller can configure RxJS to throw an unhandled error instead.\n * This will _always_ be called asynchronously on another job in the runtime. This is because\n * we do not want errors thrown in this user-configured handler to interfere with the\n * behavior of the library.\n */\n onStoppedNotification: ((notification: ObservableNotification, subscriber: Subscriber) => void) | null;\n\n /**\n * The promise constructor used by default for {@link Observable#toPromise toPromise} and {@link Observable#forEach forEach}\n * methods.\n *\n * @deprecated As of version 8, RxJS will no longer support this sort of injection of a\n * Promise constructor. If you need a Promise implementation other than native promises,\n * please polyfill/patch Promise as you see appropriate. Will be removed in v8.\n */\n Promise?: PromiseConstructorLike;\n\n /**\n * If true, turns on synchronous error rethrowing, which is a deprecated behavior\n * in v6 and higher. This behavior enables bad patterns like wrapping a subscribe\n * call in a try/catch block. It also enables producer interference, a nasty bug\n * where a multicast can be broken for all observers by a downstream consumer with\n * an unhandled error. DO NOT USE THIS FLAG UNLESS IT'S NEEDED TO BUY TIME\n * FOR MIGRATION REASONS.\n *\n * @deprecated As of version 8, RxJS will no longer support synchronous throwing\n * of unhandled errors. All errors will be thrown on a separate call stack to prevent bad\n * behaviors described above. Will be removed in v8.\n */\n useDeprecatedSynchronousErrorHandling: boolean;\n\n /**\n * If true, enables an as-of-yet undocumented feature from v5: The ability to access\n * `unsubscribe()` via `this` context in `next` functions created in observers passed\n * to `subscribe`.\n *\n * This is being removed because the performance was severely problematic, and it could also cause\n * issues when types other than POJOs are passed to subscribe as subscribers, as they will likely have\n * their `this` context overwritten.\n *\n * @deprecated As of version 8, RxJS will no longer support altering the\n * context of next functions provided as part of an observer to Subscribe. Instead,\n * you will have access to a subscription or a signal or token that will allow you to do things like\n * unsubscribe and test closed status. Will be removed in v8.\n */\n useDeprecatedNextContext: boolean;\n}\n", "import type { TimerHandle } from './timerHandle';\ntype SetTimeoutFunction = (handler: () => void, timeout?: number, ...args: any[]) => TimerHandle;\ntype ClearTimeoutFunction = (handle: TimerHandle) => void;\n\ninterface TimeoutProvider {\n setTimeout: SetTimeoutFunction;\n clearTimeout: ClearTimeoutFunction;\n delegate:\n | {\n setTimeout: SetTimeoutFunction;\n clearTimeout: ClearTimeoutFunction;\n }\n | undefined;\n}\n\nexport const timeoutProvider: TimeoutProvider = {\n // When accessing the delegate, use the variable rather than `this` so that\n // the functions can be called without being bound to the provider.\n setTimeout(handler: () => void, timeout?: number, ...args) {\n const { delegate } = timeoutProvider;\n if (delegate?.setTimeout) {\n return delegate.setTimeout(handler, timeout, ...args);\n }\n return setTimeout(handler, timeout, ...args);\n },\n clearTimeout(handle) {\n const { delegate } = timeoutProvider;\n return (delegate?.clearTimeout || clearTimeout)(handle as any);\n },\n delegate: undefined,\n};\n", "import { config } from '../config';\nimport { timeoutProvider } from '../scheduler/timeoutProvider';\n\n/**\n * Handles an error on another job either with the user-configured {@link onUnhandledError},\n * or by throwing it on that new job so it can be picked up by `window.onerror`, `process.on('error')`, etc.\n *\n * This should be called whenever there is an error that is out-of-band with the subscription\n * or when an error hits a terminal boundary of the subscription and no error handler was provided.\n *\n * @param err the error to report\n */\nexport function reportUnhandledError(err: any) {\n timeoutProvider.setTimeout(() => {\n const { onUnhandledError } = config;\n if (onUnhandledError) {\n // Execute the user-configured error handler.\n onUnhandledError(err);\n } else {\n // Throw so it is picked up by the runtime's uncaught error mechanism.\n throw err;\n }\n });\n}\n", "/* tslint:disable:no-empty */\nexport function noop() { }\n", "import { CompleteNotification, NextNotification, ErrorNotification } from './types';\n\n/**\n * A completion object optimized for memory use and created to be the\n * same \"shape\" as other notifications in v8.\n * @internal\n */\nexport const COMPLETE_NOTIFICATION = (() => createNotification('C', undefined, undefined) as CompleteNotification)();\n\n/**\n * Internal use only. Creates an optimized error notification that is the same \"shape\"\n * as other notifications.\n * @internal\n */\nexport function errorNotification(error: any): ErrorNotification {\n return createNotification('E', undefined, error) as any;\n}\n\n/**\n * Internal use only. Creates an optimized next notification that is the same \"shape\"\n * as other notifications.\n * @internal\n */\nexport function nextNotification(value: T) {\n return createNotification('N', value, undefined) as NextNotification;\n}\n\n/**\n * Ensures that all notifications created internally have the same \"shape\" in v8.\n *\n * TODO: This is only exported to support a crazy legacy test in `groupBy`.\n * @internal\n */\nexport function createNotification(kind: 'N' | 'E' | 'C', value: any, error: any) {\n return {\n kind,\n value,\n error,\n };\n}\n", "import { config } from '../config';\n\nlet context: { errorThrown: boolean; error: any } | null = null;\n\n/**\n * Handles dealing with errors for super-gross mode. Creates a context, in which\n * any synchronously thrown errors will be passed to {@link captureError}. Which\n * will record the error such that it will be rethrown after the call back is complete.\n * TODO: Remove in v8\n * @param cb An immediately executed function.\n */\nexport function errorContext(cb: () => void) {\n if (config.useDeprecatedSynchronousErrorHandling) {\n const isRoot = !context;\n if (isRoot) {\n context = { errorThrown: false, error: null };\n }\n cb();\n if (isRoot) {\n const { errorThrown, error } = context!;\n context = null;\n if (errorThrown) {\n throw error;\n }\n }\n } else {\n // This is the general non-deprecated path for everyone that\n // isn't crazy enough to use super-gross mode (useDeprecatedSynchronousErrorHandling)\n cb();\n }\n}\n\n/**\n * Captures errors only in super-gross mode.\n * @param err the error to capture\n */\nexport function captureError(err: any) {\n if (config.useDeprecatedSynchronousErrorHandling && context) {\n context.errorThrown = true;\n context.error = err;\n }\n}\n", "import { isFunction } from './util/isFunction';\nimport { Observer, ObservableNotification } from './types';\nimport { isSubscription, Subscription } from './Subscription';\nimport { config } from './config';\nimport { reportUnhandledError } from './util/reportUnhandledError';\nimport { noop } from './util/noop';\nimport { nextNotification, errorNotification, COMPLETE_NOTIFICATION } from './NotificationFactories';\nimport { timeoutProvider } from './scheduler/timeoutProvider';\nimport { captureError } from './util/errorContext';\n\n/**\n * Implements the {@link Observer} interface and extends the\n * {@link Subscription} class. While the {@link Observer} is the public API for\n * consuming the values of an {@link Observable}, all Observers get converted to\n * a Subscriber, in order to provide Subscription-like capabilities such as\n * `unsubscribe`. Subscriber is a common type in RxJS, and crucial for\n * implementing operators, but it is rarely used as a public API.\n *\n * @class Subscriber\n */\nexport class Subscriber extends Subscription implements Observer {\n /**\n * A static factory for a Subscriber, given a (potentially partial) definition\n * of an Observer.\n * @param next The `next` callback of an Observer.\n * @param error The `error` callback of an\n * Observer.\n * @param complete The `complete` callback of an\n * Observer.\n * @return A Subscriber wrapping the (partially defined)\n * Observer represented by the given arguments.\n * @nocollapse\n * @deprecated Do not use. Will be removed in v8. There is no replacement for this\n * method, and there is no reason to be creating instances of `Subscriber` directly.\n * If you have a specific use case, please file an issue.\n */\n static create(next?: (x?: T) => void, error?: (e?: any) => void, complete?: () => void): Subscriber {\n return new SafeSubscriber(next, error, complete);\n }\n\n /** @deprecated Internal implementation detail, do not use directly. Will be made internal in v8. */\n protected isStopped: boolean = false;\n /** @deprecated Internal implementation detail, do not use directly. Will be made internal in v8. */\n protected destination: Subscriber | Observer; // this `any` is the escape hatch to erase extra type param (e.g. R)\n\n /**\n * @deprecated Internal implementation detail, do not use directly. Will be made internal in v8.\n * There is no reason to directly create an instance of Subscriber. This type is exported for typings reasons.\n */\n constructor(destination?: Subscriber | Observer) {\n super();\n if (destination) {\n this.destination = destination;\n // Automatically chain subscriptions together here.\n // if destination is a Subscription, then it is a Subscriber.\n if (isSubscription(destination)) {\n destination.add(this);\n }\n } else {\n this.destination = EMPTY_OBSERVER;\n }\n }\n\n /**\n * The {@link Observer} callback to receive notifications of type `next` from\n * the Observable, with a value. The Observable may call this method 0 or more\n * times.\n * @param {T} [value] The `next` value.\n * @return {void}\n */\n next(value?: T): void {\n if (this.isStopped) {\n handleStoppedNotification(nextNotification(value), this);\n } else {\n this._next(value!);\n }\n }\n\n /**\n * The {@link Observer} callback to receive notifications of type `error` from\n * the Observable, with an attached `Error`. Notifies the Observer that\n * the Observable has experienced an error condition.\n * @param {any} [err] The `error` exception.\n * @return {void}\n */\n error(err?: any): void {\n if (this.isStopped) {\n handleStoppedNotification(errorNotification(err), this);\n } else {\n this.isStopped = true;\n this._error(err);\n }\n }\n\n /**\n * The {@link Observer} callback to receive a valueless notification of type\n * `complete` from the Observable. Notifies the Observer that the Observable\n * has finished sending push-based notifications.\n * @return {void}\n */\n complete(): void {\n if (this.isStopped) {\n handleStoppedNotification(COMPLETE_NOTIFICATION, this);\n } else {\n this.isStopped = true;\n this._complete();\n }\n }\n\n unsubscribe(): void {\n if (!this.closed) {\n this.isStopped = true;\n super.unsubscribe();\n this.destination = null!;\n }\n }\n\n protected _next(value: T): void {\n this.destination.next(value);\n }\n\n protected _error(err: any): void {\n try {\n this.destination.error(err);\n } finally {\n this.unsubscribe();\n }\n }\n\n protected _complete(): void {\n try {\n this.destination.complete();\n } finally {\n this.unsubscribe();\n }\n }\n}\n\n/**\n * This bind is captured here because we want to be able to have\n * compatibility with monoid libraries that tend to use a method named\n * `bind`. In particular, a library called Monio requires this.\n */\nconst _bind = Function.prototype.bind;\n\nfunction bind any>(fn: Fn, thisArg: any): Fn {\n return _bind.call(fn, thisArg);\n}\n\n/**\n * Internal optimization only, DO NOT EXPOSE.\n * @internal\n */\nclass ConsumerObserver implements Observer {\n constructor(private partialObserver: Partial>) {}\n\n next(value: T): void {\n const { partialObserver } = this;\n if (partialObserver.next) {\n try {\n partialObserver.next(value);\n } catch (error) {\n handleUnhandledError(error);\n }\n }\n }\n\n error(err: any): void {\n const { partialObserver } = this;\n if (partialObserver.error) {\n try {\n partialObserver.error(err);\n } catch (error) {\n handleUnhandledError(error);\n }\n } else {\n handleUnhandledError(err);\n }\n }\n\n complete(): void {\n const { partialObserver } = this;\n if (partialObserver.complete) {\n try {\n partialObserver.complete();\n } catch (error) {\n handleUnhandledError(error);\n }\n }\n }\n}\n\nexport class SafeSubscriber extends Subscriber {\n constructor(\n observerOrNext?: Partial> | ((value: T) => void) | null,\n error?: ((e?: any) => void) | null,\n complete?: (() => void) | null\n ) {\n super();\n\n let partialObserver: Partial>;\n if (isFunction(observerOrNext) || !observerOrNext) {\n // The first argument is a function, not an observer. The next\n // two arguments *could* be observers, or they could be empty.\n partialObserver = {\n next: (observerOrNext ?? undefined) as (((value: T) => void) | undefined),\n error: error ?? undefined,\n complete: complete ?? undefined,\n };\n } else {\n // The first argument is a partial observer.\n let context: any;\n if (this && config.useDeprecatedNextContext) {\n // This is a deprecated path that made `this.unsubscribe()` available in\n // next handler functions passed to subscribe. This only exists behind a flag\n // now, as it is *very* slow.\n context = Object.create(observerOrNext);\n context.unsubscribe = () => this.unsubscribe();\n partialObserver = {\n next: observerOrNext.next && bind(observerOrNext.next, context),\n error: observerOrNext.error && bind(observerOrNext.error, context),\n complete: observerOrNext.complete && bind(observerOrNext.complete, context),\n };\n } else {\n // The \"normal\" path. Just use the partial observer directly.\n partialObserver = observerOrNext;\n }\n }\n\n // Wrap the partial observer to ensure it's a full observer, and\n // make sure proper error handling is accounted for.\n this.destination = new ConsumerObserver(partialObserver);\n }\n}\n\nfunction handleUnhandledError(error: any) {\n if (config.useDeprecatedSynchronousErrorHandling) {\n captureError(error);\n } else {\n // Ideal path, we report this as an unhandled error,\n // which is thrown on a new call stack.\n reportUnhandledError(error);\n }\n}\n\n/**\n * An error handler used when no error handler was supplied\n * to the SafeSubscriber -- meaning no error handler was supplied\n * do the `subscribe` call on our observable.\n * @param err The error to handle\n */\nfunction defaultErrorHandler(err: any) {\n throw err;\n}\n\n/**\n * A handler for notifications that cannot be sent to a stopped subscriber.\n * @param notification The notification being sent\n * @param subscriber The stopped subscriber\n */\nfunction handleStoppedNotification(notification: ObservableNotification, subscriber: Subscriber) {\n const { onStoppedNotification } = config;\n onStoppedNotification && timeoutProvider.setTimeout(() => onStoppedNotification(notification, subscriber));\n}\n\n/**\n * The observer used as a stub for subscriptions where the user did not\n * pass any arguments to `subscribe`. Comes with the default error handling\n * behavior.\n */\nexport const EMPTY_OBSERVER: Readonly> & { closed: true } = {\n closed: true,\n next: noop,\n error: defaultErrorHandler,\n complete: noop,\n};\n", "/**\n * Symbol.observable or a string \"@@observable\". Used for interop\n *\n * @deprecated We will no longer be exporting this symbol in upcoming versions of RxJS.\n * Instead polyfill and use Symbol.observable directly *or* use https://www.npmjs.com/package/symbol-observable\n */\nexport const observable: string | symbol = (() => (typeof Symbol === 'function' && Symbol.observable) || '@@observable')();\n", "/**\n * This function takes one parameter and just returns it. Simply put,\n * this is like `(x: T): T => x`.\n *\n * ## Examples\n *\n * This is useful in some cases when using things like `mergeMap`\n *\n * ```ts\n * import { interval, take, map, range, mergeMap, identity } from 'rxjs';\n *\n * const source$ = interval(1000).pipe(take(5));\n *\n * const result$ = source$.pipe(\n * map(i => range(i)),\n * mergeMap(identity) // same as mergeMap(x => x)\n * );\n *\n * result$.subscribe({\n * next: console.log\n * });\n * ```\n *\n * Or when you want to selectively apply an operator\n *\n * ```ts\n * import { interval, take, identity } from 'rxjs';\n *\n * const shouldLimit = () => Math.random() < 0.5;\n *\n * const source$ = interval(1000);\n *\n * const result$ = source$.pipe(shouldLimit() ? take(5) : identity);\n *\n * result$.subscribe({\n * next: console.log\n * });\n * ```\n *\n * @param x Any value that is returned by this function\n * @returns The value passed as the first parameter to this function\n */\nexport function identity(x: T): T {\n return x;\n}\n", "import { identity } from './identity';\nimport { UnaryFunction } from '../types';\n\nexport function pipe(): typeof identity;\nexport function pipe(fn1: UnaryFunction): UnaryFunction;\nexport function pipe(fn1: UnaryFunction, fn2: UnaryFunction): UnaryFunction;\nexport function pipe(fn1: UnaryFunction, fn2: UnaryFunction, fn3: UnaryFunction): UnaryFunction;\nexport function pipe(\n fn1: UnaryFunction,\n fn2: UnaryFunction,\n fn3: UnaryFunction,\n fn4: UnaryFunction\n): UnaryFunction;\nexport function pipe(\n fn1: UnaryFunction,\n fn2: UnaryFunction,\n fn3: UnaryFunction,\n fn4: UnaryFunction,\n fn5: UnaryFunction\n): UnaryFunction;\nexport function pipe(\n fn1: UnaryFunction,\n fn2: UnaryFunction,\n fn3: UnaryFunction,\n fn4: UnaryFunction,\n fn5: UnaryFunction,\n fn6: UnaryFunction\n): UnaryFunction;\nexport function pipe(\n fn1: UnaryFunction,\n fn2: UnaryFunction,\n fn3: UnaryFunction,\n fn4: UnaryFunction,\n fn5: UnaryFunction,\n fn6: UnaryFunction,\n fn7: UnaryFunction\n): UnaryFunction;\nexport function pipe(\n fn1: UnaryFunction,\n fn2: UnaryFunction,\n fn3: UnaryFunction,\n fn4: UnaryFunction,\n fn5: UnaryFunction,\n fn6: UnaryFunction,\n fn7: UnaryFunction,\n fn8: UnaryFunction\n): UnaryFunction;\nexport function pipe(\n fn1: UnaryFunction,\n fn2: UnaryFunction,\n fn3: UnaryFunction,\n fn4: UnaryFunction,\n fn5: UnaryFunction,\n fn6: UnaryFunction,\n fn7: UnaryFunction,\n fn8: UnaryFunction,\n fn9: UnaryFunction\n): UnaryFunction;\nexport function pipe(\n fn1: UnaryFunction,\n fn2: UnaryFunction,\n fn3: UnaryFunction,\n fn4: UnaryFunction,\n fn5: UnaryFunction,\n fn6: UnaryFunction,\n fn7: UnaryFunction,\n fn8: UnaryFunction,\n fn9: UnaryFunction,\n ...fns: UnaryFunction[]\n): UnaryFunction;\n\n/**\n * pipe() can be called on one or more functions, each of which can take one argument (\"UnaryFunction\")\n * and uses it to return a value.\n * It returns a function that takes one argument, passes it to the first UnaryFunction, and then\n * passes the result to the next one, passes that result to the next one, and so on. \n */\nexport function pipe(...fns: Array>): UnaryFunction {\n return pipeFromArray(fns);\n}\n\n/** @internal */\nexport function pipeFromArray(fns: Array>): UnaryFunction {\n if (fns.length === 0) {\n return identity as UnaryFunction;\n }\n\n if (fns.length === 1) {\n return fns[0];\n }\n\n return function piped(input: T): R {\n return fns.reduce((prev: any, fn: UnaryFunction) => fn(prev), input as any);\n };\n}\n", "import { Operator } from './Operator';\nimport { SafeSubscriber, Subscriber } from './Subscriber';\nimport { isSubscription, Subscription } from './Subscription';\nimport { TeardownLogic, OperatorFunction, Subscribable, Observer } from './types';\nimport { observable as Symbol_observable } from './symbol/observable';\nimport { pipeFromArray } from './util/pipe';\nimport { config } from './config';\nimport { isFunction } from './util/isFunction';\nimport { errorContext } from './util/errorContext';\n\n/**\n * A representation of any set of values over any amount of time. This is the most basic building block\n * of RxJS.\n *\n * @class Observable\n */\nexport class Observable implements Subscribable {\n /**\n * @deprecated Internal implementation detail, do not use directly. Will be made internal in v8.\n */\n source: Observable | undefined;\n\n /**\n * @deprecated Internal implementation detail, do not use directly. Will be made internal in v8.\n */\n operator: Operator | undefined;\n\n /**\n * @constructor\n * @param {Function} subscribe the function that is called when the Observable is\n * initially subscribed to. This function is given a Subscriber, to which new values\n * can be `next`ed, or an `error` method can be called to raise an error, or\n * `complete` can be called to notify of a successful completion.\n */\n constructor(subscribe?: (this: Observable, subscriber: Subscriber) => TeardownLogic) {\n if (subscribe) {\n this._subscribe = subscribe;\n }\n }\n\n // HACK: Since TypeScript inherits static properties too, we have to\n // fight against TypeScript here so Subject can have a different static create signature\n /**\n * Creates a new Observable by calling the Observable constructor\n * @owner Observable\n * @method create\n * @param {Function} subscribe? the subscriber function to be passed to the Observable constructor\n * @return {Observable} a new observable\n * @nocollapse\n * @deprecated Use `new Observable()` instead. Will be removed in v8.\n */\n static create: (...args: any[]) => any = (subscribe?: (subscriber: Subscriber) => TeardownLogic) => {\n return new Observable(subscribe);\n };\n\n /**\n * Creates a new Observable, with this Observable instance as the source, and the passed\n * operator defined as the new observable's operator.\n * @method lift\n * @param operator the operator defining the operation to take on the observable\n * @return a new observable with the Operator applied\n * @deprecated Internal implementation detail, do not use directly. Will be made internal in v8.\n * If you have implemented an operator using `lift`, it is recommended that you create an\n * operator by simply returning `new Observable()` directly. See \"Creating new operators from\n * scratch\" section here: https://rxjs.dev/guide/operators\n */\n lift(operator?: Operator): Observable {\n const observable = new Observable();\n observable.source = this;\n observable.operator = operator;\n return observable;\n }\n\n subscribe(observerOrNext?: Partial> | ((value: T) => void)): Subscription;\n /** @deprecated Instead of passing separate callback arguments, use an observer argument. Signatures taking separate callback arguments will be removed in v8. Details: https://rxjs.dev/deprecations/subscribe-arguments */\n subscribe(next?: ((value: T) => void) | null, error?: ((error: any) => void) | null, complete?: (() => void) | null): Subscription;\n /**\n * Invokes an execution of an Observable and registers Observer handlers for notifications it will emit.\n *\n * Use it when you have all these Observables, but still nothing is happening.\n *\n * `subscribe` is not a regular operator, but a method that calls Observable's internal `subscribe` function. It\n * might be for example a function that you passed to Observable's constructor, but most of the time it is\n * a library implementation, which defines what will be emitted by an Observable, and when it be will emitted. This means\n * that calling `subscribe` is actually the moment when Observable starts its work, not when it is created, as it is often\n * the thought.\n *\n * Apart from starting the execution of an Observable, this method allows you to listen for values\n * that an Observable emits, as well as for when it completes or errors. You can achieve this in two\n * of the following ways.\n *\n * The first way is creating an object that implements {@link Observer} interface. It should have methods\n * defined by that interface, but note that it should be just a regular JavaScript object, which you can create\n * yourself in any way you want (ES6 class, classic function constructor, object literal etc.). In particular, do\n * not attempt to use any RxJS implementation details to create Observers - you don't need them. Remember also\n * that your object does not have to implement all methods. If you find yourself creating a method that doesn't\n * do anything, you can simply omit it. Note however, if the `error` method is not provided and an error happens,\n * it will be thrown asynchronously. Errors thrown asynchronously cannot be caught using `try`/`catch`. Instead,\n * use the {@link onUnhandledError} configuration option or use a runtime handler (like `window.onerror` or\n * `process.on('error)`) to be notified of unhandled errors. Because of this, it's recommended that you provide\n * an `error` method to avoid missing thrown errors.\n *\n * The second way is to give up on Observer object altogether and simply provide callback functions in place of its methods.\n * This means you can provide three functions as arguments to `subscribe`, where the first function is equivalent\n * of a `next` method, the second of an `error` method and the third of a `complete` method. Just as in case of an Observer,\n * if you do not need to listen for something, you can omit a function by passing `undefined` or `null`,\n * since `subscribe` recognizes these functions by where they were placed in function call. When it comes\n * to the `error` function, as with an Observer, if not provided, errors emitted by an Observable will be thrown asynchronously.\n *\n * You can, however, subscribe with no parameters at all. This may be the case where you're not interested in terminal events\n * and you also handled emissions internally by using operators (e.g. using `tap`).\n *\n * Whichever style of calling `subscribe` you use, in both cases it returns a Subscription object.\n * This object allows you to call `unsubscribe` on it, which in turn will stop the work that an Observable does and will clean\n * up all resources that an Observable used. Note that cancelling a subscription will not call `complete` callback\n * provided to `subscribe` function, which is reserved for a regular completion signal that comes from an Observable.\n *\n * Remember that callbacks provided to `subscribe` are not guaranteed to be called asynchronously.\n * It is an Observable itself that decides when these functions will be called. For example {@link of}\n * by default emits all its values synchronously. Always check documentation for how given Observable\n * will behave when subscribed and if its default behavior can be modified with a `scheduler`.\n *\n * #### Examples\n *\n * Subscribe with an {@link guide/observer Observer}\n *\n * ```ts\n * import { of } from 'rxjs';\n *\n * const sumObserver = {\n * sum: 0,\n * next(value) {\n * console.log('Adding: ' + value);\n * this.sum = this.sum + value;\n * },\n * error() {\n * // We actually could just remove this method,\n * // since we do not really care about errors right now.\n * },\n * complete() {\n * console.log('Sum equals: ' + this.sum);\n * }\n * };\n *\n * of(1, 2, 3) // Synchronously emits 1, 2, 3 and then completes.\n * .subscribe(sumObserver);\n *\n * // Logs:\n * // 'Adding: 1'\n * // 'Adding: 2'\n * // 'Adding: 3'\n * // 'Sum equals: 6'\n * ```\n *\n * Subscribe with functions ({@link deprecations/subscribe-arguments deprecated})\n *\n * ```ts\n * import { of } from 'rxjs'\n *\n * let sum = 0;\n *\n * of(1, 2, 3).subscribe(\n * value => {\n * console.log('Adding: ' + value);\n * sum = sum + value;\n * },\n * undefined,\n * () => console.log('Sum equals: ' + sum)\n * );\n *\n * // Logs:\n * // 'Adding: 1'\n * // 'Adding: 2'\n * // 'Adding: 3'\n * // 'Sum equals: 6'\n * ```\n *\n * Cancel a subscription\n *\n * ```ts\n * import { interval } from 'rxjs';\n *\n * const subscription = interval(1000).subscribe({\n * next(num) {\n * console.log(num)\n * },\n * complete() {\n * // Will not be called, even when cancelling subscription.\n * console.log('completed!');\n * }\n * });\n *\n * setTimeout(() => {\n * subscription.unsubscribe();\n * console.log('unsubscribed!');\n * }, 2500);\n *\n * // Logs:\n * // 0 after 1s\n * // 1 after 2s\n * // 'unsubscribed!' after 2.5s\n * ```\n *\n * @param {Observer|Function} observerOrNext (optional) Either an observer with methods to be called,\n * or the first of three possible handlers, which is the handler for each value emitted from the subscribed\n * Observable.\n * @param {Function} error (optional) A handler for a terminal event resulting from an error. If no error handler is provided,\n * the error will be thrown asynchronously as unhandled.\n * @param {Function} complete (optional) A handler for a terminal event resulting from successful completion.\n * @return {Subscription} a subscription reference to the registered handlers\n * @method subscribe\n */\n subscribe(\n observerOrNext?: Partial> | ((value: T) => void) | null,\n error?: ((error: any) => void) | null,\n complete?: (() => void) | null\n ): Subscription {\n const subscriber = isSubscriber(observerOrNext) ? observerOrNext : new SafeSubscriber(observerOrNext, error, complete);\n\n errorContext(() => {\n const { operator, source } = this;\n subscriber.add(\n operator\n ? // We're dealing with a subscription in the\n // operator chain to one of our lifted operators.\n operator.call(subscriber, source)\n : source\n ? // If `source` has a value, but `operator` does not, something that\n // had intimate knowledge of our API, like our `Subject`, must have\n // set it. We're going to just call `_subscribe` directly.\n this._subscribe(subscriber)\n : // In all other cases, we're likely wrapping a user-provided initializer\n // function, so we need to catch errors and handle them appropriately.\n this._trySubscribe(subscriber)\n );\n });\n\n return subscriber;\n }\n\n /** @internal */\n protected _trySubscribe(sink: Subscriber): TeardownLogic {\n try {\n return this._subscribe(sink);\n } catch (err) {\n // We don't need to return anything in this case,\n // because it's just going to try to `add()` to a subscription\n // above.\n sink.error(err);\n }\n }\n\n /**\n * Used as a NON-CANCELLABLE means of subscribing to an observable, for use with\n * APIs that expect promises, like `async/await`. You cannot unsubscribe from this.\n *\n * **WARNING**: Only use this with observables you *know* will complete. If the source\n * observable does not complete, you will end up with a promise that is hung up, and\n * potentially all of the state of an async function hanging out in memory. To avoid\n * this situation, look into adding something like {@link timeout}, {@link take},\n * {@link takeWhile}, or {@link takeUntil} amongst others.\n *\n * #### Example\n *\n * ```ts\n * import { interval, take } from 'rxjs';\n *\n * const source$ = interval(1000).pipe(take(4));\n *\n * async function getTotal() {\n * let total = 0;\n *\n * await source$.forEach(value => {\n * total += value;\n * console.log('observable -> ' + value);\n * });\n *\n * return total;\n * }\n *\n * getTotal().then(\n * total => console.log('Total: ' + total)\n * );\n *\n * // Expected:\n * // 'observable -> 0'\n * // 'observable -> 1'\n * // 'observable -> 2'\n * // 'observable -> 3'\n * // 'Total: 6'\n * ```\n *\n * @param next a handler for each value emitted by the observable\n * @return a promise that either resolves on observable completion or\n * rejects with the handled error\n */\n forEach(next: (value: T) => void): Promise;\n\n /**\n * @param next a handler for each value emitted by the observable\n * @param promiseCtor a constructor function used to instantiate the Promise\n * @return a promise that either resolves on observable completion or\n * rejects with the handled error\n * @deprecated Passing a Promise constructor will no longer be available\n * in upcoming versions of RxJS. This is because it adds weight to the library, for very\n * little benefit. If you need this functionality, it is recommended that you either\n * polyfill Promise, or you create an adapter to convert the returned native promise\n * to whatever promise implementation you wanted. Will be removed in v8.\n */\n forEach(next: (value: T) => void, promiseCtor: PromiseConstructorLike): Promise;\n\n forEach(next: (value: T) => void, promiseCtor?: PromiseConstructorLike): Promise {\n promiseCtor = getPromiseCtor(promiseCtor);\n\n return new promiseCtor((resolve, reject) => {\n const subscriber = new SafeSubscriber({\n next: (value) => {\n try {\n next(value);\n } catch (err) {\n reject(err);\n subscriber.unsubscribe();\n }\n },\n error: reject,\n complete: resolve,\n });\n this.subscribe(subscriber);\n }) as Promise;\n }\n\n /** @internal */\n protected _subscribe(subscriber: Subscriber): TeardownLogic {\n return this.source?.subscribe(subscriber);\n }\n\n /**\n * An interop point defined by the es7-observable spec https://github.com/zenparsing/es-observable\n * @method Symbol.observable\n * @return {Observable} this instance of the observable\n */\n [Symbol_observable]() {\n return this;\n }\n\n /* tslint:disable:max-line-length */\n pipe(): Observable;\n pipe(op1: OperatorFunction): Observable;\n pipe(op1: OperatorFunction, op2: OperatorFunction): Observable;\n pipe(op1: OperatorFunction, op2: OperatorFunction, op3: OperatorFunction): Observable;\n pipe(\n op1: OperatorFunction,\n op2: OperatorFunction,\n op3: OperatorFunction,\n op4: OperatorFunction\n ): Observable;\n pipe(\n op1: OperatorFunction,\n op2: OperatorFunction,\n op3: OperatorFunction,\n op4: OperatorFunction,\n op5: OperatorFunction\n ): Observable;\n pipe(\n op1: OperatorFunction,\n op2: OperatorFunction,\n op3: OperatorFunction,\n op4: OperatorFunction,\n op5: OperatorFunction,\n op6: OperatorFunction\n ): Observable;\n pipe(\n op1: OperatorFunction,\n op2: OperatorFunction,\n op3: OperatorFunction,\n op4: OperatorFunction,\n op5: OperatorFunction,\n op6: OperatorFunction,\n op7: OperatorFunction\n ): Observable;\n pipe(\n op1: OperatorFunction,\n op2: OperatorFunction,\n op3: OperatorFunction,\n op4: OperatorFunction,\n op5: OperatorFunction,\n op6: OperatorFunction,\n op7: OperatorFunction,\n op8: OperatorFunction\n ): Observable;\n pipe(\n op1: OperatorFunction,\n op2: OperatorFunction,\n op3: OperatorFunction,\n op4: OperatorFunction,\n op5: OperatorFunction,\n op6: OperatorFunction,\n op7: OperatorFunction,\n op8: OperatorFunction,\n op9: OperatorFunction\n ): Observable;\n pipe(\n op1: OperatorFunction,\n op2: OperatorFunction,\n op3: OperatorFunction,\n op4: OperatorFunction,\n op5: OperatorFunction,\n op6: OperatorFunction,\n op7: OperatorFunction,\n op8: OperatorFunction,\n op9: OperatorFunction,\n ...operations: OperatorFunction[]\n ): Observable;\n /* tslint:enable:max-line-length */\n\n /**\n * Used to stitch together functional operators into a chain.\n * @method pipe\n * @return {Observable} the Observable result of all of the operators having\n * been called in the order they were passed in.\n *\n * ## Example\n *\n * ```ts\n * import { interval, filter, map, scan } from 'rxjs';\n *\n * interval(1000)\n * .pipe(\n * filter(x => x % 2 === 0),\n * map(x => x + x),\n * scan((acc, x) => acc + x)\n * )\n * .subscribe(x => console.log(x));\n * ```\n */\n pipe(...operations: OperatorFunction[]): Observable {\n return pipeFromArray(operations)(this);\n }\n\n /* tslint:disable:max-line-length */\n /** @deprecated Replaced with {@link firstValueFrom} and {@link lastValueFrom}. Will be removed in v8. Details: https://rxjs.dev/deprecations/to-promise */\n toPromise(): Promise;\n /** @deprecated Replaced with {@link firstValueFrom} and {@link lastValueFrom}. Will be removed in v8. Details: https://rxjs.dev/deprecations/to-promise */\n toPromise(PromiseCtor: typeof Promise): Promise;\n /** @deprecated Replaced with {@link firstValueFrom} and {@link lastValueFrom}. Will be removed in v8. Details: https://rxjs.dev/deprecations/to-promise */\n toPromise(PromiseCtor: PromiseConstructorLike): Promise;\n /* tslint:enable:max-line-length */\n\n /**\n * Subscribe to this Observable and get a Promise resolving on\n * `complete` with the last emission (if any).\n *\n * **WARNING**: Only use this with observables you *know* will complete. If the source\n * observable does not complete, you will end up with a promise that is hung up, and\n * potentially all of the state of an async function hanging out in memory. To avoid\n * this situation, look into adding something like {@link timeout}, {@link take},\n * {@link takeWhile}, or {@link takeUntil} amongst others.\n *\n * @method toPromise\n * @param [promiseCtor] a constructor function used to instantiate\n * the Promise\n * @return A Promise that resolves with the last value emit, or\n * rejects on an error. If there were no emissions, Promise\n * resolves with undefined.\n * @deprecated Replaced with {@link firstValueFrom} and {@link lastValueFrom}. Will be removed in v8. Details: https://rxjs.dev/deprecations/to-promise\n */\n toPromise(promiseCtor?: PromiseConstructorLike): Promise {\n promiseCtor = getPromiseCtor(promiseCtor);\n\n return new promiseCtor((resolve, reject) => {\n let value: T | undefined;\n this.subscribe(\n (x: T) => (value = x),\n (err: any) => reject(err),\n () => resolve(value)\n );\n }) as Promise;\n }\n}\n\n/**\n * Decides between a passed promise constructor from consuming code,\n * A default configured promise constructor, and the native promise\n * constructor and returns it. If nothing can be found, it will throw\n * an error.\n * @param promiseCtor The optional promise constructor to passed by consuming code\n */\nfunction getPromiseCtor(promiseCtor: PromiseConstructorLike | undefined) {\n return promiseCtor ?? config.Promise ?? Promise;\n}\n\nfunction isObserver(value: any): value is Observer {\n return value && isFunction(value.next) && isFunction(value.error) && isFunction(value.complete);\n}\n\nfunction isSubscriber(value: any): value is Subscriber {\n return (value && value instanceof Subscriber) || (isObserver(value) && isSubscription(value));\n}\n", "import { Observable } from '../Observable';\nimport { Subscriber } from '../Subscriber';\nimport { OperatorFunction } from '../types';\nimport { isFunction } from './isFunction';\n\n/**\n * Used to determine if an object is an Observable with a lift function.\n */\nexport function hasLift(source: any): source is { lift: InstanceType['lift'] } {\n return isFunction(source?.lift);\n}\n\n/**\n * Creates an `OperatorFunction`. Used to define operators throughout the library in a concise way.\n * @param init The logic to connect the liftedSource to the subscriber at the moment of subscription.\n */\nexport function operate(\n init: (liftedSource: Observable, subscriber: Subscriber) => (() => void) | void\n): OperatorFunction {\n return (source: Observable) => {\n if (hasLift(source)) {\n return source.lift(function (this: Subscriber, liftedSource: Observable) {\n try {\n return init(liftedSource, this);\n } catch (err) {\n this.error(err);\n }\n });\n }\n throw new TypeError('Unable to lift unknown Observable type');\n };\n}\n", "import { Subscriber } from '../Subscriber';\n\n/**\n * Creates an instance of an `OperatorSubscriber`.\n * @param destination The downstream subscriber.\n * @param onNext Handles next values, only called if this subscriber is not stopped or closed. Any\n * error that occurs in this function is caught and sent to the `error` method of this subscriber.\n * @param onError Handles errors from the subscription, any errors that occur in this handler are caught\n * and send to the `destination` error handler.\n * @param onComplete Handles completion notification from the subscription. Any errors that occur in\n * this handler are sent to the `destination` error handler.\n * @param onFinalize Additional teardown logic here. This will only be called on teardown if the\n * subscriber itself is not already closed. This is called after all other teardown logic is executed.\n */\nexport function createOperatorSubscriber(\n destination: Subscriber,\n onNext?: (value: T) => void,\n onComplete?: () => void,\n onError?: (err: any) => void,\n onFinalize?: () => void\n): Subscriber {\n return new OperatorSubscriber(destination, onNext, onComplete, onError, onFinalize);\n}\n\n/**\n * A generic helper for allowing operators to be created with a Subscriber and\n * use closures to capture necessary state from the operator function itself.\n */\nexport class OperatorSubscriber extends Subscriber {\n /**\n * Creates an instance of an `OperatorSubscriber`.\n * @param destination The downstream subscriber.\n * @param onNext Handles next values, only called if this subscriber is not stopped or closed. Any\n * error that occurs in this function is caught and sent to the `error` method of this subscriber.\n * @param onError Handles errors from the subscription, any errors that occur in this handler are caught\n * and send to the `destination` error handler.\n * @param onComplete Handles completion notification from the subscription. Any errors that occur in\n * this handler are sent to the `destination` error handler.\n * @param onFinalize Additional finalization logic here. This will only be called on finalization if the\n * subscriber itself is not already closed. This is called after all other finalization logic is executed.\n * @param shouldUnsubscribe An optional check to see if an unsubscribe call should truly unsubscribe.\n * NOTE: This currently **ONLY** exists to support the strange behavior of {@link groupBy}, where unsubscription\n * to the resulting observable does not actually disconnect from the source if there are active subscriptions\n * to any grouped observable. (DO NOT EXPOSE OR USE EXTERNALLY!!!)\n */\n constructor(\n destination: Subscriber,\n onNext?: (value: T) => void,\n onComplete?: () => void,\n onError?: (err: any) => void,\n private onFinalize?: () => void,\n private shouldUnsubscribe?: () => boolean\n ) {\n // It's important - for performance reasons - that all of this class's\n // members are initialized and that they are always initialized in the same\n // order. This will ensure that all OperatorSubscriber instances have the\n // same hidden class in V8. This, in turn, will help keep the number of\n // hidden classes involved in property accesses within the base class as\n // low as possible. If the number of hidden classes involved exceeds four,\n // the property accesses will become megamorphic and performance penalties\n // will be incurred - i.e. inline caches won't be used.\n //\n // The reasons for ensuring all instances have the same hidden class are\n // further discussed in this blog post from Benedikt Meurer:\n // https://benediktmeurer.de/2018/03/23/impact-of-polymorphism-on-component-based-frameworks-like-react/\n super(destination);\n this._next = onNext\n ? function (this: OperatorSubscriber, value: T) {\n try {\n onNext(value);\n } catch (err) {\n destination.error(err);\n }\n }\n : super._next;\n this._error = onError\n ? function (this: OperatorSubscriber, err: any) {\n try {\n onError(err);\n } catch (err) {\n // Send any errors that occur down stream.\n destination.error(err);\n } finally {\n // Ensure finalization.\n this.unsubscribe();\n }\n }\n : super._error;\n this._complete = onComplete\n ? function (this: OperatorSubscriber) {\n try {\n onComplete();\n } catch (err) {\n // Send any errors that occur down stream.\n destination.error(err);\n } finally {\n // Ensure finalization.\n this.unsubscribe();\n }\n }\n : super._complete;\n }\n\n unsubscribe() {\n if (!this.shouldUnsubscribe || this.shouldUnsubscribe()) {\n const { closed } = this;\n super.unsubscribe();\n // Execute additional teardown if we have any and we didn't already do so.\n !closed && this.onFinalize?.();\n }\n }\n}\n", "import { Subscription } from '../Subscription';\n\ninterface AnimationFrameProvider {\n schedule(callback: FrameRequestCallback): Subscription;\n requestAnimationFrame: typeof requestAnimationFrame;\n cancelAnimationFrame: typeof cancelAnimationFrame;\n delegate:\n | {\n requestAnimationFrame: typeof requestAnimationFrame;\n cancelAnimationFrame: typeof cancelAnimationFrame;\n }\n | undefined;\n}\n\nexport const animationFrameProvider: AnimationFrameProvider = {\n // When accessing the delegate, use the variable rather than `this` so that\n // the functions can be called without being bound to the provider.\n schedule(callback) {\n let request = requestAnimationFrame;\n let cancel: typeof cancelAnimationFrame | undefined = cancelAnimationFrame;\n const { delegate } = animationFrameProvider;\n if (delegate) {\n request = delegate.requestAnimationFrame;\n cancel = delegate.cancelAnimationFrame;\n }\n const handle = request((timestamp) => {\n // Clear the cancel function. The request has been fulfilled, so\n // attempting to cancel the request upon unsubscription would be\n // pointless.\n cancel = undefined;\n callback(timestamp);\n });\n return new Subscription(() => cancel?.(handle));\n },\n requestAnimationFrame(...args) {\n const { delegate } = animationFrameProvider;\n return (delegate?.requestAnimationFrame || requestAnimationFrame)(...args);\n },\n cancelAnimationFrame(...args) {\n const { delegate } = animationFrameProvider;\n return (delegate?.cancelAnimationFrame || cancelAnimationFrame)(...args);\n },\n delegate: undefined,\n};\n", "import { createErrorClass } from './createErrorClass';\n\nexport interface ObjectUnsubscribedError extends Error {}\n\nexport interface ObjectUnsubscribedErrorCtor {\n /**\n * @deprecated Internal implementation detail. Do not construct error instances.\n * Cannot be tagged as internal: https://github.com/ReactiveX/rxjs/issues/6269\n */\n new (): ObjectUnsubscribedError;\n}\n\n/**\n * An error thrown when an action is invalid because the object has been\n * unsubscribed.\n *\n * @see {@link Subject}\n * @see {@link BehaviorSubject}\n *\n * @class ObjectUnsubscribedError\n */\nexport const ObjectUnsubscribedError: ObjectUnsubscribedErrorCtor = createErrorClass(\n (_super) =>\n function ObjectUnsubscribedErrorImpl(this: any) {\n _super(this);\n this.name = 'ObjectUnsubscribedError';\n this.message = 'object unsubscribed';\n }\n);\n", "import { Operator } from './Operator';\nimport { Observable } from './Observable';\nimport { Subscriber } from './Subscriber';\nimport { Subscription, EMPTY_SUBSCRIPTION } from './Subscription';\nimport { Observer, SubscriptionLike, TeardownLogic } from './types';\nimport { ObjectUnsubscribedError } from './util/ObjectUnsubscribedError';\nimport { arrRemove } from './util/arrRemove';\nimport { errorContext } from './util/errorContext';\n\n/**\n * A Subject is a special type of Observable that allows values to be\n * multicasted to many Observers. Subjects are like EventEmitters.\n *\n * Every Subject is an Observable and an Observer. You can subscribe to a\n * Subject, and you can call next to feed values as well as error and complete.\n */\nexport class Subject extends Observable implements SubscriptionLike {\n closed = false;\n\n private currentObservers: Observer[] | null = null;\n\n /** @deprecated Internal implementation detail, do not use directly. Will be made internal in v8. */\n observers: Observer[] = [];\n /** @deprecated Internal implementation detail, do not use directly. Will be made internal in v8. */\n isStopped = false;\n /** @deprecated Internal implementation detail, do not use directly. Will be made internal in v8. */\n hasError = false;\n /** @deprecated Internal implementation detail, do not use directly. Will be made internal in v8. */\n thrownError: any = null;\n\n /**\n * Creates a \"subject\" by basically gluing an observer to an observable.\n *\n * @nocollapse\n * @deprecated Recommended you do not use. Will be removed at some point in the future. Plans for replacement still under discussion.\n */\n static create: (...args: any[]) => any = (destination: Observer, source: Observable): AnonymousSubject => {\n return new AnonymousSubject(destination, source);\n };\n\n constructor() {\n // NOTE: This must be here to obscure Observable's constructor.\n super();\n }\n\n /** @deprecated Internal implementation detail, do not use directly. Will be made internal in v8. */\n lift(operator: Operator): Observable {\n const subject = new AnonymousSubject(this, this);\n subject.operator = operator as any;\n return subject as any;\n }\n\n /** @internal */\n protected _throwIfClosed() {\n if (this.closed) {\n throw new ObjectUnsubscribedError();\n }\n }\n\n next(value: T) {\n errorContext(() => {\n this._throwIfClosed();\n if (!this.isStopped) {\n if (!this.currentObservers) {\n this.currentObservers = Array.from(this.observers);\n }\n for (const observer of this.currentObservers) {\n observer.next(value);\n }\n }\n });\n }\n\n error(err: any) {\n errorContext(() => {\n this._throwIfClosed();\n if (!this.isStopped) {\n this.hasError = this.isStopped = true;\n this.thrownError = err;\n const { observers } = this;\n while (observers.length) {\n observers.shift()!.error(err);\n }\n }\n });\n }\n\n complete() {\n errorContext(() => {\n this._throwIfClosed();\n if (!this.isStopped) {\n this.isStopped = true;\n const { observers } = this;\n while (observers.length) {\n observers.shift()!.complete();\n }\n }\n });\n }\n\n unsubscribe() {\n this.isStopped = this.closed = true;\n this.observers = this.currentObservers = null!;\n }\n\n get observed() {\n return this.observers?.length > 0;\n }\n\n /** @internal */\n protected _trySubscribe(subscriber: Subscriber): TeardownLogic {\n this._throwIfClosed();\n return super._trySubscribe(subscriber);\n }\n\n /** @internal */\n protected _subscribe(subscriber: Subscriber): Subscription {\n this._throwIfClosed();\n this._checkFinalizedStatuses(subscriber);\n return this._innerSubscribe(subscriber);\n }\n\n /** @internal */\n protected _innerSubscribe(subscriber: Subscriber) {\n const { hasError, isStopped, observers } = this;\n if (hasError || isStopped) {\n return EMPTY_SUBSCRIPTION;\n }\n this.currentObservers = null;\n observers.push(subscriber);\n return new Subscription(() => {\n this.currentObservers = null;\n arrRemove(observers, subscriber);\n });\n }\n\n /** @internal */\n protected _checkFinalizedStatuses(subscriber: Subscriber) {\n const { hasError, thrownError, isStopped } = this;\n if (hasError) {\n subscriber.error(thrownError);\n } else if (isStopped) {\n subscriber.complete();\n }\n }\n\n /**\n * Creates a new Observable with this Subject as the source. You can do this\n * to create custom Observer-side logic of the Subject and conceal it from\n * code that uses the Observable.\n * @return {Observable} Observable that the Subject casts to\n */\n asObservable(): Observable {\n const observable: any = new Observable();\n observable.source = this;\n return observable;\n }\n}\n\n/**\n * @class AnonymousSubject\n */\nexport class AnonymousSubject extends Subject {\n constructor(\n /** @deprecated Internal implementation detail, do not use directly. Will be made internal in v8. */\n public destination?: Observer,\n source?: Observable\n ) {\n super();\n this.source = source;\n }\n\n next(value: T) {\n this.destination?.next?.(value);\n }\n\n error(err: any) {\n this.destination?.error?.(err);\n }\n\n complete() {\n this.destination?.complete?.();\n }\n\n /** @internal */\n protected _subscribe(subscriber: Subscriber): Subscription {\n return this.source?.subscribe(subscriber) ?? EMPTY_SUBSCRIPTION;\n }\n}\n", "import { TimestampProvider } from '../types';\n\ninterface DateTimestampProvider extends TimestampProvider {\n delegate: TimestampProvider | undefined;\n}\n\nexport const dateTimestampProvider: DateTimestampProvider = {\n now() {\n // Use the variable rather than `this` so that the function can be called\n // without being bound to the provider.\n return (dateTimestampProvider.delegate || Date).now();\n },\n delegate: undefined,\n};\n", "import { Subject } from './Subject';\nimport { TimestampProvider } from './types';\nimport { Subscriber } from './Subscriber';\nimport { Subscription } from './Subscription';\nimport { dateTimestampProvider } from './scheduler/dateTimestampProvider';\n\n/**\n * A variant of {@link Subject} that \"replays\" old values to new subscribers by emitting them when they first subscribe.\n *\n * `ReplaySubject` has an internal buffer that will store a specified number of values that it has observed. Like `Subject`,\n * `ReplaySubject` \"observes\" values by having them passed to its `next` method. When it observes a value, it will store that\n * value for a time determined by the configuration of the `ReplaySubject`, as passed to its constructor.\n *\n * When a new subscriber subscribes to the `ReplaySubject` instance, it will synchronously emit all values in its buffer in\n * a First-In-First-Out (FIFO) manner. The `ReplaySubject` will also complete, if it has observed completion; and it will\n * error if it has observed an error.\n *\n * There are two main configuration items to be concerned with:\n *\n * 1. `bufferSize` - This will determine how many items are stored in the buffer, defaults to infinite.\n * 2. `windowTime` - The amount of time to hold a value in the buffer before removing it from the buffer.\n *\n * Both configurations may exist simultaneously. So if you would like to buffer a maximum of 3 values, as long as the values\n * are less than 2 seconds old, you could do so with a `new ReplaySubject(3, 2000)`.\n *\n * ### Differences with BehaviorSubject\n *\n * `BehaviorSubject` is similar to `new ReplaySubject(1)`, with a couple of exceptions:\n *\n * 1. `BehaviorSubject` comes \"primed\" with a single value upon construction.\n * 2. `ReplaySubject` will replay values, even after observing an error, where `BehaviorSubject` will not.\n *\n * @see {@link Subject}\n * @see {@link BehaviorSubject}\n * @see {@link shareReplay}\n */\nexport class ReplaySubject extends Subject {\n private _buffer: (T | number)[] = [];\n private _infiniteTimeWindow = true;\n\n /**\n * @param bufferSize The size of the buffer to replay on subscription\n * @param windowTime The amount of time the buffered items will stay buffered\n * @param timestampProvider An object with a `now()` method that provides the current timestamp. This is used to\n * calculate the amount of time something has been buffered.\n */\n constructor(\n private _bufferSize = Infinity,\n private _windowTime = Infinity,\n private _timestampProvider: TimestampProvider = dateTimestampProvider\n ) {\n super();\n this._infiniteTimeWindow = _windowTime === Infinity;\n this._bufferSize = Math.max(1, _bufferSize);\n this._windowTime = Math.max(1, _windowTime);\n }\n\n next(value: T): void {\n const { isStopped, _buffer, _infiniteTimeWindow, _timestampProvider, _windowTime } = this;\n if (!isStopped) {\n _buffer.push(value);\n !_infiniteTimeWindow && _buffer.push(_timestampProvider.now() + _windowTime);\n }\n this._trimBuffer();\n super.next(value);\n }\n\n /** @internal */\n protected _subscribe(subscriber: Subscriber): Subscription {\n this._throwIfClosed();\n this._trimBuffer();\n\n const subscription = this._innerSubscribe(subscriber);\n\n const { _infiniteTimeWindow, _buffer } = this;\n // We use a copy here, so reentrant code does not mutate our array while we're\n // emitting it to a new subscriber.\n const copy = _buffer.slice();\n for (let i = 0; i < copy.length && !subscriber.closed; i += _infiniteTimeWindow ? 1 : 2) {\n subscriber.next(copy[i] as T);\n }\n\n this._checkFinalizedStatuses(subscriber);\n\n return subscription;\n }\n\n private _trimBuffer() {\n const { _bufferSize, _timestampProvider, _buffer, _infiniteTimeWindow } = this;\n // If we don't have an infinite buffer size, and we're over the length,\n // use splice to truncate the old buffer values off. Note that we have to\n // double the size for instances where we're not using an infinite time window\n // because we're storing the values and the timestamps in the same array.\n const adjustedBufferSize = (_infiniteTimeWindow ? 1 : 2) * _bufferSize;\n _bufferSize < Infinity && adjustedBufferSize < _buffer.length && _buffer.splice(0, _buffer.length - adjustedBufferSize);\n\n // Now, if we're not in an infinite time window, remove all values where the time is\n // older than what is allowed.\n if (!_infiniteTimeWindow) {\n const now = _timestampProvider.now();\n let last = 0;\n // Search the array for the first timestamp that isn't expired and\n // truncate the buffer up to that point.\n for (let i = 1; i < _buffer.length && (_buffer[i] as number) <= now; i += 2) {\n last = i;\n }\n last && _buffer.splice(0, last + 1);\n }\n }\n}\n", "import { Scheduler } from '../Scheduler';\nimport { Subscription } from '../Subscription';\nimport { SchedulerAction } from '../types';\n\n/**\n * A unit of work to be executed in a `scheduler`. An action is typically\n * created from within a {@link SchedulerLike} and an RxJS user does not need to concern\n * themselves about creating and manipulating an Action.\n *\n * ```ts\n * class Action extends Subscription {\n * new (scheduler: Scheduler, work: (state?: T) => void);\n * schedule(state?: T, delay: number = 0): Subscription;\n * }\n * ```\n *\n * @class Action\n */\nexport class Action extends Subscription {\n constructor(scheduler: Scheduler, work: (this: SchedulerAction, state?: T) => void) {\n super();\n }\n /**\n * Schedules this action on its parent {@link SchedulerLike} for execution. May be passed\n * some context object, `state`. May happen at some point in the future,\n * according to the `delay` parameter, if specified.\n * @param {T} [state] Some contextual data that the `work` function uses when\n * called by the Scheduler.\n * @param {number} [delay] Time to wait before executing the work, where the\n * time unit is implicit and defined by the Scheduler.\n * @return {void}\n */\n public schedule(state?: T, delay: number = 0): Subscription {\n return this;\n }\n}\n", "import type { TimerHandle } from './timerHandle';\ntype SetIntervalFunction = (handler: () => void, timeout?: number, ...args: any[]) => TimerHandle;\ntype ClearIntervalFunction = (handle: TimerHandle) => void;\n\ninterface IntervalProvider {\n setInterval: SetIntervalFunction;\n clearInterval: ClearIntervalFunction;\n delegate:\n | {\n setInterval: SetIntervalFunction;\n clearInterval: ClearIntervalFunction;\n }\n | undefined;\n}\n\nexport const intervalProvider: IntervalProvider = {\n // When accessing the delegate, use the variable rather than `this` so that\n // the functions can be called without being bound to the provider.\n setInterval(handler: () => void, timeout?: number, ...args) {\n const { delegate } = intervalProvider;\n if (delegate?.setInterval) {\n return delegate.setInterval(handler, timeout, ...args);\n }\n return setInterval(handler, timeout, ...args);\n },\n clearInterval(handle) {\n const { delegate } = intervalProvider;\n return (delegate?.clearInterval || clearInterval)(handle as any);\n },\n delegate: undefined,\n};\n", "import { Action } from './Action';\nimport { SchedulerAction } from '../types';\nimport { Subscription } from '../Subscription';\nimport { AsyncScheduler } from './AsyncScheduler';\nimport { intervalProvider } from './intervalProvider';\nimport { arrRemove } from '../util/arrRemove';\nimport { TimerHandle } from './timerHandle';\n\nexport class AsyncAction extends Action {\n public id: TimerHandle | undefined;\n public state?: T;\n // @ts-ignore: Property has no initializer and is not definitely assigned\n public delay: number;\n protected pending: boolean = false;\n\n constructor(protected scheduler: AsyncScheduler, protected work: (this: SchedulerAction, state?: T) => void) {\n super(scheduler, work);\n }\n\n public schedule(state?: T, delay: number = 0): Subscription {\n if (this.closed) {\n return this;\n }\n\n // Always replace the current state with the new state.\n this.state = state;\n\n const id = this.id;\n const scheduler = this.scheduler;\n\n //\n // Important implementation note:\n //\n // Actions only execute once by default, unless rescheduled from within the\n // scheduled callback. This allows us to implement single and repeat\n // actions via the same code path, without adding API surface area, as well\n // as mimic traditional recursion but across asynchronous boundaries.\n //\n // However, JS runtimes and timers distinguish between intervals achieved by\n // serial `setTimeout` calls vs. a single `setInterval` call. An interval of\n // serial `setTimeout` calls can be individually delayed, which delays\n // scheduling the next `setTimeout`, and so on. `setInterval` attempts to\n // guarantee the interval callback will be invoked more precisely to the\n // interval period, regardless of load.\n //\n // Therefore, we use `setInterval` to schedule single and repeat actions.\n // If the action reschedules itself with the same delay, the interval is not\n // canceled. If the action doesn't reschedule, or reschedules with a\n // different delay, the interval will be canceled after scheduled callback\n // execution.\n //\n if (id != null) {\n this.id = this.recycleAsyncId(scheduler, id, delay);\n }\n\n // Set the pending flag indicating that this action has been scheduled, or\n // has recursively rescheduled itself.\n this.pending = true;\n\n this.delay = delay;\n // If this action has already an async Id, don't request a new one.\n this.id = this.id ?? this.requestAsyncId(scheduler, this.id, delay);\n\n return this;\n }\n\n protected requestAsyncId(scheduler: AsyncScheduler, _id?: TimerHandle, delay: number = 0): TimerHandle {\n return intervalProvider.setInterval(scheduler.flush.bind(scheduler, this), delay);\n }\n\n protected recycleAsyncId(_scheduler: AsyncScheduler, id?: TimerHandle, delay: number | null = 0): TimerHandle | undefined {\n // If this action is rescheduled with the same delay time, don't clear the interval id.\n if (delay != null && this.delay === delay && this.pending === false) {\n return id;\n }\n // Otherwise, if the action's delay time is different from the current delay,\n // or the action has been rescheduled before it's executed, clear the interval id\n if (id != null) {\n intervalProvider.clearInterval(id);\n }\n\n return undefined;\n }\n\n /**\n * Immediately executes this action and the `work` it contains.\n * @return {any}\n */\n public execute(state: T, delay: number): any {\n if (this.closed) {\n return new Error('executing a cancelled action');\n }\n\n this.pending = false;\n const error = this._execute(state, delay);\n if (error) {\n return error;\n } else if (this.pending === false && this.id != null) {\n // Dequeue if the action didn't reschedule itself. Don't call\n // unsubscribe(), because the action could reschedule later.\n // For example:\n // ```\n // scheduler.schedule(function doWork(counter) {\n // /* ... I'm a busy worker bee ... */\n // var originalAction = this;\n // /* wait 100ms before rescheduling the action */\n // setTimeout(function () {\n // originalAction.schedule(counter + 1);\n // }, 100);\n // }, 1000);\n // ```\n this.id = this.recycleAsyncId(this.scheduler, this.id, null);\n }\n }\n\n protected _execute(state: T, _delay: number): any {\n let errored: boolean = false;\n let errorValue: any;\n try {\n this.work(state);\n } catch (e) {\n errored = true;\n // HACK: Since code elsewhere is relying on the \"truthiness\" of the\n // return here, we can't have it return \"\" or 0 or false.\n // TODO: Clean this up when we refactor schedulers mid-version-8 or so.\n errorValue = e ? e : new Error('Scheduled action threw falsy error');\n }\n if (errored) {\n this.unsubscribe();\n return errorValue;\n }\n }\n\n unsubscribe() {\n if (!this.closed) {\n const { id, scheduler } = this;\n const { actions } = scheduler;\n\n this.work = this.state = this.scheduler = null!;\n this.pending = false;\n\n arrRemove(actions, this);\n if (id != null) {\n this.id = this.recycleAsyncId(scheduler, id, null);\n }\n\n this.delay = null!;\n super.unsubscribe();\n }\n }\n}\n", "import { Action } from './scheduler/Action';\nimport { Subscription } from './Subscription';\nimport { SchedulerLike, SchedulerAction } from './types';\nimport { dateTimestampProvider } from './scheduler/dateTimestampProvider';\n\n/**\n * An execution context and a data structure to order tasks and schedule their\n * execution. Provides a notion of (potentially virtual) time, through the\n * `now()` getter method.\n *\n * Each unit of work in a Scheduler is called an `Action`.\n *\n * ```ts\n * class Scheduler {\n * now(): number;\n * schedule(work, delay?, state?): Subscription;\n * }\n * ```\n *\n * @class Scheduler\n * @deprecated Scheduler is an internal implementation detail of RxJS, and\n * should not be used directly. Rather, create your own class and implement\n * {@link SchedulerLike}. Will be made internal in v8.\n */\nexport class Scheduler implements SchedulerLike {\n public static now: () => number = dateTimestampProvider.now;\n\n constructor(private schedulerActionCtor: typeof Action, now: () => number = Scheduler.now) {\n this.now = now;\n }\n\n /**\n * A getter method that returns a number representing the current time\n * (at the time this function was called) according to the scheduler's own\n * internal clock.\n * @return {number} A number that represents the current time. May or may not\n * have a relation to wall-clock time. May or may not refer to a time unit\n * (e.g. milliseconds).\n */\n public now: () => number;\n\n /**\n * Schedules a function, `work`, for execution. May happen at some point in\n * the future, according to the `delay` parameter, if specified. May be passed\n * some context object, `state`, which will be passed to the `work` function.\n *\n * The given arguments will be processed an stored as an Action object in a\n * queue of actions.\n *\n * @param {function(state: ?T): ?Subscription} work A function representing a\n * task, or some unit of work to be executed by the Scheduler.\n * @param {number} [delay] Time to wait before executing the work, where the\n * time unit is implicit and defined by the Scheduler itself.\n * @param {T} [state] Some contextual data that the `work` function uses when\n * called by the Scheduler.\n * @return {Subscription} A subscription in order to be able to unsubscribe\n * the scheduled work.\n */\n public schedule(work: (this: SchedulerAction, state?: T) => void, delay: number = 0, state?: T): Subscription {\n return new this.schedulerActionCtor(this, work).schedule(state, delay);\n }\n}\n", "import { Scheduler } from '../Scheduler';\nimport { Action } from './Action';\nimport { AsyncAction } from './AsyncAction';\nimport { TimerHandle } from './timerHandle';\n\nexport class AsyncScheduler extends Scheduler {\n public actions: Array> = [];\n /**\n * A flag to indicate whether the Scheduler is currently executing a batch of\n * queued actions.\n * @type {boolean}\n * @internal\n */\n public _active: boolean = false;\n /**\n * An internal ID used to track the latest asynchronous task such as those\n * coming from `setTimeout`, `setInterval`, `requestAnimationFrame`, and\n * others.\n * @type {any}\n * @internal\n */\n public _scheduled: TimerHandle | undefined;\n\n constructor(SchedulerAction: typeof Action, now: () => number = Scheduler.now) {\n super(SchedulerAction, now);\n }\n\n public flush(action: AsyncAction): void {\n const { actions } = this;\n\n if (this._active) {\n actions.push(action);\n return;\n }\n\n let error: any;\n this._active = true;\n\n do {\n if ((error = action.execute(action.state, action.delay))) {\n break;\n }\n } while ((action = actions.shift()!)); // exhaust the scheduler queue\n\n this._active = false;\n\n if (error) {\n while ((action = actions.shift()!)) {\n action.unsubscribe();\n }\n throw error;\n }\n }\n}\n", "import { AsyncAction } from './AsyncAction';\nimport { AsyncScheduler } from './AsyncScheduler';\n\n/**\n *\n * Async Scheduler\n *\n * Schedule task as if you used setTimeout(task, duration)\n *\n * `async` scheduler schedules tasks asynchronously, by putting them on the JavaScript\n * event loop queue. It is best used to delay tasks in time or to schedule tasks repeating\n * in intervals.\n *\n * If you just want to \"defer\" task, that is to perform it right after currently\n * executing synchronous code ends (commonly achieved by `setTimeout(deferredTask, 0)`),\n * better choice will be the {@link asapScheduler} scheduler.\n *\n * ## Examples\n * Use async scheduler to delay task\n * ```ts\n * import { asyncScheduler } from 'rxjs';\n *\n * const task = () => console.log('it works!');\n *\n * asyncScheduler.schedule(task, 2000);\n *\n * // After 2 seconds logs:\n * // \"it works!\"\n * ```\n *\n * Use async scheduler to repeat task in intervals\n * ```ts\n * import { asyncScheduler } from 'rxjs';\n *\n * function task(state) {\n * console.log(state);\n * this.schedule(state + 1, 1000); // `this` references currently executing Action,\n * // which we reschedule with new state and delay\n * }\n *\n * asyncScheduler.schedule(task, 3000, 0);\n *\n * // Logs:\n * // 0 after 3s\n * // 1 after 4s\n * // 2 after 5s\n * // 3 after 6s\n * ```\n */\n\nexport const asyncScheduler = new AsyncScheduler(AsyncAction);\n\n/**\n * @deprecated Renamed to {@link asyncScheduler}. Will be removed in v8.\n */\nexport const async = asyncScheduler;\n", "import { AsyncAction } from './AsyncAction';\nimport { AnimationFrameScheduler } from './AnimationFrameScheduler';\nimport { SchedulerAction } from '../types';\nimport { animationFrameProvider } from './animationFrameProvider';\nimport { TimerHandle } from './timerHandle';\n\nexport class AnimationFrameAction extends AsyncAction {\n constructor(protected scheduler: AnimationFrameScheduler, protected work: (this: SchedulerAction, state?: T) => void) {\n super(scheduler, work);\n }\n\n protected requestAsyncId(scheduler: AnimationFrameScheduler, id?: TimerHandle, delay: number = 0): TimerHandle {\n // If delay is greater than 0, request as an async action.\n if (delay !== null && delay > 0) {\n return super.requestAsyncId(scheduler, id, delay);\n }\n // Push the action to the end of the scheduler queue.\n scheduler.actions.push(this);\n // If an animation frame has already been requested, don't request another\n // one. If an animation frame hasn't been requested yet, request one. Return\n // the current animation frame request id.\n return scheduler._scheduled || (scheduler._scheduled = animationFrameProvider.requestAnimationFrame(() => scheduler.flush(undefined)));\n }\n\n protected recycleAsyncId(scheduler: AnimationFrameScheduler, id?: TimerHandle, delay: number = 0): TimerHandle | undefined {\n // If delay exists and is greater than 0, or if the delay is null (the\n // action wasn't rescheduled) but was originally scheduled as an async\n // action, then recycle as an async action.\n if (delay != null ? delay > 0 : this.delay > 0) {\n return super.recycleAsyncId(scheduler, id, delay);\n }\n // If the scheduler queue has no remaining actions with the same async id,\n // cancel the requested animation frame and set the scheduled flag to\n // undefined so the next AnimationFrameAction will request its own.\n const { actions } = scheduler;\n if (id != null && actions[actions.length - 1]?.id !== id) {\n animationFrameProvider.cancelAnimationFrame(id as number);\n scheduler._scheduled = undefined;\n }\n // Return undefined so the action knows to request a new async id if it's rescheduled.\n return undefined;\n }\n}\n", "import { AsyncAction } from './AsyncAction';\nimport { AsyncScheduler } from './AsyncScheduler';\n\nexport class AnimationFrameScheduler extends AsyncScheduler {\n public flush(action?: AsyncAction): void {\n this._active = true;\n // The async id that effects a call to flush is stored in _scheduled.\n // Before executing an action, it's necessary to check the action's async\n // id to determine whether it's supposed to be executed in the current\n // flush.\n // Previous implementations of this method used a count to determine this,\n // but that was unsound, as actions that are unsubscribed - i.e. cancelled -\n // are removed from the actions array and that can shift actions that are\n // scheduled to be executed in a subsequent flush into positions at which\n // they are executed within the current flush.\n const flushId = this._scheduled;\n this._scheduled = undefined;\n\n const { actions } = this;\n let error: any;\n action = action || actions.shift()!;\n\n do {\n if ((error = action.execute(action.state, action.delay))) {\n break;\n }\n } while ((action = actions[0]) && action.id === flushId && actions.shift());\n\n this._active = false;\n\n if (error) {\n while ((action = actions[0]) && action.id === flushId && actions.shift()) {\n action.unsubscribe();\n }\n throw error;\n }\n }\n}\n", "import { AnimationFrameAction } from './AnimationFrameAction';\nimport { AnimationFrameScheduler } from './AnimationFrameScheduler';\n\n/**\n *\n * Animation Frame Scheduler\n *\n * Perform task when `window.requestAnimationFrame` would fire\n *\n * When `animationFrame` scheduler is used with delay, it will fall back to {@link asyncScheduler} scheduler\n * behaviour.\n *\n * Without delay, `animationFrame` scheduler can be used to create smooth browser animations.\n * It makes sure scheduled task will happen just before next browser content repaint,\n * thus performing animations as efficiently as possible.\n *\n * ## Example\n * Schedule div height animation\n * ```ts\n * // html:
\n * import { animationFrameScheduler } from 'rxjs';\n *\n * const div = document.querySelector('div');\n *\n * animationFrameScheduler.schedule(function(height) {\n * div.style.height = height + \"px\";\n *\n * this.schedule(height + 1); // `this` references currently executing Action,\n * // which we reschedule with new state\n * }, 0, 0);\n *\n * // You will see a div element growing in height\n * ```\n */\n\nexport const animationFrameScheduler = new AnimationFrameScheduler(AnimationFrameAction);\n\n/**\n * @deprecated Renamed to {@link animationFrameScheduler}. Will be removed in v8.\n */\nexport const animationFrame = animationFrameScheduler;\n", "import { Observable } from '../Observable';\nimport { SchedulerLike } from '../types';\n\n/**\n * A simple Observable that emits no items to the Observer and immediately\n * emits a complete notification.\n *\n * Just emits 'complete', and nothing else.\n *\n * ![](empty.png)\n *\n * A simple Observable that only emits the complete notification. It can be used\n * for composing with other Observables, such as in a {@link mergeMap}.\n *\n * ## Examples\n *\n * Log complete notification\n *\n * ```ts\n * import { EMPTY } from 'rxjs';\n *\n * EMPTY.subscribe({\n * next: () => console.log('Next'),\n * complete: () => console.log('Complete!')\n * });\n *\n * // Outputs\n * // Complete!\n * ```\n *\n * Emit the number 7, then complete\n *\n * ```ts\n * import { EMPTY, startWith } from 'rxjs';\n *\n * const result = EMPTY.pipe(startWith(7));\n * result.subscribe(x => console.log(x));\n *\n * // Outputs\n * // 7\n * ```\n *\n * Map and flatten only odd numbers to the sequence `'a'`, `'b'`, `'c'`\n *\n * ```ts\n * import { interval, mergeMap, of, EMPTY } from 'rxjs';\n *\n * const interval$ = interval(1000);\n * const result = interval$.pipe(\n * mergeMap(x => x % 2 === 1 ? of('a', 'b', 'c') : EMPTY),\n * );\n * result.subscribe(x => console.log(x));\n *\n * // Results in the following to the console:\n * // x is equal to the count on the interval, e.g. (0, 1, 2, 3, ...)\n * // x will occur every 1000ms\n * // if x % 2 is equal to 1, print a, b, c (each on its own)\n * // if x % 2 is not equal to 1, nothing will be output\n * ```\n *\n * @see {@link Observable}\n * @see {@link NEVER}\n * @see {@link of}\n * @see {@link throwError}\n */\nexport const EMPTY = new Observable((subscriber) => subscriber.complete());\n\n/**\n * @param scheduler A {@link SchedulerLike} to use for scheduling\n * the emission of the complete notification.\n * @deprecated Replaced with the {@link EMPTY} constant or {@link scheduled} (e.g. `scheduled([], scheduler)`). Will be removed in v8.\n */\nexport function empty(scheduler?: SchedulerLike) {\n return scheduler ? emptyScheduled(scheduler) : EMPTY;\n}\n\nfunction emptyScheduled(scheduler: SchedulerLike) {\n return new Observable((subscriber) => scheduler.schedule(() => subscriber.complete()));\n}\n", "import { SchedulerLike } from '../types';\nimport { isFunction } from './isFunction';\n\nexport function isScheduler(value: any): value is SchedulerLike {\n return value && isFunction(value.schedule);\n}\n", "import { SchedulerLike } from '../types';\nimport { isFunction } from './isFunction';\nimport { isScheduler } from './isScheduler';\n\nfunction last(arr: T[]): T | undefined {\n return arr[arr.length - 1];\n}\n\nexport function popResultSelector(args: any[]): ((...args: unknown[]) => unknown) | undefined {\n return isFunction(last(args)) ? args.pop() : undefined;\n}\n\nexport function popScheduler(args: any[]): SchedulerLike | undefined {\n return isScheduler(last(args)) ? args.pop() : undefined;\n}\n\nexport function popNumber(args: any[], defaultValue: number): number {\n return typeof last(args) === 'number' ? args.pop()! : defaultValue;\n}\n", "export const isArrayLike = ((x: any): x is ArrayLike => x && typeof x.length === 'number' && typeof x !== 'function');", "import { isFunction } from \"./isFunction\";\n\n/**\n * Tests to see if the object is \"thennable\".\n * @param value the object to test\n */\nexport function isPromise(value: any): value is PromiseLike {\n return isFunction(value?.then);\n}\n", "import { InteropObservable } from '../types';\nimport { observable as Symbol_observable } from '../symbol/observable';\nimport { isFunction } from './isFunction';\n\n/** Identifies an input as being Observable (but not necessary an Rx Observable) */\nexport function isInteropObservable(input: any): input is InteropObservable {\n return isFunction(input[Symbol_observable]);\n}\n", "import { isFunction } from './isFunction';\n\nexport function isAsyncIterable(obj: any): obj is AsyncIterable {\n return Symbol.asyncIterator && isFunction(obj?.[Symbol.asyncIterator]);\n}\n", "/**\n * Creates the TypeError to throw if an invalid object is passed to `from` or `scheduled`.\n * @param input The object that was passed.\n */\nexport function createInvalidObservableTypeError(input: any) {\n // TODO: We should create error codes that can be looked up, so this can be less verbose.\n return new TypeError(\n `You provided ${\n input !== null && typeof input === 'object' ? 'an invalid object' : `'${input}'`\n } where a stream was expected. You can provide an Observable, Promise, ReadableStream, Array, AsyncIterable, or Iterable.`\n );\n}\n", "export function getSymbolIterator(): symbol {\n if (typeof Symbol !== 'function' || !Symbol.iterator) {\n return '@@iterator' as any;\n }\n\n return Symbol.iterator;\n}\n\nexport const iterator = getSymbolIterator();\n", "import { iterator as Symbol_iterator } from '../symbol/iterator';\nimport { isFunction } from './isFunction';\n\n/** Identifies an input as being an Iterable */\nexport function isIterable(input: any): input is Iterable {\n return isFunction(input?.[Symbol_iterator]);\n}\n", "import { ReadableStreamLike } from '../types';\nimport { isFunction } from './isFunction';\n\nexport async function* readableStreamLikeToAsyncGenerator(readableStream: ReadableStreamLike): AsyncGenerator {\n const reader = readableStream.getReader();\n try {\n while (true) {\n const { value, done } = await reader.read();\n if (done) {\n return;\n }\n yield value!;\n }\n } finally {\n reader.releaseLock();\n }\n}\n\nexport function isReadableStreamLike(obj: any): obj is ReadableStreamLike {\n // We don't want to use instanceof checks because they would return\n // false for instances from another Realm, like an