1008.Construct_Binary_Tree_from_Preorder_Traversal.md

leetcode 1008

https://leetcode-cn.com/problems/construct-binary-search-tree-from-preorder-traversal/

1008. Construct Binary Search Tree from Preorder Traversal

中等

Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.

It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.

A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.

A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.

Example 1:


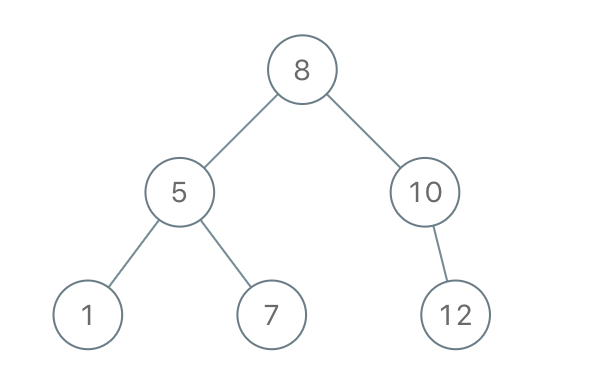
Input: preorder = [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]

Example 2:

Input: preorder = [1,3]
Output: [1,null,3]

Constraints:

• 1 <= preorder.length <= 100
• 1 <= preorder[i] <= 108
• All the values of preorder are unique.

相关企业

• 亚马逊 Amazon|2

相关标签

• Stack
• Tree
• Binary Search Tree
• Array
• Binary Tree
• Monotonic Stack

Idea

每一个subtree用preorder的第一个来切分后面的部分成左右subsubtree

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode bstFromPreorder(int[] preorder) {
        if (preorder == null || preorder.length == 0){
            return null;
        }
        return bstFromPreorder(preorder, 0, preorder.length - 1);
    }

    private TreeNode bstFromPreorder(int[] preorder, int start, int end){
        if (start > end){
            return null;
        }

        TreeNode currRoot = new TreeNode(preorder[start]);
        if (start == end){
            return currRoot;
        }
        //find left subtree
        int leftLen = 0;//this is the len of left subtree
        while(preorder[start + 1 + leftLen] < preorder[start]){
            leftLen ++;
            // System.out.println(start + " " + leftLen);
            if (start + 1 + leftLen >= preorder.length){//corner case input [4,2]
                break;
            }
        }
        currRoot.left = bstFromPreorder(preorder, start + 1, start + 1 + leftLen - 1);
        currRoot.right = bstFromPreorder(preorder, start + 1 + leftLen, end);

        return currRoot;
    }
}

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def bstFromPreorder(self, preorder: List[int]) -> TreeNode:
        if not preorder:
            return None

        currRoot = TreeNode(preorder[0])
        if len(preorder) == 1:
            return currRoot
        # find left subtree len
        leftLen = 0
        while preorder[1 + leftLen] < preorder[0]:
            leftLen += 1
            if leftLen >= len(preorder) - 1:
                break
    
        currRoot.left = self.bstFromPreorder(preorder[1 : leftLen + 1])

        # if leftLen + 1 >= len(preorder):
        #     return currRoot
        currRoot.right = self.bstFromPreorder(preorder[leftLen + 1 : ])
        return currRoot

class Solution:
    def bstFromPreorder(self, preorder: List[int]) -> TreeNode:
        if len(preorder) == 0: return None
        node = TreeNode(preorder[0])
        node.left, node.right = self.bstFromPreorder([i for i in preorder[1:] if i < preorder[0]]), 
                                self.bstFromPreorder([i for i in preorder[1:] if i > preorder[0]])
        return node

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def bstFromPreorder(self, preorder: List[int]) -> Optional[TreeNode]:
        if not preorder:
            return TreeNode()
        return self._buildtree(preorder, 0, len(preorder)-1)

    def _buildtree(self, preorder, startindex, endindex):
        if startindex > endindex:
            return 

        splitvalue = preorder[startindex]
        currNode = TreeNode(splitvalue)
        if startindex == endindex:
            return currNode

        leftLeng = 0
        while startindex+1+leftLeng <= endindex and preorder[startindex+1+leftLeng] < splitvalue:
            leftLeng += 1

        currNode.left = self._buildtree(preorder, startindex+1, startindex+1+leftLeng-1)
        currNode.right = self._buildtree(preorder, startindex+1+leftLeng, endindex)
        return currNode

Idea2

这题很特别的是他说了是binary search tree

由于树是「二叉搜索树」，我们知道「二叉搜索树」的中序遍历的结果是有序序列。我们可以对「前序遍历」的结果 排序 得到「中序遍历」的结果。于是问题就转换成为 105. 从前序与中序遍历序列构造二叉树