LeetCode_Day39,40_DP_BuyandSellStock.md

LeetCode Day 39,40 Dynamic Programming Buy and Sell Stock

121. Best Time to Buy and Sell Stock
122. Best Time to Buy and Sell Stock II
123. Best Time to Buy and Sell Stock III
188. Best Time to Buy and Sell Stock IV
309. Best Time to Buy and Sell Stock with Cooldown

121. Best Time to Buy and Sell Stock

Approach 1: Greedy

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        low = float("inf")
        result = 0
        for i in range(len(prices)):
            low = min(low, prices[i]) #取最左最小价格
            result = max(result, prices[i] - low) #直接取最大区间利润
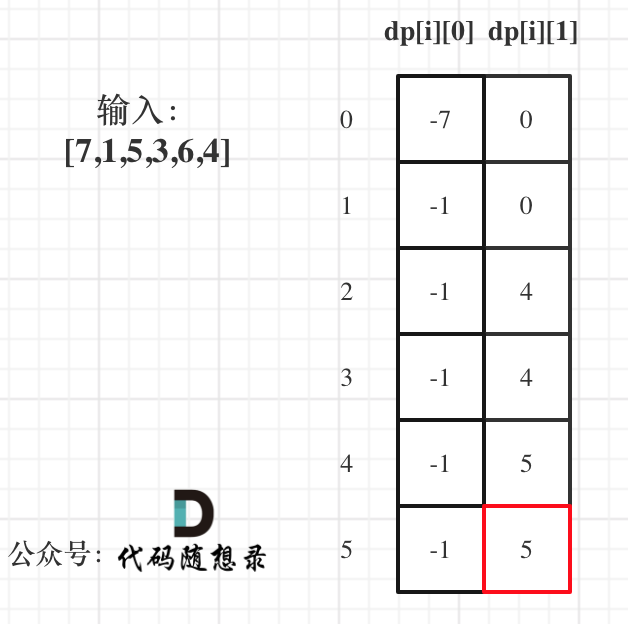
        return result

Approach 2: DP

DP List Define:

dp[i][0]: max $ if hold a stock on day i

dp[i][0]: max $ if hold no stock on day i

Recusive Relation:

dp[i][0] = max(dp[i-1][0],-prices[i] )

• dp[i-1][0]: hold a stack on i-1, remain the same on day i

• -prices[i]: buy a stack on day i

dp[i][1] = max(dp[i-1][1], prices[i] + dp[i-1][0])

• dp[i-1][1]: hold no stack on day i-1, remain the same

• prices[i] + dp[i-1][0]: throw the stack today (day i).

Initialization:

dp[0][0]: Because we hold a stock on day 0, therefore we must buy on day 0, so it will be -prices[0]

dp[0][1]: No stack on day 0, therefore 0.

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        dp = [[0,0] for _ in range(len(prices))]
        dp[0][0] = -prices[0]

        for i in range(1, len(prices)):
            dp[i][0] = max(dp[i-1][0], -prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i][0]+prices[i])
        return dp[len(prices) - 1][1]

Sum:

Using DP axtually do exactlly the same with greedy. we can see dp[i][0] maintain the min to buy, and dp[i][1] maintain the max_profit.

122. Best Time to Buy and Sell Stock II

Approach 1: Greedy

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        result = 0

        for i in range(1, len(prices)):
            profit = prices[i] - prices[i-1]
            if profit > 0 :
                result += profit

        return result

Approach 2: DP

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        dp = [[0,0] for _ in range(len(prices))]
        dp[0][0] = -prices[0]

        for i in range(1, len(prices)):
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i])
        return dp[len(prices) - 1][1]

123. Best Time to Buy and Sell Stock III

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        if len(prices) == 0:
            return 0
        dp = [0] * 5 
        dp[1] = -prices[0]
        dp[3] = -prices[0]
        for i in range(1, len(prices)):
            dp[1] = max(dp[1], dp[0] - prices[i])
            dp[2] = max(dp[2], dp[1] + prices[i])
            dp[3] = max(dp[3], dp[2] - prices[i])
            dp[4] = max(dp[4], dp[3] + prices[i])
        return dp[4]

188. Best Time to Buy and Sell Stock IV

New: k times limitation of buying/selling stock.

Challenge: Initialization when i is 0. When j is even, we can see it as it bought and sold in the same day, therefore we have the status of not holding a stock the kth time.

class Solution:
    def maxProfit(self, k: int, prices: List[int]) -> int:
        dp = [[0]*2*k for _ in range(len(prices))]

        for j in range(0, 2*k, 2):
            dp[0][j] = -prices[0]

        for i in range(1, len(prices)):
            for j in range(0, 2*k, 2): # j is even, stand for holding a stock
                if j==0:
                    dp[i][j] = max(dp[i-1][j], -prices[i])
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] - prices[i])
                dp[i][j+1] = max(dp[i-1][j+1], dp[i-1][j] + prices[i])
        
        return dp[len(prices)-1][2*k-1]

309. Best Time to Buy and Sell Stock with Cooldown

Several different status:

• Hold a stock

• Do not hold a stock

  • All other day
  • Sold a stock today
  • Cooldown day today (sold a stock yesterday)

To achieve these four status:

1. Hold a stock:

   • hold a stock yesterday (keep the same status with yesterday)
   • buy a stock today
     • Yesterday is Cooldown day
     • Yester is normal hold no stock day

   Therefore, dp[i][0] = max(dp[i-1][0], dp[i-1][3] - prices[i], dp[i-1][1] - prices[i])

2. All other day hold no stock: Hold no stock yesterday, cooldown day yesterday.

   Therefore, dp[i][1] = max(dp[i-1][1], dp[i-1][3])

3. Sold a stock today: Hold a stock yesterday.

   dp[i][2] = dp[i-1][0] + prices[i]

4. Cooldown day today: Sold a stock yesterday.

   dp[i][3] = dp[i-1][2]

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        dp = [[0] * 4 for _ in range(n)]
        dp[0][0] = -prices[0]

        for i in range(1,n):
            dp[i][0] = max(dp[i-1][0], dp[i-1][3] - prices[i], dp[i-1][1] - prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i-1][3])
            dp[i][2] = dp[i-1][0] + prices[i]
            dp[i][3] = dp[i-1][2]

        return max(dp[n-1][3], dp[n-1][1], dp[n-1][2])

714. Best Time to Buy and Sell Stock with Transaction Fee

Same with Problem 122, just add the transaction fee.

class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        n = len(prices)
        hold, free = [0] * n, [0] * n
        
        hold[0] = -prices[0]
        
        for i in range(1, n):
            hold[i] = max(hold[i - 1], free[i - 1] - prices[i])
            free[i] = max(free[i - 1], hold[i - 1] + prices[i] - fee)
        
        return free[-1]