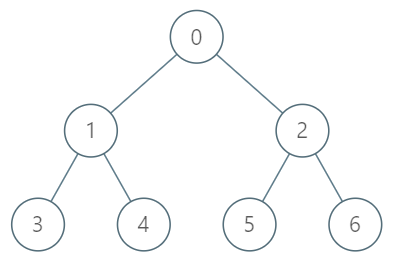
给你一棵树,树上有 n 个节点,按从 0 到 n-1 编号。树以父节点数组的形式给出,其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。
树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。
实现 TreeAncestor 类:
TreeAncestor(int n, int[] parent)对树和父数组中的节点数初始化对象。getKthAncestor(int node, int k)返回节点node的第k个祖先节点。如果不存在这样的祖先节点,返回-1。
示例 1:
输入: ["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"] [[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]] 输出: [null,1,0,-1] 解释: TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]); treeAncestor.getKthAncestor(3, 1); // 返回 1 ,它是 3 的父节点 treeAncestor.getKthAncestor(5, 2); // 返回 0 ,它是 5 的祖父节点 treeAncestor.getKthAncestor(6, 3); // 返回 -1 因为不存在满足要求的祖先节点
提示:
1 <= k <= n <= 5 * 104parent[0] == -1表示编号为0的节点是根节点。- 对于所有的
0 < i < n,0 <= parent[i] < n总成立 0 <= node < n- 至多查询
5 * 104次
方法一:动态规划 + 倍增
题目要我们寻找节点 node 的第 node 开始向上遍历
我们可以使用动态规划的思想,结合倍增的思想来处理。
我们定义
即:要想找到节点
之后对于每次查询,我们可以把
时间复杂度:初始化为
class TreeAncestor:
def __init__(self, n: int, parent: List[int]):
self.p = [[-1] * 18 for _ in range(n)]
for i, fa in enumerate(parent):
self.p[i][0] = fa
for i in range(n):
for j in range(1, 18):
if self.p[i][j - 1] == -1:
continue
self.p[i][j] = self.p[self.p[i][j - 1]][j - 1]
def getKthAncestor(self, node: int, k: int) -> int:
for i in range(17, -1, -1):
if k >> i & 1:
node = self.p[node][i]
if node == -1:
break
return node
# Your TreeAncestor object will be instantiated and called as such:
# obj = TreeAncestor(n, parent)
# param_1 = obj.getKthAncestor(node,k)class TreeAncestor {
private int[][] p;
public TreeAncestor(int n, int[] parent) {
p = new int[n][18];
for (var e : p) {
Arrays.fill(e, -1);
}
for (int i = 0; i < n; ++i) {
p[i][0] = parent[i];
}
for (int i = 0; i < n; ++i) {
for (int j = 1; j < 18; ++j) {
if (p[i][j - 1] == -1) {
continue;
}
p[i][j] = p[p[i][j - 1]][j - 1];
}
}
}
public int getKthAncestor(int node, int k) {
for (int i = 17; i >= 0; --i) {
if (((k >> i) & 1) == 1) {
node = p[node][i];
if (node == -1) {
break;
}
}
}
return node;
}
}
/**
* Your TreeAncestor object will be instantiated and called as such:
* TreeAncestor obj = new TreeAncestor(n, parent);
* int param_1 = obj.getKthAncestor(node,k);
*/class TreeAncestor {
public:
TreeAncestor(int n, vector<int>& parent) {
p = vector<vector<int>>(n, vector<int>(18, -1));
for (int i = 0; i < n; ++i) {
p[i][0] = parent[i];
}
for (int i = 0; i < n; ++i) {
for (int j = 1; j < 18; ++j) {
if (p[i][j - 1] == -1) {
continue;
}
p[i][j] = p[p[i][j - 1]][j - 1];
}
}
}
int getKthAncestor(int node, int k) {
for (int i = 17; ~i; --i) {
if (k >> i & 1) {
node = p[node][i];
if (node == -1) {
break;
}
}
}
return node;
}
private:
vector<vector<int>> p;
};
/**
* Your TreeAncestor object will be instantiated and called as such:
* TreeAncestor* obj = new TreeAncestor(n, parent);
* int param_1 = obj->getKthAncestor(node,k);
*/type TreeAncestor struct {
p [][18]int
}
func Constructor(n int, parent []int) TreeAncestor {
p := make([][18]int, n)
for i, fa := range parent {
p[i][0] = fa
for j := 1; j < 18; j++ {
p[i][j] = -1
}
}
for i := range p {
for j := 1; j < 18; j++ {
if p[i][j-1] == -1 {
continue
}
p[i][j] = p[p[i][j-1]][j-1]
}
}
return TreeAncestor{p}
}
func (this *TreeAncestor) GetKthAncestor(node int, k int) int {
for i := 17; i >= 0; i-- {
if k>>i&1 == 1 {
node = this.p[node][i]
if node == -1 {
break
}
}
}
return node
}
/**
* Your TreeAncestor object will be instantiated and called as such:
* obj := Constructor(n, parent);
* param_1 := obj.GetKthAncestor(node,k);
*/