README.md

1504. 统计全 1 子矩形

English Version

题目描述

给你一个 m x n 的二进制矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。

 

示例 1：

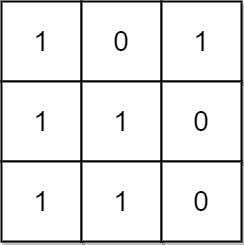
输入：mat = [[1,0,1],[1,1,0],[1,1,0]]
输出：13
解释：
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。

示例 2：

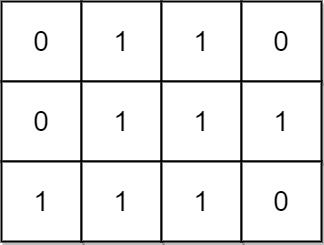
输入：mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]
输出：24
解释：
有 8 个 1x1 的子矩形。
有 5 个 1x2 的子矩形。
有 2 个 1x3 的子矩形。
有 4 个 2x1 的子矩形。
有 2 个 2x2 的子矩形。
有 2 个 3x1 的子矩形。
有 1 个 3x2 的子矩形。
矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。

 

提示：

• 1 <= m, n <= 150
• mat[i][j] 仅包含 0 或 1

解法

方法一：枚举 + 前缀和

我们可以枚举矩阵的右下角 $(i, j)$，然后向上枚举矩阵的第一行 $k$，那么每一行以 $(i, j)$ 为右下角的矩阵的宽度就是 $\min_{k \leq i} \textit{g}[k][j]$，其中 $\textit{g}[k][j]$ 表示第 $k$ 行以 $(k, j)$ 为右下角的矩阵的宽度。

因此，我们可以预处理得到二维数组 $g[i][j]$，其中 $g[i][j]$ 表示第 $i$ 行中，从第 $j$ 列向左连续的 $1$ 的个数。

时间复杂度 $O(m^2 \times n)$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别是矩阵的行数和列数。

Python3

class Solution:
    def numSubmat(self, mat: List[List[int]]) -> int:
        m, n = len(mat), len(mat[0])
        g = [[0] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                if mat[i][j]:
                    g[i][j] = 1 if j == 0 else 1 + g[i][j - 1]
        ans = 0
        for i in range(m):
            for j in range(n):
                col = inf
                for k in range(i, -1, -1):
                    col = min(col, g[k][j])
                    ans += col
        return ans

Java

class Solution {
    public int numSubmat(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[][] g = new int[m][n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 1) {
                    g[i][j] = j == 0 ? 1 : 1 + g[i][j - 1];
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int col = 1 << 30;
                for (int k = i; k >= 0 && col > 0; --k) {
                    col = Math.min(col, g[k][j]);
                    ans += col;
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int numSubmat(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> g(m, vector<int>(n));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 1) {
                    g[i][j] = j == 0 ? 1 : 1 + g[i][j - 1];
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int col = 1 << 30;
                for (int k = i; k >= 0 && col > 0; --k) {
                    col = min(col, g[k][j]);
                    ans += col;
                }
            }
        }
        return ans;
    }
};

Go

func numSubmat(mat [][]int) (ans int) {
	m, n := len(mat), len(mat[0])
	g := make([][]int, m)
	for i := range g {
		g[i] = make([]int, n)
		for j := range g[i] {
			if mat[i][j] == 1 {
				if j == 0 {
					g[i][j] = 1
				} else {
					g[i][j] = 1 + g[i][j-1]
				}
			}
		}
	}
	for i := range g {
		for j := range g[i] {
			col := 1 << 30
			for k := i; k >= 0 && col > 0; k-- {
				col = min(col, g[k][j])
				ans += col
			}
		}
	}
	return
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

...