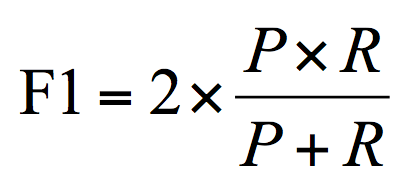问题
- 比例更小
- 危害更大
- 逻辑回归分类
- 二分类问题,什么模型评估更准确
- 实战项目
- 概念
逻辑回归
logistic 回归,它实际上是分类方法,为了解决二分类问题。也可解决多分类问题
- 函数公式
函数图形
-
z越大的时候,g(z)越大,当z趋近于无穷大的时候,g(z)趋近于1 -
z趋近于无穷小的时候,g(z)趋近于 0 -
函数值以
0.5为中心 -
0即为不发生,1即为发生
LogisticRegression()完整代码:
# -*- coding:utf-8 -*-
# 使用逻辑回归对信用卡欺诈进行分类
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import itertools
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, precision_recall_curve
from sklearn.preprocessing import StandardScaler
import warnings
warnings.filterwarnings('ignore')
# 混淆矩阵可视化
def plot_confusion_matrix(cm, classes, normalize=False, title='Confusion matrix"', cmap=plt.cm.Blues):
plt.figure()
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=0)
plt.yticks(tick_marks, classes)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment='center',
color='white' if cm[i, j] > thresh else 'black')
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
# 显示模型评估结果
def show_metrics():
tp = cm[1, 1]
fn = cm[1, 0]
fp = cm[0, 1]
tn = cm[0, 0]
print('精确率: {:.3f}'.format(tp / (tp + fp)))
print('召回率: {:.3f}'.format(tp / (tp + fn)))
print('F1值: {:.3f}'.format(2 * (((tp / (tp + fp)) * (tp / (tp + fn))) / ((tp / (tp + fp)) + (tp / (tp + fn))))))
# 绘制精确率-召回率曲线
def plot_precision_recall():
plt.step(recall, precision, color='b', alpha=0.2, where='post')
plt.fill_between(recall, precision, step='post', alpha=0.2, color='b')
plt.plot(recall, precision, linewidth=2)
plt.xlim([0.0, 1])
plt.ylim([0.0, 1.05])
plt.xlabel('召回率')
plt.ylabel('精确率')
plt.title('精确率-召回率 曲线')
plt.show();
# 数据加载
data = pd.read_csv('./creditcard.csv')
# 数据探索
print(data.describe())
# 设置plt正确显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
# 绘制类别分布
plt.figure()
ax = sns.countplot(x='Class', data=data)
plt.title('类别分布')
plt.show()
# 显示交易笔数,欺诈交易笔数
num = len(data)
num_fraud = len(data[data['Class'] == 1])
print('总交易笔数: ', num)
print('诈骗交易笔数:', num_fraud)
print('诈骗交易比例:{:.6f}'.format(num_fraud / num))
# 欺诈和正常交易可视化
f, (ax1, ax2) = plt.subplots(2, 1, sharex=True, figsize=(15, 8))
bins = 50
ax1.hist(data.Time[data.Class == 1], bins=bins, color='deeppink')
ax1.set_title('诈骗交易')
ax2.hist(data.Time[data.Class == 0], bins=bins, color='deepskyblue')
ax2.set_title('正常交易')
plt.xlabel('时间')
plt.ylabel('交易次数')
plt.show()
# 对Amount进行数据规范化
data['Amount_Norm'] = StandardScaler().fit_transform(data['Amount'].values.reshape(-1, 1))
# 特征选择
y = np.array(data.Class.tolist())
data = data.drop(['Time', 'Amount', 'Class'], axis=1)
X = np.array(data.as_matrix())
# 准备训练集和测试集
train_x, test_x, train_y, test_y = train_test_split(X, y, test_size=0.1, random_state=33)
# 逻辑回归分类
clf = LogisticRegression()
clf.fit(train_x, train_y)
predict_y = clf.predict(test_x)
# 预测样本的置信分数
score_y = clf.decision_function(test_x)
# 计算混淆矩阵,并显示
cm = confusion_matrix(test_y, predict_y)
class_names = [0, 1]
# 显示混淆矩阵
plot_confusion_matrix(cm, classes=class_names, title='逻辑回归 混淆矩阵')
# 显示模型评估分数
show_metrics()
# 计算精确确率,召回率,阈值用于可视化
precision, recall, thresholds = precision_recall_curve(test_y, score_y)
plot_precision_recall()参数:
penalty:惩罚项,取值为 l1 或 l2,默认为 l2...solver:代表的是逻辑回归损失函数的优化方法max_iter:算法收敛的最大迭代次数n_jobs:拟合和预测的时候 CPU 的核数,默认是 1
模型评估指标
评估模型的好坏
F1
F1 作为精确率 P 和召回率 R 的调和平均
数值越大代表模型的结果越好
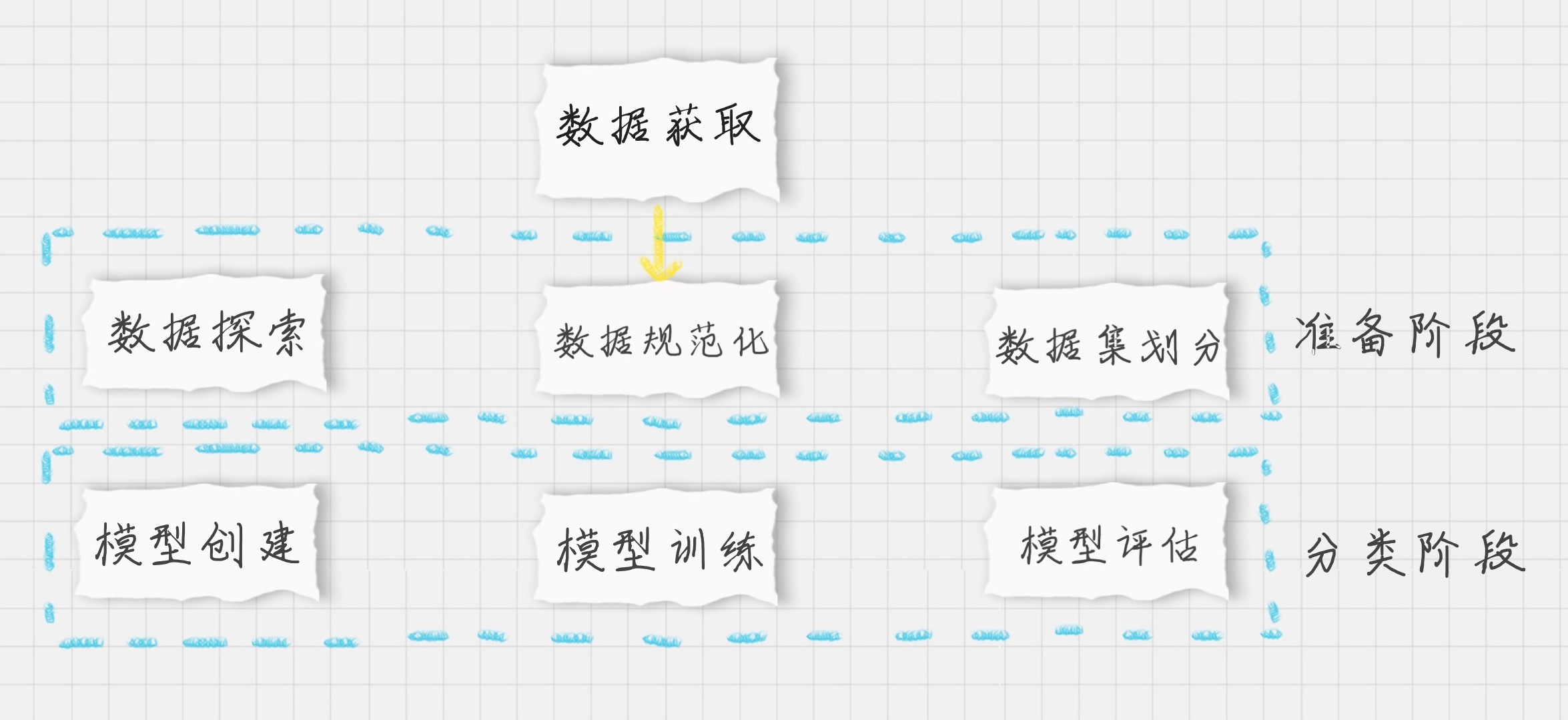
分析步骤
总量
诈骗交易 && 正常交易
总交易笔数: 284807
诈骗交易笔数: 492
诈骗交易比例:0.001727
逻辑回归 混淆矩阵
精准率 召回率
混淆矩阵
混淆矩阵也叫误差矩阵,实际上它就是 TP、FP、TN、FN 这四个数值的矩阵表示
precision_recall_curve 函数,预测值和真实值来计算精确率 - 召回率曲线
precision_recall_curve 函数会计算在不同概率阈值情况下的精确率和召回率