当时把一些刷题技巧整理成了模板,准备带去机试的,但是考前通知不让带了(2019年)
很多刷北邮OJ的题解都放在上面,其他OJ平台的题解也有一些
https://vpn.bupt.edu.cn/http/10.105.242.80/problem/p/101/
我们都学过计算机网络,了解IPV4地址的点分十进制表示法。
你的任务很简单:判断一个字符串是否是一个合法的点分十进制表示的IPV4地址。
最低的IP地址是0.0.0.0,最高的IP地址是255.255.255.255。
PS :方便起见,认为形似00.00.00.00的IP地址也是合法的。
第一行是一个整数T,代表输入还剩下T行
以下的T行,每行都是一个字符串(不含空白字符)。字符串的长度保证不超过15,不小于1.
输出格式
对于每个字符串,输出一行。
如果它是一个合法的IPV4地址,输出Yes。
否则,输出No。
3
59.64.130.18
f.a.t.e
1.23.45.678
Yes
No
No
我编写了一个专用的split函数。但是要特判123.123.123.123.这样的情况
#include <bits/stdc++.h>
#define FF(a,b) for(int a=0;a<b;a++)
#define F(a,b) for(int a=1;a<=b;a++)
#define LEN 100
#define INF 1000000
#define bug(x) cout<<#x<<"="<<x<<endl;
using namespace std;
typedef long long ll;
void split(string s,char splitchar,vector<string>& vec)
{
int L = s.length();
int start=0;
string topush;
for(int i=0; i<L; i++)
{
if(s[i] == splitchar && i == 0)//第一个就遇到分割符
{
start += 1;
}
else if(s[i] == splitchar)
{
topush=s.substr(start,i - start);
if(topush.length()>0)
vec.push_back(topush);
start = i+1;
}
else if(i == L-1)//到达尾部
{
topush=s.substr(start,i+1 - start);
if(topush.length()>0)
vec.push_back(topush);
}
}
}
bool isDigit(string str){
if(str.length()==0) return 0;
FF(i,str.length()){
if(str[i]>'9' || str[i]<'0')
return 0;
}
return 1;
}
bool valid(string str){
int num;
sscanf(str.c_str(),"%d",&num);
if(num<0 || num>255)
return 0;
return 1;
}
int main()
{
// freopen("./in","r",stdin);
int T;
scanf("%d",&T);
char buf[1000];
getchar();
while(T--){
gets(buf);
vector<string> v;
split(string(buf),'.',v);
bool Yes=0;
if(v.size()==4 && buf[strlen(buf)-1]!='.'){
Yes=1;
FF(i,4){
if((!isDigit(v[i])) || (!valid(v[i]) )){
Yes=0;
break;
}
}
}
puts(Yes?"Yes":"No");
}
return 0;
}
https://vpn.bupt.edu.cn/http/10.105.242.80/problem/p/103/
对于这种题要引起重视了
#include <bits/stdc++.h>
#define FF(a,b) for(int a=0;a<b;a++)
#define F(a,b) for(int a=1;a<=b;a++)
#define LEN 100
#define INF 1000000
#define bug(x) cout<<#x<<"="<<x<<endl;
using namespace std;
typedef long long ll;
const double pi=acos(-1);
char buf[1010];
int main()
{
// freopen("./in","r",stdin);
ios::sync_with_stdio(false);//这东西开了,stdio的东西都别想用了
string s;
vector<string> v;
while(cin>>s){
v.clear();
v.push_back(s);
while(1){
// char c=getchar();
char c=cin.get();//老老实实用这个,上一行读出来的都是EOF
if(c=='\n' || c==EOF)
break;
cin>>s;
v.push_back(s);
}
reverse(v.begin(),v.end());
FF(i,v.size()){
cout<<v[i];
if(i!=v.size()-1)
cout<<' ';
}
cout<<endl;
}
return 0;
}
https://vpn.bupt.edu.cn/http/10.105.242.80/problem/p/98/
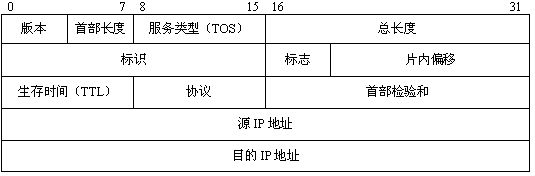
我们都学习过计算机网络,知道网络层IP协议数据包的头部格式如下:
其中IHL表示IP头的长度,单位是4字节;总长表示整个数据包的长度,单位是1字节。
传输层的TCP协议数据段的头部格式如下:
头部长度单位为4字节。
你的任务是,简要分析输入数据中的若干个TCP数据段的头部。 详细要求请见输入输出部分的说明。
第一行为一个整数T,代表测试数据的组数。
以下有T行,每行都是一个TCP数据包的头部分,字节用16进制表示,以空格隔开。数据保证字节之间仅有一个空格,且行首行尾没有多余的空白字符。
保证输入数据都是合法的。
对于每个TCP数据包,输出如下信息:
Case #x,x是当前测试数据的序号,从1开始。
Total length = L bytes,L是整个IP数据包的长度,单位是1字节。
Source = xxx.xxx.xxx.xxx,用点分十进制输出源IP地址。输入数据中不存在IPV6数据分组。
Destination = xxx.xxx.xxx.xxx,用点分十进制输出源IP地址。输入数据中不存在IPV6数据分组。
Source Port = sp,sp是源端口号。
Destination Port = dp,dp是目标端口号。
对于每个TCP数据包,最后输出一个多余的空白行。
具体格式参见样例。
请注意,输出的信息中,所有的空格、大小写、点符号、换行均要与样例格式保持一致,并且不要在任何数字前输出多余的前导0,也不要输出任何不必要的空白字符。
输入样例
2
45 00 00 34 7a 67 40 00 40 06 63 5a 0a cd 0a f4 7d 38 ca 09 cd f6 00 50 b4 d7 ae 1c 9b cf f2 40 80 10 ff 3d fd d0 00 00 01 01 08 0a 32 53 7d fb 5e 49 4e c8
45 00 00 c6 56 5a 40 00 34 06 e0 45 cb d0 2e 01 0a cd 0a f4 00 50 ce 61 e1 e9 b9 ee 47 c7 37 34 80 18 00 b5 81 8f 00 00 01 01 08 0a 88 24 fa c6 32 63 cd 8d
Case #1
Total length = 52 bytes
Source = 10.205.10.244
Destination = 125.56.202.9
Source Port = 52726
Destination Port = 80
Case #2
Total length = 198 bytes
Source = 203.208.46.1
Destination = 10.205.10.244
Source Port = 80
Destination Port = 52833
- IP头部
- TCP头部
45 00 00 34 //0034表示总长度, 即52B, 5表示首部长度, 5*4B
7a 67 40 00
40 06 63 5a
0a cd 0a f4 //源地址 10.205.10.244
7d 38 ca 09 //目的地址 125.56.202.9
cd f6 00 50 //源端口, 目的端口
b4 d7 ae 1c
9b cf f2 40
80 10 ff 3d
fd d0 00 00
Case #1
Total length = 52 bytes
Source = 10.205.10.244
Destination = 125.56.202.9
Source Port = 52726
Destination Port = 80
有点意思, 码量较大
需要训练做模拟题的速度
#include <bits/stdc++.h>
#define FF(a,b) for(int a=0;a<b;a++)
#define F(a,b) for(int a=1;a<=b;a++)
#define LEN 100
#define INF 1000000
#define bug(x) cout<<#x<<"="<<x<<endl;
using namespace std;
typedef long long ll;
char buf[1000];
char str[100][10];
int hex2int(char ch){
if(ch>='a'){
return ch-'a'+10;
}else{
return ch-'0';
}
}
int hex2int(char *ch){
int n=strlen(ch);
int ans=0;
int base=1;
for(int i=n-1,j=0
;i>=0;
i--,j++) //脑子秀逗了, 其实写个单循环就好了
{
ans+=hex2int(ch[i])*base;
base*=16;
}
return ans;
}
int main()
{
// freopen("./in","r",stdin);
int N;
scanf("%d",&N);
FF(i,N){
//gets(buf); 可以用gets读入带空格的一行
int n=0;
while(1){
scanf("%s",str[n++]);
char pd=getchar();
if(pd=='\n' || pd==EOF)
break;
}
int IPlen=hex2int(str[0][1]);
strcat(str[2],str[3]);
int TOTlen=hex2int(str[2]);
printf("Case #%d\n",i+1);
printf("Total length = %d bytes\n",TOTlen);
printf("Source = %d.%d.%d.%d\n",hex2int(str[12]),hex2int(str[13]),hex2int(str[14]),hex2int(str[15]));
printf("Destination = %d.%d.%d.%d\n",hex2int(str[16]),hex2int(str[17]),hex2int(str[18]),hex2int(str[19]));
strcat(str[IPlen*4],str[IPlen*4+1]);
strcat(str[IPlen*4+2],str[IPlen*4+3]);
printf("Source Port = %d\n",hex2int(str[IPlen*4]));
printf("Destination Port = %d\n",hex2int(str[IPlen*4+2]));
puts("");
}
return 0;
}
//Case #1
//Total length = 52 bytes
//Source = 10.205.10.244
//Destination = 125.56.202.9
//Source Port = 52726
//Destination Port = 80
给一棵树,你可以把其中任意一个节点作为根节点。每个节点都有一个小写字母,中序遍历,得到一个字符串,求所有能得到的字符串的字典序最小串。因为这棵树不一定是二叉树,所以中序遍历时,先中序遍历以节点序号最小的节点为根的子树,然后再遍历根节点,最后根据节点序号从小到大依次中序遍历剩下的子树。
- HINT
意思就是请枚举所有的点为根,然后中序遍历
最后输出所有结果中字典序最小的
比如说第二组数据
以0为根时结果为 bacd
以1为根时结果为 cadb
以2为根时结果为 badc
以3为根时结果为 bacd
所以字典序最小的是bacd
多组数据,以EOF结束。
第一行一个数n(0<n<=100),表示树的节点的个数,节点从0开始。
然后一个长度为n的串,第i(0<=i<n)个字符表示节点i的字符。
接下来n-1行,每行两个数a,b,(0<=a,b<n),表示a和b之间有一条无向边。
题中要求的最小的字符串
3
bac
0 1
1 2
4
abcd
0 1
0 2
0 3
bac
bacd
https://vpn.bupt.edu.cn/http/10.105.242.80/problem/p/109/
不难的一题,但写了贼久。。。
题设中序遍历步骤:
-
中序遍历(第
1个子节点) -
访问根节点
-
中序遍历(第
2...N子节点)
看起来很简单,但是遇到了以下坑。
-
必须要设置访问标记,否则直接访问父结点形成死循环
-
必须首先置根结点已访问
(A) -
要对子节点向量进行排序
-
对于寻找第一棵左子树,必须要参照
(B)进行循环,而不能简单的访问g[r][0] -
对于寻找根结点的遍历中,每次使用中序遍历之前,要对vis进行初始化
(C)
写了半天连样例都过不了.. ..要引起重视了
#include <bits/stdc++.h>
#define FF(a,b) for(int a=0;a<b;a++)
#define F(a,b) for(int a=1;a<=b;a++)
#define LEN 100
#define INF 1000000
#define bug(x) cout<<#x<<"="<<x<<endl;
using namespace std;
typedef long long ll;
const double pi=acos(-1);
vector<int> g[110];
int N;
string seq;
char s[110];
int vis[110];
int visit(int r){
seq+=s[r];
vis[r]=1;
}
void inorder(int r){
if(vis[r]) return;
vis[r]=1; //必须首先置根结点已访问(A)
if(g[r].size()){
sort(g[r].begin(),g[r].end());
int sz=g[r].size();
int i,to;
for(i=0;i<sz;i++){ //找到左子树(B)
to=g[r][i];
if(vis[to]) continue;
break;
}
if(i==sz) visit(r);
else{
inorder(to);//左子树
visit(r);
for(i++;i<sz;i++)
inorder(g[r][i]);
}
}else{
visit(r);
}
}
void inorder_travel(int r){
memset(vis,0,sizeof vis); //(C)
seq="";inorder(r);
}
int main()
{
// freopen("./in","r",stdin);
int a,b;
while(scanf("%d",&N)>0){
scanf("%s",s);
FF(i,N) g[i].clear();
memset(vis,0,sizeof vis);
FF(i,N-1){
scanf("%d%d",&a,&b);
g[a].push_back(b);
g[b].push_back(a);
}
inorder_travel(0);
string minSeq=seq;
for(int i=1;i<N;i++){
inorder_travel(i);
if(seq.length()!=N) continue;
if(seq<minSeq){
minSeq=seq;
}
}
printf("%s\n",minSeq.c_str());
}
return 0;
}
参考:https://blog.csdn.net/u012662688/article/details/50898476
正义的伙伴褋祈和葬仪社的机器人Fuyuneru正在被邪恶的GHQ部队追杀。眼看着快要逃不掉了,祈就把重要的东西塞到了机器人体内,让它先跑,自己吸引火力。
假设Fuyuneru带上东西开始逃跑时所处的点为原点,朝向为正北。操纵FuyuNeru的指令有如下四种:
right X: X是1-359之间的整数,Fuyuneru的前进方向顺时针转X度。
left X: X是1-359之间的整数,Fuyuneru的前进方向逆时针转X度。
forward X: X是整数(0<=X<=1000),Fuyuneru向当前朝向前进X米。
backward X: X是整数(0<=X<=1000),Fuyuneru向当前朝向后退X米。
现在祈向Fuyuneru体内输入了N(1<=N<=50)个这样的指令。可是由于此前Fuyuneru被GHQ部队击中,它出了一点小问题:这N个指令执行的顺序是不确定的。
问:Fuyuneru最远可能逃出多远?
即,Fuyuneru在执行完N条指令之后,距离原点最远的可能距离是多少?
输入格式
第一行是一个整数T,代表测试数据有T组。
每组测试数据中,第一行是一个整数N,代表指令有N条;
随后紧跟N行,每一行代表一个指令(格式保证是上述四种中的一种,数据保证合法)
对于每组数据,输出一行:最远的可能逃亡距离,精确到小数点后3位。
3
3
forward 100
backward 100
left 90
4
left 45
forward 100
right 45
forward 100
6
left 10
forward 40
right 30
left 10
backward 4
forward 4
141.421
200.000
40.585
#include <bits/stdc++.h>
#define FF(a,b) for(int a=0;a<b;a++)
#define F(a,b) for(int a=1;a<=b;a++)
#define LEN 100
#define INF 1000000
#define bug(x) cout<<#x<<"="<<x<<endl;
using namespace std;
typedef long long ll;
const double pi=acos(-1);
int main()
{
// freopen("./in","r",stdin);
int T,N;
char op[10];
int d;
scanf("%d",&T);
while(T--){
scanf("%d",&N);
int f=0,b=0;
vector<int> angle;
while(N--){
scanf("%s",op);
scanf("%d",&d);
switch(op[0]){
case 'f':
f+=d;
break;
case 'b':
b+=d;
break;
case 'l':
angle.push_back(360-d);
break;
case 'r':
angle.push_back(d);
break;
}
}
set<int> rec; //必须用set去重做记录,否则内存超限
//记录所有可能的角度组合
FF(i,angle.size()){ //对所有角度进行遍历
vector<int> tmp(rec.begin(),rec.end());
int sz=rec.size();
FF(j,sz) { //已记录角度
//对所有角度进行相加
rec.insert((tmp[j]+angle[i])%360);
}
//放入当前角度
rec.insert(angle[i]);
}
int minA=180;
set<int>::iterator it=rec.begin();
while(it!=rec.end()){
int a= *it;
int delta=abs(a-180);
minA=min(delta,minA);
it++;
}
double A=f,B=b;
double rad=((180.-minA)/180.)*pi;
double ans=sqrt(A*A+B*B-2*A*B*cos(rad));
printf("%.3f\n",ans);
}
return 0;
}
给定一个由小写字母a到z组成的字符串S,其中第i个字符为S[i](下标从0开始)。你需要完成下面两个操作:
INSERT c
其中c是一个待输入的字符。你需要在字符串的末尾添加这个字符。保证输入的字符同样是a到z之间的一个小写字母。
QUERY x
其中x是一个输入的整数下标。对于这个询问,你需要回答在S当中和S[x]相等且与x最近的距离。输入保证x在当前字符串中合法。
例如S = "abcaba",如果我们操作:
INSERT a
则在S的末端加一个字符a,S变成"abcabaa"。
接下来操作
QUERY 0
由于S[0] = a,在S中出现的离他最近的a在下标为3的位置上,距离为3 - 0 = 3。因此应当输出3。
接下来,如果
QUERY 4
S[4] = b,S中离它最近的b出现在下标为1处,距离为4 - 1 = 3。同样应当输出3。
给定初始字符串S和若干操作,对于每个QUERY,你需要求出相应的距离。
HINT 由于输入数据较大,C/C++中推荐使用scanf进行读入以获得更快的读入速度。同时请注意算法复杂度。
输入的第一行是一个正整数T(T≤20),表示测试数据的组数。
每组输入数据的第一行是一个初始串S。第二行是一个正整数m(1≤m≤100000),表示总共操作的数量。接下来m行,每行表示一个操作。操作的格式如上所述。
数据保证在任何情况下,S的长度不会超过100000。
对于每个QUERY,输出所求的最小距离。如果S中其它位置都不存在和它相同的字符,输出-1。
2
axb
3
INSERT a
QUERY 0
QUERY 1
explore
3
INSERT r
QUERY 7
QUERY 1
3
-1
2
-1
https://vpn.bupt.edu.cn/http/10.105.242.80/problem/p/94/
用set大法写了一堆自己都看不懂的代码, 一提交居然AC了, 一发入魂
#include <bits/stdc++.h>
#define FF(a,b) for(int a=0;a<b;a++)
#define F(a,b) for(int a=1;a<=b;a++)
#define LEN 510000
#define INF 1000000
#define bug(x) cout<<#x<<"="<<x<<endl;
using namespace std;
char buf[100010];
int main()
{
// freopen("./in","r",stdin);
int N;
scanf("%d",&N);
while(N--){
scanf("%s",buf);
int n;
scanf("%d",&n);
int len=strlen(buf);
set<int> pos[26]; //记录某一字母所在的所有位置
FF(i,len){
pos[buf[i]-'a'].insert(i);
}
while(n--){
char op[20];
char data[20];
scanf("%s%s",op,data);
if(strcmp(op,"INSERT")==0){
buf[len]=data[0];
pos[buf[len]-'a'].insert(len);//维护
len++;
buf[len]=0;
}else{
int p;
int ans;
sscanf(data,"%d",&p);
char c=buf[p];
set<int>& tpos=pos[c-'a'];
set<int>::iterator it=tpos.find(p);
if(it==tpos.end()){ //找不到
ans=-1;
}
else if(tpos.size()==1){ //只记录了找到的一个
ans=-1;
}
else{
it++;
ans=INF;
if(it!=tpos.end()){
ans=*it-p;
}
it--;//复原
if(it!=tpos.begin()){
it--;
if( (p-*it)<ans){
ans=(p-*it);
}
}
}
printf("%d\n",ans);
}
}
}
return 0;
}
其实DP也简单.
对于录入的数据, 从左到有做如下状态转移:
-
用pre[k] 记录 字母k最近(最靠右)出现的下标. 未出现用0代替
-
对字符串从左到右扫描, 当前下标为i , 字符为k, 做判断 :
- 如果pre[k]首次出现
pre[k] = i; //仅仅做更新
- 如果pre[k]不是首次出现
j=pre[k] //记录上次位置
pre[k] = i; //做更新
f[i]=i-j; //因为i是最近(右)出现的, 必然距离左边的那个字母最近
f[j]=min(f[j],f[i]) //而左边的, 需要状态转移
欧阳巨佬代码:
/*省略了头文件和预定义,不能运行,看看逻辑就行*/
int T;
char s[N], ss[N];
int q;
char c;
int n;
int f[N];
int pre[N];
void wk(int i) {
f[i] = inf;
int k=s[i] - 'a';
int j = pre[k];
if (!pre[k])
pre[k] = i;
else {
f[i] = i - j;
pre[k] = i;
f[j]=min(f[j],i-j);
}
}
void wk2(int i) { //这个是我阅读巨佬代码后做的优化, 减少代码量, 逻辑与wk等效
f[i] = inf;
int k=s[i] - 'a';
int j = pre[k];
if(pre[k]) {
f[i] = i - j;
f[j]=min(f[j],i-j);
}
pre[k] = i;
}
signed main()
{
freopen("in","r",stdin);
sdf(T);
while (T--) {
scanf("%s", s + 1);
n = strlen(s + 1);
sdf(q);
For(i, 0, 25)pre[i] = 0;
For(i, 1, n) {
wk(i);
}
while (q--) {
scanf("%s", ss + 1);
if (ss[1] == 'I') {
scanf(" %c", &c);
s[++n] = c;
wk(n);
} else {
int x;
sdf(x);
x++;
if (f[x] == inf)printf("-1\n");
else printf("%lld\n", f[x]);
}
}
}
}
考虑等式:
x^2 + s(x)·x - n = 0,
其中x,n是正整数,s(x)是个函数,其值等于x在十进制下所有数字的和。
现给出整数n的大小,请你求出最小的满足条件的正整数x。
输入仅包含一个整数n (1 ≤ n ≤ 1018) .
输出格式
如果不存在这样的x,请输出-1;否则请输出满足条件的最小的整数x (x > 0)
2
1
#include <bits/stdc++.h>
#define FF(a,b) for(int a=0;a<b;a++)
#define F(a,b) for(int a=1;a<=b;a++)
#define LEN 100
#define INF 1000000
#define bug(x) cout<<#x<<"="<<x<<endl;
using namespace std;
typedef long long ll;
const double pi=acos(-1);
ll s(int x){
ll ans=0;
while(x){
ans+=x%10;
x/=10;
}
return ans;
}
int main()
{
// freopen("./in","r",stdin);
ll n,x,ans=-1,k;
cin>>n;
for(x=(ll)sqrt(n)+1,k=0;
x>=0 && k<18*9;
x--,k++){
if(x*x+x*s(x)==n){
ans=x;
break;
}
}
cout<<ans<<endl;
return 0;
}
https://vpn.bupt.edu.cn/http/10.105.242.80/problem/p/108/
给你一个复数集合{Aj+i*Bj},保证Aj和Bj都是整数,初始为空集。
每次会给你如下两种操作中的一种:
-
"Insert x+iy",其中x,y都是整数。表示在集合中加入一个复数 x+iy,同时输出此时集合的大小;
-
"Pop"。如果集合为空集直接返回"Empty!",如果有元素则以"x+iy"的形式显示集合中模值最大的复数,然后将该元素从集合中删除,之后在第二行显示操作之后的集合大小,如果为空集则显示"Empty!"。
-
第一行只有一个数T,代表case数。0<=T<=10
-
每一组case:
-
第一行有一个整数n,表示这组case中一共有n条命令 0<n<=100
-
接下来n行每行有一个命令,命令如上所述
保证不会输入两个模值同样的元素,并保证实部虚部都大于0,小于1000。
依照上述原则输出每一个命令对应的输出
如果输入命令是Insert命令,则对应的输出占一行为集合大小;
如果输入命令是Pop命令,则对应的输出占一行或者两行,为模值最大的复数和集合大小。
请注意,输出集合大小的格式为"Size:空格x回车",x为集合大小
1
5
Pop
Insert 1+i2
Insert 2+i3
Pop
Pop
Empty!
Size: 1
Size: 2
2+i3
Size: 1
1+i2
Empty!
看到本题要立刻想到用优先队列
牢记优先队列的运算符重载
/*
USER_ID: test#shizhuxiniubi
PROBLEM: 108
SUBMISSION_TIME: 2019-02-03 11:34:38
*/
#include <bits/stdc++.h>
#define FF(a,b) for(int a=0;a<b;a++)
#define F(a,b) for(int a=1;a<=b;a++)
#define LEN 100
#define INF 1000000
#define bug(x) cout<<#x<<"="<<x<<endl;
using namespace std;
typedef long long ll;
const double pi=acos(-1);
typedef struct Node{
int x,y;
double m;
Node(int x=0,int y=0):x(x),y(y){
m=sqrt(double(x*x+y*y));
}
void output(){
printf("%d+i%d\n",x,y);
}
void input(){
scanf("%d+i%d\n",&x,&y);
m=sqrt(double(x*x+y*y));
}
}Node;
struct cmp{
bool operator () (const Node& a,const Node& b){//大根堆
return a.m<b.m;
}
};
priority_queue<Node,vector<Node>,cmp> pq;//大根堆
void output_size(){
if(pq.size())
printf("Size: %d\n",pq.size());
else
puts("Empty!");
}
int main()
{
// freopen("./in","r",stdin);
int T,N;
char op[10];
scanf("%d",&T);
while(T--){
while(pq.size())//初始化.在这个地方wa了
pq.pop();
scanf("%d",&N);
while(N--){
scanf("%s",op);
if(op[0]=='P'){//Pop
if(pq.size()){
Node u=pq.top();
pq.pop();
u.output();
output_size();
}else puts("Empty!");
}else{
Node u;
u.input();
pq.push(u);
output_size();
}
}
}
return 0;
}