滑动窗口.md

滑动窗口

模板

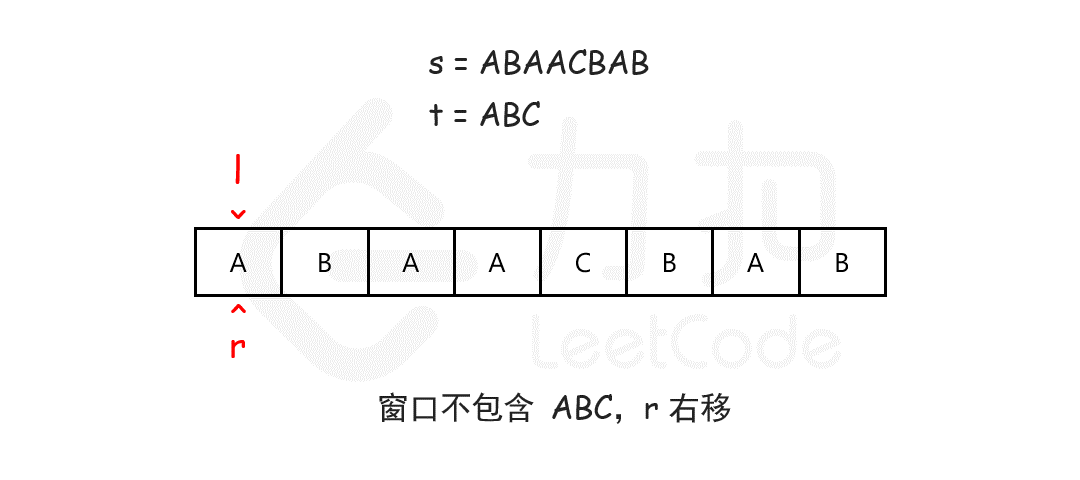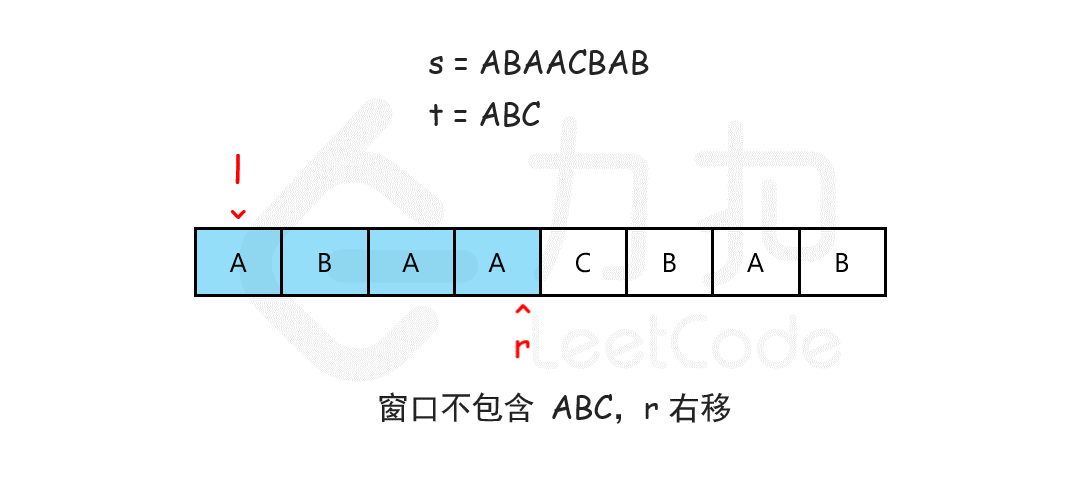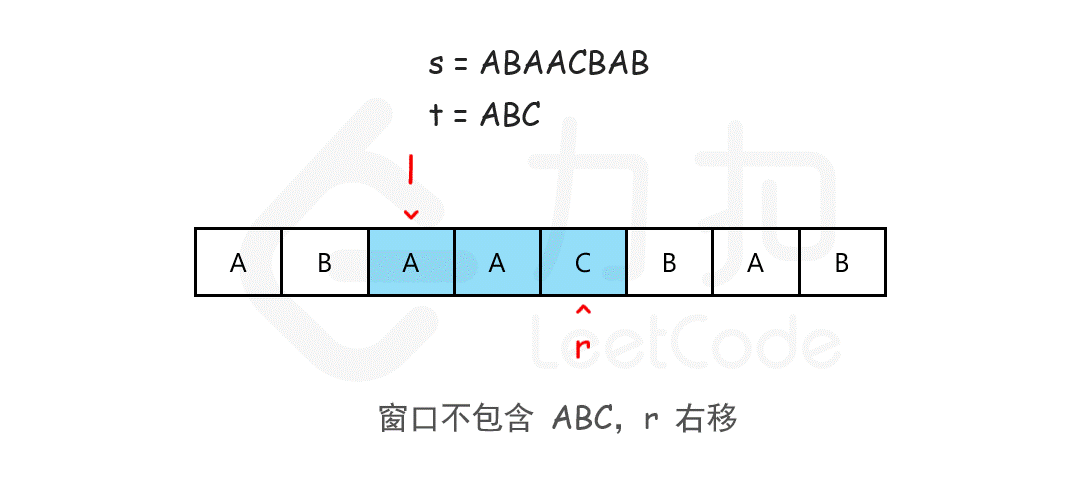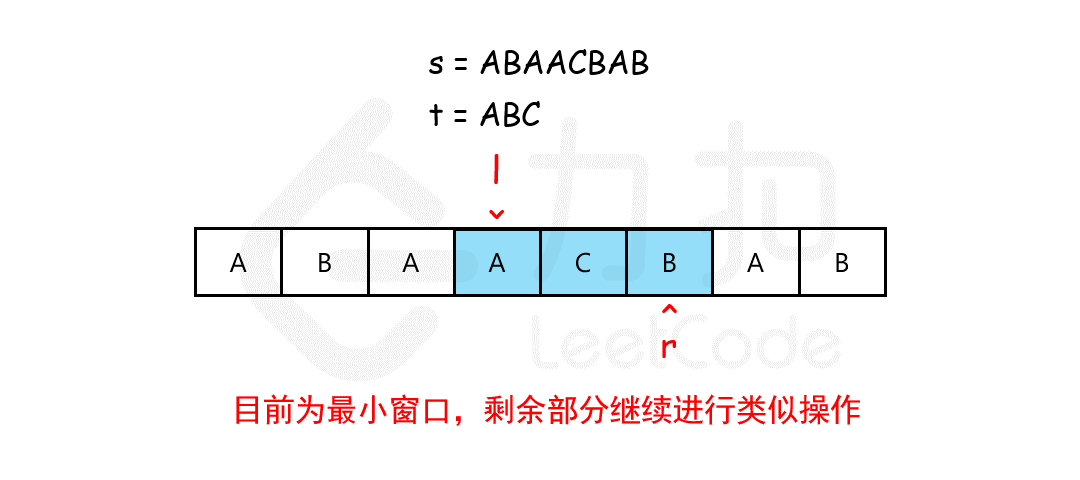
/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/

        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

需要变化的地方

1. 右指针右移之后窗口数据更新
2. 判断窗口是否要收缩
3. 左指针右移之后窗口数据更新
4. 根据题意计算结果

例子

76. 最小覆盖子串

func minWindow(s string, t string) string {
    // 保存滑动窗口字符集
    win := make(map[byte]int)
    // 保存需要的字符集
    need := make(map[byte]int)

    for i := 0; i < len(t); i++ {
        need[t[i]]++
    }

    // windows
    left := 0
    right := 0

    match := 0
    start := 0
    end := 0
    min := math.MaxInt64
    
    for right < len(s) {
        c := s[right]
        right++
        
        // 在需要的字符集里面，添加到窗口字符集里面
        if need[c] != 0 {
            win[c]++
            if win[c] == need[c] {
                match++
            }
        }
        
        // 当所有自负数量都匹配之后，开始缩紧窗口
        for match == len(need) {
            if right - left < min {
                min = right - left
                start = left
                end = right
            }
            c = s[left]
            left++
            // 左指针指向不在需要字符集则直接跳过
            if need[c] != 0 {
                // 左指针指向字符数量和需要的字符相等时，右移之后match值就不匹配则减一
                // 因为win里面的字符数可能比较多，如有10个A，但需要的字符数量可能为3
                // 所以在压死骆驼的最后一根稻草时，match才减一，这时候才跳出循环
                if win[c] == need[c] {
                    match--
                }
                win[c]-- 
            }
        }
    }

    if min == math.MaxInt64 {
        return ""
    }
    return s[start:end]
}

567. 字符串的排列

func checkInclusion(s1 string, s2 string) bool {
    window := make(map[byte]int)
    need := make(map[byte]int)

    for i := 0; i < len(s1); i++ {
        need[s1[i]]++
    }

    left := 0
    right := 0
    match := 0

    for right < len(s2) {
        c := s2[right]
        right++

        if need[c] != 0 {
            window[c]++
            if window[c] == need[c] {
                match++
            }
        }

        for right - left >= len(s1) {
            if match == len(need) {
                return true
            }

            d := s2[left]
            left++
            
            if need[d] != 0 {
                if window[d] == need[d] {
                    match--
                }
                window[d]--
            }
        }
    }
    return false
}

438. 找到字符串中所有字母异位词

func findAnagrams(s string, p string) []int {
    window := make(map[byte]int)
    need := make(map[byte]int)

    for i := 0; i < len(p); i++ {
        need[p[i]]++
    }

    left := 0
    right := 0
    match := 0

    result := make([]int, 0)

    for right < len(s) {
        c := s[right]
        right++

        if need[c] != 0 {
            window[c]++
            if window[c] == need[c] {
                match++
            }
        }

        for right - left >= len(p) {
            if match == len(need) {
                result = append(result, left)
            }

            d := s[left]
            left++
            
            if need[d] != 0 {
                if window[d] == need[d] {
                    match--
                }
                window[d]--
            }
        }
    }
    return result
}