正如我们在上一章中所看到的,音乐信号通常是由多种不同声音成分组成的复杂声音混合物。由于这种复杂性,从波形中提取与音乐相关的信息成为了一个难题。要想更好地理解一个给定的信号,第一步是将其分解为后续步骤更容易处理的 组成部分(building blocks) 。如果这些组成部分由正弦函数组成,则这种过程也称为傅里叶分析。正弦函数的特殊之处在于,它们在频率方面具有明确的物理意义。因此,分解结果将信号的按频谱展开——类似于棱镜,可用于将光分解为其组成的光谱颜色。傅里叶变换将依赖于时间的信号转换为依赖于频率的表示。作为信号处理中最重要的工具之一,我们将在各种音乐处理任务中遇到傅里叶变换。
在第2.1节中,我们将介绍傅立叶变换的主要思想,并总结理解本书后续章节所需的最重要的一些事实。此外,我们还介绍了所需的数学概念。对第2.1节的充分理解对于本书后面将要讨论的各种音乐处理任务至关重要。在第2.2节至第2.5节中,我们将更深入地介绍傅里叶变换。只对音乐处理应用感兴趣的读者可以在第一次阅读本书时跳过这些技术性较强的部分。
在第2.2节中,我们将更仔细地考察信号,并从更抽象的角度讨论其特性。特别是,我们考虑两类信号:
- 模拟信号,它给我们正确的物理解释;
- 数字信号,需要计算机进行实际的数字处理。
不同的信号类别导致傅里叶变换的不同版本,我们以数学上的严谨性以及直观的解释和大量示例(第2.3节)介绍了傅里叶变换。特别是,我们解释了不同版本的傅里叶变换是如何相互关联的,以及如何通过 离散傅里叶变换(DFT) 来近似它们。可通过 快速傅里叶变换(FFT) 有效计算DFT,这将在第2.4节中讨论。最后,我们介绍 短时傅里叶变换(STFT) ,它是傅里叶变换的局部变体,可以用来产生信号的时频表示(第2.5节)。通过从工程课程中通常遇到的不同角度介绍这些材料,我们希望能够完善和提高对这些重要而美好概念的理解。
让我们从一些音乐的音频信号开始。例如,让我们分析在钢琴上弹奏的单个音符的声音(见图2.1a)。我们怎样才能知道到底演奏了哪个音符?回顾第1.3.2节,一个乐音的音调与其基频密切相关,而基频就是声音最低部分的频率。因此,我们需要确定频率的内容,即信号的主要周期振荡。让我们放大信号,仅考虑10ms部分(见图2.1b)。该图显示信号在该区域内以近似周期的方式运行。特别是,可以观察到正弦型振荡的三个主要波峰(见图2.1c)。在10ms段内有大约三个振荡周期意味着信号中包含大约为 $300Hz$ 的频率成分。
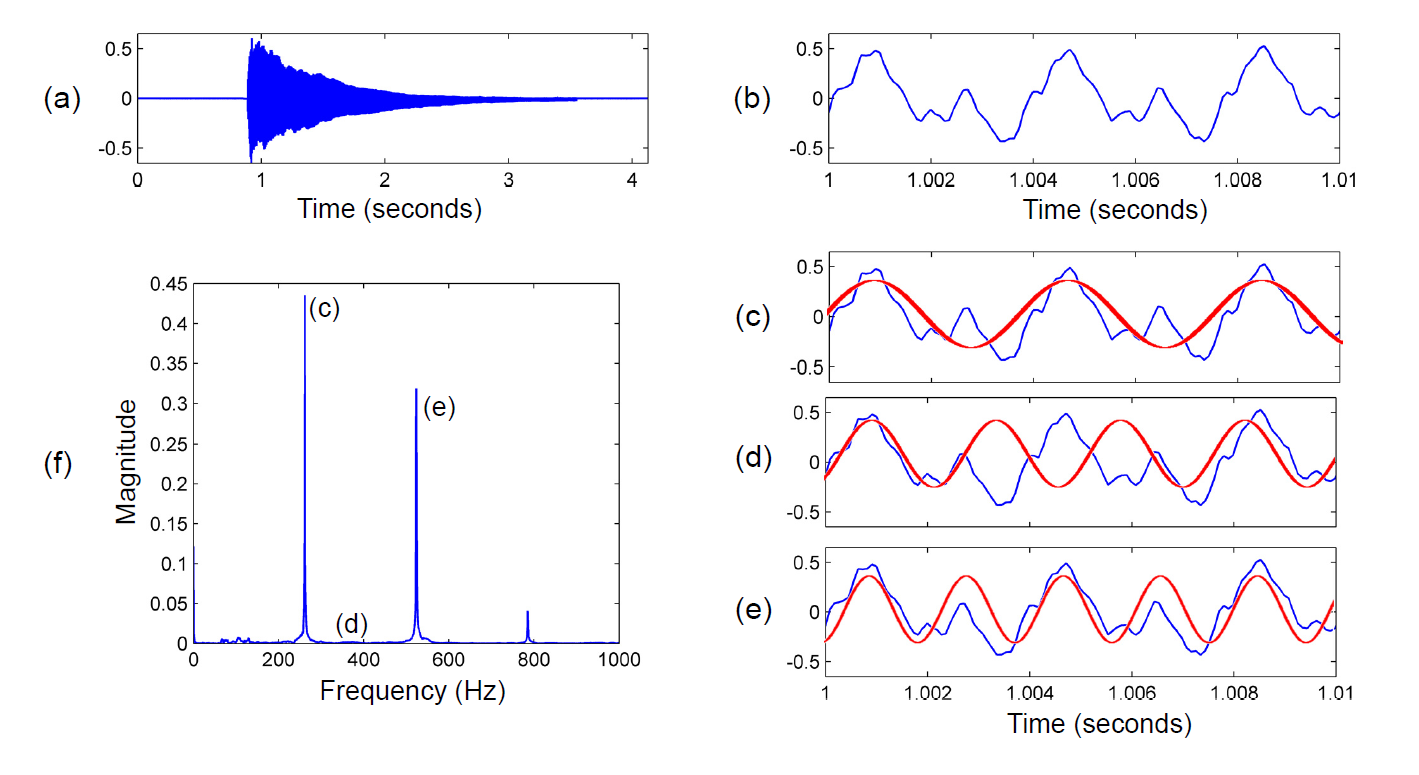 |
| 图2.1 (a)钢琴上弹奏的音符C4(261.6 Hz)的波形。(b)从t=1s开始的10ms的放大波形。(c–e)波形与不同频率的正弦波形$\omega$的比较。(f)取决于频率$\omega$的幅值系数$d_{\omega}$。 |
傅里叶分析(Fourier analysis) 的主要思想是将信号与不同频率 $\omega \in \mathbb{R}$ 的正弦波(以Hz为单位)进行比较。每一个这样的正弦波或纯音都可以被认为是一个 原型振荡(prototype oscillation) 。由此,对于任何一个频率 $\omega \in \mathbb{R}$ ,我们可以得到这个声音在这一频率上的幅值系数 $d_{\omega}\in\mathbb{R}{\ge0}$ (包括相位系数 $\varphi{\omega}\in\mathbb{R}$ ),我们后面后给出解释。在系数 $d_{\omega}$ 较大的情况下,声音信号与频率为 $\omega$ 的正弦波之间存在高度相似性,且信号包含该频率的周期性振荡(见图2.1c)。在 $d_{\omega}$ 很小的情况下,信号不包含该频率的周期性分量(见图2.1d)。
幅值系数(magnitude coefficient)
让我们绘制各种频率参数 $\omega \in \mathbb{R}$ 下的幅值系数$d_{\omega}$ 。这将生成图2.1f所示的图形。在该图中,我们可以发现,频率参数 $\omega=262Hz$ 时,幅值系数 $d_{\omega}$ 取到最大值,而 $\omega=262Hz$ 恰好是这段乐音的基频。通过式(1.1),计算出大致对应到音高 $p=60$ 或者说是音符C4的中心频率。事实上,这正是我们钢琴示例中演奏的音符。此外,如图2.1e所示,还可以观察到信号与频率 $\omega=523Hz$ 的正弦信号之间的高度相似性。这大致是音调C4的第二分音的频率。
回顾一下式(1.1)
$F_{pitch}(p) = 2^{\frac{p-69}{12}}\times 440$
为了简单表述,这里没有把作者原意翻译出来,其实应该是说用基频频率 $\omega=262 Hz$ ,而不是用使得幅值系数最大的那个频率,虽然在这个例子两者是一样的。这段就是用一个简单的例子告诉我们,可以通过对原始的钢琴的声音信号做一些变换,来推测演奏出这段声音信号的音符是哪一个。
通过这个例子,我们已经看到了 傅里叶变换(Fourier transform) 背后的主要思想。傅里叶变换将信号分解为其各频率分量。对于每个频率 $\omega\in\mathbb{R}$ ,傅里叶变换可以计算出一个系数 $d_{\omega}$ (和一个相位 $\varphi_{\omega}$ ),它告诉我们给定信号在多大程度上匹配该频率的正弦原型振荡。
傅里叶变换的一个重要特性是可以从系数 $d_{\omega}$ (连同系数 $\varphi_{\omega}$ )重构原始信号。为此,我们可以叠加所有可能频率的正弦波,每个频率由各自的系数 $d_{\omega}$ 加权(并由 $\varphi_{\omega}$ 移位)。这种加权叠加的方式也称为原始信号的 傅里叶表示(Fourier representation) 。原始信号和傅里叶变换包含相同数量的信息。然而,这些信息以不同的方式被呈现。原始信号显示跨时间的信息,而傅里叶变换显示跨频率的信息。正如哈伯德(Hubbard)所说,声音信号告诉我们某些音符何时播放,但隐藏了有关频率的信息。相反,音乐的傅里叶变换显示播放的音符(频率),但隐藏了有关何时播放音符的信息。
在下面的部分中,我们将更详细地了解傅里叶变换及其一些主要特性。
在第1.3.1节中,我们看到通过一个信号或声波可以产生一个函数,该函数将气压与特定位置的平均气压的偏差分配给每个时间点。让我们考虑一个 模拟信号(analog signal) 的情况,其中时间和振幅(或偏差)都是连续的实值参数。在这种情况下,可以将信号建模为函数 $f:\mathbb{R}\rightarrow\mathbb{R}$ ,它为每个时间点 $t\in\mathbb{R}$ 分配一个振幅值 $f(t)\in\mathbb{R}$ 。绘制随时间变化的振幅,可以得到与信号波形相对应的该函数图(见图1.17)。
函数(function)一词可能需要一些解释。在数学中,函数表示了一组输入元素和一组输出元素之间的关系,其中每个输入元素只与一个输出元素相关。例如,函数可以是多项式 $f:\mathbb{R}\rightarrow\mathbb{R}$ ,其为每个输入元素 $t\in\mathbb{R}$ 分配一个输出元素 $f(t)=t^{2} \in\mathbb{R}$ 。在这一点上,我们要强调的是,需要区分函数 $f$ 本身,以及在特定的输入元素 $t$ (也称为参数(argument))上的输出元素 $f(t)$ (也称为值(value))。换句话说,数学家以一种抽象的方式思考函数 $f$ ,在这种情况下,参数的符号或物理意义并不重要。与此相反,工程师通常喜欢强调输入参数的含义,且认为函数就是 $f(t)$ ,即使严格地说这只是函数的输出值。在这本书中,我们假设从一位数学家的观点出发来看待这个问题。
在本旁注之后,让我们转向对一个给定模拟信号 $f:\mathbb{R}\rightarrow\mathbb{R}$ 的频谱分析(spectral analysis)。如我们在介绍示例中所解释的,我们将声音信号 $f$ 与以正弦形式给出的原型振荡进行比较。在第1.3.2节和图1.19中,我们已经遇到了这样的正弦信号。从数学上讲,正弦曲线是一个函数 $g:\mathbb{R}\rightarrow\mathbb{R}$ ,定义为
$$
g(t):=A \sin(2 \pi(\omega t-\varphi)) \tag{2.1}
$$
对任意 $t\in\mathbb{R}$ 。参数 $A$ 对应于振幅(amplitude),参数 $\omega$ 对应于频率(frequency)(以Hz为单位度量),参数 $\varphi$ 对应于相位(以标准化弧度为单位度量,1弧度对应于 $360^{\circ}$ )。在傅立叶分析中,我们考虑根据它们的功率(平均能量)进行标准化后的原型振荡,标准化可以通过设定 $A=\sqrt{2}$ 来做到。因此,对于每个频率参数 $\omega$ 和相位参数 $\varphi$ ,我们得到一个正弦函数 $\textbf{cos}_{\omega, \varphi}(t):\mathbb{R}\rightarrow\mathbb{R}$ ,由下式给出
$$
\textbf{cos}_{\omega, \varphi}(t):=\sqrt{2} \cos (2 \pi(\omega t-\varphi)) \tag{2.2}
$$
对任意 $t\in\mathbb{R}$ 。因为余弦函数是周期性的,所以 $\forall k\in \mathbb{Z}$ ,将相位参数 $\varphi$ 和 $\varphi+k$ 带入上式中会得到相同的正弦函数。因此,对于相位参数只需要考虑 $\varphi\in[0,1)$ 的情况。
正弦函数泛指sin和cos函数,因为cos函数可以通过平移得到sin函数
当测量给定声音信号与频率为 $\omega$ 的正弦波的吻合程度时,我们可以自由地在时间轴上移动正弦波。该自由度由相位参数 $\varphi$ 表示。如图2.2所示,声音信号与固定频率正弦波之间的相似度主要取决于相位。如图2.1所示,在计算系数 $d_{\omega}$ 时,我们对相位做了什么?引言中概述的程序只是故事的一半。当将我们将声音信号 $f$ 与相位为 $\varphi$ 的正弦函数 $\textbf{cos}_{\omega, \varphi}(t)$ 进行比较时,我们隐含地使用了能使得计算出的相似性最大的那个相位 $\varphi$ 。为了更好地理解这一点,我们首先需要解释如何实际地去比较信号和正弦曲线,或者更一般地说,如何比较两个给定函数。
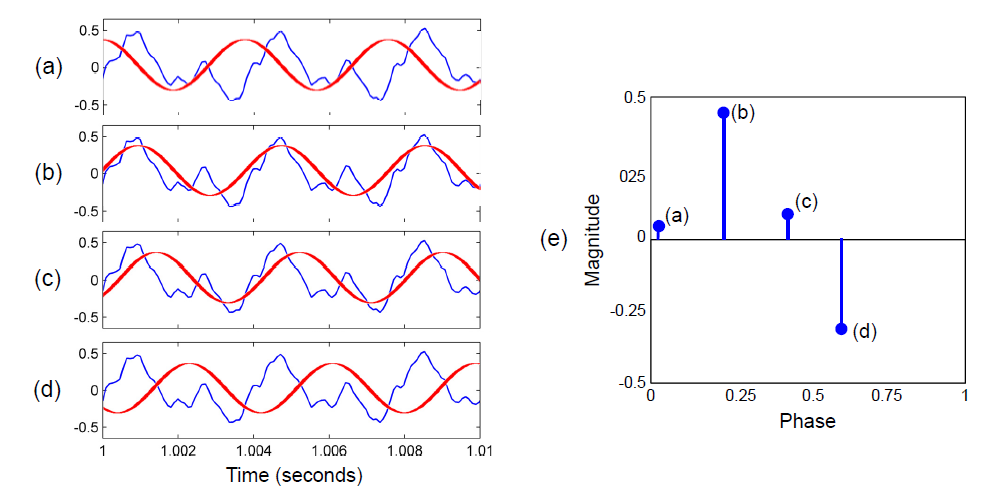 |
| 图2.2(a–d)波形本身、及其和固定频率为$\omega=262Hz$但不同相位$\varphi\in{0.05,0.24,0.45,0.6}$的不同正弦波的对比。(e)波形和四个不同正弦波之间相似程度的值。 |
稍微解释一下。以图2.1为例,我们看(c)这张图,蓝色的就是我们的声音信号,红色的是要和他进行比较的正弦函数(或者叫原型振荡),而(f)这张图中最高的那个峰值就是(c)中那两个函数之间相似性的一个刻画(把两个函数映射到一个非负实数)。还是(c)这张图,现在我们想象一下,把红色的正弦函数向右平移一小段距离,再去计算这个相似性,得到一个非负实数,这个非负实数还能比(f)图中那个原来的(c)所对应的峰值更大吗?应该是不行了,虽然不能严格说明,但从(c)图可以看到,原来红色曲线的位置已经与蓝线贴合的比较好了,如果你再把红色曲线向右平移一定,那么贴合程度势必会降低。因此,下面讨论的问题就是如何将红色曲线平移到一个合适的位置(也就是合适的相位),使得红色曲线能最好的贴合蓝色曲线。另外注意,找到这个合适的位置,计算出那个相似度,就是该频率的幅值系数$d_{\omega}$,不同频率都能计算出一个幅值系数,这就是图2.1(f)的由来。具体的数学表述见式2.4和式2.5。
假设我们有两个关于时间$t$函数 $f:\mathbb{R}\rightarrow\mathbb{R}$ 和 $g:\mathbb{R}\rightarrow\mathbb{R}$ 。$f$和$g$相似意味着什么?直观地说,如果$f$和$g$在一段时间内表现出相似的行为,人们可能会认同$f$和$g$是相似的:在$t$时刻,如果$f(t)$为正值,那么$g(t)$也应该如此,如果$f(t)$变为负值,那么$g(t)$也应该如此。通过计算两个函数乘积的积分,可以捕捉到这些函数间的共同行为:
$$
\int_{t\in\mathbb{R}}f(t)\cdot g(t)dt. \tag{2.3}
$$
这个积分测量了由$f\cdot g$的图像围出的面积,其中负面积(水平轴下方)需要从正面积(水平轴上方)中减去(见图2.3)。如果$f$和$g$在大多数情况下均为正或均为负,则乘积在大多数情况下为正,且积分变大(见图2.3a)。但是,如果两个函数不同,则整体正区域和整体负区域相互抵消,产生一个小的整体积分(见图2.3b)。练习2.1中讨论了更多示例。
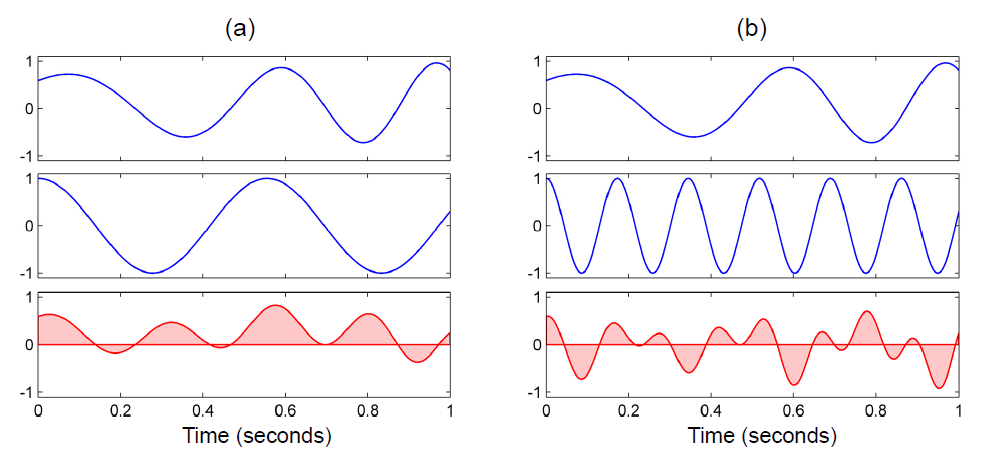 |
| 通过计算乘积的积分来计算$f$和$g$的相似性。(a)具有高度相似性的两个函数。(b)具有较低相似性的两个函数。 |
说的比较拗口,其实就是积分的几何意义。积分值越大说明两个函数相关性较高,越小说明两个函数负相关性较高(或者说$f$和$-g$相关性较高),如果接近0说明没有相关性。
以上都是数学上不严格的,只是给你一种直观感觉。
比较两个给定信号的方法还有很多。例如,函数之差的绝对值的积分也会得到一个信号间相似性的度量方法。然而,在傅里叶变换的公式中,我们遇到了类似式2.3中考虑的度量方法,涉及到线性代数中的内积的概念(见式2.37)。我们将在第2.2.3节中继续讨论。
基于相似性度量(式2.3),我们将原始信号$f$与正弦函数 $g=\textbf{cos}_{\omega, \varphi}(t)$ 进行比较,如式2.2所定义。对于某个固定频率 $\omega\in\mathbb{R}$ ,我们定义
$$
d_{\omega}:=\max {\varphi \in[0,1)}\left(\int{t \in \mathbb{R}} f(t) \textbf{cos}_{\omega, \varphi}(t) d t\right), \tag{2.4}
$$
$$
\varphi_{\omega}:=\underset{\varphi \in[0,1)}{\operatorname{argmax}}\left(\int_{t \in \mathbb{R}} f(t) \textbf{cos}_{\omega, \varphi}(t) d t\right) . \tag{2.5}
$$
如前所述,幅度系数 $d_{\omega}$ 表示信号 $f$ 内频率 $\omega$ 的强度。此外,相位系数 $\varphi_{\omega}\in[0,1)$ 告诉我们频率为 $\omega$ 的正弦波需要如何在时间上位移以最佳地拟合信号 $f$ 。函数 $f:\mathbb{R}\rightarrow\mathbb{R}$ 的傅里叶变换被定义为对所有频率 $\omega\in\mathbb{R}$ 计算出的系数 $d_{\omega}$ 和 $\varphi_{\omega}$ 构成的“集合”。很快,我们将以更正式的方式叙述此定义。
$d_{\omega}$ 和 $\varphi_{\omega}$的计算感觉有点笨拙,因为它涉及到一个优化步骤。好消息是,这个优化问题有一个简单的解决方案,这是由于存在与某些正弦函数的相位和振幅相关的某些三角恒等式。使用复数的概念,这些三角恒等式将变得简单,并可以导出傅里叶变换的优雅公式。我们将在第2.3节中更详细地讨论这些问题。在下面,我们将不给出任何证明地介绍傅里叶变换公式的标准复数形式。


