diff --git a/docs/example_neohooke-LSDYNA.md b/docs/example_neohooke-LSDYNA.md
new file mode 100644
index 0000000..4255f50
--- /dev/null
+++ b/docs/example_neohooke-LSDYNA.md
@@ -0,0 +1,282 @@
+## Example: Neo-Hookean Material (in LS-DYNA)
+
+The following example discusses the implementation of the standard Neo-Hookean material model to show the usage of the tensor toolbox in LS-DYNA. The material model describes hyperelasticity and is formulated in the spatial (eulerian) configuration for 3D and axisymmetric computations (@todo not yet adapted for 2D). Be aware that in LS-Dyna umat (stress and history update) and utan (tangent) are split up, as noted in the section "User-defined tangent routine "utan"".
+
+## Kinematics
+In LS-DYNA we first have to set the option "IHYPER=1" in the material card keyword (e.g. *MAT_USER_DEFINED_MATERIAL_MODELS) to be able to access the deformation gradient  (see section "Example material card"). The latter is then stored on top of the defined number of history variables. So, in case we don't require any history variables for our material model (NHV=0), as for this hyperelastic model, the deformation gradient is stored in the initial "hsv" entries 1 to 9 columnwise. As a consquence, we can extract it via the function
+```fortran
+type(Tensor2) :: defoGrad_F
+defoGrad_F = defoGrad(hsv(1:9))
+```
+which takes the list entries 1 to 9 and stores them into the second order tensor `defoGrad_F`.
+
+## Equations
+The Cauchy stress tensor
(see section "Example material card"). The latter is then stored on top of the defined number of history variables. So, in case we don't require any history variables for our material model (NHV=0), as for this hyperelastic model, the deformation gradient is stored in the initial "hsv" entries 1 to 9 columnwise. As a consquence, we can extract it via the function
+```fortran
+type(Tensor2) :: defoGrad_F
+defoGrad_F = defoGrad(hsv(1:9))
+```
+which takes the list entries 1 to 9 and stores them into the second order tensor `defoGrad_F`.
+
+## Equations
+The Cauchy stress tensor  for the Neo-Hookean material can be computed from
+
+
for the Neo-Hookean material can be computed from
+
+![\boldsymbol{\sigma} = \frac{1}{J} \cdot \left [ \mu \cdot \left [ \boldsymbol{F} \boldsymbol{F}^T - \boldsymbol{I} \right ] + \lambda \ln(J) \boldsymbol{I} \right ]](https://latex.codecogs.com/gif.latex?\boldsymbol{\sigma}&space;=&space;\frac{1}{J}&space;\cdot&space;\left&space;[&space;\mu&space;\cdot&space;\left&space;[&space;\boldsymbol{F}&space;\boldsymbol{F}^T&space;-&space;\boldsymbol{I}&space;\right&space;]&space;+&space;\lambda&space;\ln(J)&space;\boldsymbol{I}&space;\right&space;]) +
+The Eulerian tangent modulus is computed as
+
+
+
+The Eulerian tangent modulus is computed as
+
+![\boldsymbol{E} = \frac{1}{J} \cdot \left [ \lambda \boldsymbol{I} \otimes \boldsymbol{I} + 2 \left [ \mu - \lambda \ln (J) \right ] \overset{4}{I} \right ]](https://latex.codecogs.com/gif.latex?\boldsymbol{E}&space;=&space;\frac{1}{J}&space;\cdot&space;\left&space;[&space;\lambda&space;\boldsymbol{I}&space;\otimes&space;\boldsymbol{I}&space;+&space;2&space;\left&space;[&space;\mu&space;-&space;\lambda&space;\ln&space;(J)&space;\right&space;]&space;\overset{4}{I}&space;\right&space;]) +
+With
+* Jacobian, determinant of the deformation gradient
+
+
+
+With
+* Jacobian, determinant of the deformation gradient
+
+) +* First and second Lame parameters
+
+* First and second Lame parameters
+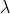 and
and 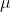 +* Second order unit/identity tensor
+
+* Second order unit/identity tensor
+ +* Fourth order unit/identity tensor
+
+* Fourth order unit/identity tensor
+ +
+## User-defined material routine "umat"
+### The commented program
+In LS-Dyna we can expand the existing file `dyn21umats.F`. At the beginning of the Fortran file include the tensor toolbox after defining the flag `NOR4`. The latter ensures that the r4 variants of implemented functions are skipped, which would else generate compiler errors in LS-Dyna (see https://github.com/adtzlr/ttb/issues/10).
+```fortran
+#define NOR4
+#include 'ttb/ttb_library.F'
+```
+Then scroll down to an unused user-defined material, for instance umat43, reading
+```fortran
+ subroutine umat43 (cm,eps,sig,epsp,hsv,dt1,capa,etype,tt,
+ 1 temper,failel,crv,nnpcrv,cma,qmat,elsiz,idele,reject)
+```
+Firstly, we have to declare the usage of the tensor module and the LS-DYNA extension.
+```fortran
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+```
+Next, the standard LS-Dyna declarations follow and don't need to be altered.
+```fortran
+c Standard LS-Dyna declarations
+ include 'nlqparm'
+ include 'bk06.inc'
+ include 'iounits.inc'
+ real(kind=8), dimension(*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*),qmat(3,3)
+ logical failel,reject
+ integer nnpcrv(*)
+ character*5 etype
+ INTEGER8 idele
+```
+Now we declare our variables.
+```fortran
+c declaration
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! Cauchy stress tensor; unit tensor
+ type(Tensor2) :: cauchyStress_sig, Eye
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+```
+Extract the material parameters from the 'cm'-array
+```fortran
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+```
+Compute the Lame parameters lambda and mu (or G)
+```fortran
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ( (1.+Poisson_nu)*(1.-2.*Poisson_nu) )
+ shearMod_mu = .5 * YoungsMod_E / (1.+Poisson_nu)
+```
+Get the unit tensor via the tensor toolbox
+```fortran
+ Eye = identity2(Eye)
+```
+Extract the deformation gradient from the history 'hsv' and transform it into the unsymmetric second order tensor as described above via the function 'defoGrad(*)' from the module TensorXLSDYNA
+```fortran
+ defoGrad_F = defoGrad( hsv(1:9) )
+```
+Compute the Jacobian as the determinant of the deformation gradient
+```fortran
+ det_F = det(defoGrad_F)
+```
+Compute the Cauchy stress for the Neo-Hookean material
+```fortran
+ cauchyStress_sig = 1./det_F * (
+ & shearMod_mu * ( (defoGrad_F * transpose(defoGrad_F)) - Eye )
+ & + lame_lambda * log(det_F) * Eye )
+```
+Transform the stress tensor into the 'sig' array
+```fortran
+ sig(1:6) = asarray(voigt(cauchyStress_sig),6)
+c
+ return
+ end
+```
+
+### The plain program
+```fortran
+ subroutine umat43 (cm,eps,sig,epsp,hsv,dt1,capa,etype,tt,
+ 1 temper,failel,crv,nnpcrv,cma,qmat,elsiz,idele,reject)
+c
+ use Tensor
+ use TensorXLSDYNA
+c
+ include 'nlqparm'
+ include 'bk06.inc'
+ include 'iounits.inc'
+ real(kind=8), dimension(*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*),qmat(3,3)
+ logical failel,reject
+ integer nnpcrv(*)
+ character*5 etype
+ INTEGER8 idele
+c
+ type(Tensor2) :: defoGrad_F
+ double precision :: det_F
+ type(Tensor2) :: cauchyStress_sig, Eye
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ( (1.+Poisson_nu)*(1.-2.*Poisson_nu) )
+ shearMod_mu = .5 * YoungsMod_E / (1.+Poisson_nu)
+c
+ Eye = identity2(Eye)
+c
+ defoGrad_F = defoGrad( hsv(1:9) )
+c
+ det_F = det(defoGrad_F)
+c
+ cauchyStress_sig = 1./det_F * (
+ & shearMod_mu * ( (defoGrad_F * transpose(defoGrad_F)) - Eye )
+ & + lame_lambda * log(det_F) * Eye )
+c
+ sig(1:6) = asarray(voigt(cauchyStress_sig),6)
+c
+ return
+ end
+```
+
+## User-defined tangent routine "utan"
+### The commented program
+In LS-Dyna the computation of the material (stress and history update) and the tangent are split up into two separate subroutines. The tangent is implemented in the file `dyn21utan.F` into the subroutines `utanXX`, where the material id `XX` has to correspond to the id of the `umatXX` subroutine it belongs to.
+We have already included the necessary files in the `dyn21umats.F` file, so for the tangent we can directly scroll down to the subroutine `utan43`.
+```fortran
+ subroutine utan43(cm,eps,sig,epsp,hsv,dt1,unsym,capa,etype,tt,
+ 1 temper,es,crv,nnpcrv,failel,cma,qmat)
+```
+We again load the modules
+```fortran
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+```
+Use the standard LS-Dyna declarations
+```fortran
+c Standard LS-Dyna declarations
+ include 'nlqparm'
+ real(kind=8), dimension (*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*)
+ integer nnpcrv(*)
+ dimension es(6,*),qmat(3,3)
+ logical failel,unsym
+ character*5 etype
+```
+Declare our variables now also containing the fourth order tensor `tangent_E` for our tangent modulus.
+```fortran
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! unit tensor
+ type(Tensor2) :: Eye
+ ! Fourth order Eulerian tangent modulus
+ type(Tensor4) :: tangent_E
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+```
+As in the umat subroutine:
+```fortran
+c Extract the material parameters from the 'cm'-array
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c Compute the Lame parameters lambda and mu (or G)
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ((1.+Poisson_nu)*(1.-2.*Poisson_nu))
+ shearMod_mu = .5*YoungsMod_E / (1.+Poisson_nu)
+c Get the unit tensor via the tensor toolbox
+ Eye = identity2(Eye)
+c Extract the deformation gradient from the history 'hsv'
+ defoGrad_F = defoGrad( hsv(1:9) )
+c Compute the Jacobian as the determinant of the deformation gradient
+ det_F = det(defoGrad_F)
+```
+In order to finally compute the Eulerian tangent for the Neo-Hookean material
+```fortran
+ tangent_E = 1./det_F * (
+ & lame_lambda * (Eye.dya.Eye) ! Be aware of the required parentheses,
+ ! Else error "An arithmetic or LOGICAL type is required in this context."
+ & + ( 2. * ( shearMod_mu - lame_lambda * log(det_F) )
+ & * identity4(Eye) )
+ & )
+```
+Eventually, we pack the fourth order tensor into the 6x6 matrix `es`
+
+```fortran
+ es(1:6,1:6) = asarray(voigt(tangent_E),6,6)
+c
+ return
+ end
+```
+and end the subroutine.
+
+### The plain program
+```fortran
+ subroutine utan43(cm,eps,sig,epsp,hsv,dt1,unsym,capa,etype,tt,
+ 1 temper,es,crv,nnpcrv,failel,cma,qmat)
+c
+ use Tensor
+ use TensorXLSDYNA
+c
+ include 'nlqparm'
+ real(kind=8), dimension (*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*)
+ integer nnpcrv(*)
+ dimension es(6,*),qmat(3,3)
+ logical failel,unsym
+ character*5 etype
+c
+ type(Tensor2) :: defoGrad_F
+ double precision :: det_F
+ type(Tensor2) :: Eye
+ type(Tensor4) :: tangent_E
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ((1.+Poisson_nu)*(1.-2.*Poisson_nu))
+ shearMod_mu = .5*YoungsMod_E / (1.+Poisson_nu)
+c
+ Eye = identity2(Eye)
+c
+ defoGrad_F = defoGrad( hsv(1:9) )
+c
+ det_F = det(defoGrad_F)
+c
+ tangent_E = 1./det_F * (
+ & lame_lambda * (Eye.dya.Eye)
+ & + ( 2. * ( shearMod_mu - lame_lambda * log(det_F) )
+ & * identity4(Eye) )
+ & )
+c
+ es(1:6,1:6) = asarray(voigt(tangent_E),6,6)
+c
+ return
+ end
+```
+
+## Example material card
+The material id in the option "MT" must equal the id in `umatXX` and `utanXX`. The value of "NHV" sets the number of used history variables, here none are used in the material model. The option "IHYPER=1" stores the deformation gradient in the history "hsv" on top of the defined "NHV". The paramters "P1" and "P2" contain the Young's modulus in "cm(1)" and the Poisson ratio in "cm(2)", respectively.
+
+
+
+## User-defined material routine "umat"
+### The commented program
+In LS-Dyna we can expand the existing file `dyn21umats.F`. At the beginning of the Fortran file include the tensor toolbox after defining the flag `NOR4`. The latter ensures that the r4 variants of implemented functions are skipped, which would else generate compiler errors in LS-Dyna (see https://github.com/adtzlr/ttb/issues/10).
+```fortran
+#define NOR4
+#include 'ttb/ttb_library.F'
+```
+Then scroll down to an unused user-defined material, for instance umat43, reading
+```fortran
+ subroutine umat43 (cm,eps,sig,epsp,hsv,dt1,capa,etype,tt,
+ 1 temper,failel,crv,nnpcrv,cma,qmat,elsiz,idele,reject)
+```
+Firstly, we have to declare the usage of the tensor module and the LS-DYNA extension.
+```fortran
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+```
+Next, the standard LS-Dyna declarations follow and don't need to be altered.
+```fortran
+c Standard LS-Dyna declarations
+ include 'nlqparm'
+ include 'bk06.inc'
+ include 'iounits.inc'
+ real(kind=8), dimension(*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*),qmat(3,3)
+ logical failel,reject
+ integer nnpcrv(*)
+ character*5 etype
+ INTEGER8 idele
+```
+Now we declare our variables.
+```fortran
+c declaration
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! Cauchy stress tensor; unit tensor
+ type(Tensor2) :: cauchyStress_sig, Eye
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+```
+Extract the material parameters from the 'cm'-array
+```fortran
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+```
+Compute the Lame parameters lambda and mu (or G)
+```fortran
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ( (1.+Poisson_nu)*(1.-2.*Poisson_nu) )
+ shearMod_mu = .5 * YoungsMod_E / (1.+Poisson_nu)
+```
+Get the unit tensor via the tensor toolbox
+```fortran
+ Eye = identity2(Eye)
+```
+Extract the deformation gradient from the history 'hsv' and transform it into the unsymmetric second order tensor as described above via the function 'defoGrad(*)' from the module TensorXLSDYNA
+```fortran
+ defoGrad_F = defoGrad( hsv(1:9) )
+```
+Compute the Jacobian as the determinant of the deformation gradient
+```fortran
+ det_F = det(defoGrad_F)
+```
+Compute the Cauchy stress for the Neo-Hookean material
+```fortran
+ cauchyStress_sig = 1./det_F * (
+ & shearMod_mu * ( (defoGrad_F * transpose(defoGrad_F)) - Eye )
+ & + lame_lambda * log(det_F) * Eye )
+```
+Transform the stress tensor into the 'sig' array
+```fortran
+ sig(1:6) = asarray(voigt(cauchyStress_sig),6)
+c
+ return
+ end
+```
+
+### The plain program
+```fortran
+ subroutine umat43 (cm,eps,sig,epsp,hsv,dt1,capa,etype,tt,
+ 1 temper,failel,crv,nnpcrv,cma,qmat,elsiz,idele,reject)
+c
+ use Tensor
+ use TensorXLSDYNA
+c
+ include 'nlqparm'
+ include 'bk06.inc'
+ include 'iounits.inc'
+ real(kind=8), dimension(*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*),qmat(3,3)
+ logical failel,reject
+ integer nnpcrv(*)
+ character*5 etype
+ INTEGER8 idele
+c
+ type(Tensor2) :: defoGrad_F
+ double precision :: det_F
+ type(Tensor2) :: cauchyStress_sig, Eye
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ( (1.+Poisson_nu)*(1.-2.*Poisson_nu) )
+ shearMod_mu = .5 * YoungsMod_E / (1.+Poisson_nu)
+c
+ Eye = identity2(Eye)
+c
+ defoGrad_F = defoGrad( hsv(1:9) )
+c
+ det_F = det(defoGrad_F)
+c
+ cauchyStress_sig = 1./det_F * (
+ & shearMod_mu * ( (defoGrad_F * transpose(defoGrad_F)) - Eye )
+ & + lame_lambda * log(det_F) * Eye )
+c
+ sig(1:6) = asarray(voigt(cauchyStress_sig),6)
+c
+ return
+ end
+```
+
+## User-defined tangent routine "utan"
+### The commented program
+In LS-Dyna the computation of the material (stress and history update) and the tangent are split up into two separate subroutines. The tangent is implemented in the file `dyn21utan.F` into the subroutines `utanXX`, where the material id `XX` has to correspond to the id of the `umatXX` subroutine it belongs to.
+We have already included the necessary files in the `dyn21umats.F` file, so for the tangent we can directly scroll down to the subroutine `utan43`.
+```fortran
+ subroutine utan43(cm,eps,sig,epsp,hsv,dt1,unsym,capa,etype,tt,
+ 1 temper,es,crv,nnpcrv,failel,cma,qmat)
+```
+We again load the modules
+```fortran
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+```
+Use the standard LS-Dyna declarations
+```fortran
+c Standard LS-Dyna declarations
+ include 'nlqparm'
+ real(kind=8), dimension (*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*)
+ integer nnpcrv(*)
+ dimension es(6,*),qmat(3,3)
+ logical failel,unsym
+ character*5 etype
+```
+Declare our variables now also containing the fourth order tensor `tangent_E` for our tangent modulus.
+```fortran
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! unit tensor
+ type(Tensor2) :: Eye
+ ! Fourth order Eulerian tangent modulus
+ type(Tensor4) :: tangent_E
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+```
+As in the umat subroutine:
+```fortran
+c Extract the material parameters from the 'cm'-array
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c Compute the Lame parameters lambda and mu (or G)
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ((1.+Poisson_nu)*(1.-2.*Poisson_nu))
+ shearMod_mu = .5*YoungsMod_E / (1.+Poisson_nu)
+c Get the unit tensor via the tensor toolbox
+ Eye = identity2(Eye)
+c Extract the deformation gradient from the history 'hsv'
+ defoGrad_F = defoGrad( hsv(1:9) )
+c Compute the Jacobian as the determinant of the deformation gradient
+ det_F = det(defoGrad_F)
+```
+In order to finally compute the Eulerian tangent for the Neo-Hookean material
+```fortran
+ tangent_E = 1./det_F * (
+ & lame_lambda * (Eye.dya.Eye) ! Be aware of the required parentheses,
+ ! Else error "An arithmetic or LOGICAL type is required in this context."
+ & + ( 2. * ( shearMod_mu - lame_lambda * log(det_F) )
+ & * identity4(Eye) )
+ & )
+```
+Eventually, we pack the fourth order tensor into the 6x6 matrix `es`
+
+```fortran
+ es(1:6,1:6) = asarray(voigt(tangent_E),6,6)
+c
+ return
+ end
+```
+and end the subroutine.
+
+### The plain program
+```fortran
+ subroutine utan43(cm,eps,sig,epsp,hsv,dt1,unsym,capa,etype,tt,
+ 1 temper,es,crv,nnpcrv,failel,cma,qmat)
+c
+ use Tensor
+ use TensorXLSDYNA
+c
+ include 'nlqparm'
+ real(kind=8), dimension (*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*)
+ integer nnpcrv(*)
+ dimension es(6,*),qmat(3,3)
+ logical failel,unsym
+ character*5 etype
+c
+ type(Tensor2) :: defoGrad_F
+ double precision :: det_F
+ type(Tensor2) :: Eye
+ type(Tensor4) :: tangent_E
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ((1.+Poisson_nu)*(1.-2.*Poisson_nu))
+ shearMod_mu = .5*YoungsMod_E / (1.+Poisson_nu)
+c
+ Eye = identity2(Eye)
+c
+ defoGrad_F = defoGrad( hsv(1:9) )
+c
+ det_F = det(defoGrad_F)
+c
+ tangent_E = 1./det_F * (
+ & lame_lambda * (Eye.dya.Eye)
+ & + ( 2. * ( shearMod_mu - lame_lambda * log(det_F) )
+ & * identity4(Eye) )
+ & )
+c
+ es(1:6,1:6) = asarray(voigt(tangent_E),6,6)
+c
+ return
+ end
+```
+
+## Example material card
+The material id in the option "MT" must equal the id in `umatXX` and `utanXX`. The value of "NHV" sets the number of used history variables, here none are used in the material model. The option "IHYPER=1" stores the deformation gradient in the history "hsv" on top of the defined "NHV". The paramters "P1" and "P2" contain the Young's modulus in "cm(1)" and the Poisson ratio in "cm(2)", respectively.
+
+ \ No newline at end of file
diff --git a/docs/examples/LSDYNA_nh_umat.F b/docs/examples/LSDYNA_nh_umat.F
new file mode 100644
index 0000000..0c4b0b4
--- /dev/null
+++ b/docs/examples/LSDYNA_nh_umat.F
@@ -0,0 +1,49 @@
+ subroutine umat47 (cm,eps,sig,epsp,hsv,dt1,capa,etype,tt,
+ 1 temper,failel,crv,nnpcrv,cma,qmat,elsiz,idele,reject)
+c
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+c Standard LS-Dyna declarations (added some explicit data types)
+ include 'nlqparm'
+ include 'bk06.inc'
+ include 'iounits.inc'
+ real(kind=8), dimension(*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*),qmat(3,3)
+ logical failel,reject
+ integer nnpcrv(*)
+ character*5 etype
+ INTEGER8 idele
+c declaration
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! Cauchy stress tensor; unit tensor
+ type(Tensor2) :: cauchyStress_sig, Eye
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c Extract the material parameters from the 'cm'-array
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c Compute the Lame parameters lambda and mu (or G)
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ( (1.+Poisson_nu)*(1.-2.*Poisson_nu) )
+ shearMod_mu = .5 * YoungsMod_E / (1.+Poisson_nu)
+c Get the unit tensor via the tensor toolbox
+ Eye = identity2(Eye)
+c Extract the deformation gradient from the history 'hsv'
+c and transform it into the unsymmetric second order tensor
+c 'defoGrad_F' via the function 'defoGrad(*)' from the module TensorXLSDYNA
+ defoGrad_F = defoGrad( hsv(1:9) )
+c Compute the Jacobian as the determinant of the deformation gradient
+ det_F = det(defoGrad_F)
+c Compute the Cauchy stress for the Neo-Hookean material
+ cauchyStress_sig = 1./det_F * (
+ & shearMod_mu * ( (defoGrad_F * transpose(defoGrad_F)) - Eye )
+ & + lame_lambda * log(det_F) * Eye )
+c Transform the stress tensor into the 'sig' array
+ sig(1:6) = asarray(voigt(cauchyStress_sig),6)
+c
+ return
+ end
\ No newline at end of file
diff --git a/docs/examples/LSDYNA_nh_utan.F b/docs/examples/LSDYNA_nh_utan.F
new file mode 100644
index 0000000..b211450
--- /dev/null
+++ b/docs/examples/LSDYNA_nh_utan.F
@@ -0,0 +1,50 @@
+ subroutine utan47(cm,eps,sig,epsp,hsv,dt1,unsym,capa,etype,tt,
+ 1 temper,es,crv,nnpcrv,failel,cma,qmat)
+c
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+c Standard LS-Dyna declarations
+ include 'nlqparm'
+ real(kind=8), dimension (*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*)
+ integer nnpcrv(*)
+ dimension es(6,*),qmat(3,3)
+ logical failel,unsym
+ character*5 etype
+c declaration
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! unit tensor
+ type(Tensor2) :: Eye
+ ! Fourth order Eulerian tangent modulus
+ type(Tensor4) :: tangent_E
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c Extract the material parameters from the 'cm'-array
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c Compute the Lame parameters lambda and mu (or G)
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ((1.+Poisson_nu)*(1.-2.*Poisson_nu))
+ shearMod_mu = .5*YoungsMod_E / (1.+Poisson_nu)
+c Get the unit tensor via the tensor toolbox
+ Eye = identity2(Eye)
+c Extract the deformation gradient from the history 'hsv'
+ defoGrad_F = defoGrad( hsv(1:9) )
+c Compute the Jacobian as the determinant of the deformation gradient
+ det_F = det(defoGrad_F)
+c Compute the Eulerian tangent for the Neo-Hookean material
+ tangent_E = 1./det_F * (
+ & lame_lambda * (Eye.dya.Eye) ! Be aware of the required parentheses,
+ ! Else error "An arithmetic or LOGICAL type is required in this context."
+ & + ( 2. * ( shearMod_mu - lame_lambda * log(det_F) )
+ & * identity4(Eye) )
+ & )
+c Transform the fourth order tensor into the 'es' matrix
+ es(1:6,1:6) = asarray(voigt(tangent_E),6,6)
+c
+ return
+ end
\ No newline at end of file
diff --git a/docs/images/LSDYNA - material-card example.png b/docs/images/LSDYNA - material-card example.png
new file mode 100644
index 0000000..f1dd928
Binary files /dev/null and b/docs/images/LSDYNA - material-card example.png differ
diff --git a/ttbXLSDYNA/libX_to_ten.f b/ttbXLSDYNA/libX_to_ten.f
new file mode 100644
index 0000000..f7c4609
--- /dev/null
+++ b/ttbXLSDYNA/libX_to_ten.f
@@ -0,0 +1,37 @@
+c Retrieve the stress tensor from the vectorization
+ function sigX_to_ten_2(sig1_i, sig2_i, sig3_i,
+ & sig4_i, sig5_i, sig6_i)
+ implicit none
+
+ type(Tensor2) :: sigX_to_ten_2
+ real sig1_i, sig2_i, sig3_i, sig4_i, sig5_i, sig6_i
+ real sig(6)
+
+ sig(1)=sig1_i
+ sig(2)=sig2_i
+ sig(3)=sig3_i
+ sig(4)=sig4_i
+ sig(5)=sig5_i
+ sig(6)=sig6_i
+ sigX_to_ten_2 = symstore_2sa(sig)
+
+ end function sigX_to_ten_2
+
+c Retrieve the strain tensor from the vectorization
+ function dX_to_ten_2(d1_i, d2_i, d3_i,
+ & d4_i, d5_i, d6_i)
+ implicit none
+
+ type(Tensor2) :: dX_to_ten_2
+ real d1_i, d2_i, d3_i, d4_i, d5_i, d6_i
+ real eps(6)
+
+ eps(1)=d1_i
+ eps(2)=d2_i
+ eps(3)=d3_i
+ eps(4)=d4_i
+ eps(5)=d5_i
+ eps(6)=d6_i
+ dX_to_ten_2 = str2ten_2s(eps,3,3,6)
+
+ end function dX_to_ten_2
\ No newline at end of file
diff --git a/ttbXLSDYNA/libdefoGrad.f b/ttbXLSDYNA/libdefoGrad.f
new file mode 100644
index 0000000..4b944cb
--- /dev/null
+++ b/ttbXLSDYNA/libdefoGrad.f
@@ -0,0 +1,39 @@
+c LSTC stores the deformation gradient in a vector, but with
+c indices running as noted below (LS-Dyna User manual Appendix-A "Deformation gradient")
+ function vec9_LSTC_to_unsymTensor_2(vec9)
+ implicit none
+
+ real(kind=8), dimension(6), intent(in) :: vec9
+ type(Tensor2) :: vec9_LSTC_to_unsymTensor_2
+
+ vec9_LSTC_to_unsymTensor_2%ab(1,1) = vec9(1)
+ vec9_LSTC_to_unsymTensor_2%ab(2,1) = vec9(2)
+ vec9_LSTC_to_unsymTensor_2%ab(3,1) = vec9(3)
+ vec9_LSTC_to_unsymTensor_2%ab(1,2) = vec9(4)
+ vec9_LSTC_to_unsymTensor_2%ab(2,2) = vec9(5)
+ vec9_LSTC_to_unsymTensor_2%ab(3,2) = vec9(6)
+ vec9_LSTC_to_unsymTensor_2%ab(1,3) = vec9(7)
+ vec9_LSTC_to_unsymTensor_2%ab(2,3) = vec9(8)
+ vec9_LSTC_to_unsymTensor_2%ab(3,3) = vec9(9)
+
+ end function vec9_LSTC_to_unsymTensor_2
+
+c The inverse function to store an unsymmetric second order tensor as the LSTC-type
+c list. (Only for the sake of completeness, usually not needed.)
+ function unsymTensor_2_to_vec9_LSTC(unsymTen2)
+ implicit none
+
+ real(kind=8), dimension(6) :: unsymTensor_2_to_vec9_LSTC
+ type(Tensor2), intent(in) :: unsymTen2
+
+ unsymTensor_2_to_vec9_LSTC(1) = unsymTen2%ab(1,1)
+ unsymTensor_2_to_vec9_LSTC(2) = unsymTen2%ab(2,1)
+ unsymTensor_2_to_vec9_LSTC(3) = unsymTen2%ab(3,1)
+ unsymTensor_2_to_vec9_LSTC(4) = unsymTen2%ab(1,2)
+ unsymTensor_2_to_vec9_LSTC(5) = unsymTen2%ab(2,2)
+ unsymTensor_2_to_vec9_LSTC(6) = unsymTen2%ab(3,2)
+ unsymTensor_2_to_vec9_LSTC(7) = unsymTen2%ab(1,3)
+ unsymTensor_2_to_vec9_LSTC(8) = unsymTen2%ab(2,3)
+ unsymTensor_2_to_vec9_LSTC(9) = unsymTen2%ab(3,3)
+
+ end function unsymTensor_2_to_vec9_LSTC
\ No newline at end of file
diff --git a/ttbXLSDYNA/libten_to_X.f b/ttbXLSDYNA/libten_to_X.f
new file mode 100644
index 0000000..e7ec6c6
--- /dev/null
+++ b/ttbXLSDYNA/libten_to_X.f
@@ -0,0 +1,19 @@
+c Store a second order stress tensor into components for vectorization
+ subroutine ten_2_to_sigX(ten_2, sig1_i, sig2_i, sig3_i,
+ & sig4_i, sig5_i, sig6_i)
+ implicit none
+
+ type(Tensor2), intent(in) :: ten_2
+ real sig1_i, sig2_i, sig3_i, sig4_i, sig5_i, sig6_i
+ real sig(6)
+
+ sig(1:6) = asarray(voigt(ten_2),6)
+ sig1_i=sig(1)
+ sig2_i=sig(2)
+ sig3_i=sig(3)
+ sig4_i=sig(4)
+ sig5_i=sig(5)
+ sig6_i=sig(6)
+ return
+ end
+
diff --git a/ttbXLSDYNA/libten_to_list.f b/ttbXLSDYNA/libten_to_list.f
new file mode 100644
index 0000000..d4ee006
--- /dev/null
+++ b/ttbXLSDYNA/libten_to_list.f
@@ -0,0 +1,40 @@
+c Store a fourth order tensor as a list with 36 entries
+ function ten_4_to_list_36(T)
+ !implicit none
+
+ ! @todo maybe check size of ten_4_to_list_36
+ type(Tensor4), intent(in) :: T
+ real(kind=8), dimension(36) :: ten_4_to_list_36
+ real, dimension(6,6) :: es
+ integer :: i,j
+ es(1:6,1:6) = asarray(asvoigt(T),6,6)
+
+ forall(i=1:6,j=1:6) ten_4_to_list_36(j+(i-1)*6) = es(i,j)
+
+ end function ten_4_to_list_36
+
+c Retrieve from a list with 36 entries the 6x6 matrix
+ function list_36_to_array_6x6(list)
+ !implicit none
+
+ real(kind=8), dimension(36) :: list
+ real, dimension(6,6) :: list_36_to_array_6x6
+ integer :: i,j
+
+ forall(i=1:6,j=1:6) list_36_to_array_6x6(i,j) = list(j+(i-1)*6)
+
+ end function list_36_to_array_6x6
+
+ !function list_36_to_ten_4(list)
+ ! implicit none
+ !
+ ! type(Tensor4) :: list_36_to_ten_4
+ ! real, dimension(36), intent(in) :: list
+ ! real, dimension(6,6) :: es
+ ! integer :: i,j
+ !
+ ! forall(i=1:6,j=1:6) es(i,j) = list(j+(i-1)*6)
+ !
+ ! list_36_to_ten_4 = symstore_4sa(es)
+ !
+ !end function list_36_to_ten_4
\ No newline at end of file
diff --git a/ttbXLSDYNA/ttbXLSDYNA_library.F b/ttbXLSDYNA/ttbXLSDYNA_library.F
new file mode 100644
index 0000000..28ca272
--- /dev/null
+++ b/ttbXLSDYNA/ttbXLSDYNA_library.F
@@ -0,0 +1,52 @@
+! -----------MODULE TENSORXLSDYNA-------------------------------
+ module TensorXLSDYNA
+ use Tensor
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+ ! use this module in the following form:
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+
+! ------BEGIN INTERFACE-------------------------------------
+ interface defoGrad
+ module procedure vec9_LSTC_to_unsymTensor_2
+ end interface
+
+ interface ten_to_list
+ module procedure ten_4_to_list_36
+ end interface
+
+ interface list_to_array
+ module procedure list_36_to_array_6x6
+ end interface
+
+ interface sigX_to_ten
+ module procedure sigX_to_ten_2
+ end interface
+
+ interface dX_to_ten
+ module procedure dX_to_ten_2
+ end interface
+
+ interface ten_to_sigX
+ module procedure ten_2_to_sigX
+ end interface
+! ------END INTERFACE---------------------------------------
+
+ contains
+
+! ------BEGIN FUNCTIONS-------------------------------------
+ include './libdefoGrad.f'
+! ------TENSOR for umatV SECTION----------------------------
+ include './libX_to_ten.f'
+ include './libten_to_list.f'
+! ------END FUNCTIONS---------------------------------------
+! ------BEGIN SUBROUTINES-----------------------------------
+ include './libten_to_X.f'
+! ------END SUBROUTINES-------------------------------------
+
+ end module TensorXLSDYNA
\ No newline at end of file
\ No newline at end of file
diff --git a/docs/examples/LSDYNA_nh_umat.F b/docs/examples/LSDYNA_nh_umat.F
new file mode 100644
index 0000000..0c4b0b4
--- /dev/null
+++ b/docs/examples/LSDYNA_nh_umat.F
@@ -0,0 +1,49 @@
+ subroutine umat47 (cm,eps,sig,epsp,hsv,dt1,capa,etype,tt,
+ 1 temper,failel,crv,nnpcrv,cma,qmat,elsiz,idele,reject)
+c
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+c Standard LS-Dyna declarations (added some explicit data types)
+ include 'nlqparm'
+ include 'bk06.inc'
+ include 'iounits.inc'
+ real(kind=8), dimension(*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*),qmat(3,3)
+ logical failel,reject
+ integer nnpcrv(*)
+ character*5 etype
+ INTEGER8 idele
+c declaration
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! Cauchy stress tensor; unit tensor
+ type(Tensor2) :: cauchyStress_sig, Eye
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c Extract the material parameters from the 'cm'-array
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c Compute the Lame parameters lambda and mu (or G)
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ( (1.+Poisson_nu)*(1.-2.*Poisson_nu) )
+ shearMod_mu = .5 * YoungsMod_E / (1.+Poisson_nu)
+c Get the unit tensor via the tensor toolbox
+ Eye = identity2(Eye)
+c Extract the deformation gradient from the history 'hsv'
+c and transform it into the unsymmetric second order tensor
+c 'defoGrad_F' via the function 'defoGrad(*)' from the module TensorXLSDYNA
+ defoGrad_F = defoGrad( hsv(1:9) )
+c Compute the Jacobian as the determinant of the deformation gradient
+ det_F = det(defoGrad_F)
+c Compute the Cauchy stress for the Neo-Hookean material
+ cauchyStress_sig = 1./det_F * (
+ & shearMod_mu * ( (defoGrad_F * transpose(defoGrad_F)) - Eye )
+ & + lame_lambda * log(det_F) * Eye )
+c Transform the stress tensor into the 'sig' array
+ sig(1:6) = asarray(voigt(cauchyStress_sig),6)
+c
+ return
+ end
\ No newline at end of file
diff --git a/docs/examples/LSDYNA_nh_utan.F b/docs/examples/LSDYNA_nh_utan.F
new file mode 100644
index 0000000..b211450
--- /dev/null
+++ b/docs/examples/LSDYNA_nh_utan.F
@@ -0,0 +1,50 @@
+ subroutine utan47(cm,eps,sig,epsp,hsv,dt1,unsym,capa,etype,tt,
+ 1 temper,es,crv,nnpcrv,failel,cma,qmat)
+c
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+c Standard LS-Dyna declarations
+ include 'nlqparm'
+ real(kind=8), dimension (*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*)
+ integer nnpcrv(*)
+ dimension es(6,*),qmat(3,3)
+ logical failel,unsym
+ character*5 etype
+c declaration
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! unit tensor
+ type(Tensor2) :: Eye
+ ! Fourth order Eulerian tangent modulus
+ type(Tensor4) :: tangent_E
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c Extract the material parameters from the 'cm'-array
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c Compute the Lame parameters lambda and mu (or G)
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ((1.+Poisson_nu)*(1.-2.*Poisson_nu))
+ shearMod_mu = .5*YoungsMod_E / (1.+Poisson_nu)
+c Get the unit tensor via the tensor toolbox
+ Eye = identity2(Eye)
+c Extract the deformation gradient from the history 'hsv'
+ defoGrad_F = defoGrad( hsv(1:9) )
+c Compute the Jacobian as the determinant of the deformation gradient
+ det_F = det(defoGrad_F)
+c Compute the Eulerian tangent for the Neo-Hookean material
+ tangent_E = 1./det_F * (
+ & lame_lambda * (Eye.dya.Eye) ! Be aware of the required parentheses,
+ ! Else error "An arithmetic or LOGICAL type is required in this context."
+ & + ( 2. * ( shearMod_mu - lame_lambda * log(det_F) )
+ & * identity4(Eye) )
+ & )
+c Transform the fourth order tensor into the 'es' matrix
+ es(1:6,1:6) = asarray(voigt(tangent_E),6,6)
+c
+ return
+ end
\ No newline at end of file
diff --git a/docs/images/LSDYNA - material-card example.png b/docs/images/LSDYNA - material-card example.png
new file mode 100644
index 0000000..f1dd928
Binary files /dev/null and b/docs/images/LSDYNA - material-card example.png differ
diff --git a/ttbXLSDYNA/libX_to_ten.f b/ttbXLSDYNA/libX_to_ten.f
new file mode 100644
index 0000000..f7c4609
--- /dev/null
+++ b/ttbXLSDYNA/libX_to_ten.f
@@ -0,0 +1,37 @@
+c Retrieve the stress tensor from the vectorization
+ function sigX_to_ten_2(sig1_i, sig2_i, sig3_i,
+ & sig4_i, sig5_i, sig6_i)
+ implicit none
+
+ type(Tensor2) :: sigX_to_ten_2
+ real sig1_i, sig2_i, sig3_i, sig4_i, sig5_i, sig6_i
+ real sig(6)
+
+ sig(1)=sig1_i
+ sig(2)=sig2_i
+ sig(3)=sig3_i
+ sig(4)=sig4_i
+ sig(5)=sig5_i
+ sig(6)=sig6_i
+ sigX_to_ten_2 = symstore_2sa(sig)
+
+ end function sigX_to_ten_2
+
+c Retrieve the strain tensor from the vectorization
+ function dX_to_ten_2(d1_i, d2_i, d3_i,
+ & d4_i, d5_i, d6_i)
+ implicit none
+
+ type(Tensor2) :: dX_to_ten_2
+ real d1_i, d2_i, d3_i, d4_i, d5_i, d6_i
+ real eps(6)
+
+ eps(1)=d1_i
+ eps(2)=d2_i
+ eps(3)=d3_i
+ eps(4)=d4_i
+ eps(5)=d5_i
+ eps(6)=d6_i
+ dX_to_ten_2 = str2ten_2s(eps,3,3,6)
+
+ end function dX_to_ten_2
\ No newline at end of file
diff --git a/ttbXLSDYNA/libdefoGrad.f b/ttbXLSDYNA/libdefoGrad.f
new file mode 100644
index 0000000..4b944cb
--- /dev/null
+++ b/ttbXLSDYNA/libdefoGrad.f
@@ -0,0 +1,39 @@
+c LSTC stores the deformation gradient in a vector, but with
+c indices running as noted below (LS-Dyna User manual Appendix-A "Deformation gradient")
+ function vec9_LSTC_to_unsymTensor_2(vec9)
+ implicit none
+
+ real(kind=8), dimension(6), intent(in) :: vec9
+ type(Tensor2) :: vec9_LSTC_to_unsymTensor_2
+
+ vec9_LSTC_to_unsymTensor_2%ab(1,1) = vec9(1)
+ vec9_LSTC_to_unsymTensor_2%ab(2,1) = vec9(2)
+ vec9_LSTC_to_unsymTensor_2%ab(3,1) = vec9(3)
+ vec9_LSTC_to_unsymTensor_2%ab(1,2) = vec9(4)
+ vec9_LSTC_to_unsymTensor_2%ab(2,2) = vec9(5)
+ vec9_LSTC_to_unsymTensor_2%ab(3,2) = vec9(6)
+ vec9_LSTC_to_unsymTensor_2%ab(1,3) = vec9(7)
+ vec9_LSTC_to_unsymTensor_2%ab(2,3) = vec9(8)
+ vec9_LSTC_to_unsymTensor_2%ab(3,3) = vec9(9)
+
+ end function vec9_LSTC_to_unsymTensor_2
+
+c The inverse function to store an unsymmetric second order tensor as the LSTC-type
+c list. (Only for the sake of completeness, usually not needed.)
+ function unsymTensor_2_to_vec9_LSTC(unsymTen2)
+ implicit none
+
+ real(kind=8), dimension(6) :: unsymTensor_2_to_vec9_LSTC
+ type(Tensor2), intent(in) :: unsymTen2
+
+ unsymTensor_2_to_vec9_LSTC(1) = unsymTen2%ab(1,1)
+ unsymTensor_2_to_vec9_LSTC(2) = unsymTen2%ab(2,1)
+ unsymTensor_2_to_vec9_LSTC(3) = unsymTen2%ab(3,1)
+ unsymTensor_2_to_vec9_LSTC(4) = unsymTen2%ab(1,2)
+ unsymTensor_2_to_vec9_LSTC(5) = unsymTen2%ab(2,2)
+ unsymTensor_2_to_vec9_LSTC(6) = unsymTen2%ab(3,2)
+ unsymTensor_2_to_vec9_LSTC(7) = unsymTen2%ab(1,3)
+ unsymTensor_2_to_vec9_LSTC(8) = unsymTen2%ab(2,3)
+ unsymTensor_2_to_vec9_LSTC(9) = unsymTen2%ab(3,3)
+
+ end function unsymTensor_2_to_vec9_LSTC
\ No newline at end of file
diff --git a/ttbXLSDYNA/libten_to_X.f b/ttbXLSDYNA/libten_to_X.f
new file mode 100644
index 0000000..e7ec6c6
--- /dev/null
+++ b/ttbXLSDYNA/libten_to_X.f
@@ -0,0 +1,19 @@
+c Store a second order stress tensor into components for vectorization
+ subroutine ten_2_to_sigX(ten_2, sig1_i, sig2_i, sig3_i,
+ & sig4_i, sig5_i, sig6_i)
+ implicit none
+
+ type(Tensor2), intent(in) :: ten_2
+ real sig1_i, sig2_i, sig3_i, sig4_i, sig5_i, sig6_i
+ real sig(6)
+
+ sig(1:6) = asarray(voigt(ten_2),6)
+ sig1_i=sig(1)
+ sig2_i=sig(2)
+ sig3_i=sig(3)
+ sig4_i=sig(4)
+ sig5_i=sig(5)
+ sig6_i=sig(6)
+ return
+ end
+
diff --git a/ttbXLSDYNA/libten_to_list.f b/ttbXLSDYNA/libten_to_list.f
new file mode 100644
index 0000000..d4ee006
--- /dev/null
+++ b/ttbXLSDYNA/libten_to_list.f
@@ -0,0 +1,40 @@
+c Store a fourth order tensor as a list with 36 entries
+ function ten_4_to_list_36(T)
+ !implicit none
+
+ ! @todo maybe check size of ten_4_to_list_36
+ type(Tensor4), intent(in) :: T
+ real(kind=8), dimension(36) :: ten_4_to_list_36
+ real, dimension(6,6) :: es
+ integer :: i,j
+ es(1:6,1:6) = asarray(asvoigt(T),6,6)
+
+ forall(i=1:6,j=1:6) ten_4_to_list_36(j+(i-1)*6) = es(i,j)
+
+ end function ten_4_to_list_36
+
+c Retrieve from a list with 36 entries the 6x6 matrix
+ function list_36_to_array_6x6(list)
+ !implicit none
+
+ real(kind=8), dimension(36) :: list
+ real, dimension(6,6) :: list_36_to_array_6x6
+ integer :: i,j
+
+ forall(i=1:6,j=1:6) list_36_to_array_6x6(i,j) = list(j+(i-1)*6)
+
+ end function list_36_to_array_6x6
+
+ !function list_36_to_ten_4(list)
+ ! implicit none
+ !
+ ! type(Tensor4) :: list_36_to_ten_4
+ ! real, dimension(36), intent(in) :: list
+ ! real, dimension(6,6) :: es
+ ! integer :: i,j
+ !
+ ! forall(i=1:6,j=1:6) es(i,j) = list(j+(i-1)*6)
+ !
+ ! list_36_to_ten_4 = symstore_4sa(es)
+ !
+ !end function list_36_to_ten_4
\ No newline at end of file
diff --git a/ttbXLSDYNA/ttbXLSDYNA_library.F b/ttbXLSDYNA/ttbXLSDYNA_library.F
new file mode 100644
index 0000000..28ca272
--- /dev/null
+++ b/ttbXLSDYNA/ttbXLSDYNA_library.F
@@ -0,0 +1,52 @@
+! -----------MODULE TENSORXLSDYNA-------------------------------
+ module TensorXLSDYNA
+ use Tensor
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+ ! use this module in the following form:
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+
+! ------BEGIN INTERFACE-------------------------------------
+ interface defoGrad
+ module procedure vec9_LSTC_to_unsymTensor_2
+ end interface
+
+ interface ten_to_list
+ module procedure ten_4_to_list_36
+ end interface
+
+ interface list_to_array
+ module procedure list_36_to_array_6x6
+ end interface
+
+ interface sigX_to_ten
+ module procedure sigX_to_ten_2
+ end interface
+
+ interface dX_to_ten
+ module procedure dX_to_ten_2
+ end interface
+
+ interface ten_to_sigX
+ module procedure ten_2_to_sigX
+ end interface
+! ------END INTERFACE---------------------------------------
+
+ contains
+
+! ------BEGIN FUNCTIONS-------------------------------------
+ include './libdefoGrad.f'
+! ------TENSOR for umatV SECTION----------------------------
+ include './libX_to_ten.f'
+ include './libten_to_list.f'
+! ------END FUNCTIONS---------------------------------------
+! ------BEGIN SUBROUTINES-----------------------------------
+ include './libten_to_X.f'
+! ------END SUBROUTINES-------------------------------------
+
+ end module TensorXLSDYNA
\ No newline at end of file
 \ No newline at end of file
diff --git a/docs/examples/LSDYNA_nh_umat.F b/docs/examples/LSDYNA_nh_umat.F
new file mode 100644
index 0000000..0c4b0b4
--- /dev/null
+++ b/docs/examples/LSDYNA_nh_umat.F
@@ -0,0 +1,49 @@
+ subroutine umat47 (cm,eps,sig,epsp,hsv,dt1,capa,etype,tt,
+ 1 temper,failel,crv,nnpcrv,cma,qmat,elsiz,idele,reject)
+c
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+c Standard LS-Dyna declarations (added some explicit data types)
+ include 'nlqparm'
+ include 'bk06.inc'
+ include 'iounits.inc'
+ real(kind=8), dimension(*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*),qmat(3,3)
+ logical failel,reject
+ integer nnpcrv(*)
+ character*5 etype
+ INTEGER8 idele
+c declaration
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! Cauchy stress tensor; unit tensor
+ type(Tensor2) :: cauchyStress_sig, Eye
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c Extract the material parameters from the 'cm'-array
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c Compute the Lame parameters lambda and mu (or G)
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ( (1.+Poisson_nu)*(1.-2.*Poisson_nu) )
+ shearMod_mu = .5 * YoungsMod_E / (1.+Poisson_nu)
+c Get the unit tensor via the tensor toolbox
+ Eye = identity2(Eye)
+c Extract the deformation gradient from the history 'hsv'
+c and transform it into the unsymmetric second order tensor
+c 'defoGrad_F' via the function 'defoGrad(*)' from the module TensorXLSDYNA
+ defoGrad_F = defoGrad( hsv(1:9) )
+c Compute the Jacobian as the determinant of the deformation gradient
+ det_F = det(defoGrad_F)
+c Compute the Cauchy stress for the Neo-Hookean material
+ cauchyStress_sig = 1./det_F * (
+ & shearMod_mu * ( (defoGrad_F * transpose(defoGrad_F)) - Eye )
+ & + lame_lambda * log(det_F) * Eye )
+c Transform the stress tensor into the 'sig' array
+ sig(1:6) = asarray(voigt(cauchyStress_sig),6)
+c
+ return
+ end
\ No newline at end of file
diff --git a/docs/examples/LSDYNA_nh_utan.F b/docs/examples/LSDYNA_nh_utan.F
new file mode 100644
index 0000000..b211450
--- /dev/null
+++ b/docs/examples/LSDYNA_nh_utan.F
@@ -0,0 +1,50 @@
+ subroutine utan47(cm,eps,sig,epsp,hsv,dt1,unsym,capa,etype,tt,
+ 1 temper,es,crv,nnpcrv,failel,cma,qmat)
+c
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+c Standard LS-Dyna declarations
+ include 'nlqparm'
+ real(kind=8), dimension (*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*)
+ integer nnpcrv(*)
+ dimension es(6,*),qmat(3,3)
+ logical failel,unsym
+ character*5 etype
+c declaration
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! unit tensor
+ type(Tensor2) :: Eye
+ ! Fourth order Eulerian tangent modulus
+ type(Tensor4) :: tangent_E
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c Extract the material parameters from the 'cm'-array
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c Compute the Lame parameters lambda and mu (or G)
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ((1.+Poisson_nu)*(1.-2.*Poisson_nu))
+ shearMod_mu = .5*YoungsMod_E / (1.+Poisson_nu)
+c Get the unit tensor via the tensor toolbox
+ Eye = identity2(Eye)
+c Extract the deformation gradient from the history 'hsv'
+ defoGrad_F = defoGrad( hsv(1:9) )
+c Compute the Jacobian as the determinant of the deformation gradient
+ det_F = det(defoGrad_F)
+c Compute the Eulerian tangent for the Neo-Hookean material
+ tangent_E = 1./det_F * (
+ & lame_lambda * (Eye.dya.Eye) ! Be aware of the required parentheses,
+ ! Else error "An arithmetic or LOGICAL type is required in this context."
+ & + ( 2. * ( shearMod_mu - lame_lambda * log(det_F) )
+ & * identity4(Eye) )
+ & )
+c Transform the fourth order tensor into the 'es' matrix
+ es(1:6,1:6) = asarray(voigt(tangent_E),6,6)
+c
+ return
+ end
\ No newline at end of file
diff --git a/docs/images/LSDYNA - material-card example.png b/docs/images/LSDYNA - material-card example.png
new file mode 100644
index 0000000..f1dd928
Binary files /dev/null and b/docs/images/LSDYNA - material-card example.png differ
diff --git a/ttbXLSDYNA/libX_to_ten.f b/ttbXLSDYNA/libX_to_ten.f
new file mode 100644
index 0000000..f7c4609
--- /dev/null
+++ b/ttbXLSDYNA/libX_to_ten.f
@@ -0,0 +1,37 @@
+c Retrieve the stress tensor from the vectorization
+ function sigX_to_ten_2(sig1_i, sig2_i, sig3_i,
+ & sig4_i, sig5_i, sig6_i)
+ implicit none
+
+ type(Tensor2) :: sigX_to_ten_2
+ real sig1_i, sig2_i, sig3_i, sig4_i, sig5_i, sig6_i
+ real sig(6)
+
+ sig(1)=sig1_i
+ sig(2)=sig2_i
+ sig(3)=sig3_i
+ sig(4)=sig4_i
+ sig(5)=sig5_i
+ sig(6)=sig6_i
+ sigX_to_ten_2 = symstore_2sa(sig)
+
+ end function sigX_to_ten_2
+
+c Retrieve the strain tensor from the vectorization
+ function dX_to_ten_2(d1_i, d2_i, d3_i,
+ & d4_i, d5_i, d6_i)
+ implicit none
+
+ type(Tensor2) :: dX_to_ten_2
+ real d1_i, d2_i, d3_i, d4_i, d5_i, d6_i
+ real eps(6)
+
+ eps(1)=d1_i
+ eps(2)=d2_i
+ eps(3)=d3_i
+ eps(4)=d4_i
+ eps(5)=d5_i
+ eps(6)=d6_i
+ dX_to_ten_2 = str2ten_2s(eps,3,3,6)
+
+ end function dX_to_ten_2
\ No newline at end of file
diff --git a/ttbXLSDYNA/libdefoGrad.f b/ttbXLSDYNA/libdefoGrad.f
new file mode 100644
index 0000000..4b944cb
--- /dev/null
+++ b/ttbXLSDYNA/libdefoGrad.f
@@ -0,0 +1,39 @@
+c LSTC stores the deformation gradient in a vector, but with
+c indices running as noted below (LS-Dyna User manual Appendix-A "Deformation gradient")
+ function vec9_LSTC_to_unsymTensor_2(vec9)
+ implicit none
+
+ real(kind=8), dimension(6), intent(in) :: vec9
+ type(Tensor2) :: vec9_LSTC_to_unsymTensor_2
+
+ vec9_LSTC_to_unsymTensor_2%ab(1,1) = vec9(1)
+ vec9_LSTC_to_unsymTensor_2%ab(2,1) = vec9(2)
+ vec9_LSTC_to_unsymTensor_2%ab(3,1) = vec9(3)
+ vec9_LSTC_to_unsymTensor_2%ab(1,2) = vec9(4)
+ vec9_LSTC_to_unsymTensor_2%ab(2,2) = vec9(5)
+ vec9_LSTC_to_unsymTensor_2%ab(3,2) = vec9(6)
+ vec9_LSTC_to_unsymTensor_2%ab(1,3) = vec9(7)
+ vec9_LSTC_to_unsymTensor_2%ab(2,3) = vec9(8)
+ vec9_LSTC_to_unsymTensor_2%ab(3,3) = vec9(9)
+
+ end function vec9_LSTC_to_unsymTensor_2
+
+c The inverse function to store an unsymmetric second order tensor as the LSTC-type
+c list. (Only for the sake of completeness, usually not needed.)
+ function unsymTensor_2_to_vec9_LSTC(unsymTen2)
+ implicit none
+
+ real(kind=8), dimension(6) :: unsymTensor_2_to_vec9_LSTC
+ type(Tensor2), intent(in) :: unsymTen2
+
+ unsymTensor_2_to_vec9_LSTC(1) = unsymTen2%ab(1,1)
+ unsymTensor_2_to_vec9_LSTC(2) = unsymTen2%ab(2,1)
+ unsymTensor_2_to_vec9_LSTC(3) = unsymTen2%ab(3,1)
+ unsymTensor_2_to_vec9_LSTC(4) = unsymTen2%ab(1,2)
+ unsymTensor_2_to_vec9_LSTC(5) = unsymTen2%ab(2,2)
+ unsymTensor_2_to_vec9_LSTC(6) = unsymTen2%ab(3,2)
+ unsymTensor_2_to_vec9_LSTC(7) = unsymTen2%ab(1,3)
+ unsymTensor_2_to_vec9_LSTC(8) = unsymTen2%ab(2,3)
+ unsymTensor_2_to_vec9_LSTC(9) = unsymTen2%ab(3,3)
+
+ end function unsymTensor_2_to_vec9_LSTC
\ No newline at end of file
diff --git a/ttbXLSDYNA/libten_to_X.f b/ttbXLSDYNA/libten_to_X.f
new file mode 100644
index 0000000..e7ec6c6
--- /dev/null
+++ b/ttbXLSDYNA/libten_to_X.f
@@ -0,0 +1,19 @@
+c Store a second order stress tensor into components for vectorization
+ subroutine ten_2_to_sigX(ten_2, sig1_i, sig2_i, sig3_i,
+ & sig4_i, sig5_i, sig6_i)
+ implicit none
+
+ type(Tensor2), intent(in) :: ten_2
+ real sig1_i, sig2_i, sig3_i, sig4_i, sig5_i, sig6_i
+ real sig(6)
+
+ sig(1:6) = asarray(voigt(ten_2),6)
+ sig1_i=sig(1)
+ sig2_i=sig(2)
+ sig3_i=sig(3)
+ sig4_i=sig(4)
+ sig5_i=sig(5)
+ sig6_i=sig(6)
+ return
+ end
+
diff --git a/ttbXLSDYNA/libten_to_list.f b/ttbXLSDYNA/libten_to_list.f
new file mode 100644
index 0000000..d4ee006
--- /dev/null
+++ b/ttbXLSDYNA/libten_to_list.f
@@ -0,0 +1,40 @@
+c Store a fourth order tensor as a list with 36 entries
+ function ten_4_to_list_36(T)
+ !implicit none
+
+ ! @todo maybe check size of ten_4_to_list_36
+ type(Tensor4), intent(in) :: T
+ real(kind=8), dimension(36) :: ten_4_to_list_36
+ real, dimension(6,6) :: es
+ integer :: i,j
+ es(1:6,1:6) = asarray(asvoigt(T),6,6)
+
+ forall(i=1:6,j=1:6) ten_4_to_list_36(j+(i-1)*6) = es(i,j)
+
+ end function ten_4_to_list_36
+
+c Retrieve from a list with 36 entries the 6x6 matrix
+ function list_36_to_array_6x6(list)
+ !implicit none
+
+ real(kind=8), dimension(36) :: list
+ real, dimension(6,6) :: list_36_to_array_6x6
+ integer :: i,j
+
+ forall(i=1:6,j=1:6) list_36_to_array_6x6(i,j) = list(j+(i-1)*6)
+
+ end function list_36_to_array_6x6
+
+ !function list_36_to_ten_4(list)
+ ! implicit none
+ !
+ ! type(Tensor4) :: list_36_to_ten_4
+ ! real, dimension(36), intent(in) :: list
+ ! real, dimension(6,6) :: es
+ ! integer :: i,j
+ !
+ ! forall(i=1:6,j=1:6) es(i,j) = list(j+(i-1)*6)
+ !
+ ! list_36_to_ten_4 = symstore_4sa(es)
+ !
+ !end function list_36_to_ten_4
\ No newline at end of file
diff --git a/ttbXLSDYNA/ttbXLSDYNA_library.F b/ttbXLSDYNA/ttbXLSDYNA_library.F
new file mode 100644
index 0000000..28ca272
--- /dev/null
+++ b/ttbXLSDYNA/ttbXLSDYNA_library.F
@@ -0,0 +1,52 @@
+! -----------MODULE TENSORXLSDYNA-------------------------------
+ module TensorXLSDYNA
+ use Tensor
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+ ! use this module in the following form:
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+
+! ------BEGIN INTERFACE-------------------------------------
+ interface defoGrad
+ module procedure vec9_LSTC_to_unsymTensor_2
+ end interface
+
+ interface ten_to_list
+ module procedure ten_4_to_list_36
+ end interface
+
+ interface list_to_array
+ module procedure list_36_to_array_6x6
+ end interface
+
+ interface sigX_to_ten
+ module procedure sigX_to_ten_2
+ end interface
+
+ interface dX_to_ten
+ module procedure dX_to_ten_2
+ end interface
+
+ interface ten_to_sigX
+ module procedure ten_2_to_sigX
+ end interface
+! ------END INTERFACE---------------------------------------
+
+ contains
+
+! ------BEGIN FUNCTIONS-------------------------------------
+ include './libdefoGrad.f'
+! ------TENSOR for umatV SECTION----------------------------
+ include './libX_to_ten.f'
+ include './libten_to_list.f'
+! ------END FUNCTIONS---------------------------------------
+! ------BEGIN SUBROUTINES-----------------------------------
+ include './libten_to_X.f'
+! ------END SUBROUTINES-------------------------------------
+
+ end module TensorXLSDYNA
\ No newline at end of file
\ No newline at end of file
diff --git a/docs/examples/LSDYNA_nh_umat.F b/docs/examples/LSDYNA_nh_umat.F
new file mode 100644
index 0000000..0c4b0b4
--- /dev/null
+++ b/docs/examples/LSDYNA_nh_umat.F
@@ -0,0 +1,49 @@
+ subroutine umat47 (cm,eps,sig,epsp,hsv,dt1,capa,etype,tt,
+ 1 temper,failel,crv,nnpcrv,cma,qmat,elsiz,idele,reject)
+c
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+c Standard LS-Dyna declarations (added some explicit data types)
+ include 'nlqparm'
+ include 'bk06.inc'
+ include 'iounits.inc'
+ real(kind=8), dimension(*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*),qmat(3,3)
+ logical failel,reject
+ integer nnpcrv(*)
+ character*5 etype
+ INTEGER8 idele
+c declaration
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! Cauchy stress tensor; unit tensor
+ type(Tensor2) :: cauchyStress_sig, Eye
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c Extract the material parameters from the 'cm'-array
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c Compute the Lame parameters lambda and mu (or G)
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ( (1.+Poisson_nu)*(1.-2.*Poisson_nu) )
+ shearMod_mu = .5 * YoungsMod_E / (1.+Poisson_nu)
+c Get the unit tensor via the tensor toolbox
+ Eye = identity2(Eye)
+c Extract the deformation gradient from the history 'hsv'
+c and transform it into the unsymmetric second order tensor
+c 'defoGrad_F' via the function 'defoGrad(*)' from the module TensorXLSDYNA
+ defoGrad_F = defoGrad( hsv(1:9) )
+c Compute the Jacobian as the determinant of the deformation gradient
+ det_F = det(defoGrad_F)
+c Compute the Cauchy stress for the Neo-Hookean material
+ cauchyStress_sig = 1./det_F * (
+ & shearMod_mu * ( (defoGrad_F * transpose(defoGrad_F)) - Eye )
+ & + lame_lambda * log(det_F) * Eye )
+c Transform the stress tensor into the 'sig' array
+ sig(1:6) = asarray(voigt(cauchyStress_sig),6)
+c
+ return
+ end
\ No newline at end of file
diff --git a/docs/examples/LSDYNA_nh_utan.F b/docs/examples/LSDYNA_nh_utan.F
new file mode 100644
index 0000000..b211450
--- /dev/null
+++ b/docs/examples/LSDYNA_nh_utan.F
@@ -0,0 +1,50 @@
+ subroutine utan47(cm,eps,sig,epsp,hsv,dt1,unsym,capa,etype,tt,
+ 1 temper,es,crv,nnpcrv,failel,cma,qmat)
+c
+c Use the tensor toolbox
+ use Tensor
+ use TensorXLSDYNA
+c Standard LS-Dyna declarations
+ include 'nlqparm'
+ real(kind=8), dimension (*) :: cm, eps, sig, hsv
+ dimension crv(lq1,2,*),cma(*)
+ integer nnpcrv(*)
+ dimension es(6,*),qmat(3,3)
+ logical failel,unsym
+ character*5 etype
+c declaration
+ ! Deformation gradient (unsymmetric second order tensor)
+ type(Tensor2) :: defoGrad_F
+ ! Jacobian, determinant of the deformation gradient
+ double precision :: det_F
+ ! unit tensor
+ type(Tensor2) :: Eye
+ ! Fourth order Eulerian tangent modulus
+ type(Tensor4) :: tangent_E
+ ! material parameters
+ double precision YoungsMod_E, Poisson_nu, lame_lambda, shearMod_mu
+c Extract the material parameters from the 'cm'-array
+ YoungsMod_E = cm(1)
+ Poisson_nu = cm(2)
+c Compute the Lame parameters lambda and mu (or G)
+ lame_lambda = YoungsMod_E * Poisson_nu
+ & / ((1.+Poisson_nu)*(1.-2.*Poisson_nu))
+ shearMod_mu = .5*YoungsMod_E / (1.+Poisson_nu)
+c Get the unit tensor via the tensor toolbox
+ Eye = identity2(Eye)
+c Extract the deformation gradient from the history 'hsv'
+ defoGrad_F = defoGrad( hsv(1:9) )
+c Compute the Jacobian as the determinant of the deformation gradient
+ det_F = det(defoGrad_F)
+c Compute the Eulerian tangent for the Neo-Hookean material
+ tangent_E = 1./det_F * (
+ & lame_lambda * (Eye.dya.Eye) ! Be aware of the required parentheses,
+ ! Else error "An arithmetic or LOGICAL type is required in this context."
+ & + ( 2. * ( shearMod_mu - lame_lambda * log(det_F) )
+ & * identity4(Eye) )
+ & )
+c Transform the fourth order tensor into the 'es' matrix
+ es(1:6,1:6) = asarray(voigt(tangent_E),6,6)
+c
+ return
+ end
\ No newline at end of file
diff --git a/docs/images/LSDYNA - material-card example.png b/docs/images/LSDYNA - material-card example.png
new file mode 100644
index 0000000..f1dd928
Binary files /dev/null and b/docs/images/LSDYNA - material-card example.png differ
diff --git a/ttbXLSDYNA/libX_to_ten.f b/ttbXLSDYNA/libX_to_ten.f
new file mode 100644
index 0000000..f7c4609
--- /dev/null
+++ b/ttbXLSDYNA/libX_to_ten.f
@@ -0,0 +1,37 @@
+c Retrieve the stress tensor from the vectorization
+ function sigX_to_ten_2(sig1_i, sig2_i, sig3_i,
+ & sig4_i, sig5_i, sig6_i)
+ implicit none
+
+ type(Tensor2) :: sigX_to_ten_2
+ real sig1_i, sig2_i, sig3_i, sig4_i, sig5_i, sig6_i
+ real sig(6)
+
+ sig(1)=sig1_i
+ sig(2)=sig2_i
+ sig(3)=sig3_i
+ sig(4)=sig4_i
+ sig(5)=sig5_i
+ sig(6)=sig6_i
+ sigX_to_ten_2 = symstore_2sa(sig)
+
+ end function sigX_to_ten_2
+
+c Retrieve the strain tensor from the vectorization
+ function dX_to_ten_2(d1_i, d2_i, d3_i,
+ & d4_i, d5_i, d6_i)
+ implicit none
+
+ type(Tensor2) :: dX_to_ten_2
+ real d1_i, d2_i, d3_i, d4_i, d5_i, d6_i
+ real eps(6)
+
+ eps(1)=d1_i
+ eps(2)=d2_i
+ eps(3)=d3_i
+ eps(4)=d4_i
+ eps(5)=d5_i
+ eps(6)=d6_i
+ dX_to_ten_2 = str2ten_2s(eps,3,3,6)
+
+ end function dX_to_ten_2
\ No newline at end of file
diff --git a/ttbXLSDYNA/libdefoGrad.f b/ttbXLSDYNA/libdefoGrad.f
new file mode 100644
index 0000000..4b944cb
--- /dev/null
+++ b/ttbXLSDYNA/libdefoGrad.f
@@ -0,0 +1,39 @@
+c LSTC stores the deformation gradient in a vector, but with
+c indices running as noted below (LS-Dyna User manual Appendix-A "Deformation gradient")
+ function vec9_LSTC_to_unsymTensor_2(vec9)
+ implicit none
+
+ real(kind=8), dimension(6), intent(in) :: vec9
+ type(Tensor2) :: vec9_LSTC_to_unsymTensor_2
+
+ vec9_LSTC_to_unsymTensor_2%ab(1,1) = vec9(1)
+ vec9_LSTC_to_unsymTensor_2%ab(2,1) = vec9(2)
+ vec9_LSTC_to_unsymTensor_2%ab(3,1) = vec9(3)
+ vec9_LSTC_to_unsymTensor_2%ab(1,2) = vec9(4)
+ vec9_LSTC_to_unsymTensor_2%ab(2,2) = vec9(5)
+ vec9_LSTC_to_unsymTensor_2%ab(3,2) = vec9(6)
+ vec9_LSTC_to_unsymTensor_2%ab(1,3) = vec9(7)
+ vec9_LSTC_to_unsymTensor_2%ab(2,3) = vec9(8)
+ vec9_LSTC_to_unsymTensor_2%ab(3,3) = vec9(9)
+
+ end function vec9_LSTC_to_unsymTensor_2
+
+c The inverse function to store an unsymmetric second order tensor as the LSTC-type
+c list. (Only for the sake of completeness, usually not needed.)
+ function unsymTensor_2_to_vec9_LSTC(unsymTen2)
+ implicit none
+
+ real(kind=8), dimension(6) :: unsymTensor_2_to_vec9_LSTC
+ type(Tensor2), intent(in) :: unsymTen2
+
+ unsymTensor_2_to_vec9_LSTC(1) = unsymTen2%ab(1,1)
+ unsymTensor_2_to_vec9_LSTC(2) = unsymTen2%ab(2,1)
+ unsymTensor_2_to_vec9_LSTC(3) = unsymTen2%ab(3,1)
+ unsymTensor_2_to_vec9_LSTC(4) = unsymTen2%ab(1,2)
+ unsymTensor_2_to_vec9_LSTC(5) = unsymTen2%ab(2,2)
+ unsymTensor_2_to_vec9_LSTC(6) = unsymTen2%ab(3,2)
+ unsymTensor_2_to_vec9_LSTC(7) = unsymTen2%ab(1,3)
+ unsymTensor_2_to_vec9_LSTC(8) = unsymTen2%ab(2,3)
+ unsymTensor_2_to_vec9_LSTC(9) = unsymTen2%ab(3,3)
+
+ end function unsymTensor_2_to_vec9_LSTC
\ No newline at end of file
diff --git a/ttbXLSDYNA/libten_to_X.f b/ttbXLSDYNA/libten_to_X.f
new file mode 100644
index 0000000..e7ec6c6
--- /dev/null
+++ b/ttbXLSDYNA/libten_to_X.f
@@ -0,0 +1,19 @@
+c Store a second order stress tensor into components for vectorization
+ subroutine ten_2_to_sigX(ten_2, sig1_i, sig2_i, sig3_i,
+ & sig4_i, sig5_i, sig6_i)
+ implicit none
+
+ type(Tensor2), intent(in) :: ten_2
+ real sig1_i, sig2_i, sig3_i, sig4_i, sig5_i, sig6_i
+ real sig(6)
+
+ sig(1:6) = asarray(voigt(ten_2),6)
+ sig1_i=sig(1)
+ sig2_i=sig(2)
+ sig3_i=sig(3)
+ sig4_i=sig(4)
+ sig5_i=sig(5)
+ sig6_i=sig(6)
+ return
+ end
+
diff --git a/ttbXLSDYNA/libten_to_list.f b/ttbXLSDYNA/libten_to_list.f
new file mode 100644
index 0000000..d4ee006
--- /dev/null
+++ b/ttbXLSDYNA/libten_to_list.f
@@ -0,0 +1,40 @@
+c Store a fourth order tensor as a list with 36 entries
+ function ten_4_to_list_36(T)
+ !implicit none
+
+ ! @todo maybe check size of ten_4_to_list_36
+ type(Tensor4), intent(in) :: T
+ real(kind=8), dimension(36) :: ten_4_to_list_36
+ real, dimension(6,6) :: es
+ integer :: i,j
+ es(1:6,1:6) = asarray(asvoigt(T),6,6)
+
+ forall(i=1:6,j=1:6) ten_4_to_list_36(j+(i-1)*6) = es(i,j)
+
+ end function ten_4_to_list_36
+
+c Retrieve from a list with 36 entries the 6x6 matrix
+ function list_36_to_array_6x6(list)
+ !implicit none
+
+ real(kind=8), dimension(36) :: list
+ real, dimension(6,6) :: list_36_to_array_6x6
+ integer :: i,j
+
+ forall(i=1:6,j=1:6) list_36_to_array_6x6(i,j) = list(j+(i-1)*6)
+
+ end function list_36_to_array_6x6
+
+ !function list_36_to_ten_4(list)
+ ! implicit none
+ !
+ ! type(Tensor4) :: list_36_to_ten_4
+ ! real, dimension(36), intent(in) :: list
+ ! real, dimension(6,6) :: es
+ ! integer :: i,j
+ !
+ ! forall(i=1:6,j=1:6) es(i,j) = list(j+(i-1)*6)
+ !
+ ! list_36_to_ten_4 = symstore_4sa(es)
+ !
+ !end function list_36_to_ten_4
\ No newline at end of file
diff --git a/ttbXLSDYNA/ttbXLSDYNA_library.F b/ttbXLSDYNA/ttbXLSDYNA_library.F
new file mode 100644
index 0000000..28ca272
--- /dev/null
+++ b/ttbXLSDYNA/ttbXLSDYNA_library.F
@@ -0,0 +1,52 @@
+! -----------MODULE TENSORXLSDYNA-------------------------------
+ module TensorXLSDYNA
+ use Tensor
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+ ! use this module in the following form:
+ ! ---------------------------------------
+ !
+ ! ---------------------------------------
+
+! ------BEGIN INTERFACE-------------------------------------
+ interface defoGrad
+ module procedure vec9_LSTC_to_unsymTensor_2
+ end interface
+
+ interface ten_to_list
+ module procedure ten_4_to_list_36
+ end interface
+
+ interface list_to_array
+ module procedure list_36_to_array_6x6
+ end interface
+
+ interface sigX_to_ten
+ module procedure sigX_to_ten_2
+ end interface
+
+ interface dX_to_ten
+ module procedure dX_to_ten_2
+ end interface
+
+ interface ten_to_sigX
+ module procedure ten_2_to_sigX
+ end interface
+! ------END INTERFACE---------------------------------------
+
+ contains
+
+! ------BEGIN FUNCTIONS-------------------------------------
+ include './libdefoGrad.f'
+! ------TENSOR for umatV SECTION----------------------------
+ include './libX_to_ten.f'
+ include './libten_to_list.f'
+! ------END FUNCTIONS---------------------------------------
+! ------BEGIN SUBROUTINES-----------------------------------
+ include './libten_to_X.f'
+! ------END SUBROUTINES-------------------------------------
+
+ end module TensorXLSDYNA
\ No newline at end of file