You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
原文:Generalization and width. Neyshabur et al. [2018b] found that wider networks generalize better. Can we now explain this? Intuitively, wider networks have more sub-networks at any given level, and so the sub-network with maximum coherence in a wider network may be more coherent than its counterpart in a thinner network, and hence generalize better. In other words, since—as discussed in Section 10—gradient descent is a feature selector that prioritizes well-generalizing (coherent) features, wider networks are likely to have better features simply because they have more features. In this connection, see also the Lottery Ticket Hypothesis [Frankle and Carbin, 2018]
Based on our theory, finite learning rate, and mini-batch stochasticity
are not necessary for generalization
我们认为较低的学习率可能无法降低泛化误差,因为较低的学习率意味着更多的迭代次数(与早停相反)。
Assuming a small enough learning rate, as training progresses, the generalization gap cannot decrease. This follows from the iterative stability analysis of training: with 40 more steps, stability can only degrade. If this is violated in a practical setting, it would point to an interesting limitation of the theory
谷歌最近出品的82页论文《ON THE GENERALIZATION MYSTERY IN DEEP LEARNING》,在此我简单归纳下论文的思想,有兴趣的看看原论文。
一、DNN泛化能力的问题
论文主要探讨的是, 为什么过参数的神经网络模型还能有不错的泛化性?即并不是简单记忆训练集,而是从训练集中总结出一个通用的规律,从而可以适配于测试集(泛化能力)。

以经典的决策树模型为例, 当树模型学习数据集的通用规律时:一种好的情况,假如树第一个分裂节点时,刚好就可以良好区分开不同标签的样本,深度很小,相应的各叶子上面的样本数是够的(即统计规律的数据量的依据也是比较多的),那这会得到的规律就更有可能泛化到其他数据。(即:拟合良好, 有泛化能力)。
另外一种较差的情况,如果树学习不好一些通用的规律,为了学习这个数据集,那树就会越来越深,可能每个叶子节点分别对应着少数样本(少数据带来统计信息可能只是噪音),最后,死记硬背地记住所有数据(即:过拟合 无泛化能力)。我们可以看到过深(depth)的树模型很容易过拟合。
那么过参数化的神经网络如何达到良好的泛化性呢?
二、 DNN泛化能力的原因
本文是从一个简单通用的角度解释——在神经网络的梯度下降优化过程上,探索泛化能力的原因:
我们总结了梯度相干理论 :来自不同样本的梯度产生相干性,是神经网络能有良好的泛化能力原因。当不同样本的梯度在训练过程中对齐良好,即当它们相干时,梯度下降是稳定的,可以很快收敛,并且由此产生的模型可以有良好的泛化性。 否则,如果样本太少或训练时间过长,可能无法泛化。

基于该理论,我们可以做出如下解释。
2.1 宽度神经网络的泛化性
更宽的神经网络模型具有良好的泛化能力。这是因为,更宽的网络都有更多的子网络,对比小网络更有产生梯度相干的可能,从而有更好的泛化性。 换句话说,梯度下降是一个优先考虑泛化(相干性)梯度的特征选择器,更广泛的网络可能仅仅因为它们有更多的特征而具有更好的特征。
但是个人觉得,这还是要区分下网络输入层/隐藏层的宽度。特别对于数据挖掘任务的输入层,由于输入特征是通常是人工设计的,需要考虑下做下特征选择(即减少输入层宽度),不然直接输入特征噪音,对于梯度相干性影响不也是有干扰的。
2.2 深度神经网络的泛化性
越深的网络,梯度相干现象被放大,有更好的泛化能力。

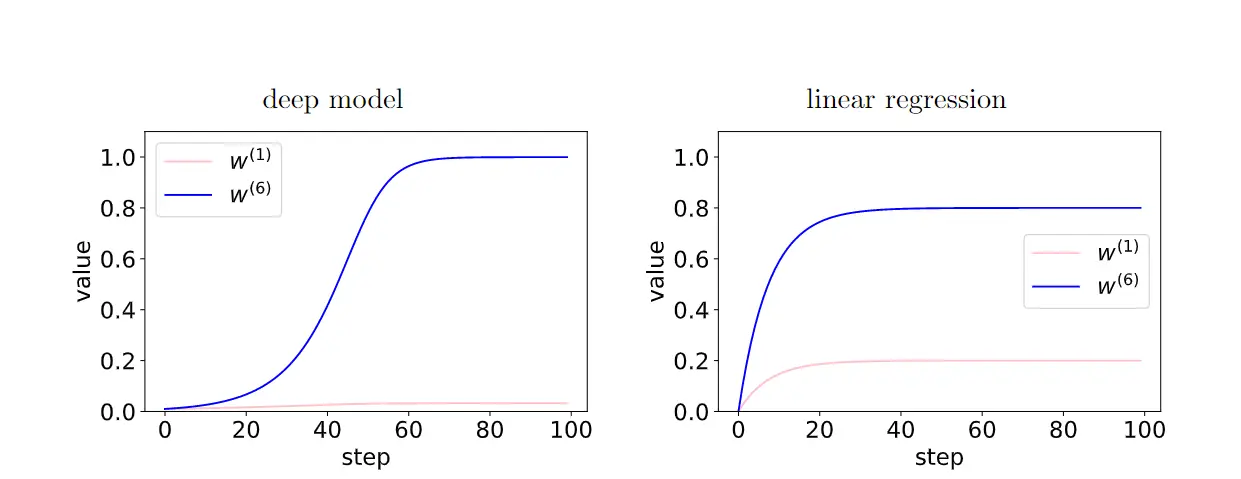
在深度模型中,由于层之间的反馈加强了有相干性的梯度,存在相干性梯度的特征(W6)和非相干梯度的特征(W1)之间的相对差异在训练过程中呈指数放大。从而使得更深的网络更偏好相干梯度,从而更好泛化能力。
2.3 早停(early-stopping)
通过早停我们可以减少非相干梯度的过多影响,提高泛化性。
在训练的时候,一些容易样本比其他样本(困难样本)更早地拟合。训练前期,这些容易样本的相干梯度做主导,并很容易拟合好。训练后期,以困难样本的非相干梯度主导了平均梯度g(wt),从而导致泛化能力变差。

(注:简单的样本,是那些在数据集里面有很多梯度共同点的样本,正由于这个原因,大多数梯度对它有益,收敛也比较快。)
2.4 全梯度下降 VS 学习率
我们发现全梯度下降也可以有很好的泛化能力。此外,仔细的实验表明随机梯度下降并不一定有更优的泛化,但这并不排除随机梯度更易跳出局部最小值、起着正则化等的可能性。
我们认为较低的学习率可能无法降低泛化误差,因为较低的学习率意味着更多的迭代次数(与早停相反)。
2.5 L2、L1正则化
目标函数加入L2、L1正则化,相应的梯度计算, L1正则项需增加的梯度为sign(w) ,L2梯度为w。以L2正则为例,相应的梯度W(i+1)更新公式为:
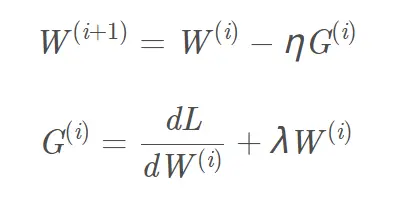
我们可以把“L2正则化(权重衰减)”看作是一种“背景力”,可将每个参数推近于数据无关的零值 ( L1容易得到稀疏解,L2容易得到趋近0的平滑解) ,来消除在弱梯度方向上影响。只有在相干梯度方向的情况下,参数才比较能脱离“背景力”,基于数据完成梯度更新。
2.6 梯度下降算法的进阶
Momentum 、Adam等梯度下降算法,其参数W更新方向不仅由当前的梯度决定,也与此前累积的梯度方向有关(即,保留累积的相干梯度的作用)。这使得参数中那些梯度方向变化不大的维度可以加速更新,并减少梯度方向变化较大的维度上的更新幅度,由此产生了加速收敛和减小震荡的效果。
我们可以通过优化批次梯度下降算法,来抑制弱梯度方向的梯度更新,进一步提高了泛化能力。比如,我们可以使用梯度截断(winsorized gradient descent),排除梯度异常值后的再取平均值。或者取梯度的中位数代替平均值,以减少梯度异常值的影响。

小结
文末说两句,对于深度学习的理论,有兴趣可以看下论文提及的相关研究。个人水平有限,不足之处还望指教,有什么见解,欢迎学习群相互讨论下。
文章首发公众号“算法进阶”,欢迎关注。公众号阅读原文可访问文章相关代码及资料
The text was updated successfully, but these errors were encountered: