-
Notifications
You must be signed in to change notification settings - Fork 1
/
02_MLP
1 lines (1 loc) · 101 KB
/
02_MLP
1
{"nbformat":4,"nbformat_minor":0,"metadata":{"colab":{"name":"EN_02_MLP TODO","provenance":[{"file_id":"1ppufvcv72-uuSP1fUm6SjQ70goJVjRy0","timestamp":1576571071245}],"collapsed_sections":[]},"kernelspec":{"name":"python3","display_name":"Python 3"},"accelerator":"GPU","widgets":{"application/vnd.jupyter.widget-state+json":{"860ff1214beb4c21aa649faeb8e810d1":{"model_module":"@jupyter-widgets/controls","model_name":"HBoxModel","state":{"_view_name":"HBoxView","_dom_classes":[],"_model_name":"HBoxModel","_view_module":"@jupyter-widgets/controls","_model_module_version":"1.5.0","_view_count":null,"_view_module_version":"1.5.0","box_style":"","layout":"IPY_MODEL_355e90d9e3634d18aaaf9906566fb4ca","_model_module":"@jupyter-widgets/controls","children":["IPY_MODEL_892b8d98ed084d90916663c0ecb489e8","IPY_MODEL_b336ef71bdde4b209ab078ed3588ad97"]}},"355e90d9e3634d18aaaf9906566fb4ca":{"model_module":"@jupyter-widgets/base","model_name":"LayoutModel","state":{"_view_name":"LayoutView","grid_template_rows":null,"right":null,"justify_content":null,"_view_module":"@jupyter-widgets/base","overflow":null,"_model_module_version":"1.2.0","_view_count":null,"flex_flow":null,"width":null,"min_width":null,"border":null,"align_items":null,"bottom":null,"_model_module":"@jupyter-widgets/base","top":null,"grid_column":null,"overflow_y":null,"overflow_x":null,"grid_auto_flow":null,"grid_area":null,"grid_template_columns":null,"flex":null,"_model_name":"LayoutModel","justify_items":null,"grid_row":null,"max_height":null,"align_content":null,"visibility":null,"align_self":null,"height":null,"min_height":null,"padding":null,"grid_auto_rows":null,"grid_gap":null,"max_width":null,"order":null,"_view_module_version":"1.2.0","grid_template_areas":null,"object_position":null,"object_fit":null,"grid_auto_columns":null,"margin":null,"display":null,"left":null}},"892b8d98ed084d90916663c0ecb489e8":{"model_module":"@jupyter-widgets/controls","model_name":"FloatProgressModel","state":{"_view_name":"ProgressView","style":"IPY_MODEL_fcf13191a4db47478aaf2d57a1025725","_dom_classes":[],"description":"E: 0.1237, ACC: 59.0%: 100%","_model_name":"FloatProgressModel","bar_style":"success","max":2000,"_view_module":"@jupyter-widgets/controls","_model_module_version":"1.5.0","value":2000,"_view_count":null,"_view_module_version":"1.5.0","orientation":"horizontal","min":0,"description_tooltip":null,"_model_module":"@jupyter-widgets/controls","layout":"IPY_MODEL_51efa94a8eae4152b924941a84ec184d"}},"b336ef71bdde4b209ab078ed3588ad97":{"model_module":"@jupyter-widgets/controls","model_name":"HTMLModel","state":{"_view_name":"HTMLView","style":"IPY_MODEL_d42b681bc7d8424fbf9e40732cca98a1","_dom_classes":[],"description":"","_model_name":"HTMLModel","placeholder":"","_view_module":"@jupyter-widgets/controls","_model_module_version":"1.5.0","value":" 2000/2000 [03:52<00:00, 8.60it/s]","_view_count":null,"_view_module_version":"1.5.0","description_tooltip":null,"_model_module":"@jupyter-widgets/controls","layout":"IPY_MODEL_f47d9e1dffd747569f514c14e36e2b19"}},"fcf13191a4db47478aaf2d57a1025725":{"model_module":"@jupyter-widgets/controls","model_name":"ProgressStyleModel","state":{"_view_name":"StyleView","_model_name":"ProgressStyleModel","description_width":"initial","_view_module":"@jupyter-widgets/base","_model_module_version":"1.5.0","_view_count":null,"_view_module_version":"1.2.0","bar_color":null,"_model_module":"@jupyter-widgets/controls"}},"51efa94a8eae4152b924941a84ec184d":{"model_module":"@jupyter-widgets/base","model_name":"LayoutModel","state":{"_view_name":"LayoutView","grid_template_rows":null,"right":null,"justify_content":null,"_view_module":"@jupyter-widgets/base","overflow":null,"_model_module_version":"1.2.0","_view_count":null,"flex_flow":null,"width":null,"min_width":null,"border":null,"align_items":null,"bottom":null,"_model_module":"@jupyter-widgets/base","top":null,"grid_column":null,"overflow_y":null,"overflow_x":null,"grid_auto_flow":null,"grid_area":null,"grid_template_columns":null,"flex":null,"_model_name":"LayoutModel","justify_items":null,"grid_row":null,"max_height":null,"align_content":null,"visibility":null,"align_self":null,"height":null,"min_height":null,"padding":null,"grid_auto_rows":null,"grid_gap":null,"max_width":null,"order":null,"_view_module_version":"1.2.0","grid_template_areas":null,"object_position":null,"object_fit":null,"grid_auto_columns":null,"margin":null,"display":null,"left":null}},"d42b681bc7d8424fbf9e40732cca98a1":{"model_module":"@jupyter-widgets/controls","model_name":"DescriptionStyleModel","state":{"_view_name":"StyleView","_model_name":"DescriptionStyleModel","description_width":"","_view_module":"@jupyter-widgets/base","_model_module_version":"1.5.0","_view_count":null,"_view_module_version":"1.2.0","_model_module":"@jupyter-widgets/controls"}},"f47d9e1dffd747569f514c14e36e2b19":{"model_module":"@jupyter-widgets/base","model_name":"LayoutModel","state":{"_view_name":"LayoutView","grid_template_rows":null,"right":null,"justify_content":null,"_view_module":"@jupyter-widgets/base","overflow":null,"_model_module_version":"1.2.0","_view_count":null,"flex_flow":null,"width":null,"min_width":null,"border":null,"align_items":null,"bottom":null,"_model_module":"@jupyter-widgets/base","top":null,"grid_column":null,"overflow_y":null,"overflow_x":null,"grid_auto_flow":null,"grid_area":null,"grid_template_columns":null,"flex":null,"_model_name":"LayoutModel","justify_items":null,"grid_row":null,"max_height":null,"align_content":null,"visibility":null,"align_self":null,"height":null,"min_height":null,"padding":null,"grid_auto_rows":null,"grid_gap":null,"max_width":null,"order":null,"_view_module_version":"1.2.0","grid_template_areas":null,"object_position":null,"object_fit":null,"grid_auto_columns":null,"margin":null,"display":null,"left":null}}}}},"cells":[{"cell_type":"markdown","metadata":{"id":"a4h2wC91R1lB"},"source":["# Deep Learning: Multilayer Perceptron\n","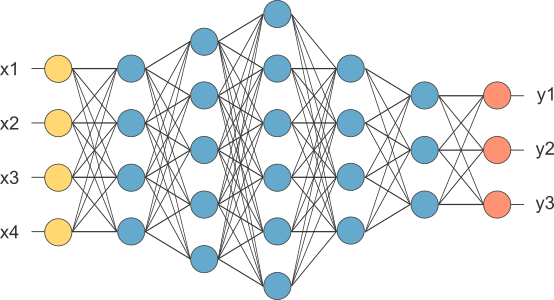\n","\n","\n","$\\renewcommand{\\vec}{\\mathbf}$\n","\n","*Tutorial by* [Alessandro Torcinovich](https://aretor.github.io) @ Ca' Foscari University\n"]},{"cell_type":"markdown","metadata":{"id":"ykF-ZTbdTOmX"},"source":["---\n","## 1. McCulloch & Pitts' Neuron\n","In this tutorial we will see how to build our first neural network, the Multilayer Perceptron (MLP), and how to use it to learn simple, logical functions (AND and XOR) and to classify their input correctly.\n","\n","Nowadays, a neural network (NN) is one of the most used classifiers for the classification of images (and other types of data). The MLP is one of this networks and its history begins in the 1943, when McCulloch and Pitts design the first mathematical model of a neuron, the **M-P Neuron**\n","\n","\n","\n","The M-P takes binary inputs only and outputs a binary number. Its way of functioning is simple:\n","1. Take an input $\\vec{x}$\n","1. Compute the **aggregation function**: $g(\\vec{x}) = \\sum_i^n x_i$\n","2. Compute the **step function**: if $g(\\vec{x}) \\ge \\theta$ then $f(\\vec{x}) = 1$ otherwise $f(\\vec{x}) = 0$.\n","\n","$\\theta$ is the **bias**, the threshold that decides if the neuron \"fires\" ($1$) or not ($0$). It may be learned or set by hand.\n","\n","\n"]},{"cell_type":"markdown","metadata":{"id":"fvcmgzTcgJ0b"},"source":["Let's suppose we want to learn the function AND ($\\land$). First, I build a dataset with binary observations $\\vec{X} \\in \\mathbb{R}^{n \\times 2}$, containing $n$ observations. Each observation $\\vec{x}_i$ is a 2D vector containing the input to the AND function, while the label $y_i$ contains the output of the function. For example, if $\\vec{x}_i = \\begin{pmatrix}0 & 1\\end{pmatrix}$ then $y_i = 0 \\land 1 = 0$."]},{"cell_type":"code","metadata":{"id":"uc5-T_sFhZQt"},"source":["from tqdm import tqdm_notebook as tqdm\n","import matplotlib.pyplot as plt\n","import numpy as np\n","\n","import torch\n","import torch.nn as nn # contains NN related stuff\n","\n","%matplotlib inline\n","device = 'cuda' # change at your taste"],"execution_count":null,"outputs":[]},{"cell_type":"code","metadata":{"id":"cEsI7yRjRkE8","colab":{"base_uri":"https://localhost:8080/","height":127},"executionInfo":{"status":"ok","timestamp":1590663852065,"user_tz":-120,"elapsed":537,"user":{"displayName":"Alessandro TORCINOVICH","photoUrl":"https://lh3.googleusercontent.com/a-/AOh14Gi96E7HK6ff0uWSudqbJvEMactRTPtsT5-4448y=s64","userId":"03260776184459049943"}},"outputId":"4f2e4420-a970-4a69-ed06-bda34e55f814"},"source":["n = 100\n","X = torch.rand(n, 2)\n","X = (X >= 0.5) # binarize the dataset\n","X = X.to(torch.float) # convert to float\n","y_true = X.prod(dim=1) # generate the labels\n","X[:10], y_true[:10]"],"execution_count":null,"outputs":[{"output_type":"execute_result","data":{"text/plain":["tensor([1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 0., 0., 0., 1., 1., 1., 1.,\n"," 0., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1.,\n"," 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1.,\n"," 1., 0., 1., 0., 1., 0., 0., 1., 0., 1., 0., 0., 1., 1., 1., 1., 1., 1.,\n"," 0., 1., 1., 0., 0., 1., 1., 1., 1., 1., 1., 0., 1., 1., 0., 0., 0., 1.,\n"," 1., 1., 0., 0., 1., 0., 0., 1., 1., 1.])"]},"metadata":{"tags":[]},"execution_count":7}]},{"cell_type":"markdown","metadata":{"id":"_WrjJqBXluBt"},"source":["Now let's define our neuron. It will be a subclass of the abstract class `torch.nn.Module`, used to define a NN in PyTorch. When you subclass `Module`, you must overwrite the abstract method `forward` that defines the **forward step** of the model, described before (the **backward step**, instead, is automatic as we have seen)"]},{"cell_type":"code","metadata":{"id":"1zaNXCbmmn-r"},"source":["class MPN(nn.Module):\n"," def __init__(self, theta):\n"," super().__init__()\n"," self.theta = theta\n","\n"," def forward(self, x):\n"," g_x = x.sum(dim=1)\n"," f_x = (g_x >= self.theta).to(torch.float)\n"," return f_x\n"],"execution_count":null,"outputs":[]},{"cell_type":"markdown","metadata":{"id":"sCFfoS3Io1Md"},"source":["Let's also define a function to compute the accuracy of our model"]},{"cell_type":"code","metadata":{"id":"Ibw_P1RyoACk"},"source":["def evaluate(y_true, y_pred):\n"," correct = (y_true == y_pred).sum()\n"," accuracy = 100. * correct / y_true.shape[0]\n"," return accuracy.item() # returns just the value without the tensor wrapper"],"execution_count":null,"outputs":[]},{"cell_type":"markdown","metadata":{"id":"sHSnRNYTqoja"},"source":["Now we're ready to test ou first model with different values of `theta`"]},{"cell_type":"code","metadata":{"id":"Tllf3zziqwAB","colab":{"base_uri":"https://localhost:8080/","height":35},"executionInfo":{"status":"ok","timestamp":1590664061467,"user_tz":-120,"elapsed":445,"user":{"displayName":"Alessandro TORCINOVICH","photoUrl":"https://lh3.googleusercontent.com/a-/AOh14Gi96E7HK6ff0uWSudqbJvEMactRTPtsT5-4448y=s64","userId":"03260776184459049943"}},"outputId":"f3b673cb-862e-4340-e99b-7867494bcab0"},"source":["theta = 2.\n","mpn = MPN(theta)\n","y_pred = mpn(X) # calls the forward method\n","accuracy = evaluate(y_true, y_pred)\n","print(f'The accuracy with theta = {theta} is {round(accuracy, 2)}%')"],"execution_count":null,"outputs":[{"output_type":"stream","text":["The accuracy with theta = 1.0 is 56.0%\n"],"name":"stdout"}]},{"cell_type":"markdown","metadata":{"id":"GImebFP3wdjm"},"source":["The AND function is rather simple to learn. Let's try to adress a more complex problem. In the real dataset, the collected data contain noise that must be filtered. First of all, let's perturb our dataset $\\vec{X}$ with a bit of noise"]},{"cell_type":"code","metadata":{"id":"lWM__mGwy90g","colab":{"base_uri":"https://localhost:8080/","height":219},"executionInfo":{"status":"ok","timestamp":1590664145150,"user_tz":-120,"elapsed":533,"user":{"displayName":"Alessandro TORCINOVICH","photoUrl":"https://lh3.googleusercontent.com/a-/AOh14Gi96E7HK6ff0uWSudqbJvEMactRTPtsT5-4448y=s64","userId":"03260776184459049943"}},"outputId":"22fa08b5-b13d-4bd7-b1bc-1981a68bc0e0"},"source":["a, b = -2e-1, 2e-1 # floats in scientific notation: 2e-1 == 2 * 10 ** -1\n","eps = a + (b - a) * torch.rand(X.shape) # random noise between in [a, b)\n","Xp = X + eps\n","# treshold values over 1 and under 0\n","Xp[:10], y_true[:10]"],"execution_count":null,"outputs":[{"output_type":"execute_result","data":{"text/plain":["(tensor([[ 1.1338, 1.1784],\n"," [ 0.9988, 1.1834],\n"," [ 0.0504, -0.0511],\n"," [ 0.1258, 1.1844],\n"," [-0.0301, 0.9202],\n"," [ 0.9319, 0.0445],\n"," [ 1.0381, -0.1305],\n"," [ 1.1849, 0.9630],\n"," [ 0.8277, 1.0292],\n"," [ 0.9996, 1.1195]]),\n"," tensor([1., 1., 0., 0., 0., 0., 0., 1., 1., 1.]))"]},"metadata":{"tags":[]},"execution_count":14}]},{"cell_type":"code","metadata":{"id":"q_hoperHc8bE","colab":{"base_uri":"https://localhost:8080/","height":281},"executionInfo":{"status":"ok","timestamp":1590664149057,"user_tz":-120,"elapsed":775,"user":{"displayName":"Alessandro TORCINOVICH","photoUrl":"https://lh3.googleusercontent.com/a-/AOh14Gi96E7HK6ff0uWSudqbJvEMactRTPtsT5-4448y=s64","userId":"03260776184459049943"}},"outputId":"791c0226-19dd-4aec-fffc-803e764c8794"},"source":["plt.scatter(Xp[:, 0], Xp[:, 1,], c=y_true)\n","plt.title('Noisy AND')\n","plt.show()"],"execution_count":null,"outputs":[{"output_type":"display_data","data":{"image/png":"iVBORw0KGgoAAAANSUhEUgAAAXwAAAEICAYAAABcVE8dAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOzdZ3RU1deA8WdPT6UXpXdBBNFgQ2yIgmLBhtgrNvyLiopiRX2xYwMVO9gFC6KCjWIBJIogXUC6QEhC+vTzfpgQMplJgUwSSPZvLZfJvXfu2WEl+557qhhjUEopVftZajoApZRS1UMTvlJK1RGa8JVSqo7QhK+UUnWEJnyllKojNOErpVQdoQlf1Vki8q2IXFnTcShVXTThqwOWiKwXkR0iklDs2HUiMrsinzfGDDTGvFsFcYmIrBOR5VHOzRYRt4i0KnbsVBFZX+z79SJSICI5IrJLRH4TkRtFRP9eVaXoL5A60FmB22o6iBJOAJoC7UWkd5TzecAD5dzjLGNMEtAGeAK4B3gzplGqOkcTvjrQPQ2MFJH60U6KyHEislBEsgr/f1yxc7NF5LrCrzuKyJzC63aKyMeFx8eLyLMl7jlNRG4vI6YrgS+Bbwq/LulFYKiIdCjvhzPGZBljpgFDgCtFpHt5n1GqNJrw1YEuFZgNjCx5QkQaAl8TSrCNgOeAr0WkUZT7PAp8BzQAWgIvFR5/l1BythTeszFwKvBBtGBEJB64AHi/8L+LRcRR4rItwOvAIxX9IY0xvwObgb4V/YxSJWnCV7XBg8CtItKkxPEzgX+MMZONMX5jzIfASuCsKPfwEWo+OdgY4zbG/AJFiTYL6Fd43cXAbGPM9lJiOQ/wEHp4fA3YC+MoaSxwlogcWtEfEtgKNNyL65UKowlfHfCMMUuB6cCoEqcOBjaUOLYBaBHlNncDAvwuIstE5Jpi594FLiv8+jJgchnhXAl8UviAcQNTidKsY4xJA14GxpRxr5JaABl7cb1SYWw1HYBSMfIQ8CdQvL19K6Fae3GtgRklP2yM2QZcDyAixwM/iMhcY8wa4D1gqYj0BLoCX0QLQERaAqcAR4nI+YWH4wGXiDQ2xuws8ZGngXXA7+X9cIWdvy2AX8q7VqnSaA1f1QqFiflj4H/FDn8DdBaRS0TEJiJDgG6E3gbCiMiFhQkbIBMwQLDw3puBhYRq9lONMQWlhHE5sBroAhxe+F9nQm3vQ6PEvIvQA+ru0n4uEUkWkUHAR8B7xpi/S7tWqfJowle1yRigaEy+MSYdGATcCaQTSqyDotS0AXoDC0QkF5gG3GaMWVfs/LvAYZTfnDPBGLOt+H/Aq0QfrQPwAhCIcvwrEckBNgGjCXU4X11G2UqVS3QDFKXKJyInEGraaWP0j0YdoLSGr1Q5RMROaHLXG5rs1YFME75SZRCRrsAu4CDg+RoOR6lK0SYdpZSqI7SGr5RSdcR+Ow6/cePGpm3btjUdhlJKHVD++OOPncaYkrPOgf044bdt25bU1NSaDkMppQ4oIlJydnkRbdJRSqk6QhO+UkrVEZrwlVKqjtCEr5RSdYQmfKXUfs8EdmK8CzGBbTUdygEtJglfRN4q3Ex6aSnnLxWRJSLyd+GGzD1jUa5SqnYzJkAw6z5M2kmYzBsxaf0JZt6KMZ6aDi2CMT5MIA1jfDUdSqliVcN/BxhQxvl/gRONMYcR2kpuYozKVeUIBoPM+yqVZ66dwIQRb7F28foyr/f7/Hjd3uoJTqlymLyJUDAd8ILJATzgmY3JfnLv7mMMxvsXJu9NTME0Sl/heh9iNIZg7gTMjqMwaadgdhxFMPc19sdVDGK2tIKItAWmG2PK3GRZRBoAS40x0XYdKpKSkmJ0HH7lBAIBHjznKZbMXY47143FasHusDHsmSs4+6bTw67N2pnN8zdMZN70VEzQ0KV3R+5840badGtVQ9ErBcEdx0Ew2mrWTqTZYgq3Gi6TMT5M5s3g/R3wgTgAO9LwPcTepfIx5r0DOeOA4g+ROEi6C3Gdhsl7E7zzwHowknA94jiy0mWWRUT+MMakRDtXE2341wLfRjshIsNEJFVEUtPS0qo5rP1ffk4BeVl5Fb5+3rRUlsxZhjvXDUAwEMRT4OW1O98lOyOn6DpjDHee/DDzp6cS8AUIBoKsXLCaEcc/QHZ6Tmm3V6rqBUv7/fMB/grdwuR/DN4FhBKyH0w+mCzMruGxqYXnvUZ4sif0fd7LmJ2DIP898K8Ez0+YjKsJ5n9Z+TL3UbUmfBE5mVDCvyfaeWPMRGNMijEmpUmTqDOD66QdG9MYecrDnN/4ai5oei3Dj76XjSu3lPu5OZ/Ow50X2dZps9tY9OOe7pYlc5ezY0Maft+efTiMAZ/Hx4y3Z8Xmh1BqXziOiH7c1hERR8XuUfAp4I48HtgOgVInpVaIMQaC6dFPBjPB5BJ6OO3mhpzHMKZiD6tYq7aELyI9gDeAcwp3IlIV4Pf5ue34B/j75xX4fQH8vgCrU9cw4vj7ycvOL/OzcYkuxCKRJwRcCc6ib7eu2UYwGFnT8RR42bh8U6V/BlU3GeMjmPsmwbTTCO44iWDOU5hSa+zRSdJ9IPHsWQXGCsQhyY/sxV2ibSgGoT3rSztXMSIC1nalnLUS/S3EB4GNlSp3X1VLwheR1sBnwOXGmNXVUWZtseDrP8nLyiMYCBYd2137nv3Rr2V+duC1/XC47BHHLRYLvfodVvR9+x5tkCjPBVeCky69O+578KpOM7tuhdwXILAeglsh711M+gUYU/FBAWLvgjT6CuKGgO0wiDsXaTx179rBXYMBV+RxS32wtq/4fUqLMfneKPd3gbWU/i/jD5VdA2I1LPNDYB7QRUQ2i8i1InKjiNxYeMmDQCNggoj8JSLaG1tB2/7dgc8TWUtw53nYsqbsMcldj+7E5Q9eiN1lJy7RRXxSHAn14nls+r04nHseBJ1TOtA5pQP2Yg8Hq81CfHI8p15+Qux+GFVnGN9y8PxGeFOKD4LbwR21C69UYmuFpd5DWBpPxVJvLGLbu0qIJFwG9m6FbwoALpAEpP6LoRp6JYnzJKTBa2A/HKQ+2HshDV5Hku4A4kpc7QDHcYilYdhRYwzGVO5toyJislqmMWZoOeevA66LRVl1Tcde7bA5bPi94Uk/LtFFl5QO5X5+yN3n0v+KE1n041JcCU56Dzgchyu87VNE+L9v7uPdhz5h5juz8Hv8HHPWkVz/1OXEJZb8hVWqAnxLoh83+RhvKhJ3TsyKMsEMTO5E8PwAkoQkXAGuc4uSuYgTGn4A3l8w3oWIpRnEDUJiWMsW57GI89jI2BL/hdwJIDYwPrD3grhBmPwPQ1/b2mKyn4CCqYAXY+uO1BuD2A+NWWxhce6PY0VBh2XuZozhtj6jWfvXerzuUOePzWGjedumTFzyDHZHZJNNLHk9Pr5/dzY/T51PYv0EzrrpdHqeVDW/jKr2MJ45mF0jwJQcVeaExOFYEm+ITTnBXMzOMwuHbu7uHI2D+AuwJD8QkzIqywRzwb8WY/Jh1+2AB3bX5iURTDZQrJlL4pHGXyPWMkeul6qsYZma8GNg+fzVvPvQx6xfuonWh7TgykcuovvxXWN2/4I8N+8/NoXvJ80h6A9ywkXHcdWYISQ1SIxZGdH4vD5u7/sAG5ZvLhrt44x3cun95zN01OAqLVsd2IzxY9L6hZpw2NP/FEpmPyDWxqV/NrgLCqZjgtsR+xHgPAERa9Rrg7lvhvoJIkbhOJEmPyDWZnvuG9gGnl9AXOA8CbFU7d9PccYYzM6BEPgXKC/n2iH+UizJ9+1TWXU24W/fkMZfs5aSWD+B3gN7hbVbx8ri2csYfeb/4SnY84R2xjl46LO76H364TEvrzp9P2kOL97yesTQTofLzgcbX6Ve4+QaikwdCExgC2bX7eBbDghYmyP1nkEcpa+sYryLMZlXFdaA3UA82DsjDSchEtnxGsy4DrxzI28kiUi9pxFXv9B1uRMh9yUQC6GuS4PUn4A4j4vBT1o+49+A2XkWUYeHRmM/BkujSftUVlkJf7/d8aoyjDG8ce/7fPHiN1isFiwWwWqz8sR3D9D5yPLbvffGK3e8E5bsITScccKIt3l7xQsxLau6/fLFgujj+B02lsxdQd/zjq6BqNSBQqwtkEafYALpgBcszcvsJDXGRGkGygffSkzeJCRxWOSHrC0JDX8s2eEZBGvT0H19f0Puy4SaUoqVt+tmaDoPkdj2U4Uq0QFEiqdXX+hhU6H6tQMch5V/2T6olatlpn63mGnjZ+B1+3DnecjPcZOTmcfoM8cSCMS2J3z90ujjaTev2kowGIx6bn+WnZHD/Ol/sOy3VSQ3SsISZRy/MZDUIKEGolMHIrE2QqwHlT8iJrABghlRTrih4Ivo9064DCj55m4FawuwhVZ5MfmfEdZGXsQCnihvB/vImGBoDZ0dvTHbDyWY1g/j/qkwpPYg0f5mLKF4iwiIA4m/PGZxFVcra/jfvP591Jqpt8DLinmrY9q+Xq9JPTL+y4w4ntQwEYvlwHqefvzUF0x6+BPsDhtBY4hLcGFz2Io6i3eLS3Rx2Amx+zdUKiTU1BJVKW34YusI9V/AZN8HpiA0xt1+WIkhl27C+hF2Mwb2Yk5AeUzuS5D3FkXLLAQ2hd5YGrwWGsFTfxwm8/rC5ipvaJiotS04jgmN0jH54OiNJN+PWJvHLK7iamXCL8gtZelUIaL5pbIuvucc3rzvQzz5e8p0xju5cOTZMS2nqi366W8mj5mC1+0rSvDuXA9JjRIREax2K8YYEpLjGTvjfqzW6H+ASu0zayuwHlTYsVmcC+IuKPVj4joZnL+GJnhJIlLYlLPn/ECM+9tQQg3jB2efmIRujBfyiyX7Im5M7guhYZuOo6Dx95iCzyCwDXEeA85+iNgheVRM4ihPrUz4/S7py7JfV0bU8oOBIIf2OaRC9/AUeJj14a/8+ePfNG/bhDOH9adZm8j1fc699QyyM/KY8uw0IFRpOPfWgQy5O3bjjKvDl+NnhD20INQW6XP7+L9vR+Mp8JKQHMchR3c64N5cVNUwvlWY3OfBt7hwJchbQsl3H4kI1H8Jk3EpoUXOvIANHClI/CXlfNYCtlJmzTr6guMk8MwilJCtgB2SRkVMgNpnwYzQH380/vV74rQ2RRJvjH5dNaiVCf/koX2Y+c4sVqWuxZ3rxmq3YrNZueP1m3DFO8v9fO6uPIYffS/pWzNw53mwOWx8/uI3jPnyHnqdEt6ZIiJc+fBFDB11Lun/ZdKweX2cceWXsb/JyciNelwsFgL+wAE/4kjFlvGtxGRcHGpGwUBwJ2bXCEzy/Yj1IEze26Gx8c5TkIQrKzzJSeydoenP4P4egjvAfgTYD6/UjNjQg2QceOdh3N+BJQFxnYvYO+3zPSNYGoaanaLl/L2cGVyVau2wzEAgwILpfzLvq4XUa5zMgGtOoWXngyv02bdGf8CU56bj84S3XTdq0ZAPNrxSK2u4n7/0DW/e+z6e/PAmL2e8g0+3v0lcQpS1SFSdFcy4AbyzicxwTkJt8bubNhxgaYg0/gqx1KvOEKtdaOjneMKbdVxIw7erfA384urcsEwAq9XKcef05rhzeu/1Z+d+Oi8i2QPkZuaxde12WnY6KBYh7lcGXtuPb9/4ka1rt+PJ9yAWweFycNO4KzXZq0j+JUSvzpbsP/NCMBOTPxlJHF4NgdUcSbgeI0mQ90ro7cbWCUm6t1qTfXlqbcKvDGcpzT7BYBBXfAXX4I6hnMxc3n9sCj9PXYAjzsFZN57GObcMwGqLXcepK97JS/P/j+8nzeXXL3+nQbN6nHPzAF0tU0VnaV76OvARPOCeA7U94YsgCUMhocylxWqUJvxisjNy+ODxz0jbnI6IhO2GY7FaaH9Yaxq3aFStMbnzPdzSexQ7N6fjK1xA7a3RH7Dst1U88PEdMS3LGedk0A39GXRD/5jeV9U+kngzZtdIwpsvHIQmQEWZ61Ji5IyqGbWvMXof7U6s08bPICcjtyjZW20W4pJcNGnViAc/vbPa45r14S9kbt9VlOwBPPleFkz/gw0rNld7PEoBiKs/JI0CSSa0BLAT4s4HWxfCJxIBxCEJV1V7jCqS1vAL/fjeXHbtyApLrACIMPzFazj18hNrpLN28exlUSeRiUVY9fsa2nRtWebnA4EAX748gy/HzyA/p4CjzziCq8YMqfY3FVX7WBKGYuIvDC2QJg0QSzxB/xbIvBwCWwklfhsk3Ys49r4vTcWeJvxCi+csj5pYHU47Fqu1xkbmHNShGXanLWITFLEITVqVn7THDXuN2R//VjTG/ofJc1jw9Z+8uXwcyQ2TqiRmVXeI2ELLGFC4DHDm9YXLIwQJbSFoEFspOz+paqdNOoUO7tAMuyP6869Jy5qrDZ9x3akRnbMWq4X6TeqVuy79jo1p/PThL2ETqgL+IPk5BUx/7fsqiVfVXSbvbQhsKjajNbTipckaiTHFt+j0YPKnEMy8kWDWaIxvWfh9jMG4ZxBMv5TgznMI5k4IPUxUpWnCL3TGdf2w2iMTa4Pm9at93ZjMHVlk7sgCQg+bsTPup3m7pjhcduxOG12P6cSzsx8p961jzaL1UR9i3gIvS+Ysr5LYVR3m/pbIYZmEJmf514a+NG5M+kWYnEfB8xMUTMWkDyWYP2XP5TlPYbLuAd9C8K+A3Fcw6edjTMllC/ZvJphBMOc5gjsvIJh5K8b7V02HpE06uzVt3YT/+2Y0T17xErt2ZBEMBunSuyP3fTCiKLG68z3M/yqVnMw8ep3SvcITuSpq48ot/N8lz7OxsDO2ddeW3PfBCLr3OYRJa14mbXM6Dped+k0qNoGlWdsmBPyRi0ZZbVZadYlt7EpR2jLDJhDadAQw+VPA/y971oUPhr7OfhTjOgNMDuS/R/iDwwOBbZj8L0LDHg8AJpCGST8bgjmAF/x/h3YBq/c4lrizaiyumCR8EXkLGATsMMZ0j3JegBeAM4B84CpjzJ+xKDuanMxcfpg8h40rttA5pQMnXdynQpOHDuvblcnrxrNj404ccQ4aNN2TWFf+/g+jTn+MYDBIMBDEBA0Dr+3HLS9eE5ONkN35Hm7ve3/hCKHQsXWL13N73/t5b/0rxCW4aNqqMcYYfvrgZz574WvysvI59uzeXHzPuSQ3imyP79CzLW0Pbcnav9bj9+0ZKmdz2Dhn+MBKx6xUcRJ/KSb7EcKHalrA1nZPO757BlE3ARFraE0ek124/2vJN4UC8M7Zr8e4F2fyXoVgFrC7780QerCNwbgGhBZMqwGxatJ5BxhQxvmBQKfC/4YBr8So3AgbV27hio7DefO+D5n+2vdMGPE213QdQca2yCWMoxERmrVpEpbsA4EAD5z1BHlZ+RTkuPHke/G6fcx8Zxbzp/8Rk7h/njIfr8cftv6SMeD1+Pll6gIA0v/L5NpuIxh72YusWriWzav/4/MXvuamI+8mL7vkSoAh//ftaFIG9MLmsGF32mnerimPT7+3Vs4WVjUs7lyIGwg4Q0v/SgJYmiL1x++5xlLaLmlBsCSCpRHRZ/BawL+B4M7zCGY9gPFviH38seSZy55kX5wvtO5/DYlJDd8YM1dE2pZxyTnAJBMa3D5fROqLyEHGmP9iUX5xz133Cnm78ovG0bvzPPg8fibe/R6jJt26T/dcMW81HnfkssruPA/fvvEjx54VddmKvbJj4048UUYJefI87Ni4k4I8NzcfeTcZ23aFnff7AuzakcW3b/zIBXdEviomN0zi0S/vIS87H0++hwbN6sfkjUSpkkQsSL0nMAk3gm8RWJqC45iw/Wgl/lKM51fC3wIEpEHhhiUmlPQDJdewDxYumxwE/3KM+yto+D5iL3vgQo2xNIye2I0fpObWFKquTtsWwKZi328uPBZGRIaJSKqIpKalpe11IV63lxUL/qHkgnABf4B50xbu9f128/sCpSZJb5Q1d/ZF594dcCVELungSnDSuXcHZn3wCzm78qJ8ErxuH6nfLS7z/gnJ8TRs3kCTvapyYmuLxA1GnH0iNh8XZx9IvIHQW0Bi4VtAM6Thm6GlCcSCNHgXbJ0AV+EuUbvTVHDP/00+JvvhavuZ9pYkXENoQlpxhUs9WyOXWa8u+9UoHWPMRGNMijEmpUmTvf9HEYsgUbbkA7DZ9/1lptuxnSMeIhBKxh17tePu/mO4ouNwnrjiJTb/s28vLUf270Hrri1wuPa07dlddlp3bcGR/Xuw+o+1+NzRHy4iQvO2NfdLpNTesCTejDSdg9R7EmkwEWkyGym2lr3YWmJp/BXSeBo0mETU3aoAfEuqJ+B9IK7TIXEYRQ82XGDvidQfV+bnjDEY32qMb0XYUNZYqa5ROluA4rMvWhYeiym7w85RA3vx+zeLCPj3dFI6XHb6X3HCPt/X4XJw9zvDeeKyFwkEgvi9flyJLg5q15TPX/wab0EoEW/fkMZvX/7OywueoPUhES8wZbJYLDz908N8/NSX/DBpDgCnXn4CF48ajMVioU23ljjjHRHLF0OoE/bcW8/Y559PqcoyxoD3dwhsBHtXxB4xdiOMWBqCq+w1m8TWFgGChRO4opSKMW5E9s/VXC2Jt2DirwD/ylBfhq1Nmdcb33JM5s1gMgk1cyVA/RdjutpmzNbDL2zDn17KKJ0zgeGERukcDbxojDmqrPvt63r4mTuyuOPEB0nfkkEwEEQsQvuebXhi5gOVXuZ3+4Y0vnt3Nlk7s0k5vSdPXzWe7PTwCSEiQp9zj+KhqSMrVVZJubvyuLzDLWH9ExCaK/DAp3dy/Lll/nMqVWVMMAOTfhkEt4ZGGghg64E0fD0myTi4rTvRNyEXpGkqYjnwZ4ybYD4mrW9oWGpxEo80+Wmvduaq8vXwReRD4CSgsYhsBh6icCt5Y8yrwDeEkv0aQsMyr45FudE0aFqPN5eN46+flrJlzTba92hDt2M7x6TtulmbJlz+4IUA7NySHrW2bYxh6a8rK11WSYn1E3jxt8d57rpXWT5/NSJCjxO7cc/kW2nUvEHMy1OqokzW6NB+srtHpRjA9xcm9yUk6a7KF+AcAJ5pkcetnSKSvfH9A74/wNIEnCfU2PDHkowxUXOQCeZh8t6Ego/ARJlNbAJQMB0SrohJHLEapVPm4NjC0Tm3xKKsirBYLBxxag+OOLVHlZWRUD+BYDD621HDgyq2ndveatWlBeN+fhSvx4fFIpXql1AqFozxgmcOkUMQPZA/FWKQ8CX5Lkz6b4WTmDyAHcSB1B9bLI4AJusucP9Q+CFraLJXw/fD+gdCqchfLQ8CYwwm/13IfQVMJsbaGkm6D3GdUnjeF9om0r+eqDOUAfBggmnEaqjFftVpeyCJS3Bx8tA+OOLCN0RxJjgZOmpwlZbtcNo12av9RIDo7esAsRnBJtZmSOOZkHQnuAZCwg1I4xmIfc/+0qZgKrh/JDSpyw0mD4IZmMxQPdMYQzDvbcyOozHbuxPccRLBgm9jEl9pTN5EyBlX2CYPBDaG9v31/Br63vNDaO2hUpM9oSYdx9Exi0mzRiXcNuF6fB4/v3y2AJvDigkaLnvwQk4a0geA7PQc8rLyadqmMVZr7HanUmp/IRKHsXUD/98lzljBeUrsyrEkFa6pf1X0C/I/InxsP4CBwBaMfwPGPTN8v9ngVsi6ByMuxHVyzOIsKtn4IO/VKDG5MbnPI84+GM/CYgvNReMC22HgOC5mcWnCrwSHy8F9799GdkYOGf/t4qD2TXHGOcnJzOWJy19k0Y9/Y7VZccY7ue2VYfQ9L3ZPaqX2F1JvLCZjKBgfoRp2HFiSYtN+X1EmWqcuIJbQomt5rxE9+Y6rkoRPMDs0ySoa/7+h/1tbENr0vWQN3wKWlpBwFRJ/ESKxa4iptQk/c0cWGEODZlXTnl5ccsOksLXlHx78NMvnr8bv9ePz+HHneXjyihdp2noMXVI6VHk8SlUnsXeGJt9j8j+DwNrQCJ24sxFLQvUFETeosAZfInlKQmj/XRNl/R4obFKpApZ6II4oawIBhX0KEj8Yk/dyiWsELA2RJt9WST9DrWvD37x6Kzen3MOlbW7k0rY3M6znnfy7dGO1lb9lzX+sXLgGf4mds7xuH1Oe+6ra4lCqOomlIZbE67DUG4slYWj1JntA4q8AWwcgvvCIAyQOqfccYkkOre0TjbV99OOVjUdskHgzkbNtXUhiaC9qsTREGrwD1paAKxSz7RCk4QdV1qlcq2r4ngIPI/o+QPbOnKKx6uuXbuSOEx/k/fWvEJ9UyvKtMZS+NRO7w4a3IPwV0wQN29Ztr/LylaqLxBIPjT4F9/cY7zywHoTEnYdYmwNgEkdAzlOEN+u4kKSq26da4q/BEA95EyC4E6ztkOR7Eecxe65x9ITGP0JgM4i9KN6qUqsS/q9fLMRb4A2bmGQM+L1+Zn/8G2dc16/KY2h3WGt8UdbXsTttHH5K2bMPlVL7TsQOcWcgcZGzzi0JlxKUOMh7CQI7wNYeSbobccauQzQyHgmt31/Oks4iAtW0DWStSvg7Nu7EG2W9GXeeh7RNO6slhqQGiZx/+yA+f/Gboj1yLVYLrngnA6+t+geOUio6S/x5EH9ezO5nvIsw+e9BMBOc/ZH4wfvtMg+71ao2/C69O4QtPrZbXKKLLr07VlscVz82lNtfu4GOvdqS2CABi0Xwenxcd9gdPH3N+JitsKmUqhnBvPcwGVeCezp4f4GcJ0JbN5bWObyfqFUJ//CTu9O+R5uwpO9w2WnR6SB6Dzy82uIQEU65pC+XP3QRPo8fvy+AJ9+Lz+1j9se/8eItr1dbLEqp2DLBHMh5ktAQ1N3NxwXg34DJ/7wGIytfrUr4IsK1T1xCo4MbIhbB5rBx3LlH8dzcMTUy8emDxz/Dkx8+LMtb4OWnD36hIPfA2pBZKVXI9xdEHUVTAJ6Z1R7O3qhVCX/5vFXcO+D/+G/ddkzQ4Pf6mTdtIQu+js02hHsrbXN61OMWi4WsnTlRzyml9nOSRPQ1+gUs+/dChrUq4U+8e3JEjdqT7+XVO96NuoFJVTv0uM5RN2SxO2w0admo2uNRSsWAvWdoS8aIJc1cSPwlNRFRhdWqhL/2r/VRj+/akU1+TvU3oVw55mJc8c6wpAXyiAEAACAASURBVO+Md3L9U5dhtenaOkodiEQEafgWWA4KzeSVRMAJSSMQR28AjH8NwaxHCWbeRDDvA0ywrDVzqk+tGpbZ6OCGbImyxaDDZY+6X2xVa9O1JS8tGMu7D33MinmradKqEZeOPp+jz4zdDjZKqeontnbQ5CfwLQaTBfYjQjN6AeP+EbPrdkKrhQbA8xsm/x1oNLXGN2upVQn/0vvP54WbXg9r1nHGOxl82xk1tlplm64tefCTqpvNp5SqGSIWcPQKO2aMH5N1L6ERPLsVQOA/TN47SNKte64N7gLvn2BJAvuRMV0krTS1KuH3v/xEstNzmPTwJ4V72gpn33w6Vzx8UU2HppQ6wBjjBe+80MJrjmMQS73yP+T/h+j7AHjAPQMKE34w703Ieb5wtI8JdQQ3fBuxVe3iirUq4QOcP2IQ59wygF07skhulITD5Sj/Q+UIBAL8PXcFORm5dD/+kGpZgVMpVXOM909M5jBCG7wAxo9Jvh9L/JCyPygJoW0JoylszjHehZDzIuDZs1KmycdkXANNZlVpTb/WJXwAm91G4xaxGQWzceUW7u4/hvzsAgTw+fwMuftcrtyP3xoK8tz89P7P/P3zCg7u2JwzrusXs38PpWo7Y9yYzOsi95jNfhxj7xVaDroUYmuNsbUD/yrCh27GIfGXh+6f/z7hTT4ABkw2+JaAo+omicbkUSIiA0RklYisEZFRUc63FpFZIrJIRJaISOTqRvshYwz3nfE4GVszKMgpID+nAJ/bx5Rnp5H63eKaDi+q7PQcrj/sDl69811+fP9nPnric67pOoLl81fXdGhKHRg8c4m+baMvtJViOaTBhNCSxxJfOILHAfEXgasw7QV3lXJ/AVO183MqnfBFxAqMBwYC3YChItKtxGX3A58YY3oBFwMTKltudfjnz3Vk7cyh5BB+d56HaRNm1ExQ5Zj8yKekb80sWrjN5/FTkOvmqSteqpG5CEodcEwe0RNyIFQLL4dYWyCNv0cavInUG4s0+QFL8ujQqpgAzgFErpNPaIcse6/I4zEUixr+UcAaY8w6Y4wX+Ag4p8Q1Bkgu/LoesDUG5Va5ghw3ligTpwByd+VVczQV8/PnCyI2XwHYsTmdjG27aiAipQ4wjuOib08o8YjztArdQkQQx5GI6/SINe4lfnDhrle7k74ALkgahVgSKxV6eWLRht8CKL5P2Gag5OatDwPficitQAJwarQbicgwYBhA69atYxBa5XQ5qiPBQOQUame8gxMvqrp1tCvDGWW1UACCBruzVnbZKBVTYm2GSbwZcl+jaIE0iQd7b3CeWPn7ixMafQQF0zDu78DaEIm7JLQZShWrrpm2Q4F3jDEtgTOAyRKlK9oYM9EYk2KMSWnSpEk1hVY6V7yT/024HmecA4s1FK4rwUmrLi0YcHUVbHwcA4NuPA1nfPjIJIvVQtdjO4ftu6uUKp0l8Wak4dsQdx64zkDqPYk0eDVmI2hEnEj8hVgavo6l3pPVkuwhNjX8LUDx7VpaFh4r7lpgAIAxZp6EdgloDOyIQflVqv/lJ9K+Rxumv/odmdt3cezZvTl56PE4nFWz52RlnXfbmSyft5qF3y5CLIKI0KB5fe59/7aaDk2pA4o4jkAcR9R0GDElle3IExEbsBroRyjRLwQuMcYsK3bNt8DHxph3RKQr8CPQwpRReEpKiklNTa1UbHXZ+mWb+OePdTRp1YgeJ3bDYqlVyyYppUohIn8YY1Kinat0Dd8Y4xeR4cBMwAq8ZYxZJiJjgFRjzDTgTuB1EbmdUAfuVWUle1V5bQ9tRdtDq2efTKXUgSEmvXjGmG+Ab0oce7DY18uBPrEoSyml1L7R93yllKojNOErpVQdoQlfKaXqCE34SilVR2jCV0qpOkITvlJK1RGa8JVSqo7QhK+UUnWEJnyllKojNOErpVQdoQlfKaXqCE34SilVR2jCV0qpOkITvlJK1RGa8JVSqo7QhK+UUnWEJnyllKojNOErpVQdoQlfKaXqCE34SilVR8Qk4YvIABFZJSJrRGRUKddcJCLLRWSZiHwQi3KVUkpVnK2yNxARKzAe6A9sBhaKyDRjzPJi13QC7gX6GGMyRaRpZctVSim1d2JRwz8KWGOMWWeM8QIfAeeUuOZ6YLwxJhPAGLMjBuUqpZTaC7FI+C2ATcW+31x4rLjOQGcR+VVE5ovIgGg3EpFhIpIqIqlpaWkxCE0ppdRu1dVpawM6AScBQ4HXRaR+yYuMMRONMSnGmJQmTZpUU2hKKVU3xCLhbwFaFfu+ZeGx4jYD04wxPmPMv8BqQg8ApZRS1SQWCX8h0ElE2omIA7gYmFbimi8I1e4RkcaEmnjWxaBspZRSFVTphG+M8QPDgZnACuATY8wyERkjImcXXjYTSBeR5cAs4C5jTHply1ZKKVVxYoyp6RiiSklJMampqTUdhlJKHVBE5A9jTEq0czrTViml6ghN+EopVUdowldKqTpCE75SStURmvCVUqqO0ISvlFJ1hCZ8pZSqIzThK6VUHaEJXyml6ghN+EopVUdowldKqTpCE75SStURmvCVUqqO0ISvlFJ1hCZ8pZSqIzThK6VUHaEJXyml6ghN+EopVUdowldKqToiJglfRAaIyCoRWSMio8q47nwRMSISdb9FpZRSVafSCV9ErMB4YCDQDRgqIt2iXJcE3AYsqGyZSiml9l4savhHAWuMMeuMMV7gI+CcKNc9CjwJuGNQplJKqb0Ui4TfAthU7PvNhceKiMgRQCtjzNdl3UhEholIqoikpqWlxSA0pZRSu1V5p62IWIDngDvLu9YYM9EYk2KMSWnSpElVh6aUUnVKLBL+FqBVse9bFh7bLQnoDswWkfXAMcA07bhVSqnqFYuEvxDoJCLtRMQBXAxM233SGJNljGlsjGlrjGkLzAfONsakxqBspZRSFVTphG+M8QPDgZnACuATY8wyERkjImdX9v5KKaViwxaLmxhjvgG+KXHswVKuPSkWZSqllNo7OtNWKaXqCE34SilVR2jCV0qpOkITvlJK1RGa8JVSqo7QhK+UUnWEJnyllKojNOErpVQdoQlfKaXqCE34SilVR2jCV0qpOkITvlJK1RGa8JVSqo7QhK+UUnWEJnyllKojNOErpVQdoQlfKaXqCE34SilVR2jCV0qpOiImCV9EBojIKhFZIyKjopy/Q0SWi8gSEflRRNrEolyllFIVV+mELyJWYDwwEOgGDBWRbiUuWwSkGGN6AFOApypbrlJKqb0Tixr+UcAaY8w6Y4wX+Ag4p/gFxphZxpj8wm/nAy1jUK5SSqm9EIuE3wLYVOz7zYXHSnMt8G20EyIyTERSRSQ1LS0tBqEppVT1CAQC/DVrKXOnzCNjW2ZNhxOVrToLE5HLgBTgxGjnjTETgYkAKSkpphpDU0qpfbZp1RbuPnUMedkFiIDP4+fCkWdx9aNDazq0MLGo4W8BWhX7vmXhsTAiciowGjjbGOOJQbkqCr/PzyfPTOPKzrdySZubmHj3ZHJ35dV0WErVWsYYRp85lvStGRTkFJCfXYDP4+Oz579mwTd/1nR4YWKR8BcCnUSknYg4gIuBacUvEJFewGuEkv2OGJRZa21YsZnFc5aRl51f/sVRPHze00x6+GO2rtlG2qadfPHSN9x67H14Pb4YR6qUAli7eD2Z23dhSrRJuPM8TJswo2aCKkWlm3SMMX4RGQ7MBKzAW8aYZSIyBkg1xkwDngYSgU9FBGCjMebsypZdm2Rsy+T+QWPZuHILNrsNn8fPlWOGcNHIiv8z/fPnOv6atQxPvrfomM/jZ+eWDOZ+Oo9TLzuhKkJXqk4ryHFjsUavO+ftyifgDzDtlZl8/dr3+Dx+ThpyHBfdfQ4JyfHVHGmM2vCNMd8A35Q49mCxr0+NRTm12UODn2bdkg0E/EE8hBL25Ic/oV33VvQe0KtC91i1cC0R1QzAnetm6S8rNeErVQU6p7THBCP/7pzxDk4cchyPXTyOhTMWFVXEPn32K3794ncm/PEUDqe9WmPVmbb7gf/WbeffwmRfnDvfw9Rx0yt8nyatGmGxWSOOO1x2DurQtNJxKqUiOeOc3PbqMJxxjqKavivBScvOB3PI0Z3Ckj2Az+Nj+8ad/DxlfrXHWq2jdFR02ek5WO1WKIg8l7k9q8L3STmtJ4n14/HkewgG9jw8rDYrp115cixCVUpF0e+SvrQ/rDXTX/ue9P8yOfasFE4eejw/TJoT9Xp3rpvFc5bR79K+1RqnJvz9QLvDWkd9JbQ7bRx7dkqF72O1WRk391Eev+R51vy5DhGhSavG3Pve/2jQtF4sQ1ZKldDusDbc+vJ1YccatWiI1Rr9rbt52+p/69aEvx9wuBzc9PxVjP/fW3gLvBgT+oWo1ziZ80acuVf3atamCS/++jiZO7Lwe/00btGQwo5ypVQ1SzmtJ/H14nDnuQkWq9RZbVZOv7r637o14e8nBl7Tj1ZdWjB13HTSt2Zw1BlHcM4tA0hqkBj1+oA/wD9/rsNmt9Hh8LYRSb2sGn3AH+DH93/mu0mzsdqsDLzmFE648FgsFu3SUXsn4A9gsVq0UlEKq83Kc3PG8OhFz7Fh2SbEItRvUo9R7/2PRgc1qPZ4xEQZ1bE/SElJMampqTUdxn7pj+8X8/jQ5wn4AhhjSKyfwJgv76Fjr3blftYYw/1njWXJnOW480Lz31wJTvoMPppRk26t6tBVLbFw5l+Mv+0ttv7zH3FJcZw3YhCXPXB+1OYLFbJzSzo+j5/m7ZpW6QNSRP4wxkRtC9Yq3QFm55Z0Hhr8NDkZueTnFFCQ6yZtczp3nfoInoLyJzD/NWspS+asKEr2EJog8stn81nz179VGbqqJZb9topHznuaLav/wxjIzy7g02emMXHkpBqJJz+ngDmf/Mb3k+eQuaPigxyqW+MWjTiofbMafRvShH+A+X7ynLAROLsF/AHmf/VHuZ9f9OPfuPPcEceD/iB//bQ0JjGq2m3ymE/xFHjDjnnyPXw98QcKcqMMNSvFxpVbeGPUe7xw00R+/3YRwWDk73V5Fs5YxJCDr+fZ61/lxVve4LK2N+13s1v3J9qGH8Xm1Vv55Jlp/LtkA51TOnDBHWdxUPtmUa9dMnc57z36KZtX/0fHXu244uGL6Hh4+U0r+ypjWxa+KMskBHxBdqVll/v5eo2TcbjseN3h97A5bCQ3SopZnKr22rhic9TjFquF9K2ZtOwcV+49Zr4zi5dueQO/L0DAH+CH93+m50mH8sjnd1W4WSgvO59HLngWT374m+3EuybT8+TutOmqq7CXpDX8ElYs+IebjrybmW/PYuXva/h64g/ccPhI1i5eH3adO9/D01ePZ+TJD7Pox6WkbUpn3rRURhz/AKsWrqmy+FL698CV6Io4LhboedKh5X7+lEuOR6J1zopw/HlHxyJEVcu179mWaK0SwaChcctG5X4+LyuPF295A0+Bl4A/ABSOS5+1lN++rHi/3fyv/sBiiQzE7/Pzw+To49/3xZpF/zLmome59tARPHHFS2wo5YF3IKgzCT/gD/DH94v5eep8dqWV3s734i2v487bM3Ep4A9QkOtmwoi3i67xeX3c3vcBvnt3NiU7vT35Hl6rwrbMlAGH0/mI9jjjnUXHXAlOTrjgWNoeumfR0rTN6Xw/eQ7zvkrF591Tm2/QrD6PfH4XiQ0SiE+OIy7JRf2m9Xhixmjik8qvmSl15cMX4Yhzhh1zxTs5/45BuOKdpXxqj8Wzl2OzR9bi3XkeZn/0S4Xj8BR4CURt3gyG9VFVxl+zljKi7/38MnUBG1dsYdaHvzD8qFGs/mNtTO5f3epEk87axesZdfpjeAvbHf0+P1c8fBFD7j437LpAIMDaReuj3mP5b6uLvv556gI2r95aanmr/1hX+aBLYbVaeeK7+5nx5k/88N5cbA4bZw7rz0lDjiu65u0HPuTTZ7/CZrMiIljtVp787gE6HdEegCP79+TTbW+w8vc1WKwWuvTuoKMrVIV1OqI9T8y8n1fvfJe1f62nXuNkhtxzDucOH1ihz9ud0dOOCGEVmfL0HnB41OZNCC0zEgsvDX8jbFmEYCD0MHnl9ncYN/fRmJRRnWp9wg8EAtw78HF2lei9nzxmCt2O7cJhfbsWHbNYLDjjHVFrB/HJe2q/f36/uMwaRINmVTur1e6wc9ZNp3PWTadHnPvzhyV89vzX+Nw+fOz5Yxh95v/x4ebXihK7zW6je59DqjROVXt173MIL88fu0+fPfyU7lHnfDjjnQy45pQK38dqs2CxCIEos9QXzviLi0aeE+VTFef3+dm0MnrFbtXCytfwg8EgK+b/Q352Pt2O7UxCvYRK37M8tb5JZ9mvq/BESc7eAg/TX/su7JiIcMb1p+KIc4Qdd8Y5OOeWPcm1UYuG2BzRa8Q2p42LR50b9Vx1+Hri91EfRu58D8t/W43f52fJ3OUsnrMsrKlHqepid9h59KtRhU2KcbgSnNiddi6482x6nNCt1M9tWLGZkac8zOn2IZyVdBkTRrwT8be6287NGZWO02qz4oyPfv+khtEnRFbUhuWbuKztzdw78DEeu3gcFx08rFpGF9X6Gn5BTgFE6WAyBnJ3RW4ycu3YS9m5JYP5X6Vid4ZGs/S94Bguvf+ComsGXtuPqeOm4/cGIj5/yajBnHFdza0GnZ8bOeQSQg+z5fNX89Dgp4o6yiwWC/d/fDtH9u9ZnSGqOiBtczrTJszg3783csjRnTjrxtOo1zi56Hz3Pofw8dbXWfD1nxTkFHBE/x40bdW41PtlbMvktuNGk5+djzGh9v7fvvw9YoVZCCXqXv26V/pnEBHOvul0vhw/I2wYqjPeyQW3D9rn+wYCAe45/TEytmaErWY+8e7JdE7pwCFHdapM2GWq9Qm/+/GH4PdFJmZXgpOTLjou4rjDaeeBj+8gbXM6W9dso2WXgyOmQDdv25SHpozkictfwuf1EQwEadC0Pg99NrJKh2RWxMlD+rD05xURtXy/L8B7Yz6NOP7w4KeZ/O94nPFOvnrlO36eOp/EevGcfcsAjj2r4gu3KbXb6j/WMvKUh/F5/Pi9fhb9+DefvfA1439/goPa7Rne7Ip3cuKFx1bonl+9+h1ety8sQfo8fqw2C444R1H/nNVmJT45jqH3nheTn+Xqx4eSlZ7DrA9/weaw4ff6OfP6fpx/x74n/GW/rip6cBXnLfDx1SvfacKvjIR6Cdw07ipevf0dfB4fwaDBleCkQ8+2nHRxZMLfrUnLRjQpY4hZ7wG9+GTb6/y7ZCOOOAetuhwcMYNuw/JN7ErLptMR7attBMwplxzPzLdnsfrPdbhz3VhtFmx2GyddfBxzPp4Xcb0xhh8mzWXmu7PYunZ70R/O0l9XMvi2M7jmsUuqJW5Ve4wb9hoFOXveNL1uH36vn4kjJ/PQ1JH7dM9//vw3agetM97JObcMYPm81ezckk6vfocx9N7zyvzb3Rs2u42Rb97MsKcuZ/uGNA5q34zE+pVra8/dlRd1tq0xhqyd5c+lqYxan/ABBg3rT5eUDnw98QeyM3I4/tyj6HHSoWxYtpmDOzYvMxlv35BG5vZdtDm0FXEJ4ePfrVZr1PVrdm7N4P5BY9m8emtou0Kvn2seH8r5I/a9VlBRNruNp354kN+mpfLbtIXUa5TEwOv6MW9aKj6vP+J6r9vHkrnL2fbvjqJkD6FX5inPTufc4QNp2Lz6F3lSByZPgYd1SzZEHA8GDanfL97n+3Y+sj2LflgSMWEw4AvQ79K+XPN4bComOzbt5NOnp7Fk7nIO6tCMIXefS9ejO5HcKClmExO79zkk6t+iK8HJ8ecdE5MySlMnEj6EhpKNeHUYXreXp64ezzPXvoLdaSPgC3DByLO48uEhYU/d7IwcHjn/GVYu+Aebw0bAH+SqMUO44I6zyi3rwbOf4N+/NxIM7Nmu8O37P6Jd99YccWqPKvsZd7ParPQ972j6FptI5c7z8N6jU4ra73dzxjvIycyN2tFrd9pY9tvqsPsoVRab3YbFaom6/EdFxuiXZtAN/UOjzzx7mnUcLjuHHn8Ibbq1KvvDFfTfuu3cnHIP7jw3fl+Af//eQOrMv7hn0v9i+jeQ3CiJqx+9mHcf+gRvgQdjQm8qrQ5pwSmXHB+zcqKp9aN0Snr51jdDtV2Pj/zsAjwFXqY+O53v3pkddt1jQ8ax/LdVeN2F1+V7ePfBj1nwddnr1WxevZWNK7dE/MJ78j1Mfb7i2xXGWpeUDvQZfBSuhPAJW70H9KLNoa2ibsJckOvm/cem8MvnCyImmCkVjdVm5YQLjo0Ya++Ic3DmsH0fzNCweQNe+O1xep7cHYvVgivBxcDr+jHmi7srG3KRdx78iPzs/KI+P2PAk+/lpVte36d1fspy4Z1nM/bb0Zw4pA9HntaTm5+/mud/frTK97iNyfLIIjIAeAGwAm8YY54ocd4JTAKOBNKBIcaY9WXdsyqWR/a6vZzb4KqobYEtuxzM2yteAEJNMld0HI7PHXldz5MO5ZmfHi61jOXzVnHvwMfJz45cRKrTEe2ZkPrkvv8AlRQMBvnlswXMeHsWGMNpV57ECRcey4Zlm7j1mPsiFsTazZXgZPD/zojZa7Oq3fKy8xl95ljWLPoXq82C3+sn5fTDuf/j27E7qnfT7r0x5ODrydi2K+K4I87B2ytfKHMU0f6krOWRK92kIyJWYDzQH9gMLBSRacaY5cUuuxbINMZ0FJGLgSeBIZUte2/l55S+kl9WsYXHsnfmYLNboyb89P8yyyyjfc+2UV9n7S77Xm1XWBUsFgsnXHAsJ1wQPjKi3WFtuOONG3n+xon4fYGIn9ud52HKuOkMvu1M3SpRFdmVlsWUZ7/i928X0ejgBlxwx1kc2b8nCcnxPP/zo6xbsoEt//xHu8Na07LzwTUdbrnqNUmOmvBN0JBQL74GIoq9WDTpHAWsMcasM8Z4gY+AklPczgHeLfx6CtBPamBR6HqNk6nXOLLjRUTofvyeWactuxyMRBm8b7Nb6T3g8DLLcMU7ueHZK8MmbDhcdho0rce5t1Zs6nlNOGVoX6Zsf5MOPdtGPW932Fgxf3XUc6ru2ZWWxbCeI/ns+a/59++NpM5czEODn+aLl78tuqZ9jzb0Pf+YAyLZA1w48uywJk8Au9POceekkJC89wnf6/Ex66NfmTzmU37+bAF+X2RHbXWLRcJvAWwq9v3mwmNRrzHG+IEsIGLclIgME5FUEUlNS0uLQWgR92f4S9eGJWOL1YIr0cm1Yy8tOuZw2rlxXHjStjlsJNZPiFh/J5pBw/oz9tv76TP4KLoe04lLRp/Ha389U+p2hfsLh8tBu8NaR23PN0FDg2b1ayAqtT+a8txX5Gbkho028eR7ePPe93Hnx2bhsup26mUncP4dg3C47MQnx+Fw2enVrzt3vnHTXt8rbXM6V3YazrhhrzLpkU94+uqXua77HWSn51RB5BVX6TZ8EbkAGGCMua7w+8uBo40xw4tds7Twms2F368tvGZnafetyi0Ol89bxYdjP2fLmm10O7YzQ+8dTIuOB0Vct3j2Mj55Zho7N6dz5Gk9uPDOs2t90lu7eD239RkdtmCUxWrh4A7NeGvFC7p3qQLghl4jWbc4cvhlfHIcT8x8gK5Hh08eCgaDZKfnEJ8cX+Udk5WVl5XHxpVbadyi4T6P5x896P9Inbk4rHnXZrdyyiV9uevtW2IValRV2oYPbAGKj4tqWXgs2jWbRcQG1CPUeVsjuh3bhUenjSr3up4nHVqhNeZrkw4923LXW7cw7obXMEFDwB+gZZeDGfPF3ZrsVZFGBzeImvD9vgD1myaHHZvz6Twm3PYWOZm5iAinX3MKNz135X7bgZtQLyHigbU3AoEAf3y3OKIvz+8L8PPU+VWe8MsSi4S/EOgkIu0IJfaLgZLDOaYBVwLzgAuAn4yO86uQrJ3Z/Pr573jdPo4+84hSd96KpRMvOo7jzu3Nv39vJD45npadIt9+VN124Z1ns2TOirDdpmx2K52OaB+2fMJfs5by9NUvh70xfvf2LHxu3z41lajKqXQbfmGb/HBgJrAC+MQYs0xExojI2YWXvQk0EpE1wB1A+dVrxa9f/M6lbW7ilTve4fV7JnNd99uZ9Mgn1VK23WGn85EdNNmrqHqdchjDnr4cV4KzqL37kKM78cjnd4Vd9/5jU8OSPYQ2Lvnx/Z/Jy8qrzpCrjdVqJeX0wyP6wmx2K30vOKZG57TEZBx+VajKNvxYCfgDfDj2M754eQb52QV0O64zN4+7mvY92lT63nlZeQxpMSzij8UZ7+DZWY/QpXfHCsX30ZNf8OXL35KfU0CPEw7lxueupPUhJfvUldo3ngIP65duol6TZJq3bRpx/rJ2N7N9Q+QAjLhEF+MXPkGrLrXzd3HnlnT+d9xocnfl4c7z4IxzICJFc4COOSuF4S9dG7EwYyyU1YZf52baxtJzw17loye/ICstG5/Hx+JZyxhx/P389+/2St97wTeLoo6W8bp9/PDe3Ard49nrXuHDsZ+RuT0LT76X1JmLuPWYe9mxqdS+cqX2ijPOSZfeHaMme4AuR3VEouw7a4BmbZpUcXQ1p3GLRrz7z0vc+cbNXP7AhcQlukKLyPkC+H0B5k1byP+Ova/a96TQhL+PMrZlMvujXyNq4F6PjynPfrXP983LyuO5Ya/yzDUTwlYcLGJM1OWeS9q5NYPZH/8WFp8xodnGn9XgEg+qbrnioQtxxjnDNj13JTi5dPR5OFzRNxepLewOOydeeCzterTGne8JW8cq4A+Sk5HLb18srNaYNOHvo02rtmKPMrws4AuwauGafbqnMYaR/R7h+0lzSt2r0xnvDNu/tjQbl2/G4YqMz+8NsGLBvsWn1N5q060VL/z6GL0H9iKxQQKtu7bgtleGVWg+S22xccWWqLvuFeS62bii5IDGqlVnVsuMni9TdwAAEONJREFUtYM7NI+alC1WC+0O27c2/CVzl7Nl9X/4oyydCqFk3++yE8rcBm63gzo0ixqf1WahXffYrC6oVEW079GGx6ffV+Y1Ozbt5M/vlxCXFMfRZx5RqZU1K8MYw8YVm8ndlU/HXm1xxlU+jjbdWuJMcEa8scclumjdtXr7MDTh76MmLRtx9KAjWfD1n2HryDucdi666+wyPlm6jcs3E4iyDg9Ax17t+N+E6ys8Pvigds044tQe/FliDXG7w16hJZ6Vqi6THvmEj5/8AovVUtjeLzw+/V4O69u1WuPYtn4H9w8ay/b1aVhsFoJBw//GX8cxg47kx/d/ZuvabXQ7pjN9Bh+1V3MIjhl0JPWb1MNb4Ctq1rHarCQ3SuK4c3tX1Y8TVa0bpRMMBsncnkVi/fiYPJ3L8v/tnXt8U1W2x78rSZu+5T3K8KgiRRAVHEAEfICjAtcBfKGMICgoiE/8+HYcEcWroF4FK8oAIiiCOoJ4gRmEwshDQRCUKiMFxJGnlUopNE3aZt8/zqE3bZI2TZpHm/39fPLpyTn77PPL6cnKOWuvvZbLWcrfHpnPitk5uBwuzrqgLfdlj6HTxR2C6m9bzg6eHjIFR5W6tEmpdu6cMoI/3XW1nz1943Q4eWPCXFbN+xdlpeW07dSK+2fcybm9gtOn0dQ1O9bt5PEBkyvF8wOknpbCB4dnRWxWrlKKUR3u4/DeI7jd/28TE5Js2Gw2o7aFw0VyWhLNWzdl2sbJpJ4WeOWrY/mFvHH/26xfvBlQXDyoO/dMuz0sM/eri9JpUAY/5/11vPHAXKNwOUZujLunjw7LRVNeXk7uun9T9NsJzu19DhlN0rDarCH16Xa7Gdf1YX7+4WCFW8diEdKbpPPO7ulBJXA6pbW8tLzBD5Jp6h9Tb8vms3lrveq7pmQk8+T7E+gxoGtEdOzclMejV07yutnyRYLdxqC7+zPupZERUFZ74iIs8+vVO3jljjcpzD+Oq6QUV0kpq99bx6tj36rzY/20cz+3ZI7nqcEvMvW2bIZn3sUHUz8JuV+LxcJLayZy6Q0XY0s0KgddeOX5TN/0fNDGHoyJINrYa2IRZ4nLy9gDYEaURYrC/ONYfISP+qLUWca/Fm0Ms6Lw0GAM/oLJvmf0rV20kRPH6m5Gn9vt5okBkyk4WICjyEHxcQeuklIWPP8x23J21Lo/pRS563eyeNpyvvh0C6kZKTz+7n0sdyzgH66F/PeKv1Saqq7RNCQuH9rLKyUxQFlZOV37dY6Yjo492/usM+uPUJ/mo0WDGbT1N9nJlmCl4PCxkCvNn+KHr/ZQVHDC666k5KSTT2espGu/8wLuy+lw8uhVz7Jn+z7Ky9zYEq2kN07j1fXPBZ2lzx+OEw4O//gLzVs3q7NzodGESq/B3el6xXlsy8ml5EQJVpsVW4KVe14fXSsfeaikZCTTqkPLSgnhLDYLNpuVMldZJb9+YlIC/W/vW/G+vKyczSu2cWjvEdp1yeT8SzvFbKLBBmPwO/XM4tefj1b6x5zi9My6m9HnKHL4nDkIUPTbiVr19d5zfydv696KKJpSZynOYhdTRk5n6uqJoUoFjCeI2U8sYPG05UYVL2cZV428jHtfH1Nv71I0DQeLxcLEjx9m62ffsnHJZlJPS+GqUX0jnv5j5sPzObDrUKV1gnDDQ39i5dtrOXncQZmrDKvNQofuZzPUnEfw64GjPNDnKY4XFFHmKsOWYKPtua2ZsuqvJKcmRfQzBEKDMfgjnh7KpmVfU3LSWZGcyJ5iZ8TTN9ap/7pjz/aU+5jpak+xe5UOBOPXf9Pyr9mzbR+nn9mCS27oWRFj/M+5ayuFTAK4y93krv83xUUOUtKTQ9a7ZPpylkxfgcvhwmVWeFw1/3PSGqUy5oXhxjHdbrbn5LJ9bS6NWzSi77DeNGquSxlqIoPFYqH71V3ofnX11eTCRXlZOStmrfaq6VxeVs7qd9cxf282m5dv48hP+XTo3o6OPbMq7uCn3vYG+fuPVqRCLnWWsWf7PuZN/ICxU2+N+GepiQYVpbPvu5+Z8+QCvt/4A03OaMyfn7iOy2/qXefaVsxeTfb9cygtKcXtViSl2mndoSWvrn+u0o/LycKTPHDJUxzZl4/jRAnJaUnYkxN5beNkWrY7nRt/N5pjHrV0T2FNsPLRkdl14noZ1nosvx4o8FqflGrnk8J5uMvdPPFfz7PzizxKTpaQmJyIxWJh8rLHA5rgpdFEEqUUOQvWs3jaMk4WFtN7SA+GPjKYjCbepUsDpbjIwXVNR1Fe5j0HJiktiU+Pz/e5X0mxkyGNR/q8AWzU4jQ+PDwraE2hEO4CKDFD5rmtmbTk0bAfZ8DoKzi765l8+uZKCn85Tq8h3ek7rI9X+Ofcvy7iQN4hSp3GYJDjRAklxU6mjsrmf9Y9yyU39GTF7JxKM2tFjJmJdeVnP37Ut5vJ6XBx/GgRi15cwncbfqiYPHbq77M3vcLC/W9htWq3jyZ2mDFhLitmr6bETFXw8WvLWbtoIzO/fTnoJ+LktCSat2rG4X2/eG3r1DPL737K7TaywPnAM29OLNFgonQiTfsLz+LBmeN4ZskjXD2qr89Y/7ULN1QY+1Mot2Ln5jyKixyMevZmWrRpRlKa4euzp9hJbZTKI3Pv8eorWLK6neVzfXrjNG5pO56/v7as0kzhUzhPOn1WNNJoosWvB47yv299VmHswRj3OpZfyD/fzgm6XxHh3uwxZgpjY51R6zqJO6eO8LtfcloyWd3aeQ3Q2hKsPt27sYA2+OGkmpF6Echoks7fdrzChLfGcu39A7ljynDe3ZtN5rl1l+tm3MsjSUqxVww0ixgTRxwnSnCVuFDlvm9RFPgdnNZoosGuLXtJsHs7JZzFLras/CakvnsM6MrUnIn0vKYbrbJa0ndYH7I3v0C7CzKr3e+hOeNJa5yK3RyXM2biNuP2ycNC0hMuGpRLJ9bo9+c+fDpjZaUkZhaL0OniLJLTjMfPRHsC/Yb1od+wPmHR0KH72Uz78nnee+4j8rbupU3HVhw9WEDe1z9Wu19ao5QaL3aNJpI0OaORzyg8i9XiNx9/beh4UXsmfVI7l3Cbc37P/L3ZrHl/A/vzDpL1h3b0ue6imC3Urg1+GBn5zE1sX5PLoT1HcDpc2FMSSU5NingR4zM7t+EvCx+seD+m8wS/be0pidgSbEz8WBct18QWHbqfTYvWzdi/62ClAuEJdhuDxtcuz1RdkpqRwjVjr4za8WtDgzP4SikjpnfpV0ZM762XRa2MWkp6MjO2TmHrym/YbYZl9r62R9R//XsMvJCDuw97zSxMsNu4e9rtXD60V8UTiEYTK4gIL372FJNufJnd237EarViT07koTnjadtJp/wOhJDCMkWkCbAIyAT2AUOVUr9VadMFmAFkAOXAZKXUopr6DiYs0+1288z1L/H1qh2UnDRm7VkTrNyXPYarR/WtuYM44Vh+IWO7PExRQRGlzjJEIDHZzr2vj9bnSVMvyN9/lOIiB62yztCRZFUIW7ZMEZkCFCilXhCRx4DGSqlHq7TJApRSKk9EWgJbgY5KqWPV9R2Mwd+wZDMvjJhWaRQfIDE5kQ8OzozoVO1Y5/jRIhZPX85XK7bTvHVTrp9wDZ17nxNtWRqNJkTCGYc/GLjcXH4HWAtUMvhKqV0eywdF5BegOVCtwQ+GNQs3eBl7MMKktuXk0ufai+r6kPWWjKbpjJx4EyMn3hRtKRqNJkKEGpb5O6XUqQQUh4Fq0zqKSA8gEdjjZ/udIrJFRLbk5+fXWoxnHG1VdHpgjUYT79Ro8EVklYjk+ngN9mynDN+QX/+QiJwBzAduU0r5rOOnlJqplOqmlOrWvHntE571v71fRTxslWPTJYKpVjUajSYWqdGlo5T6o79tInJERM5QSh0yDbr33GSjXQawDHhSKfVl0Gpr4LxLOnL9g9fw4dSliMWCxWrc7k/65NGoR8ZoNBpNtAnVh78UGAm8YP71KvskIonAYmCeUuqjEI9XI6OeuZmBo69gy8pvSUlP4qJr/hCTaUo1Go0m0oQapdMU+ABoA/yEEZZZICLdgHFKqTEiMhx4G/jOY9dRSqnt1fUdbBFzjUajiWfipoi5RqPRxDtxUcRco9FoNNWjDb5Go9HECdrgazQaTZygDb5Go9HECTE7aCsi+RiRP7WhGfBrGOSEC603/NQ3zfVNL9Q/zQ1db1ullM+ZqzFr8INBRLb4G52ORbTe8FPfNNc3vVD/NMezXu3S0Wg0mjhBG3yNRqOJExqawZ8ZbQG1ROsNP/VNc33TC/VPc9zqbVA+fI1Go9H4p6Hd4Ws0Go3GD9rgazQaTZxQbw2+iDQRkc9EJM/829hHmy4i8oWIfCci34pIVOr5iUh/EflBRHabtX+rbreLyCJz+yYRyYy8ykp6atL7oIh8b57T1SLSNho6PfRUq9ej3fUiosxsrlElEM0iMtQ8z9+JyIJIa6yipaZroo2IrBGRbeZ1MTAaOj30zBGRX0Qk1892EZFp5uf5VkQujLTGKnpq0nuLqXOHiGwUkQuCOpBSql6+gCnAY+byY8CLPtpkAe3N5ZbAIaBRhHVaMUo6noVR3vEboFOVNuOBN83lm4FFUTyvgejtC6SYy3fFul6zXTrwOfAl0C1aemtxjtsD24DG5vsWMa53JnCXudwJ2Bflc3wpcCGQ62f7QGAFIEBPYFOM6+3lcS0MCFZvvb3Dxyig/o65/A4wpGoDpdQupVSeuXwQoyJX7WsnhkYPYLdSaq9SygUsxNDuiedn+Qi4QsRfdd6wU6NepdQapVSx+fZLoFWENXoSyPkFeBZ4ESiJpDg/BKL5DiBbKfUbgFLKZzW5CBGIXgVkmMunAQcjqM8LpdTnQEE1TQZjFGVSyqjC18is2hcVatKrlNp46loghO9cfTb4dVpAPYz8HvjZ4/1+c53PNkqpMqAQaBoRdd4EoteT0Rh3StGiRr3m43prpdSySAqrhkDOcRaQJSIbRORLEekfMXXeBKJ3IjBcRPYDy4F7IyMtaGp7nccSQX/nQi1xGFZEZBVwuo9NT3q+UUopEQmkgPpI5aeAuqb2mNXMugGXRVuLP0TEArwCjIqylNpiw3DrXI5xN/e5iJynlDoWVVX+GQbMVUq9LCIXA/NFpLP+vtUtItIXw+D3CWb/mDb4qh4VUK+GA0Brj/etzHW+2uwXERvGI/HRyMjzIhC9iMgfMX54L1NKOSOkzRc16U0HOgNrTS/Z6cBSERmklIpWSbVAzvF+DD9tKfCjiOzC+AH4KjISKxGI3tFAfwCl1BcikoSR9CuarqjqCOg6jyVE5HxgFjBAKRWUfajPLp1TBdQhRgqo++EroL2InGnquRlDuyeen+UGIEeZozNRoEa9ItIVeAsYFGXfMtSgVylVqJRqppTKVEplYvg/o2nsIbBrYgnG3T0i0gzDxbM3kiI9CETvf4ArAESkI5AE5EdUZe1YCtxqRuv0BAo9XMQxh4i0AT4GRiildgXdUTRHpkMc1W4KrAbygFVAE3N9N2CWuTwcKAW2e7y6REHrQGAXxvjBk+a6SRiGB4wvx4fAbmAzcFaUz21NelcBRzzO6dJY1lul7VqiHKUT4DkWDFfU98AO4OYY19sJ2IARwbMduCrKet/HiMorxXhaGg2MA8Z5nN9s8/PsiPY1EYDeWcBvHt+5LcEcR6dW0Gg0mjihPrt0NBqNRlMLtMHXaDSaOEEbfI1Go4kTtMHXaDSaOEEbfI1Go4kTtMHXaDSaOEEbfI1Go4kT/g/1k58H9+jOwQAAAABJRU5ErkJggg==\n","text/plain":["<Figure size 432x288 with 1 Axes>"]},"metadata":{"tags":[],"needs_background":"light"}}]},{"cell_type":"markdown","metadata":{"id":"ysWXHvng2ohM"},"source":["If we run the M-P Neuron, the accuracy decreases"]},{"cell_type":"code","metadata":{"id":"HIwrR0kS2uZZ","colab":{"base_uri":"https://localhost:8080/","height":35},"executionInfo":{"status":"ok","timestamp":1590664205402,"user_tz":-120,"elapsed":432,"user":{"displayName":"Alessandro TORCINOVICH","photoUrl":"https://lh3.googleusercontent.com/a-/AOh14Gi96E7HK6ff0uWSudqbJvEMactRTPtsT5-4448y=s64","userId":"03260776184459049943"}},"outputId":"c7dbda8f-1f5f-4ec5-8f55-68d3de6c2c84"},"source":["y_pred = mpn(Xp)\n","accuracy = evaluate(y_true, y_pred)\n","print(f'The accuracy with theta = {theta} is {round(accuracy, 2)}%')"],"execution_count":null,"outputs":[{"output_type":"stream","text":["The accuracy with theta = 1.0 is 80.0%\n"],"name":"stdout"}]},{"cell_type":"markdown","metadata":{"id":"0hk9Npx43C4D"},"source":["The neuron must be improved by introducing some learnable parameters, and a learning algorithm. First of all, the forward step changes in the following way:\n","1. Take an input $\\vec{x}$\n","2. Compute $g(\\vec{x}) = w_0 + \\vec{w}^\\top\\vec{x} = \\sum_{i=0}^n w_i x_i$, with $x_0 = 1$\n","3. Compute the thresholding function: if $g(\\vec{x}) \\ge 0$ then $f(\\vec{x}) = 1$ otherwise $f(\\vec{x}) = 0$\n","\n","The parameters to learn are $\\vec{w} = \\begin{pmatrix}w_1 & w_2 & \\dots & w_m\\end{pmatrix}^\\top$ and $w_0 = -\\theta$, the bias, that we were manually setting before. In our case $n = 2$, so only $3$ parameters need to be learned.\n","\n","This model is called Perceptron and have been theorized by Rosendblatt in the 1958\n","\n","\n","\n"]},{"cell_type":"code","metadata":{"id":"AMWNtDGO-Nr8"},"source":["class Perceptron(nn.Module):\n"," def __init__(self):\n"," super().__init__()\n"," w = torch.zeros(3)\n","\n"," # special wrapper for learnable parameters, by default it requires the grad\n"," # but in our case we don't use it\n"," self.w = nn.Parameter(w, requires_grad=False) \n","\n"," def forward(self, x):\n"," g_x = x @ self.w\n"," f_x = (g_x >= 0).to(torch.float)\n"," return f_x"],"execution_count":null,"outputs":[]},{"cell_type":"markdown","metadata":{"id":"xQCNUZtuBE_Y"},"source":["Now, we need an algorithm that allow us to learn the weights. In this case, the **delta-rule** is used. The procedure is quite simple:\n","\n","1. $e = 0$\n","2. while $e < \\mathcal{E}$\n"," 1. for $\\vec{x}_i \\in \\vec{X}$\n"," 1. $\\hat{y}_i = f(\\vec{x}_i)$\n"," 2. for $j \\in \\{0, \\dots, m\\}$\n"," 1. $w_j^{(e + 1)} = w_j^{(e)} + \\eta(y_i - \\hat{y}_i)x_{ij}$\n"," 2. $e = e + 1$\n","\n","\n","$\\vec{\\eta}$ is the **learning rate** (lr) and is set manually. There is not a precise rule to set it: if the lr is too low it will slow down the convergence, if it is too high the algorithm might not converge.\n","\n","A complete iteration over all the dataset is called **epoch** (for big datasets it takes a lot 😅). We can decide to repeat the algorithm for a fixed number of epochs $\\mathcal{E}$ in such a way to improve the final result"]},{"cell_type":"code","metadata":{"id":"Ksp8LayiF4KP"},"source":["def delta_rule(X, y_true, p, epochs=1, eta=0.5, device='cpu'):\n"," X, y_true = X.to(device), y_true.to(device)\n"," for e in range(1, epochs + 1):\n"," for x, y in zip(X, y_true):\n"," y_hat = p(x)\n"," for param in p.parameters():\n"," param += eta * (y - y_hat) * x \n","\n"," print(f'\\rACC: {evaluate(y_true, p(X))}', end='')\n","\n","def pad1(X):\n"," \"\"\" Pad the dataset with ones on the left\"\"\"\n"," return torch.cat((torch.ones(len(X), 1), X), dim=1)"],"execution_count":null,"outputs":[]},{"cell_type":"code","metadata":{"id":"IQ6OoV1FNxYM","colab":{"base_uri":"https://localhost:8080/","height":35},"executionInfo":{"status":"ok","timestamp":1590664619923,"user_tz":-120,"elapsed":9240,"user":{"displayName":"Alessandro TORCINOVICH","photoUrl":"https://lh3.googleusercontent.com/a-/AOh14Gi96E7HK6ff0uWSudqbJvEMactRTPtsT5-4448y=s64","userId":"03260776184459049943"}},"outputId":"d33e8d4e-14a8-4507-fbe9-638a199d33f7"},"source":["p = Perceptron().to(device)\n","delta_rule(pad1(Xp), y_true, p, epochs=1, eta=0.05, device=device)"],"execution_count":null,"outputs":[{"output_type":"stream","text":["\rACC: 100.0"],"name":"stdout"}]},{"cell_type":"code","metadata":{"id":"U-Lxr9yt1r34","colab":{"base_uri":"https://localhost:8080/","height":265},"executionInfo":{"status":"ok","timestamp":1590664871622,"user_tz":-120,"elapsed":874,"user":{"displayName":"Alessandro TORCINOVICH","photoUrl":"https://lh3.googleusercontent.com/a-/AOh14Gi96E7HK6ff0uWSudqbJvEMactRTPtsT5-4448y=s64","userId":"03260776184459049943"}},"outputId":"0c67b51a-34ae-4212-e22a-eb318bdde915"},"source":["# plotting the decision boundary\n","def plot_decision_boundary(X, y, w, low, high):\n"," m, q = -w[1] / w[2], -w[0] / w[2]\n"," px = torch.tensor([-1e-1, 1.1])\n"," py = m * px + q\n"," plt.scatter(X[:, 0], X[:, 1], c=y)\n"," plt.plot(px, py)\n"," plt.show()\n","\n","plot_decision_boundary(Xp, y_true, p.w.to('cpu'), a, b)"],"execution_count":null,"outputs":[{"output_type":"display_data","data":{"image/png":"iVBORw0KGgoAAAANSUhEUgAAAXwAAAD4CAYAAADvsV2wAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nOzdd3wURRvA8d9cz6XRAii9C1IEg1JEEURBkaIIomJFbKioqCCoiPqCFQVBxYZgFyyAFAFpSpFQpUtvAiEJadfv5v3jQsjlNoXkcoFkvp/P+zHZ3dt5wps8uzs784yQUqIoiqKUfbrSDkBRFEUJD5XwFUVRygmV8BVFUcoJlfAVRVHKCZXwFUVRyglDaQeQlypVqsi6deuWdhiKoigXlPXr15+SUsZp7TtvE37dunVJSEgo7TAURVEuKEKIg3ntU106iqIo5YRK+IqiKOWESviKoijlhEr4iqIo5YRK+IqinPek9xTStQ7pPV7aoVzQQpLwhRCfCyFOCiG25rH/TiHEFiHEP0KIVUKIVqFoV1GUsk1KL77UF5CJnZEpDyMTu+FLeRwpnaUdWhAp3UhvIlK6SzuUPIXqDn8a0D2f/fuBa6SULYBXgakhalcpgM/nY/WcBN5+YApThn3O3s0H8j3e4/bgcrjCE5yiFEBmTgX7XMAFMh1wgnMZMu2NczuPlEjXJmTmZ0j7bKS0hy5GKfFlTEGevAKZ2AV58gp8GR9zPlYiFqEKSghRF5grpWxewHEVga1Syhr5HRcfHy/VOPzi8Xq9vNT7Tbas2I4jw4FOr8NoMjDk7bvp9cgNAcemnkrjvYemsnpuAtInadK2Ic98+jB1mtUqpegVBXwnO4DvlMYeM6LaZoQo+J5VSjcy5VFw/Q24QZgAI6LSVwhjk+LHmDkN0icAOS8iERD9LMJyPTLzM3CtBv3FiMgHEabLi91mfoQQ66WU8Vr7SqMP/wFgvtYOIcQQIUSCECIhMTExzGGd/2zpdjJTMwt9/OrZCWxZvg1HhgMAn9eH0+7i42e+JC05Pfs4KSXPXDuGNXMT8Lq9+Lw+dq7dzbCrXiQtKT2v0ytKyfPl9fvnBjyFOoW0fQ+utfgTsgekDWQq8vTQ0NyFZ35MYLLH/33mB8hTPcH2FXh2gvMPZPJ9+Gy/Fr/NIgprwhdCXIs/4T+vtV9KOVVKGS+ljI+L05wZXC6dPJTI8C5juLXKffSr+gBDrxzJoZ1HC/zc8h9X48gM7us0GA1sXHL2dcuWFds5eTARj9ubvU1KcDvdLPhiaWh+CEUpClMb7e2GhghhKtw57D8CjuDt3hPgzXNSaqFIKcGXpL3TlwIyA//F6QwHpL+GlIW7WIVa2BK+EKIl8CnQW0qZx7+QkpvH7eHJq17kn5U78Li9eNxedifsYdhVo8lMs+X72YgoC0IngncIsESas789tuc4Pl/wnY7T7uLQ9sPF/hmU8klKN76Mz/AlXo/vZGd86W8i87xj1yaiXwBh5WwVGD0QgYh55RzO4s1ju8hnX+EIIUBfL4+9erSfQtzgPVSsdosqLAlfCFEb+AkYJKXcHY42y4q1v20gMzUTn9eXve3M3fey7/7K97M9HuiKyWIM2q7T6WjdtUX29/Vb1kFoXBcskWaatG1Y9OCVck2efhwy3gfvAfAdg8wvkUn9kLLwgwKEsQmi8hyIGACGFhDRB1Fl1rn1g1v6Apbg7boKoK9f+PPkFWPMSI3zW0Cfx/sv6fG3XQpCNSzzW2A10EQIcUQI8YAQ4mEhxMNZh7wEVAamCCE2CSHU29hCOr7/JG5n8F2CI9PJ0T35j0luemUjBr10G0aLkYgoC9boCCJjrbw2dyQm89kLQeP4BjSOb4Axx8VBb9BhjbFy3aCrQ/fDKOWGdG8H5yoCu1Lc4DsBDs1XeHkShlroYl9GV2UWuthxCMO53YSIyLvA2CzrSQHAAiISUWGi/w69mIS5M6Lix2C8DEQFMLZGVPwEEf00EJHraBOYOiB0lQK2SimRsnhPG4URkmqZUsqBBewfDAwORVvlTcPW9TCYDHhcgUk/IspCk/gGBX5+wHN96Hb3NWxcshVLpJm23S/DZAns+xRC8L95L/Dlyz+wcNpSPE4P7W6+nAffHEREVO5fWEUpBPcW7e3ShnQlICJ6h6wp6UtGZkwF52IQ0YjIu8HSJzuZC2GGSt+A60+kax1CVw0ieiJCeJctzO0R5vbBsUXth4wpIAwg3WBsDRE9kbZv/V8b6iLTxoN9FuBCGpojYscijJeGLLaAOM/HsaKghmWeIaXkyY6j2LvpAC6H/+WPwWSget2qTN3yNkZTcJdNKLmcbhZ9uYyVs9YQVSGSmx+5gVadS+aXUSk7pHM58vQwkLlHlZkhaii6qIdC044vA3nqpqyhm2dejkaAtR+6mBdD0kZxSV8GePYipQ1OPwU44czdvIgCmQbk6OYSVkSV3xD6fEeu5ym/YZkq4YfA9jW7+fLl7zmw9TC1L6nBPa/0p/lVTUN2fnumg69fm8mi6cvxeXxc3b8D944dQHTFqJC1ocXtcvNUpxc5uP1I9mgfs9XMnaNvZeCIviXatnJhk9KDTOzq78Lh7PsnfzJbjNBXyfuzvtNgn4v0nUAY24D5aoTQax7ry/jM/54gaBSOGRG3GKGvdva83uPg/BOEBcydEbqS/fvJSUqJPNUDvPuBgnKuEax3oot5oUhtlduEf+JgIpuWbiWqQiRte7QO6LcOlc3LtjHqpv/htJ+9QpsjTLz807O0veGykLcXToumL2fiY58EDe00WYx8c+gjYqvElFJkyoVAeo8iTz8F7u2AAH11ROzbCFPelVWkazMy5d6sO2AHYAVjY0Sl6QgR/OLVlzwYXCuCTySiELFvISxd/cdlTIWMSSB0+F9dSkSFKQhzhxD8pAWTnoPIUzejOTxUi7EdusrTi9RWfgn/vF3xqjiklHw68mt+mTgPnV6HTifQG/SM//1FGl9ecL/3ufjw6WkByR78wxmnDPuCL3a8H9K2wu3PX9Zqj+M3GdiyYgedbrmyFKJSLhRCXwNR+QekNwlwga56vi9JpZQa3UA2cO9EZk5HRA0J/pC+Jv7hj7lfePpAX9V/Xvc/kPEB/q6UHO2dfhSqrkaI0L6n8t9EexEiZ3p1+y82hbq/NoGpRcGHFUGZrJaZ8PtmZk9egMvhxpHpxJbuID0lk1E3jcPrDe2b8ANbtcfTHtl1DJ/Pp7nvfJaWnM6auevZtmoXMZWj0WmM45cSoitGlkJ0yoVI6Csj9BcVPCLGexB8yRo7HGD/RfvckXcBuZ/c9aCvAQZ/lRdp+4mAPvJsOnBqPB0UkZQ+fw2dk22RJy7Fl9gV6fgjK6T6ILT+ZnT+eLMJECaEdVDI4sqpTN7hz/tkkeadqcvuYsfq3SHtX4+NiyX5v5Sg7dGVotDpLqzr6fdv/sL0MT9gNBnwSUlEpAWDyZD9sviMiCgLLa4O3b+hovj5u1o05dGHLwwNocL7yLQXQNr9Y9yNLXINuXQQ8B7hDCnhHOYEFERmTILMz8kus+A97H9iqfixfwRPhQnIlAezuqtc/mGi+rpgaucfpSNtYGqLiBmN0FcPWVw5lcmEb8/Io3SqIKj7pbhuf743n73wLU7b2TbNVjO3De8V0nZK2sY//mHG2Jm4HO7sBO/IcBJdOQohBHqjHiklkTFWxi0YjV6v/QeoKEWmrwX6i7JebOZkgYh+eX5MWK4F81/+CV4iCpHVlXN2fw+kY74/oQbwgLljSEKX0gW2HMk+mwOZ8b5/2KbpCqiyCGn/CbzHEeZ2YO6KEEaIGRGSOApSJhN+1zs6se2vnUF3+T6vj0s7XlKoczjtTpZ++xcblvxD9bpx3DSkG9XqBNf36fP4jaQlZzLzndmA/6ahz+M9GPBc6MYZh8OvkxcEXLTA3xfpdrj53/xROO0uImMiuOTKRhfck4tSMqR7FzLjPXBvzqoE+Zg/+RaREAIqTEIm34m/yJkLMIApHmG9o4DP6sCQx6xZUycwdQbnUvwJWQ8YIXpE0ASoIvMl+//4tXgOnI1TXxUR9bD2cWFQJhP+tQM7snDaUnYl7MWR4UBv1GMw6Hn6k0ewWM0Ffj7jdCZDrxxJ0rFkHJlODCYDP0+cx9hfn6d1l8CXKUII7hnTn4Ej+pD0XwqVqlfAHFFwG+eb9OQMze1Cp8Pr8V7wI46U0JLuncjk2/3dKEjwnUKeHoaMGY3QX4TM/MI/Nt7cBRF5T6EnOQljY6i6EhyLwHcSjG3AeFmxZsT6LyQTwLUa6fgddJEISx+EsVGRzxlEV8nf7aSV889xZnBJKrPDMr1eL2vnbmD1nHXEVomh+/1dqNn44kJ99vNR3zDz3bm4nYF915VrVOKbgx+WyTvcnyfN47ORX+O0BXZ5ma0mfjzxGRGRGrVIlHLLl/wQuJYRnOHM+Pviz3RtmEBXCVFlDkIXG84Qw84/9HMygd06FkSlL0q8Bn5O5W5YJoBer6dD77Z06N32nD+74sfVQckeICMlk2N7T1Cz0UWhCPG80uOBrsz/dAnH9p7AaXMidAKTxcQjE+5RyV4J5tmC9u1s7vdnLvClIG0zEFFDwxBY6RGRDyJFNGR+6H+6MTRCRI8Ma7IvSJlN+MVhzqPbx+fzYbEWsgZ3CKWnZPD1azNZOWstpggTNz98Pb0f647eELoXpxarmUlr/sei6Sv469e/qVgtlt6PdlfVMhVtuup514EP4gTHcijrCV8IRORAiMy3tFipUgk/h7TkdL55/ScSjyQhhAhYDUen11G/RW2q1Kgc1pgcNiePtR3BqSNJuLMKqH0+6hu2rdrFi98/HdK2zBFmej7UjZ4PdQvpeZWyR0Q9ijw9nMDuCxP+CVAac11yjZxRSkfZ64wuojOJdfbkBaQnZ2Qne71BR0S0hbhalXnpx2fCHtfSb/8k5cTp7GQP4LS5WDt3PQd3HAl7PIoCICzdIHoEiBj8JYDNEHErGJoQOJEIIAIReW/YY1SCqTv8LEu+WsHpk6kBiRUAIRg68X6uG3RNqbys3bxsm+YkMqET7Pp7D3Wa1sz3816vl18/WMCvkxdgS7dz5Y1tuHfsgLA/qShljy5yINJ6m79AmqiI0FnxeY5CyiDwHsOf+A0QPRJhOvd3aUroqYSfZfPy7ZqJ1WQ2otPrS21kzkUNqmE0G4IWQRE6QVytgpP2hCEfs+z7Vdlj7BfPWM7a3zbw2fYJxFSKLpGYlfJDCIO/jAFZZYBTHswqj+DDv4SgRBjyWPlJCTvVpZPl4gbVMJq0r39xNUvvbvjGwdcFvZzV6XVUiIstsC79yUOJ/PHtnwETqrweH7Z0O3M/XlQi8Srll8z8AryHc8xo9Ve8lKnDkTLnEp1OpG0mvpSH8aWOQrq3BZ5HSqRjAb6kO/Gd6o0vY4r/YqIUm0r4WW4c3BW9MTixVqxeIex1Y1JOppJyMhXwX2zGLRhN9XpVMVmMGM0GmrZrxDvLXinwqWPPxgOaFzGX3cWW5dtLJHalHHPMJ3hYJv7JWZ69/i+lA5nUH5n+Kjj/APssZNJAfLaZZw9PfxOZ+jy414FnB2R8iEy6FSlzly04v0lfMr70d/Gd6ocv5XGka1Nph6S6dM6oWjuO/80bxRt3T+L0yVR8Ph9N2jbkhW+GZSdWh83JmjkJpKdk0rpL80JP5CqsQzuP8r873uNQ1svY2k1r8sI3w2je8RKm7/mAxCNJmCxGKsQVbgJLtbpxeD3BRaP0Bj21moQ2dkUhrzLD0utfdASQtpng2c/ZuvA+/9dpryItN4JMB9tXBF44nOA9jrT94h/2eAGQ3kRkUi/wpQMu8PzjXwUs9nV0ETeXWlwhSfhCiM+BnsBJKWVzjf0CeB+4EbAB90opN4SibS3pKRksnrGcQzuO0ji+AZ1v71ioyUMtOjVlxr7JnDx0ClOEiYpVzybWnX//y4gbXsPn8+Hz+pA+SY8HuvLYxPtDshCyw+bkqU6js0YI+bft23yApzqN5qsDHxIRaaFqrSpIKfnjm5X89P5vZKbaaN+rLbc/34eYysH98Q1a1aXupTXZu+kAHvfZoXIGk4HeQ3sUO2ZFyUlY70SmvULgUE0dGOqe7cd3LEBzERCh99fkkWlZ67/mflKwg2v5eT3GPSeZ+RH4UoEz794k/gvbWKSlu79gWikIVZfONKB7Pvt7AI2y/jcE+DBE7QY5tPModzccymcvfMvcjxcxZdgX3N90GMnHg0sYaxFCUK1OXECy93q9vHjzeDJTbdjTHThtLlwONwunLWXN3PUhiXvlzDW4nJ6A+ktSgsvp4c9ZawFI+i+FB5oNY9xdE9m1bi9Hdv/Hz+//xiOXP0dmWu5KgH7/mz+K+O6tMZgMGM1GqteryutzR5bJ2cJKKYvoAxE9ALO/9K+IBF1VRIXJZ4/R5bVKmg90UaCrjPYMXh14DuI7dQu+1BeRnoOhjz+UnCs4m+xzcvvr/peSkNzhSylXCCHq5nNIb2C69A9uXyOEqCCEuEhK+V8o2s/p3cEfknnalj2O3pHpxO30MPW5rxgx/fEinXPH6t04HcFllR2ZTuZ/uoT2N2uWrTgnJw+dwqkxSsiZ6eTkoVPYMx08evlzJB8/HbDf4/Zy+mQq8z9dQr+ngx8VYypF8+qvz5OZZsNpc1KxWoWQPJEoSm5C6BCx45GRD4N7I+iqgqldwHq0wnon0vkXgU8BAkTFrAVLpD/pe3PXsPdllU32gWc70jEHKn2NMOY/cKHU6CppJ3bpAVF6NYXC9dK2BnA4x/dHsrYFEEIMEUIkCCESEhMTz7kRl8PFjrX/krsgnNfjZfXsded8vjM8bm+eSdKlUXOnKBq3bYAlMrikgyXSTOO2DVj6zZ+kn87U+CS4HG4Sft+c7/kjY6xUql5RJXulxAlDXUREX4S5Y9Di48LcEaIewv8UEJX1FFANUekzf2kCoUNU/BIMjQBL1ipRZ9KU7+x/pQ2ZNiZsP9O5EpH345+QllNWqWd9cJn1cDmvRulIKadKKeOllPFxcef+jyJ0AqGxJB+AwVj0h5lm7RsHXUTAn4wbtq7Hc93GcnfDoYy/exJH/i3aQ8vl3VpSu2kNTJazfXtGi5HaTWtwebeW7F6/F7dD++IihKB63dL7JVKUc6GLehRRdTki9g1ExamIuGWIHLXshaEmuipzEFVmQ8XpaK5WBeDeEp6Ai0BYboCoIWRf2LCAsRWiwoR8PyelRLp3I907Aoayhkq4RukcBXLOvqiZtS2kjCYjV/Rozd/zNuL1nH1JabIY6Xb31UU+r8li4rlpQxl/10S8Xh8elwdLlIWL6lXl54m/4bL7E/GJg4ms+vVvPlg7ntqXBD3A5Eun0/HWH2P4/s1fWTx9OQDXDbqa20f0RafTUadZTcxWU1D5YvC/hO3z+I1F/vkUpbiklOD6G7yHwNgUYQwauxFA6CqBJf+aTcJQFwH4siZwabSKlA6EOD+rueqiHkNa7wbPTv+7DEOdfI+X7u3IlEdBpuDv5oqEChNDWm0zZPXws/rw5+YxSucmYCj+UTpXAhOllFfkd76i1sNPOZnK09e8RNLRZHxeH0InqN+qDuMXvljsMr8nDiby+5fLSD2VRvwNrXjr3smkJQVOCBFC0LHPFbw8a3ix2sot43Qmgxo8FvB+AvxzBV788Rmu6pPvP6eilBjpS0Ym3QW+Y/6RBgIwtERU+iQkydh3vDnai5ALRNUEhO7CnzEufTZkYif/sNSchBUR98c5rcxV4vXwhRDfAp2BKkKII8DLZC0lL6X8CJiHP9nvwT8s875QtKulYtVYPts2gU1/bOXonuPUb1mHZu0bh6TvulqdOAa9dBsAp44mad5tSynZ+tfOYreVW1SFSCauep13B3/E9jW7EULQ8ppmPD/jcSpXrxjy9hSlsGTqKP96smdGpUjAvQmZMQkR/WzxGzB3B+fs4O36RkHJXrr/Bfd60MWB+epSG/6Ym5RSMwdJXyYy8zOwfwdSYzax9IJ9LkTeHZI4QjVKJ9/BsVmjcx4LRVuFodPpaHNdS9pc17LE2oisEInPp/10VOmiwi3ndq5qNanBhJWv4nK60elEsd5LKEooSOkC53KChyA6wTYLQpDwRcyzyKRVWZOYnIARhAlRYVyOOLzI1GfBsTjrQ3r/ZK9KXwe8H/CnIk9YLgRSSqTtS8j4EGQKUl8bEf0CwtIla7/bv0yk5wCaM5QBcCJ9iYRqqMV59dL2QhIRaeHagR0xRQQuiGKONDNwRN8SbdtkNqpkr5wnvGj3rwOEZgSb0FdDVFkI0c+ApQdEPoSosgBhPLu+tLTPAscS/JO6HCAzwZeMTPHfZ0op8WV+gTx5JfJEc3wnO+Ozzw9JfHmRmVMhfUJWnzzgPeRf99f5l/9752J/7aE8kz3+Lh3TlSGLSWWNYnhyyoO4nR7+/GktBpMe6ZPc9dJtdB7QEYC0pHQyU21UrVMFvT50q1MpyvlCiAikoRl4/sm1Rw/mLqFrRxedVVP/Xu0DbN8ROLYfQIL3KNJzEOlYGLjerO8YpD6PFBaE5dqQxZndsnRD5kcaMTmQGe8hzB2RznU5Cs1psYChBZg6hCwulfCLwWQx8cLXT5KWnE7yf6e5qH5VzBFm0lMyGD9oIhuX/IPeoMdsNfPkh0PodEvortSKcr4QseOQyQNBuvHfYUeALjo0/feFJbVe6gJC5y+6lvkx2sl3QokkfHxp/klWWjz7/f/V18C/6HvuO3wd6GpC5L0Ia3+ECF1HTJlN+CknU0FKKlYrmf70nGIqRQfUlh/T9y22r9mNx+XB7fTgyHTyxt0TqVp7LE3iG5R4PIoSTsLYGOIWIW0/gXevf4RORC+ELjJ8QUT0zLqDz5U8RaR//V2pUb8HsrpUSoAuFoRJoyYQkPVOQVj7IjM/yHWMAF0lRNz8EnnPUOb68I/sPsaj8c9zZ52HubPuowxp9Qz7tx4KW/tH9/zHznV78ORaOcvlcDPz3Tlhi0NRwknoKqGLGowudhy6yIHhTfaAsN4NhgaANWuLCUQEIvZdhC7GX9tHi76+9vbixiMMEPUowbNtLYgo/1rUQlcJUXEa6GsCFn/MhksQlb4psZfKZeoO32l3MqzTi6SdSs8eq35g6yGevuYlvj7wIdboPMq3hlDSsRSMJgMue+AjpvRJju87UeLtK0p5JHRWqPwjOBYhXatBfxEi4haEvjoAMmoYpL9JYLeOBRFdcutUC+v9SKyQOQV8p0BfDxEzEmFud/YYUyuosgS8R0AYs+MtKWUq4f/1yzpcdlfAxCQpwePysOz7Vdw4uGuJx1CvRW3cGvV1jGYDl3XJf/ahoihFJ4QRIm5ERATPOtdF3olPREDmJPCeBEN9RPRzCHPoXogGxyP89fsLKOkshIAwLQNZphL+yUOncGnUm3FkOkk8fCosMURXjOLWp3ry88R52Wvk6vQ6LFYzPR4o+QuOoijadNZbwHpLyM4nXRuRtq/AlwLmbghr3/O2zMMZZaoPv0nbBgHFx86IiLLQpG3DsMVx32sDeerjh2jYui5RFSPR6QQup5vBLZ7mrfsnh6zCpqIopcOX+RUy+R5wzAXXn5A+3r90Y14vh88TZSrhX3Ztc+q3rBOQ9E0WIzUaXUTbHpeFLQ4hBF3u6MSgl/vjdnrwuL04bS7cDjfLvl/FxMc+CVssiqKElvSlQ/ob+Iegnuk+toPnINL2cylGVrAylfCFEDww/g4qX1wJoRMYTAY69LmCd1eMLZWJT9+8/hNOW+CwLJfdxR/f/Ik948JakFlRlCzuTaA5isYOzoVhD+dclKmEv331LkZ2/x//7TuB9Ek8Lg+rZ69j7W+hWYbwXCUeSdLcrtPpSD2VrrlPUZTznIhGu0a/AN35XciwTCX8qc/NCLqjdtpcfPT0l5oLmJS0Szs01lyQxWgyEFezctjjURQlBIyt/EsyBpU0syCsd5RGRIVWphL+3k0HNLefPpmGLT38XSj3jL0di9UckPTNVjMPvnkXeoOqraMoFyIhBKLS56C7yD+TV0QBZogehjC1BUB69uBLfRVfyiP4Mr9B+vKrmRM+ZWpYZuWLK3FUY4lBk8WouV5sSavTtCaT1o7jy5e/Z8fq3cTVqsydo27lyptCt4KNoijhJwz1IO4PcG8GmQrGNv4ZvYB0LEGefgp/tVAvOFchbdOg8qxSX6ylTCX8O0ffyvuPfBLQrWO2mun75I2lVq2yTtOavPRDyc3mUxSldAihA1PrgG1SepCpI/GP4DnDDt7/kJnTENGPnz3WdxpcG0AXDcbLQ1okLS9lKuF3G3QNaUnpTB/zQ9aatoJej97A3WP6l3ZoiqJcYKR0gWu1v/CaqR1CF1vwhzz/or0OgBMcCyAr4fsyP4P097JG+0j/i+BKXyAMJVtcsUwlfIBbh/Wk92PdOX0ylZjK0ZgspoI/VACv18s/K3aQnpxB86suCUsFTkVRSo90bUCmDMG/wAsgPciY0eisA/L/oIj0L0uoJas7R7rWQfpEwHm2Uqa0IZPvh7ilJXqnX+YSPoDBaKBKjdCMgjm08yjPdRuLLc2OANxuDwOe68M95/FTgz3TwR9fr+SflTu4uGF1bhzcNWT/HopS1knpQKYMDl5jNu11pLG1vxx0HoShNtJQDzy7CBy6GYGwDvKf3/Y1gV0+ABJkGri3gKnkJomG5FIihOguhNglhNgjhBihsb+2EGKpEGKjEGKLECK4utF5SErJCze+TvKxZOzpdmzpdtwONzPfmU3C75tLOzxNaUnpPNjiaT565kuWfL2S78b/zP1Nh7F9ze7SDk1RLgzOFWgv2+j2L6VYAFFxir/ksbBmjeAxgbU/WLLSnu90HucXIEt2fk6xE74QQg9MBnoAzYCBQohmuQ4bDfwgpWwN3A5MKW674fDvhn2knkon9xB+R6aT2VMWlE5QBZjxyo8kHUvJLtzmdnqwZzh48+5JpTIXQVEuODIT7YTs9d+FF0DoayCqLEJU/AwROw4RtxhdzCh/VUwAc3eC6+TjXyHL2Dp4ewiF4g7/CmCPlHKflNIFfAf0znWMBGKyvo4FjoWg3RJnT3eg05g4BZBxOjPM0RTOyp/XBi2+AnDySBLJx0+XQkSKcoExdYAYhwAAACAASURBVNBenlBYEebrC3UKIQTCdDnCckNQjXth7Zu16tWZpC8AC0SPQOiiihV6QULRh18DyLlO2BEg9+KtY4DfhRCPA5HAdVonEkIMAYYA1K5dOwShFU+TKxri8wZPoTZbTVzTv+TqaBeHWaNaKAA+idFcJl/ZKEpICX01ZNSjkPEx2QXShBWMbcF8TfHPL8xQ+Tuwz0Y6fgd9JUTEHf7FUEpYuGbaDgSmSSlrAjcCM4TGq2gp5VQpZbyUMj4uLi5MoeXNYjXzxJQHMUeY0On94VoizdRqUoPu95XAwsch0PPh6zFbA0cm6fQ6mrZvHLDurqIoedNFPYqo9AVE3AKWGxGxbyAqfhSyETRCmBHW29BV+gRd7BthSfYQmjv8o0DO5VpqZm3L6QGgO4CUcrXwrxJQBTgZgvZLVLdB11C/ZR3mfvQ7KSdO075XW64deBUmc8msOVlctzx5E9tX72bd/I0InUAIQcXqFRj59ZOlHZqiXFCEqQ3C1Ka0wwgpUdwXeUIIA7Ab6Io/0a8D7pBSbstxzHzgeynlNCFEU2AJUEPm03h8fLxMSEgoVmzl2YFth/l3/T7ialWm5TXN0OnKVNkkRVHyIIRYL6WM19pX7Dt8KaVHCDEUWAjogc+llNuEEGOBBCnlbOAZ4BMhxFP4X+Dem1+yV4qv7qW1qHtpeNbJVBTlwhCSt3hSynnAvFzbXsrx9XagYyjaUhRFUYpGPecriqKUEyrhK4qilBMq4SuKopQTKuEriqKUEyrhK4qilBMq4SuKopQTKuEriqKUEyrhK4qilBMq4SuKopQTKuEriqKUEyrhK4qilBMq4SuKopQTKuEriqKUEyrhK4qilBMq4SuKopQTKuEriqKUEyrhK4qilBMq4SuKopQTKuEriqKUEyrhK4qilBMhSfhCiO5CiF1CiD1CiBF5HNNfCLFdCLFNCPFNKNpVFEVRCs9Q3BMIIfTAZKAbcARYJ4SYLaXcnuOYRsBIoKOUMkUIUbW47SqKoijnJhR3+FcAe6SU+6SULuA7oHeuYx4EJkspUwCklCdD0K6iKIpyDkKR8GsAh3N8fyRrW06NgcZCiL+EEGuEEN21TiSEGCKESBBCJCQmJoYgNEVRFOWMcL20NQCNgM7AQOATIUSF3AdJKadKKeOllPFxcXFhCk1RFKV8CEXCPwrUyvF9zaxtOR0BZksp3VLK/cBu/BcARVEUJUxCkfDXAY2EEPWEECbgdmB2rmN+wX93jxCiCv4unn0haFtRFEUppGInfCmlBxgKLAR2AD9IKbcJIcYKIXplHbYQSBJCbAeWAs9KKZOK27aiKIpSeEJKWdoxaIqPj5cJCQmlHYaiKMoFRQixXkoZr7VPzbRVFEUpJ1TCVxRFKSdUwlcURSknVMJXFEUpJ1TCVxRFKSdUwlcURSknVMJXFEUpJ1TCVxRFKSdUwlcURSknVMJXFEUpJ1TCVxRFKSdUwlcURSknVMJXFEUpJ1TCVxRFKSdUwlcURSknVMJXFEUpJ1TCVxRFKSdUwlcURSknVMJXFEUpJ0KS8IUQ3YUQu4QQe4QQI/I57lYhhBRCaK63qCiKopScYid8IYQemAz0AJoBA4UQzTSOiwaeBNYWt01FURTl3IXiDv8KYI+Ucp+U0gV8B/TWOO5V4A3AEYI2FUVRlHMUioRfAzic4/sjWduyCSHaALWklL/ldyIhxBAhRIIQIiExMTEEoSmKoihnlPhLWyGEDngXeKagY6WUU6WU8VLK+Li4uJIOTVEUpVwJRcI/CtTK8X3NrG1nRAPNgWVCiANAO2C2enGrKIoSXqFI+OuARkKIekIIE3A7MPvMTillqpSyipSyrpSyLrAG6CWlTAhB24qiKEohFTvhSyk9wFBgIbAD+EFKuU0IMVYI0au451cURVFCwxCKk0gp5wHzcm17KY9jO4eiTUVRFOXcqJm2iqIo5YRK+IqiKOWESviKoijlhEr4iqIo5YRK+IqiKOWESviKoijlhEr4iqIo5YRK+IqiKOWESviKoijlhEr4iqIo5YRK+IqiKOWESviKoijlhEr4iqIo5YRK+IqiKOWESviKoijlhEr4iqIo5YRK+IqiKOWESviKoijlhEr4iqIo5URIEr4QorsQYpcQYo8QYoTG/qeFENuFEFuEEEuEEHVC0a6iKIpSeMVO+EIIPTAZ6AE0AwYKIZrlOmwjEC+lbAnMBN4sbruKoijKuQnFHf4VwB4p5T4ppQv4Duid8wAp5VIppS3r2zVAzRC0qyiKopyDUCT8GsDhHN8fydqWlweA+Vo7hBBDhBAJQoiExMTEEISmKIoSHl6vl01Lt7Ji5mqSj6eUdjiaDOFsTAhxFxAPXKO1X0o5FZgKEB8fL8MYmqIoSpEd3nWU564bS2aaHSHA7fRw2/Cbue/VgaUdWoBQ3OEfBWrl+L5m1rYAQojrgFFALymlMwTtKho8bg8/vD2bexo/zh11HmHqczPIOJ1Z2mEpSpklpWTUTeNIOpaMPd2OLc2O2+nmp/d+Y+28DaUdXoBQJPx1QCMhRD0hhAm4HZid8wAhRGvgY/zJ/mQI2iyzDu44wubl28hMsxV8sIYxt7zF9DHfc2zPcRIPn+KXSfN4vP0LuJzuEEeqKArA3s0HSDlxGpmrT8KR6WT2lAWlE1Qeit2lI6X0CCGGAgsBPfC5lHKbEGIskCClnA28BUQBPwohAA5JKXsVt+2yJPl4CqN7juPQzqMYjAbcTg/3jB1A/+GF/2f6d8M+Ni3dhtPmyt7mdno4dTSZFT+u5rq7ri6J0BWlXLOnO9Dpte+dM0/b8Hq8zP5wIb99vAi300PnAR3o/1xvImOsYY40RH34Usp5wLxc217K8fV1oWinLHu571vs23IQr8eHE3/CnjHmB+o1r0Xb7q0LdY5d6/YSdJsBODIcbP1zp0r4ilICGsfXR/qC/+7MVhPXDOjAa7dPYN2Cjdk3Yj++M4e/fvmbKevfxGQ2hjVWNdP2PPDfvhPsz0r2OTlsTmZNmFvo88TVqozOoA/abrIYuahB1WLHqShKMHOEmSc/GoI5wpR9p2+JNFOz8cVccmWjgGQP4Ha6OXHoFCtnrgl7rGEdpaNoS0tKR2/Ugz14X8qJ1EKfJ/76VkRVsOK0OfF5z1489AY9199zbShCVRRFQ9c7OlG/RW3mfryIpP9SaH9zPNcOvIrF05drHu/IcLB5+Ta63tkprHGqhH8eqNeituYjodFsoH2v+EKfR2/QM2HFq7x+x3vs2bAPIQRxtaow8qsnqFg1NpQhK4qSS70WdXj8g8EB2yrXqIRer/3UXb1u+J+6VcI/D5gsJh55714mP/E5LrsLKf2/ELFVYrhl2E3ndK5qdeKY+NfrpJxMxePyUKVGJbJelCuKEmbx17fCGhuBI9OBL8dNnd6g54b7wv/UrRL+eaLH/V2p1aQGsybMJelYMlfc2Ibej3UnumKU5vFej5d/N+zDYDTQ4LK6QUk9vzt6r8fLkq9X8vv0ZegNenrc34Wrb2uPTqde6SjnxuvxotPr1E1FHvQGPe8uH8ur/d/l4LbDCJ2gQlwsI756gsoXVQx7PEJqjOo4H8THx8uEhITSDuO8tH7RZl4f+B5etxcpJVEVIhn76/M0bF2vwM9KKRl98zi2LN+OI9M//80SaaZj3ysZMf3xkg5dKSPWLdzE5Cc/59i//xERHcEtw3py14u3anZfKH6njibhdnqoXq9qiV4ghRDrpZSafcHqlu4Cc+poEi/3fYv05Axs6XbsGQ4SjyTx7HWv4LQXPIF509KtbFm+IzvZg3+CyJ8/rWHPpv0lGbpSRmxbtYtXbnmLo7v/Q0qwpdn58e3ZTB0+vVTisaXbWf7DKhbNWE7KycIPcgi3KjUqc1H9aqX6NKQS/gVm0YzlASNwzvB6vKyZs77Az29c8g+OTEfQdp/Hx6Y/toYkRqVsmzH2R5x2V8A2p83Jb1MXY8/QGGqWh0M7j/LpiK94/5Gp/D1/Iz5f8O91QdYt2MiAix/knQc/YuJjn3JX3UfOu9mt5xPVh6/hyO5j/PD2bPZvOUjj+Ab0e/pmLqpfTfPYLSu289WrP3Jk9380bF2Pu8f0p+FlBXetFFXy8VTcGmUSvG4fpxPTCvx8bJUYTBYjLkfgOQwmAzGVo0MWp1J2HdpxRHO7Tq8j6VgKNRtHFHiOhdOWMumxT/G4vXg9XhZ/vZJWnS/llZ+fLXS3UGaajVf6vYPTFvhkO/XZGbS6tjl1mqoq7LmpO/xcdqz9l0cuf46FXyxl5997+G3qYh66bDh7Nx8IOM5hc/LWfZMZfu0YNi7ZSuLhJFbPTmDYVS+ya92eEosvvltLLFGWoO1CB606X1rg57vccRVC6+WsEFx1y5WhCFEp4+q3qotWr4TPJ6lSs3KBn89MzWTiY5/itLvwerxA1rj0pVtZ9Wvh39utmbMenS44EI/bw+IZ2uPfi2LPxv2M7f8OD1w6jPF3T+JgHhe8C0G5Sfhej5f1izazctYaTifm3c838bFPcGSenbjk9XixZziYMuyL7GPcLjdPdXqR379cRu6X3k6bk49LsC8zvvtlNG5TH7PVnL3NEmnm6n7tqXvp2aKliUeSWDRjOavnJOB2nb2br1itAq/8/CxRFSOxxkQQEW2hQtVYxi8YhTW64DszRblnTH9MEeaAbRarmVuf7onFas7jU2dtXrYdgzH4Lt6R6WTZd38WOg6n3YVXs3vTF/COqjg2Ld3KsE6j+XPWWg7tOMrSb/9k6BUj2L1+b0jOH27loktn7+YDjLjhNVxZ/Y4et4e7x/RnwHN9Ao7zer3s3XhA8xzbV+3O/nrlrLUc2X0sz/Z2r99X/KDzoNfrGf/7aBZ89geLv1qBwWTgpiHd6DygQ/YxX7z4LT++MweDQY8QAr1Rzxu/v0ijNvUBuLxbK348/ik7/96DTq+jSdsGanSFUmiN2tRn/MLRfPTMl+zddIDYKjEMeL43fYb2KNTnjWbttCMEATcyBWnb/TLN7k3wlxkJhUlDPw0oi+Dz+i8mHz41jQkrXg1JG+FU5hO+1+tlZI/XOZ3r7f2MsTNp1r4JLTo1zd6m0+kwW02adwfWmLN3vxsWbc73DqJitZKd1Wo0Gbn5kRu4+ZEbgvZtWLyFn977DbfDjZuzfwyjbvof3x75ODuxG4wGmne8pETjVMqu5h0v4YM144r02cu6NNec82G2mul+f5dCn0dv0KHTCbwas9TXLdhE/+G9NT5VeB63h8M7tW/sdq0r/h2+z+djx5p/saXZaNa+MZGxkcU+Z0HKfJfOtr924dRIzi67k7kf/x6wTQjBjQ9ehynCFLDdHGGi92Nnk2vlGpUwmLTviA1mA7eP6KO5Lxx+m7pI82LksDnZvmo3HreHLSu2s3n5toCuHkUJF6PJyKtzRmR1KUZgiTRjNBvp90wvWl7dLM/PHdxxhOFdxnCDcQA3R9/FlGHTgv5Wzzh1JLnYceoNesxW7fNHV9KeEFlYB7cf5q66jzKyx2u8dvsE+l88JCyji8r8Hb493Q4aL5ikhIzTwYuMPDDuTk4dTWbNnASMZv9olk792nHn6H7Zx/R4oCuzJszF4/IGff6OEX25cXDpVYO2ZQQPuQT/xWz7mt283PfN7BdlOp2O0d8/xeXdWoUzRKUcSDySxOwpC9j/zyEuubIRNz98PbFVYrL3N+94Cd8f+4S1v23Anm6nTbeWVK1VJc/zJR9P4ckOo7Cl2ZDS39+/6te/gyrMgj9Rt+7avNg/gxCCXo/cwK+TFwQMQzVbzfR7qmeRz+v1enn+htdIPpYcUM186nMzaBzfgEuuaFScsPNV5hN+86suweMOTsyWSDOd+3cI2m4yG3nx+6dJPJLEsT3Hqdnk4qAp0NXrVuXlmcMZP2gSbpcbn9dHxaoVePmn4SU6JLMwrh3Qka0rdwTd5XvcXr4a+2PQ9jF932LG/smYrWbmfPg7K2etISrWSq/HutP+5sIXblOUM3av38vwLmNwOz14XB42LvmHn97/jcl/j+eiemeHN1usZq65rX2hzjnno99xOdwBCdLt9KA36DBFmLLfz+kNeqwxEQwceUtIfpb7Xh9IalI6S7/9E4PJgMfl4aYHu3Lr00VP+Nv+2pV94crJZXcz58PfVcIvjsjYSB6ZcC8fPTUNt9ONzyexRJpp0KounW8PTvhnxNWsTFw+Q8zadm/ND8c/Yf+WQ5giTNRqcnHQDLqD2w9zOjGNRm3qh20ETJc7rmLhF0vZvWEfjgwHeoMOg9FA59s7sPz71UHHSylZPH0FC79cyrG9J7L/cLb+tZO+T97I/a/dEZa4lbJjwpCPsaeffdJ0Odx4XB6mDp/By7OGF+mc/27Yr/mC1mw10/ux7mxfvZtTR5No3bUFA0feku/f7rkwGA0M/+xRhrw5iBMHE7mofjWiKhSvrz3jdKbmbFspJamnCp5LUxxlPuED9BzSjSbxDfht6mLSktO5qs8VtOx8KQe3HeHihtXzTcYnDiaScuI0dS6tRURk4Ph3vV6vWb/m1LFkRvccx5Hdx/zLFbo83P/6QG4dVvS7gsIyGA28ufglVs1OYNXsdcRWjqbH4K6snp2A2+UJOt7lcLNlxXaO7z+ZnezB/8g885259Bnag0rVw1/kSbkwOe1O9m05GLTd55MkLNpc5PM2vrw+GxdvCZow6HV76XpnJ+5/PTQ3JicPn+LHt2azZcV2LmpQjQHP9aHplY2IqRwdsomJzTteovm3aIk0c9Ut7ULSRl7KRcIH/1CyYR8NweVw8eZ9k3n7gQ8xmg143V76Db+Ze8YMCLjqpiWn88qtb7Nz7b8YTAa8Hh/3jh1Av6dvLrCtl3qNZ/8/h/B5zy5X+MXo76jXvDZtrmtZYj/jGXqDnk63XEmnHBOpHJlOvnp1Znb//Rlmq4n0lAzNF71Gs4Ftq3YHnEdR8mMwGtDpdZrlPwozRj8vPR/q5h995jzbrWOyGLn0qkuo06xW/h8upP/2neDR+OdxZDrwuL3s/+cgCQs38fz0J0L6NxBTOZr7Xr2dL1/+AZfdiZT+J5Val9Sgyx1XhawdLWV+lE5uHzz+mf9u1+nGlmbHaXcx6525/D5tWcBxrw2YwPZVu3A5so6zOfnype9Z+1v+9WqO7D7GoZ1Hg37hnTYns94r/HKFodYkvgEd+16BJTJwwlbb7q2pc2ktzUWY7RkOvn5tJn/+vDZogpmiaNEb9Fzdr33QWHtThImbhhR9MEOl6hV5f9XrtLq2OTq9DkukhR6DuzL2l+eKG3K2aS99hy3Nlv3OT0pw2lxMeuyTItX5yc9tz/Ri3PxRXDOgI5df34pH37uP91a+WuJr3IakPLIQojvwPqAHPpVSjs+13wxMBy4HkoABUsoD+Z2zJMojuxwu+lS8V7MvsGaTi/lix/uAv0vm7oZDcTuCj2vV+VLe/mNMnm1sX72LkT1ex5YWXESqUZv6TEl4o+g/QDH5fD7+/GktC75YClJy/T2dufq29hzcdpjH270QVBDrDEukmb5P3Biyx2albMtMszHqpnHs2bgfvUGHx+Uh/obLGP39UxhN4V20+1wMuPhBko+fDtpuijDxxc738x1FdD7Jrzxysbt0hBB6YDLQDTgCrBNCzJZSbs9x2ANAipSyoRDiduANYEBx2z5XtvS8K/ml5ig8lnYqHYNRr5nwk/5LybeN+q3qaj7OGi3Gc1qusCTodDqu7teeq/sFjoyo16IOT3/6MO89PBWP2xv0czsyncycMJe+T96klkpUsp1OTGXmO3P4e/5GKl9ckX5P38zl3VoRGWPlvZWvsm/LQY7++x/1WtSmZuOLSzvcAsXGxWgmfOmTRMZaSyGi0AtFl84VwB4p5T4ppQv4Dsg9xa038GXW1zOBrqIUikLHVokhtkrwixchBM2vOjvrtGaTixEag/cNRj1tu1+WbxsWq5mH3rknYMKGyWKkYtVY+jxeuKnnpaHLwE7MPPEZDVrV1dxvNBnYsWa35j6l/DmdmMqQVsP56b3f2P/PIRIWbublvm/xywfzs4+p37IOnW5td0Eke4DbhvcK6PIEMJqNdOgdT2TMuSd8l9PN0u/+YsbYH1n501o87uAXteEWioRfAzic4/sjWds0j5FSeoBUIGjclBBiiBAiQQiRkJiYGILQgs7P0EkPBCRjnV6HJcrMA+PuzN5mMht5eEJg0jaYDERViAyqv6Ol55BujJs/mo59r6Bpu0bcMeoWPt70dp7LFZ4vTBYT9VrU1uzPlz5JxWoVSiEq5Xw08905ZCRnBIw2cdqcfDbyaxy20BQuC7fr7rqaW5/uiclixBoTgclipHXX5jzz6SPnfK7EI0nc02goE4Z8xPRXfuCt+z5gcPOnSUtKL4HIC6/YffhCiH5Adynl4KzvBwFXSimH5jhma9YxR7K+35t1zKm8zluSSxxuX72Lb8f9zNE9x2nWvjEDR/alRsOLgo7bvGwbP7w9m1NHkrj8+pbc9kyvMp/09m4+wJMdRwUUjNLpdVzcoBqf73hfrV2qAPBQ6+Hs2xw8/NIaE8H4hS/S9MrAyUM+n4+0pHSsMdYSfzFZXJmpmRzaeYwqNSoVeTz/qJ7/I2Hh5oDuXYNRT5c7OvHsF4+FKlRNJdqHDxwFco6Lqpm1TeuYI0IIAxCL/+VtqWjWvgmvzh5R4HGtOl9aqBrzZUmDVnV59vPHmPDQx0ifxOvxUrPJxYz95TmV7JVslS+uqJnwPW4vFarGBGxb/uNqpjz5OekpGQghuOH+Ljzy7j3n7QvcyNjIoAvWufB6vaz/fXPQuzyP28vKWWtKPOHnJxQJfx3QSAhRD39ivx3IPZxjNnAPsBroB/wh1Ti/Qkk9lcZfP/+Ny+Hmypva5LnyVihd078DHfq0Zf8/h7DGWKnZKPjpRynfbnumF1uW7whYbcpg1NOoTf2A8gmblm7lrfs+CHhi/P2Lpbgd7iJ1lSjFU+w+/Kw++aHAQmAH8IOUcpsQYqwQolfWYZ8BlYUQe4CngYJvrxX++uVv7qzzCB8+PY1Pnp/B4OZPMf2VH8LSttFkpPHlDVSyVzS17tKCIW8NwhJpzu7vvuTKRrzy87MBx3392qyAZA/+hUuWfL2SzNTMcIYcNnq9nvgbLgt6F2Yw6unUr12pzmkJyTj8klCSffih4vV4+XbcT/zywQJsaXaadWjMoxPuo37LOsU+d2ZqJgNqDAn6YzFbTbyz9BWatG1YqPi+e+MXfv1gPrZ0Oy2vvpSH372H2pfkfqeuKEXjtDs5sPUwsXExVK9bNWj/XfUe5cTB4AEYEVEWJq8bT60mZfN38dTRJJ7oMIqM05k4Mp2YI0wIIbLnALW7OZ6hkx4IKswYCvn14Ze7mbah9O6Qj/jujV9ITUzD7XSzeek2hl01mv/2nyj2udfO26g5WsblcLP4qxWFOsc7gz/k23E/kXIiFafNRcLCjTzebiQnD+f5rlxRzok5wkyTtg01kz1AkysaIjTWnZVAtTpxJRxd6alSozJf/juJZz59lEEv3kZElMVfRM7txeP2snr2Op5o/0LY16RQCb+Iko+nsOy7v4LuwF1ONzPfmVPk82amZvLukI94+/4pARUHs0mpWe45t1PHkln2/aqA+KT0zzb+qRRLPCjly90v34Y5whyw6Lkl0sydo27BZNFeXKSsMJqMXHNbe+q1rI3D5gyoY+X1+EhPzmDVL+vCGpNK+EV0eNcxjBrDy7xuL7vW7SnSOaWUDO/6CoumL89zrU6z1Rywfm1eDm0/gskSHJ/H5WXH2qLFpyjnqk6zWrz/12u07dGaqIqR1G5agyc/HFKo+SxlxaEdRzVX3bNnODi0I/eAxpJVbqplhtrFDaprJmWdXke9FkXrw9+yYjtHd/+HR6N0KviTfde7rs53GbgzLmpQTTM+vUFHveahqS6oKIVRv2UdXp/7Qr7HnDx8ig2LthARHcGVN7UpVmXN4pBScmjHETJO22jYui7miOLHUadZTcyR5qAn9ogoC7Wbhvcdhkr4RRRXszJX9ryctb9tCKgjbzIb6f9sr3w+mbdD24/g1ajDA9CwdT2emPJgoccHX1SvGm2ua8mGXDXEjSZjoUo8K0q4TH/lB75/4xd0el1Wf7/g9bkjadGpaVjjOH7gJKN7juPEgUR0Bh0+n+SJyYNp1/Nylny9kmN7j9OsXWM69r3inOYQtOt5ORXiYnHZ3dndOnqDnpjK0XTo07akfhxNZW6Ujs/nI+VEKlEVrCG5OufH5XTzyXMzmP/ZH7jsLuq3qsMTkwfTrH2TIp1v4x//8HKfN7HnWpfWEmlmyJuDuPmRG/L4pDan3cmUp6axePpyPG4vdZrV5MkPh3Bph6LFpyih9s/KHYzs8XrAeH6AyFgrPxz/NGyzcqWU3NvkCY7vO4HPdzYnGi0GDAaDf20Lu4uIKAtxtSozcdXrRMYWfuWr04mpTHnyC/78+W9A0r5XW4ZOvL9EZu7nN0qnTCX8P75dyZRh0/wLl+OvjfHYpAdK5JfG6/WydeVO0lMyuLTjJcRUikJv0BfrnD6fj4dbP8vhXceyu3V0OkF0pWi+3DOpSAWczsTqdXvL/Esy5cLz1n2TWTR9WdD6rtaYCEZ9+xRX9Ggdljh2rP2X57uNDbrZ0mI0G+j1WHcefvueMER27srFsMwNS/7h3Qc/IjUxDZfDjcvhZsnXK3nvoY9D3tbBHUe4s+6jvNj7Dd66bzJ31X2EH976tdjn1el0vL10DFf3a4/B5F85qE23lkxa+78iJ3vwTwRRyV45HzkdrqBkD0DWiLJwSU1MQ6cxfFSL2+lh+ferSjiiklFmEv43r2vP6Fv2/SoyToduRp/P5+OFHq+TfCwZe7odW5odl8PNN//7iY1//HPO55NSsvXPHfw8cR6r5yQQGWNl5FdPMM/+DQtc3zFu/uiAqeqKUpZ07t8hqCQxgMfjpXWXUc3rVQAADY9JREFU5mGLo2m7RprrzOaluE/zpaXMvLTNa7KTwagn+fjpYq80f8audXtJT84IuitxZDqZ8+HvtO7SotDnctqdPH/9q+zddACvx4fBpCe6YhTv/flakav05cWeYef4/pPE1aoSsn8LRSmuDr3b0rprCzb+sRVHhgO9QY/BqGfoBw+cUx95cVljIqjZ5OKAgnA6gw6DQY/H5Qno1zdZjHS//9rs770eL3/P38h/+07Q4LK6tLy62XlbaLDMJPxm7Rpz6nBSwP8xZ1SvG7oZffZ0u+bMQYD0lIxzOtfXr83i3/X7skfRuJ1unDYXb94zibeWjCluqID/CeKzF77h54nz/Kt4OT1cf881PP7B4Av2LkUpO3Q6HWN+epb1i7aw6pe/iYy1cv2914a9/MfUZ2dwdPd/AdsEgn7Db+b3L5aRmWbH4/KgN+ho0rYh/bPmEZw6msSwq14kLTkdj8uDwWigzqW1eHPxS0REWsL6MxRGmUn4g17uz9rfNuDIdGYXJzJbzQx6+baQ9l83bdcIr8ZMV7PVHLR0IPiv/mvnbWDvxgNUr1eVTv3aZY8xXjhtWcCQSQCf18fWP3diS7djjY4odry/TJrHL5Pm47K7cGWt8Lh4xgqiKkQyePxd/jZ9Pjb9sZVNy7ZSsWoFrh3YkQpxailDJTx0Oh1tb7iMtjfkv5pcSfF6vMz/dEnQms5ej/f/7d17cFTlGcfx75OQKwG5qiA3QaIgVsQIKFhFbQXKiIoKeCMKCtJaC2PVSu1wUQel2EqbIhQQxSqoVcQiU+Q2KogIglx0JIhYY7jEIAGBhECe/nEOmU2ym91syJ5d9vnMZHJ29+zub8/svnv2Pe95H5a/8iHzduaw7r2N7P22gPMv60Cnnpnle/BT7vkHBXmF5VMhl5Yc5+tNu3h5/OuMnHJ3xF9LMKfVKJ1d275jzrhX+WLNVzRp0ZjbH7+Zqwf3OuXZlsxeTs5DcygtLqWsTEmtn0Lr81vy14+erPDlcrjoML+78gn27irg6E/FpGWkkpKWzPNrnqJlh7O59azhHPCppXtSYlIib+6dfUq6Xoa2HskP3++vcn1q/RTeKXqZshNlPP6rp/ny41yKDxeTnJZMQkICTy3+Q0gneBkTSarKilc/4u1pizlcdIReN3bntkcG0rBJ1dKloTpy6Cg3N83mxPGq58CkZqTy7sF5fu9XfKSEGxsP87sD2OjMM3hjz6ywM9VGXRdAiRrtLmzNxIWP1vnz9Bt+Leddci7vvrCUon0HueLGy+gztHeV4Z9z/7SA73N3U1riHAw6+lMxxUdKmJKdw18+nMSVt/RkyewVFc6sFXHOTDxV/ewHC/13M5UcPcbBwkMseGYh21Z/VX7y2Mn/kwY/x/y8GSQmWrePiR7Tx8xlyezlFLtTFbz1/HusWrCGmZunhv2LOC0jleatmrFn174qt3XumRnwflpW5swC54fvvDnR5LQZpRNpHbu1Z+zMUUxY+AjXZ/fxO9Z/1fzV5Y39SVqmfLkulyOHjpI9aQhntmlGaobT15eSnkL9RvV5ZO5vqjxWuDKz2vu9vkHjDO5oO5p/P7+4wpnCJ5UcLvFb0cgYr/zwfSH/mfF+eWMPznGvAwVF/PfFFWE/rojwYM4Idwpj5zqn1nUq90+5K+D90jLSyMzqUOUAbb2kRL/du9HAGvy6VM2RehFo2KQB/9zyHGNmjOSmh/pz37N38srOHNpdeOrmuhk1dRip6SnlB5pFnBNHjv5UzLHiY+gJ/7soCgEPThvjhe3rd5KUUrVTouTIMdYv/bxWj9293yVMWTGengOyaJXZkj5De5OzbjIdLm5X7f0enjOajMb1SXGPyzln4jbj3qeG1ipPXTmtunSizTW39+bd6UsrTGKWkCB0vjyTtAzn52dyShLXDO3NNUN710mG8y87j2lrn+ZfT75J7oadtOnUisL8/eR+9k2198tolB70zW5MJDVp0cjvKLyExISA8/HXRKceHZn4Ts26hNtccA7zduaw8rXV5OXmk3lpB3rf3CNqC7Vbg1+Hhk0YzKaVW9n99V5Kjh4jJT2ZtPqpES9ifG6XNvxx/tjyyyO6jAm4bkp6MvWS6jH+LStabqLL+Zedx5mtm5G3Pb9CgfCklHrcMLpm80ydSvUbpjNg5C88e/6aOO0afFV1xvQu+tQZ03v3VZ6VUUtvkMb0Dc+yYenn7HCHZfa6qbvn3/7d+3cjf8eeKmcWJqXU49fT7uXq264o/wViTLQQEZ55/wkm3jqVHRu/ITExkZS0ZB6eM5q2nW3K71DUalimiDQBFgDtgF3Abar6Y6V1ugLTgYbACeApVV0Q7LHDGZZZVlbGhEF/5rNlWyg+7Jy1l5iUyG9zRnB9dp/gDxAnDhQUMbLr7zm0/xClJccRgeS0FB78+3DbTiYmFOQVcuTQUVpltrCRZJXU2WyZIvIssF9VJ4vIY0BjVX200jqZgKpqroi0BDYAnVT1QHWPHU6Dv3rhOibfNa3CUXyA5LRkXs+fGdFTtaPdwcJDvP239/h0ySaat27KoDED6NLrAq9jGWNqqS7H4Q8ErnaXXwJWARUafFXd7rOcLyL7gOZAtQ1+OFbOX12lsQdnmNTGFVvpfVOPU/2UMath0wYMGz+YYeMHex3FGBMhtR2WeZaqnpyAYg9Q7bSOItIdSAa+DnD7/SKyXkTWFxQU1DiM7zjaymx6YGNMvAva4IvIMhHZ6udvoO966vQNBewfEpEWwDzgHlX1W8dPVWeqapaqZjVvXvMJz/ree035eNhKz03XCE61aowx0Shol46qXhfoNhHZKyItVHW326BXPTfZWa8hsBgYp6prw04bxEVXdmLQ2AG8MWURkpBAQqKzuz/xnUc9HxljjDFeq20f/iJgGDDZ/V+l7JOIJANvAy+r6pu1fL6gsicMof/wa1m/dDPpDVLpMeDSqJym1BhjIq22o3SaAq8DbYBvcYZl7heRLGCUqo4QkTuBF4FtPnfNVtVN1T12uEXMjTEmnsVNEXNjjIl3cVHE3BhjTPWswTfGmDhhDb4xxsQJa/CNMSZORO1BWxEpwBn5UxPNgB/qIE5dsbx1L9Yyx1peiL3Mp3vetqrq98zVqG3wwyEi6wMdnY5GlrfuxVrmWMsLsZc5nvNal44xxsQJa/CNMSZOnG4N/kyvA9SQ5a17sZY51vJC7GWO27ynVR++McaYwE63PXxjjDEBWINvjDFxImYbfBFpIiLvi0iu+7+xn3W6isjHIrJNRDaLiCf1/ESkr4h8JSI73Nq/lW9PEZEF7u2fiEi7yKeskCdY3rEi8oW7TZeLSFsvcvrkqTavz3qDRETd2Vw9FUpmEbnN3c7bROTVSGeslCXYe6KNiKwUkY3u+6K/Fzl98swRkX0isjXA7SIi09zXs1lEukU6Y6U8wfLe4ebcIiJrROTisJ5IVWPyD3gWeMxdfgx4xs86mUBHd7klsBtoFOGciTglHdvjlHf8HOhcaZ3RwAvu8hBggYfbNZS8fYB0d/mBaM/rrtcA+ABYC2R5lbcG27gjsBFo7F4+M8rzzgQecJc7A7s83sY/B7oBWwPc3h9YAgjQE/gkyvNe4fNe6Bdu3pjdw8cpoP6Su/wScGPlFVR1u6rmusv5OBW5al47sXa6AztUdaeqHgPm42T35fta3gSuFQlUnbfOBc2rqitV9Yh7cS3QKsIZfYWyfQEmAc8AxZEMF0Aome8DclT1RwBV9VtNLkJCyatAQ3f5DCA/gvmqUNUPgP3VrDIQpyiTqlOFr5Fbtc8TwfKq6pqT7wVq8ZmL5Qb/lBZQr0PnAN/5XM5zr/O7jqoeB4qAphFJV1UoeX0Nx9lT8krQvO7P9daqujiSwaoRyjbOBDJFZLWIrBWRvhFLV1UoeccDd4pIHvAe8GBkooWtpu/zaBL2Z662JQ7rlIgsA872c9M43wuqqiISSgH1YRqggLqpObeaWRZwlddZAhGRBOA5INvjKDVVD6db52qcvbkPROQiVT3gaarAhgJzVXWqiFwOzBORLvZ5O7VEpA9Og987nPtHdYOvMVRAvRrfA619Lrdyr/O3Tp6I1MP5SVwYmXhVhJIXEbkO54v3KlUtiVA2f4LlbQB0AVa5vWRnA4tE5AZV9aqkWijbOA+nn7YU+EZEtuN8AXwamYgVhJJ3ONAXQFU/FpFUnEm/vOyKqk5I7/NoIiI/A2YB/VQ1rPYhlrt0ThZQhygpoB7Ap0BHETnXzTMEJ7sv39dyC7BC3aMzHgiaV0QuAWYAN3jctwxB8qpqkao2U9V2qtoOp//Ty8YeQntPLMTZu0dEmuF08eyMZEgfoeT9H3AtgIh0AlKBgoimrJlFwN3uaJ2eQJFPF3HUEZE2wFvAXaq6PewH8vLIdC2PajcFlgO5wDKgiXt9FjDLXb4TKAU2+fx19SBrf2A7zvGDce51E3EaHnA+HG8AO4B1QHuPt22wvMuAvT7bdFE056207io8HqUT4jYWnK6oL4AtwJAoz9sZWI0zgmcT8EuP876GMyqvFOfX0nBgFDDKZ/vmuK9ni9fviRDyzgJ+9PnMrQ/neWxqBWOMiROx3KVjjDGmBqzBN8aYOGENvjHGxAlr8I0xJk5Yg2+MMXHCGnxjjIkT1uAbY0yc+D8E3KFM/xx8PwAAAABJRU5ErkJggg==\n","text/plain":["<Figure size 432x288 with 1 Axes>"]},"metadata":{"tags":[],"needs_background":"light"}}]},{"cell_type":"markdown","metadata":{"id":"bZyu2gJnxL5G"},"source":["The perceptron previously proposed allow us to solve a generic problem of binary classification, under the assumption that it is **linealy separable**, that is, the observation of different classes msut be separable by a line. If we try, for example, to learn the XOR function, returning $1$ if only one of the two input is $1$, then the perceptron fails"]},{"cell_type":"code","metadata":{"id":"qGBsmaD_xJyO","colab":{"base_uri":"https://localhost:8080/","height":201},"executionInfo":{"status":"ok","timestamp":1590664738987,"user_tz":-120,"elapsed":468,"user":{"displayName":"Alessandro TORCINOVICH","photoUrl":"https://lh3.googleusercontent.com/a-/AOh14Gi96E7HK6ff0uWSudqbJvEMactRTPtsT5-4448y=s64","userId":"03260776184459049943"}},"outputId":"cd6d8dd9-e6c3-4bb2-c42e-49e6beda26cc"},"source":["Xor = torch.rand(n, 2) # pun intended here :D\n","Xor = (Xor >= 0.5).to(torch.float)\n","yor_true = Xor.sum(dim=1) % 2\n","Xor[:10], yor_true[:10]"],"execution_count":null,"outputs":[{"output_type":"execute_result","data":{"text/plain":["(tensor([[0., 0.],\n"," [0., 0.],\n"," [0., 0.],\n"," [0., 1.],\n"," [1., 1.],\n"," [1., 1.],\n"," [0., 1.],\n"," [0., 0.],\n"," [1., 0.],\n"," [0., 1.]]), tensor([0., 0., 0., 1., 0., 0., 1., 0., 1., 1.]))"]},"metadata":{"tags":[]},"execution_count":21}]},{"cell_type":"code","metadata":{"id":"536qnHVQ1SKo","colab":{"base_uri":"https://localhost:8080/","height":283},"executionInfo":{"status":"ok","timestamp":1590664907654,"user_tz":-120,"elapsed":32467,"user":{"displayName":"Alessandro TORCINOVICH","photoUrl":"https://lh3.googleusercontent.com/a-/AOh14Gi96E7HK6ff0uWSudqbJvEMactRTPtsT5-4448y=s64","userId":"03260776184459049943"}},"outputId":"ed25b5e6-ffe6-4746-8d89-014b8d4a5672"},"source":["p = Perceptron().to(device)\n","delta_rule(pad1(Xor), yor_true, p, epochs=1000, eta=1.5, device=device)\n","\n","plot_decision_boundary(Xor, yor_true, p.w.to('cpu'), a, b)"],"execution_count":null,"outputs":[{"output_type":"stream","text":["ACC: 50.0"],"name":"stdout"},{"output_type":"display_data","data":{"image/png":"iVBORw0KGgoAAAANSUhEUgAAAXQAAAD4CAYAAAD8Zh1EAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAPFElEQVR4nO3df6xfdX3H8efrtqIxQ13W6zC0UsxKtNElkBvC4jZxwFL6R5vF4VrDnKazUQcu0WzBOJnB7A81c4um/qgJcTIVwT/M3axj6jBkxjouQVGKkFqVFu24ImNhRpD0vT++X8nlcm+/p9xz7/feT5+P5CbnfM6n5/P+9Hvv656eHz2pKiRJa9/EuAuQJPXDQJekRhjoktQIA12SGmGgS1Ij1o9r4A0bNtTmzZvHNbwkrUl33HHHT6tqcqFtYwv0zZs3MzMzM67hJWlNSvKjxbZ5ykWSGmGgS1IjDHRJaoSBLkmNGNtF0WfqxPGtwBPA7zJx1vXjLkeSOvuTjX/Oz378CABfPnFz7/sfeYSe5PokDyb57iLbk+RDSQ4nuSvJBb1XCZw4fiknjp/HIMwB/nO4Lkmr2/33389lE1c8GeYAl01cwevO2dvrOF1OuXwS2HaS7ZcDW4Zfe4GPLr2shdy/YKuhLmm127P5HQu2zx59uNdxRgZ6Vd0G/OwkXXYCn6qBg8ALkryorwIBThxfloN+SRq7P5p8Q2/76uOi6NnA0Tnrx4ZtT5Nkb5KZJDOzs7OnMMSjS6lPklatRx/6v972taJ3uVTV/qqaqqqpyckFn1xd2Lq3L19RkjRG7/zM23rbVx+B/gCwac76xmFbbyYm33ySrS/ucyhJ6t3Es7Lotj/Y9Xv9jdPDPqaB1w/vdrkIeKSqftLDfp9i4qz7Fmg9l4mzvtL3UJLUq1seu4lnP/eMp7X3feviyPvQk3wWuBjYkOQY8LfAswCq6mPAAWA7cBj4OfDGXiucY+FQl6TV718f/fSyjzEy0Ktq94jtBfxFbxVJkp4RH/2XpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRnQI9ybYk9yY5nOSaBba/OMmtSe5McleS7f2XKkk6mZGBnmQdsA+4HNgK7E6ydV63vwFuqqrzgV3AR/ouVJJ0cl2O0C8EDlfVkap6HLgR2DmvTwHPGy4/H/hxfyVKkrroEuhnA0fnrB8bts31HuDKJMeAA8DVC+0oyd4kM0lmZmdnn0G5kqTF9HVRdDfwyaraCGwHbkjytH1X1f6qmqqqqcnJyZ6GliRBt0B/ANg0Z33jsG2uPcBNAFX1DeA5wIY+CpQkddMl0G8HtiQ5N8kZDC56Ts/rcz9wCUCSlzEIdM+pSNIKGhnoVfUEcBVwC3APg7tZ7k5yXZIdw27vAN6U5NvAZ4E3VFUtV9GSpKdb36VTVR1gcLFzbtu1c5YPAa/stzRJ0qnwSVFJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUiE6BnmRbknuTHE5yzSJ9XpvkUJK7k3ym3zIlSaOsH9UhyTpgH3AZcAy4Pcl0VR2a02cL8E7glVX1cJIXLlfBkqSFdTlCvxA4XFVHqupx4EZg57w+bwL2VdXDAFX1YL9lSpJG6RLoZwNH56wfG7bNdR5wXpKvJzmYZNtCO0qyN8lMkpnZ2dlnVrEkaUF9XRRdD2wBLgZ2A59I8oL5napqf1VNVdXU5ORkT0NLkqBboD8AbJqzvnHYNtcxYLqqfllVPwDuYxDwkqQV0iXQbwe2JDk3yRnALmB6Xp8vMDg6J8kGBqdgjvRYpyRphJGBXlVPAFcBtwD3ADdV1d1JrkuyY9jtFuChJIeAW4G/qqqHlqtoSdLTparGMvDU1FTNzMyMZWxJWquS3FFVUwtt80lRSWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIa0SnQk2xLcm+Sw0muOUm/1ySpJFP9lShJ6mJkoCdZB+wDLge2AruTbF2g35nAXwLf7LtISdJoXY7QLwQOV9WRqnocuBHYuUC/9wLvA37RY32SpI66BPrZwNE568eGbU9KcgGwqaq+eLIdJdmbZCbJzOzs7CkXK0la3JIviiaZAD4IvGNU36raX1VTVTU1OTm51KElSXN0CfQHgE1z1jcO237lTODlwNeS/BC4CJj2wqgkrawugX47sCXJuUnOAHYB07/aWFWPVNWGqtpcVZuBg8COqppZloolSQsaGehV9QRwFXALcA9wU1XdneS6JDuWu0BJUjfru3SqqgPAgXlt1y7S9+KllyVJOlU+KSpJjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIa0SnQk2xLcm+Sw0muWWD725McSnJXkq8mOaf/UiVJJzMy0JOsA/YBlwNbgd1Jts7rdicwVVW/DXweeH/fhUqSTq7LEfqFwOGqOlJVjwM3AjvndqiqW6vq58PVg8DGfsuUJI3SJdDPBo7OWT82bFvMHuBLC21IsjfJTJKZ2dnZ7lVKkkbq9aJokiuBKeADC22vqv1VNVVVU5OTk30OLUmnvfUd+jwAbJqzvnHY9hRJLgXeBbyqqh7rpzxJUlddjtBvB7YkOTfJGcAuYHpuhyTnAx8HdlTVg/2XKUkaZWSgV9UTwFXALcA9wE1VdXeS65LsGHb7APBrwM1JvpVkepHdSZKWSZdTLlTVAeDAvLZr5yxf2nNdkqRT5JOiktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqRHrx13AqXjNb76R/5199Mn1v/7nt3LZ6149xookqZsTx68FbpzT8mwmzvpOr2N0OkJPsi3JvUkOJ7lmge3PTvK54fZvJtnca5XAZRNXPCXMAd5/5Uf40NWf6HsoSerViePbeGqYAzzGiePn9TrOyEBPsg7YB1wObAV2J9k6r9se4OGq+i3gH4D39Vnk9773vUW3/cu+f+9zKElaBkcW3XLi+NHeRulyhH4hcLiqjlTV4wx+zeyc12cn8E/D5c8DlyRJX0W+7RXX9rUrSVplLultT10C/Wxg7q+QY8O2BftU1RPAI8BvzN9Rkr1JZpLMzM7Odi5y3fp1nftK0tpyRm97WtG7XKpqf1VNVdXU5ORk5z93w9EPL2NVkjQ+E2d9t799dejzALBpzvrGYduCfZKsB54PPNRHgQAbNmxg3bMWPkr/8KH39jWMJC2Td6/IKF0C/XZgS5Jzk5wB7AKm5/WZBv5suPzHwH9UVfVXJvzbYzdy9Uf3PLk+sS58+cTNvPSlL+1zGEnq3cRZf8rEWffNa333Am1Lky65m2Q78I/AOuD6qvq7JNcBM1U1neQ5wA3A+cDPgF1VtfhlXWBqaqpmZmaWPAFJOp0kuaOqphba1unBoqo6AByY13btnOVfAFcspUhJ0tL46L8kNcJAl6RGGOiS1AgDXZIa0ekul2UZOJkFfvQM//gG4Kc9lrMWOOfTg3M+PSxlzudU1YJPZo4t0Jciycxit+20yjmfHpzz6WG55uwpF0lqhIEuSY1Yq4G+f9wFjIFzPj0459PDssx5TZ5DlyQ93Vo9QpckzWOgS1IjVnWgr4aXU6+0DnN+e5JDSe5K8tUk54yjzj6NmvOcfq9JUknW/C1uXeac5LXDz/ruJJ9Z6Rr71uF7+8VJbk1y5/D7e/s46uxLkuuTPJhkwTdYZOBDw7+Pu5JcsORBq2pVfjH4r3q/D7yEwTuavg1sndfnrcDHhsu7gM+Nu+4VmPOrgecOl99yOsx52O9M4DbgIDA17rpX4HPeAtwJ/Ppw/YXjrnsF5rwfeMtweSvww3HXvcQ5/z5wAfDdRbZvB74EBLgI+OZSx1zNR+hjfzn1GIycc1XdWlU/H64eZPAGqbWsy+cM8F7gfcAvVrK4ZdJlzm8C9lXVwwBV9eAK19i3LnMu4HnD5ecDP17B+npXVbcxeD/EYnYCn6qBg8ALkrxoKWOu5kDv7eXUa0iXOc+1h8Fv+LVs5JyH/xTdVFVfXMnCllGXz/k84LwkX09yMMm2FatueXSZ83uAK5McY/D+hatXprSxOdWf95E6veBCq0+SK4Ep4FXjrmU5JZkAPgi8YcylrLT1DE67XMzgX2G3JXlFVf3PWKtaXruBT1bV3yf5HeCGJC+vqhPjLmytWM1H6GN/OfUYdJkzSS4F3gXsqKrHVqi25TJqzmcCLwe+luSHDM41Tq/xC6NdPudjwHRV/bKqfgDcxyDg16ouc94D3ARQVd8AnsPgP7FqVaef91OxmgN9VbyceoWNnHOS84GPMwjztX5eFUbMuaoeqaoNVbW5qjYzuG6wo6rW8gtpu3xvf4HB0TlJNjA4BXPS9/Sucl3mfD9wCUCSlzEI9NkVrXJlTQOvH97tchHwSFX9ZEl7HPeV4BFXibczODL5PvCuYdt1DH6gYfCB3wwcBv4LeMm4a16BOX8F+G/gW8Ov6XHXvNxzntf3a6zxu1w6fs5hcKrpEPAdBi9eH3vdyzznrcDXGdwB8y3gD8dd8xLn+1ngJ8AvGfyLaw/wZuDNcz7jfcO/j+/08X3to/+S1IjVfMpFknQKDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUiP8HPeMxTlTE0gAAAAAASUVORK5CYII=\n","text/plain":["<Figure size 432x288 with 1 Axes>"]},"metadata":{"tags":[],"needs_background":"light"}}]},{"cell_type":"markdown","metadata":{"id":"sMJQsfGR7o6R"},"source":["The problem is not linearly separable and the perceptron learns a linear operator. To solve this problem we are going to modify the algorithm in two ways:\n","- Modify the step function with a more generic **non-linear activation function**\n","- Modify the delta-rule by using the algorithm of **Gradient Descent (GD)**\n","\n","As a new activation function, we use the sigmoid function:\n","\n","$$\\sigma(x) = \\frac{e^x}{e^x + 1}$$\n"]},{"cell_type":"code","metadata":{"id":"8ZeQGdab7nLL","colab":{"base_uri":"https://localhost:8080/","height":265},"executionInfo":{"status":"ok","timestamp":1590664861464,"user_tz":-120,"elapsed":733,"user":{"displayName":"Alessandro TORCINOVICH","photoUrl":"https://lh3.googleusercontent.com/a-/AOh14Gi96E7HK6ff0uWSudqbJvEMactRTPtsT5-4448y=s64","userId":"03260776184459049943"}},"outputId":"2d14292f-f587-4419-8ee6-f5d6e47648de"},"source":["px = torch.linspace(-10, 10, 1000)\n","tx = (px >= 0).to(torch.float)\n","sx = torch.sigmoid(px)\n","\n","plt.plot(px, tx)\n","plt.plot(px, sx)\n","plt.legend(('step', 'sigmoid'))\n","plt.show()"],"execution_count":null,"outputs":[{"output_type":"display_data","data":{"image/png":"iVBORw0KGgoAAAANSUhEUgAAAXQAAAD4CAYAAAD8Zh1EAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjEsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+j8jraAAAgAElEQVR4nO3de3xU1b338c8vISQi4ZqgYEBQoHITwUCx3rCIRREQKwgtp17a0tOj56k9rQfa+qhHPc9T2x5fnrYeW4rV6lFAjy1FDCpavLSC3ESQmw3KJSByC8g15LLOH3snDuOETMjM7NmT7/v1mtfs2XvN3r/smfyystbea5lzDhERCb+soAMQEZHEUEIXEckQSugiIhlCCV1EJEMooYuIZIgWQR24oKDAde/ePajDi4iE0ooVK/Y45wpjbQssoXfv3p3ly5cHdXgRkVAysy31bVOTi4hIhlBCFxHJEEroIiIZIrA29FgqKyspKyvj2LFjQYeS1vLy8igqKiInJyfoUEQkjaRVQi8rKyM/P5/u3btjZkGHk5acc+zdu5eysjJ69OgRdDgikkYabHIxs9+b2S4ze7+e7WZmvzSzUjNbbWaDTzWYY8eO0bFjRyXzkzAzOnbsqP9iRORz4mlDfwIYdZLtVwO9/MdU4NGmBKRk3jCdIxGJpcEmF+fcm2bW/SRFxgFPOm8c3iVm1s7MOjvnPk5QjCIp45zjqSVb2HOwIuhQmgfnyHLVZLsKWtQcp0VNBdk1FWS56hMe5qrJclVkEbmuhixX5W/z11EDgDnnLzvMP463XIM5/GV/Xd222td89t664cVd3b5r918fbz91P2DM93QcPI7egy9rwomLLRFt6GcB2yJel/nrPpfQzWwqXi2ebt26JeDQqfHwww8zdepUWrVqFXQokmQfHzjG3X9eC4D+EWqIoy2HKbADFHCAAvuUDnxKaztKPkfItyO05ij5HKWNv5xHBXlWSS7HyaWSPI6Tbc1vToZ32pwJaZrQ4+acmwHMACguLg7Np/jwww8zZcoUJfRmoLrG+1r+YsJAbriwKOBoAuYcHNgGezfB/i1QvuWz5093wOHdUFMZ+71ZOZDXBnLbQG4+5HXynnNaQU4etIh+5ELOad5zdi5k50BWi4hHdtRz9HILsCz/Yd4z5v9VtgbWEWc5i/orH7H8ub/+9Wzzl7/Y6A8jPolI6NuBrhGvi/x1oXT48GEmTpxIWVkZ1dXVTJgwgR07dnDFFVdQUFDAokWLeOWVV7jnnnuoqKjg3HPP5fHHH6d169Z0796diRMnsmDBAk477TSeeeYZevbsGfSPJNKw6krYuRrKVsCutfDJOti1Ho4f/KxMVgtoWwTtzoZzr4DTC6F1Jzi9E7Qu9J5PL/CSeE5ecD9LM5aIhD4PuN3MZuP94TmQiPbzf3thLet2fNrk4CL17dKGe8b0O2mZl156iS5duvDiiy8CcODAAR5//HEWLVpEQUEBe/bs4YEHHuDVV1/l9NNP58EHH+Shhx7i7rvvBqBt27asWbOGJ598kjvuuIP58+cn9GcQSYjqStj2Dmz6C2x9B7avgKqj3rbT2kOnfnDBZOjUFwp6eUk8vzNkp9WVzhKlwU/HzGYBw4ECMysD7gFyAJxzvwFKgGuAUuAIcEuygk2FAQMG8IMf/IBp06Zx7bXXcumll56wfcmSJaxbt46LL74YgOPHj3PRRRfVbZ88eXLd8/e///3UBS4JlZHN5xUHYcOLsHEBbFoEFQe8WveZ50PxLdB1KBQNhTZd1IEQUvFc5TK5ge0OuC1hEfkaqkknS+/evVm5ciUlJSXcddddjBgx4oTtzjlGjhzJrFmzYr4/8pJCXV4YPhk3Z3pNtVcLf2+2l8yrjkLrM6HvWOj9FThnuNe2LRlB/z9F2bFjBx06dGDKlCm0a9eOmTNnkp+fz8GDBykoKGDYsGHcdtttlJaW0rNnTw4fPsz27dvp3bs3AHPmzGH69OnMmTPnhJq7SEpVHIR3/xve+Q2Ub4a8dl4TyvmToGgIZGkYp0ykhB5lzZo13HnnnWRlZZGTk8Ojjz7K4sWLGTVqFF26dGHRokU88cQTTJ48mYoK71rlBx54oC6hl5eXc/7555Obm1tvLV7Sl/OvGw7tP1fHDsDiR2DJo1DxKXT9Ioy4B84b7V1BIhnNXED/YxYXF7voCS7Wr19Pnz59AoknEWon7SgoKEj6scJ+rtLVlr2Hufznr/PQxIFcPzhEly1WHYelv4W3/gOOlkOfsXDxHVB0YdCRSYKZ2QrnXHGsbaqhi8QQqhr65r/B/O/Dno1w7ggY8X+hy6Cgo5IAKKEn0ObNm4MOQZooVJ2iFQfhpR/Bu09Bu27wtWe9jk5ptpTQRcJo+wp4/lteh+fF34PLp0NL3cnc3Cmhi0SoraBbOl+JvmwmLJjmXX5403zofnHQEUmaUEIXCYvqSnhpupfQe30Frv+td1eniE8JXSSGtOsUPX4Y5vwDbHrNa2IZcY83OJVIBN1dEIdvfetbrFu3LqnHuOaaa9i/f//n1t9777384he/SOqx5TNBXcZ7UscOwFPXw4eLYOyvYeR9SuYSk2rocZg5c2bSj1FSUpL0Y0gIHS2HJ8d5ox/e8Dj0uy7oiCSNqYYe5fDhw4wePZqBAwfSv39/5syZw/Dhw6m9Ceqxxx6jd+/eDB06lG9/+9vcfvvtANx8881897vfZdiwYZxzzjm8/vrr3HrrrfTp04ebb765bv+zZs1iwIAB9O/fn2nTptWt7969O3v27AHg3//93+nduzeXXHIJGzduTN0PL6RV/fz4YXjmRm8Y20nPKJlLg9K3hr5gOuxck9h9njkArv7pSYvEGj730Ue9aVJ37NjB/fffz8qVK8nPz+fLX/4yAwcOrHtveXk5ixcvZt68eYwdO5a//e1vzJw5kyFDhrBq1So6derEtGnTWLFiBe3bt+eqq65i7ty5XHfdZ7+oK1asYPbs2axatYqqqioGDx7MhRfqbr9mp+o4PPsNKFsGE56A3lcFHZGEgGroUQYMGMDChQuZNm0ab731Fm3btq3btnTpUi6//HI6dOhATk4OEyZMOOG9Y8aMwcwYMGAAZ5xxBgMGDCArK4t+/fqxefNmli1bxvDhwyksLKRFixZ8/etf58033zxhH2+99Rbjx4+nVatWtGnThrFjx6bk55YTBTpSpnPwwveg9FW49mHoOy64WCRU0reG3kBNOlkaGj73ZHJzvcGPsrKy6pZrX1dVVZGTk5PweCWx0qJPdMl/wXvPeDcLXXhT0NFIiKiGHmXHjh20atWKKVOmcOedd7Jy5cq6bUOGDOGNN96gvLycqqoqnn/++Ubte+jQobzxxhvs2bOH6upqZs2axeWXX35Cmcsuu4y5c+dy9OhRDh48yAsvvJCQn0tCYtNf4JW7oM8YuHxaw+VFIqRvDT0gsYbP/eEPfwjAWWedxY9//GOGDh1Khw4dOO+8805okmlI586d+elPf8oVV1yBc47Ro0czbtyJ/04PHjyYG2+8kYEDB9KpUyeGDBmS0J9PGuIPnxvEoQ+UwXO3QOF5cN1vNGa5NJqGz22kQ4cO0bp1a6qqqhg/fjy33nor48ePT3kcYThXYVS66yBXPvQmv5o8iDEDu6TuwDXV8Icx8PF78J03oeO5qTu2hMrJhs9VFaCR7r33Xi644AL69+9Pjx49TrhCReSU/fUh2PI3uOYXSuZyytTk0ki6azOz1f7DmtKLXMqWw6L/D/2/CgMnpfDAkmnSroaelrdepxmdowxSVQF/vg3yO8Poh9JwEBkJk7RK6Hl5eezdu1cJ6yScc+zdu5e8vLygQ8loKRs+968Pw+4NcO1DcFq71BxTMlZaNbkUFRVRVlbG7t27gw4lreXl5VFUFKL5LkMkpVWJ3RvhrV9Av+s105AkRFol9JycHHr06BF0GCLJ5xy8cAfktIKrHww6GskQaZXQRYKWsk7RtX+ErW/DmP+E1p2SfDBpLtKqDV2kWag8Cgvv8QaLG/QPQUcjGUQ1dJEYklpBf/vXcGAbXPeoJqqQhFINXSSCS3a36KcfezcR9RkDPS5N7rGk2VFCF0mlN3/mTfY88r6gI5EMpIQuEiGpnaLlW2DlUzD4G9DhnCQcQJo7JXSRVHnzZ2BZcNkPg45EMlRcCd3MRpnZRjMrNbPpMbZ3M7NFZvauma02s2sSH6pIKiW4ir53E6yaBcW3QpsUjuIozUqDCd3MsoFHgKuBvsBkM+sbVewu4Fnn3CBgEvBfiQ5UJBWSNurEGw9Cdku45PtJOoBIfDX0oUCpc+5D59xxYDYQPcmhA9r4y22BHYkLUSTkyjfDmudgyDch/4ygo5EMFk9CPwvYFvG6zF8X6V5gipmVASXAP8fakZlNNbPlZrZc47VIOqq9bDGhnaJv/xosGy66LYE7Ffm8RHWKTgaecM4VAdcAT5nZ5/btnJvhnCt2zhUXFhYm6NAiaezQbnj3KRh4o9rOJeniSejbga4Rr4v8dZG+CTwL4JxbDOQBBYkIUCQICaugL/2tN+b5l76XqD2K1CuehL4M6GVmPcysJV6n57yoMluBEQBm1gcvoatNRUInoZ2iFYdg6e/gvNFQ2DuBOxaJrcGE7pyrAm4HXgbW413NstbM7jOzsX6xHwDfNrP3gFnAzU6zVEhz994sOLYfLlbtXFIjrsG5nHMleJ2dkevujlheB1yc2NBEgmNN7RV1DpbOgC6DoevQxAQl0gDdKSqSDB++Dns+gKFTg45EmhEldJFkWDoDWhVA/+uDjkSaESV0kQh1g3M1ZSflm2HjArjwZmiR2/SgROKkhC6SaMse8wbhKr416EikmVFCF4nQ5DtFK495NxKdNxraRt9QLZJcSugiibRhPhwt98ZtEUkxJXSRRFr5B2h3NnS/LOhIpBlSQheJ0KQZi/Z9BB+9CYOmQJZ+tST19K0TSZRVT3udoRd8LehIpJlSQheJUDtehTX2wsWaanj3aTh3BLQtSnhcIvFQQhdJhNLX4OAObwJokYAooYskwrtPeXeG9h4VdCTSjCmhi0Rwp3Kr6NFy+OAlGDABWrRMSlwi8VBCF2mqdfOg+rg3K5FIgJTQRSJ81inaCKufhYLe0PmCJEQkEj8ldJGm2L8NtvwVBkxM8MzSIo2nhC7SFGue854H3BBsHCIooYuc4LM7ReOobTsHq+dA12HQoUdyAxOJgxK6yKnauQZ2b4DzJwYdiQighC4SxR8+N56iq+dAVg70G5/UiETipYQucipqauD9P0LPK6FVh6CjEQGU0EVOTdky71Z/zRkqaUQJXSRC3MPnrv0TZOfqVn9JK0roIo1VUwPr/uw1t+S1CToakTpK6CIRXMNFoGyp19zS77pkhyPSKEroIjGcdDz0tXPV3CJpSQldpDFqamDdXOg1Us0tknaU0EUiNNgpWrYUDn4MfdXcIulHCV2kMWqvbvmCmlsk/Sihi0Som+AiltqrW3qNhNz81AUlEqe4ErqZjTKzjWZWambT6ykz0czWmdlaM3smsWGKpFbMFpdt73jNLbrVX9JUi4YKmFk28AgwEigDlpnZPOfcuogyvYAfARc758rNrFOyAhYJzPoX/KtbvhJ0JCIxxVNDHwqUOuc+dM4dB2YD46LKfBt4xDlXDuCc25XYMEVSo67BJbqK7hxsmA/nDFdzi6SteBL6WcC2iNdl/rpIvYHeZvY3M1tiZjF7jMxsqpktN7Plu3fvPrWIRYLwyVrYvwXOGx10JCL1SlSnaAugFzAcmAz8zszaRRdyzs1wzhU754oLCwsTdGiRFNjwImDwhauDjkSkXvEk9O1A14jXRf66SGXAPOdcpXPuI+ADvAQvEip116FHt7lsmA9dvwit1T0k6SuehL4M6GVmPcysJTAJmBdVZi5e7RwzK8BrgvkwgXGKBGf/Vti5Ws0tkvYaTOjOuSrgduBlYD3wrHNurZndZ2Zj/WIvA3vNbB2wCLjTObc3WUGLJIurnbEosoK+ocR7VkKXNNfgZYsAzrkSoCRq3d0Ryw74F/8hklk2zIfCPtDx3KAjETkp3SkqcjJH9sGWt1U7l1BQQheJVNcp6vvgZXDVSugSCkroIiezYT7kd4Eug4KORKRBSugiEWrvFDUzOH4ESl/zaucNTjIqEjwldJH6fLgIqo6quUVCQwldpD4bXoTcttD9kqAjEYmLErpIhLo7RV0VbFzgjayYnRNsUCJxUkIXiSF/13I4uk/NLRIqSugiEWrvFG23daE39nnPEQFHJBI/JXSRz3G03/qKxj6X0FFCF4nSx7aSe6hMzS0SOkroIhGcg6uyluM09rmEkBK6SJSrspdzuNOFGvtcQkcJXSRCy0Nl9Mvawv5uI4MORaTRlNBFIhSUvQrA/m5XBRyJSOMpoYtEKChbyMaaIira9gg6FJFGU0IXqXVkH213L2NhzYUai0tCSQldpNYHL2GuhperhwQdicgpUUIXqbXhRY6ddgZrnJpbJJyU0EWgbuzzPUUjAUMtLhJGSugiUDf2+Z6iK4OOROSUKaGLQN3Y5/sLhwL+jEUiIaOELlL92djnLktjn0t4KaGLbFtSN/a5q5tVVCR8lNBFNrz4ubHP1eAiYaSELs2bc7BhvsY+l4yghC7N2yfvw/6tdWOf180pqiq6hJASujRvG14EjX0uGUIJXZq3DfOh6xfrxj536hOVEFNCl+arfAvsXBNzqjndKyphpIQuzdfGBd6z5g6VDBFXQjezUWa20cxKzWz6Scp91cycmRUnLkSRJNkwHwr7QMdz61apxUXCrMGEbmbZwCPA1UBfYLKZ9Y1RLh/4HvBOooMUSbgj+2DL2/XWznWVi4RRPDX0oUCpc+5D59xxYDYwLka5+4EHgWMJjE8kOTaWgKv+XEJ36hWVEIsnoZ8FbIt4Xeavq2Nmg4GuzrkXT7YjM5tqZsvNbPnu3bsbHaxIwqz7M7TrBl0GBR2JSMI0uVPUzLKAh4AfNFTWOTfDOVfsnCsuLCxs6qFFTs3R/bBpEfQdp7YVySjxJPTtQNeI10X+ulr5QH/gdTPbDAwD5qljVNLWBy9BTSX0ve5zm9TgImEWT0JfBvQysx5m1hKYBMyr3eicO+CcK3DOdXfOdQeWAGOdc8uTErFIU62dC22K4KwL6y2iiruEUYMJ3TlXBdwOvAysB551zq01s/vMbGyyAxRJqGOfwqbXoO/YmFlbfaISZi3iKeScKwFKotbdXU/Z4U0PSyRJPngZqo977ecnoTtFJYx0p6g0L+vmQn5nKBoadCQiCaeELs1HxSEofRX6jIWs+r76anOR8FJCl+bj769A1bEGm1tAnaISTkro0nysmwund4Juw4KORCQplNCleag4BB+8An3GQFZ2vcU0Y5GEmRK6NA8bS6DqKAyYEHQkIkmjhC7Nw5rnoG1Xb3aik1CXqISZErpkvsN7oPQ16P/Vk1zdciJdhy5hpIQumW/dXG+oXDW3SIZTQpfMt+Z/vJmJzujXYFF1ikqYKaFLZtu/FbYuhgE3KEtLxlNCl8z2/vPe84Ab4iru1C0qIaaELplt9XPeuC3tuzfqbarLSxgpoUvm+vg92LUWzp8YdCQiKaGELpnr3achu6V3uWKcNB66hJkSumSmqgpY8yycNxpadWj029V/KmGkhC6Z6YOX4Gg5XDClUW9TBV3CTAldMtO7T0N+Fzj3ilPcgaroEj5K6JJ5Du6E0oUwcNJJR1YUyTRK6JJ53psNrgYu+Hqj3+rUKyohpoQumaWmBlY+CV2HQUHPU96NOkUljJTQJbN89Abs2wRDvhl0JCIpp4QumWXZTGjVMa55Q09GFXQJIyV0yRyf7oCNC2DQFGiRG3Q0IimnhC6ZY8UfvM7QC2855V2oT1TCTAldMkN1Jaz8A/S8Ejr0aPLuTL2iEkJK6JIZNpbAwY+b3Bmq4XMlzJTQJTMsfsQbIrfXVQnZnernEkZK6BJ+25bCtndg2D/pzlBp1pTQJfze/hXktT2lO0OjqVNUwiyuhG5mo8xso5mVmtn0GNv/xczWmdlqM3vNzM5OfKgiMez7CDbMh+JbIbd1wnarPlEJowYTupllA48AVwN9gclm1jeq2LtAsXPufOB/gJ8lOlCRmJY8CpYNQ7+TkN2phi5hFk8NfShQ6pz70Dl3HJgNnHAbnnNukXPuiP9yCVCU2DBFYji0yxu3ZcAEaNM5obs2dYtKCMWT0M8CtkW8LvPX1eebwIJYG8xsqpktN7Plu3fvjj9KkVje/hVUV8ClPwg6EpG0kNBOUTObAhQDP4+13Tk3wzlX7JwrLiwsTOShpbk5vMcbt6X/DU0aVTGaWlwkzFrEUWY70DXidZG/7gRmdiXwE+By51xFYsITqcfiX0PlUbjszqTsXp2iEkbx1NCXAb3MrIeZtQQmAfMiC5jZIOC3wFjn3K7EhykS4cg+WPo76H89FPZO6K41wYWEWYMJ3TlXBdwOvAysB551zq01s/vMbKxf7OdAa+A5M1tlZvPq2Z1I0731H1B5BC7716AjEUkr8TS54JwrAUqi1t0dsXxlguMSia18Myyd4d1E1Om8oKMRSSu6U1TC5S8PeNedX/HjpOxeDS4SZkroEh7bV8Ka5+Ci26BNl6QeSp2iEkZK6BIOzsHLP4FWBXDx95J4nOTtWiTZ4mpDFwnce7Nh69sw5peQ1yboaETSkmrokv6O7INX7oKioTDoH1JySM1YJGGkGrqkv7/cD0f3wbVzISu5dRDNWCRhphq6pLetS2D54/DFf4QzB6TssKqfSxgpoUv6qjgEf/oOtOuWtMsUo+lGUQkzNblI+nrlLijfAreUQG5+0NGIpD3V0CU9/X0hrHgcvvTPcPaXUn549YlKGCmhS/rZvw3+OBU69YMrfpLSQ6vFRcJMCV3SS1UFPHcT1FTBxCchJy+QMDRjkYSR2tAlvbz0I9i+Am7874ROXBEvdYpKmKmGLunjnd/C8sfgS/8H+owJOhqR0FFCl/Sw/gVYMA3OuxauvDfoaNQpKqGkhC7B27IYnv8WFBXDV2dCVnZgoehOUQkzJXQJ1tYl8PQN0LYIJs+GnNOCjkgktJTQJThbl8B/fxXyz4Sb5sPpBUFHVEctLhJGSugSjI0L4KnxnyXzNp2DjgjQVS4SbkroknpLfwezvwaFX4CbS9ImmZ9AVXQJIV2HLqlTeQxemu7d0t/7arjhMWh5etBRnUAVdAkzJXRJjb2bvDtAd66Bi++AEXcHejWLSCZSQpfkqqmBpTPgtX+D7JYweQ58YVTQUTVIt/5LGCmhS/J8sg7m3wHb3oGeI2HMw97lielMvaISYkrokngHd8Ki/wfvPgV5bWH8b+H8G0N1+2WIQhWpo4QuiXNgOyx+xOv0rK70po277E5o1SHoyOKm+rmEmRK6NI1zsGMlLHsMVj8Lrgb6fxWGT4eO5wYdnUizooQup+bgTlj7J1j5FOxaCy1Og+Jb4KLbof3ZQUfXZGpxkTBSQpf4OAd7PoAPXoL186FsGeCgyyAY/RAMuMFrLw859YlKmCmhS2zVVbBno3eFykdvwea/wuFd3rYzz4crfuyNWd6pT7BxJompV1RCSAm9uaupgU+3w95S2LcJdr4PO1fDJ2uh6phXJr8znDMcelzqPbfrFly8SeZURZcQiyuhm9ko4D+BbGCmc+6nUdtzgSeBC4G9wI3Ouc2JDVUaraoCju73atYHd8KnO7zngx97j/ItUP7RZ4kbILctdD4fhnwLOg+ELoO9zk3VWEXSXoMJ3cyygUeAkUAZsMzM5jnn1kUU+yZQ7pzraWaTgAeBG5MRcOg45135UV3pTXxcUwU11f5zZdRr/1Fd+3wcKo9C1VHvufYR/fr4YTi230vedc8HvHKxtOro1brbd4eeI7yE3eFc77nNWUreqFNUwimeGvpQoNQ59yGAmc0GxgGRCX0ccK+//D/Ar83MXBL+f132/MOcuXYG5l8xbDhwDqtdrlvvvT6hXN06wN9mEVceW9066nrHal/X7tsiyhJR/rP9uBOOnU1Nok8BADUYFbSkwnI5Rh6H7HQOWmsOWXsOWRGHslpzKLc1B6015daOvdaBvVkdKLf2VFoOHMV77Izc6yb/0XyVH6kMOgSRUxZPQj8L2Bbxugz4Yn1lnHNVZnYA6AjsiSxkZlOBqQDdup1aO2yLNp34pFXviLQNziJT6okp+8TttesjyxmurjoW/SfAagOPSOcR62vXWew/DWBUWzY1ZFNj2VRbNtX+cg3e6xrLppoW/rO/zV+uthYcz8qj0lpy3PI4nuU9V1ouVZbT6Jp0W/8hJ9el7Wm0a5UTdBgijZbSTlHn3AxgBkBxcfEp1d4HjfwajPxaQuMSEckE8UxwsR3oGvG6yF8Xs4yZtcCrCO5NRIAiIhKfeBL6MqCXmfUws5bAJGBeVJl5wE3+8g3AX5LRfi4iIvVrsMnFbxO/HXgZ77LF3zvn1prZfcBy59w84DHgKTMrBfbhJX0REUmhuNrQnXMlQEnUursjlo8BExIbmoiINIYmiRYRyRBK6CIiGUIJXUQkQyihi4hkCAvq6kIz2w1sOcW3FxB1F2qaUFyNo7gaL11jU1yN05S4znbOFcbaEFhCbwozW+6cKw46jmiKq3EUV+Ola2yKq3GSFZeaXEREMoQSuohIhghrQp8RdAD1UFyNo7gaL11jU1yNk5S4QtmGLiIinxfWGrqIiERRQhcRyRBpm9DNbIKZrTWzGjMrjtr2IzMrNbONZvaVet7fw8ze8cvN8Yf+TXSMc8xslf/YbGar6im32czW+OWWJzqOGMe718y2R8R2TT3lRvnnsNTMpqcgrp+b2QYzW21mfzKzdvWUS8n5aujnN7Nc/zMu9b9L3ZMVS8Qxu5rZIjNb53//vxejzHAzOxDx+d4da19JiO2kn4t5fumfr9VmNjgFMX0h4jysMrNPzeyOqDIpO19m9nsz22Vm70es62BmC83s7/5z+3ree5Nf5u9mdlOsMg1yzqXlA+gDfAF4HSiOWN8XeA/IBXrgTYKZHeP9zwKT/OXfAN9Ncrz/Adxdz7bNQEEKz929wA8bKJPtn7tzgJb+Oe2b5LiuAlr4yw8CDwZ1vuL5+YF/An7jL08C5qTgs9KyUSYAAAQfSURBVOsMDPaX84EPYsQ1HJifqu9TvJ8LcA2wAG9uyGHAOymOLxtvltyzgzpfwGXAYOD9iHU/A6b7y9Njfe+BDsCH/nN7f7l9Y4+ftjV059x659zGGJvGAbOdcxXOuY+AUryJrOuYmQFfxpuwGuAPwHXJitU/3kRgVrKOkQR1k387544DtZN/J41z7hXnXJX/cgne7FdBiefnH4f33QHvuzTC/6yTxjn3sXNupb98EFiPN2dvGIwDnnSeJUA7M+ucwuOPADY55071DvQmc869iTcnRKTI71F9uegrwELn3D7nXDmwEBjV2OOnbUI/iViTVkd/4TsC+yOSR6wyiXQp8Ilz7u/1bHfAK2a2wp8oOxVu9//t/X09/+LFcx6T6Va82lwsqThf8fz8J0x+DtROfp4SfhPPIOCdGJsvMrP3zGyBmfVLUUgNfS5Bf6cmUX+lKojzVesM59zH/vJO4IwYZRJy7lI6SXQ0M3sVODPGpp845/6c6nhiiTPGyZy8dn6Jc267mXUCFprZBv8veVLiAh4F7sf7Bbwfrzno1qYcLxFx1Z4vM/sJUAU8Xc9uEn6+wsbMWgPPA3c45z6N2rwSr1nhkN8/MhfolYKw0vZz8fvIxgI/irE5qPP1Oc45Z2ZJu1Y80ITunLvyFN4Wz6TVe/H+3Wvh16xilUlIjOZNin09cOFJ9rHdf95lZn/C+3e/Sb8I8Z47M/sdMD/GpnjOY8LjMrObgWuBEc5vPIyxj4SfrxgaM/l5maVw8nMzy8FL5k875/4YvT0ywTvnSszsv8yswDmX1EGo4vhckvKditPVwErn3CfRG4I6XxE+MbPOzrmP/SaoXTHKbMdr669VhNd/2ChhbHKZB0zyr0DogfeXdmlkAT9RLMKbsBq8CayTVeO/EtjgnCuLtdHMTjez/NplvI7B92OVTZSodsvx9Rwvnsm/Ex3XKOBfgbHOuSP1lEnV+UrLyc/9NvrHgPXOuYfqKXNmbVu+mQ3F+z1O6h+aOD+XecA3/KtdhgEHIpoakq3e/5KDOF9RIr9H9eWil4GrzKy930R6lb+ucVLR83sqD7xEVAZUAJ8AL0ds+wneFQobgasj1pcAXfzlc/ASfSnwHJCbpDifAP4xal0XoCQijvf8x1q8podkn7ungDXAav/L1Dk6Lv/1NXhXUWxKUVyleO2Eq/zHb6LjSuX5ivXzA/fh/cEByPO/O6X+d+mcFJyjS/CaylZHnKdrgH+s/Z4Bt/vn5j28zuUvpSCumJ9LVFwGPOKfzzVEXJ2W5NhOx0vQbSPWBXK+8P6ofAxU+vnrm3j9Lq8BfwdeBTr4ZYuBmRHvvdX/rpUCt5zK8XXrv4hIhghjk4uIiMSghC4ikiGU0EVEMoQSuohIhlBCFxHJEEroIiIZQgldRCRD/C+U78DWqfeh6gAAAABJRU5ErkJggg==\n","text/plain":["<Figure size 432x288 with 1 Axes>"]},"metadata":{"tags":[],"needs_background":"light"}}]},{"cell_type":"markdown","metadata":{"id":"XASc3eYAm4tY"},"source":["Il sigmoide è una versione 'soft' della step function, però è differenziabile! Questo ci servirà per utilizzare il GD."]},{"cell_type":"markdown","metadata":{"id":"QkhS20qVYp-y"},"source":["It is not enough. Indeed, the perceptron is not flexible. Our model has only one neuron. It is time now, to make it smarter, by adding other neurons 🤯\n","\n","Here is our new architecture:\n","\n","\n","\n","The model is called **Multilayer Perceptron (MLP)** and in our case it is comprised of an **input layer**, an **hidden layer** (commonly called **Fully Connected Layer (FCL)**), and a generic **output layer**.\n","First of all, let's define a generic layer with $n$ neurons.\n","\n","A multi-neuron layer is quite simple to implement:\n","- **input:** $\\vec{x}_i = \\begin{pmatrix}\\vec{x}_0 & \\dots \\vec{x}_m \\end{pmatrix}$ (in our case $m = 2$)\n","- **(hidden) output:** $\\vec{h}_i = \\begin{pmatrix}h_{i0} & \\dots & h_{ik}\\end{pmatrix}$ (in our case we have chosen $k = 2$)\n","- The FCL is composed of $k$ perceptrons $h_{ij}$.\n","- Each of the is equipped with a vector of weights $\\vec{w}_j$. In total, the FCL is associated with a matrix $\\vec{W} \\in \\mathbb{R}^{m \\times k}$.\n","- A perceptron $j$ operates a scalar product + sigmoid $\\sigma(\\vec{x}_i\\vec{w}_j)$. Then, the hidden layer operates a vector-matrix product + sigmoid $\\sigma(\\vec{x}_i\\vec{W})$ (the sigmoid is here applied to each single component of the vector).\n"]},{"cell_type":"code","metadata":{"id":"VN5tMuJldjiY"},"source":["class Layer(nn.Module):\n"," def __init__(self, n_in, n_out, a=None):\n"," super().__init__()\n"," W = torch.rand(n_in, n_out)\n"," b = torch.rand(n_out) # bias parameter\n"," self.W = nn.Parameter(W)\n"," self.b = nn.Parameter(b)\n"," \n"," def forward(self, x):\n"," x = x @ self.W\n"," x = x + self.b\n"," x = torch.sigmoid(x)\n"," return x\n","\n","class MLP(nn.Module):\n"," def __init__(self):\n"," super().__init__()\n"," # Sequential is a container of layer, look what happens in forward!\n"," self.layers = nn.Sequential(Layer(2, 2), # x --> H\n"," Layer(2, 1)) # H --> out\n"," \n"," def forward(self, x):\n"," return self.layers(x).view(-1) # so easyyy!"],"execution_count":null,"outputs":[]},{"cell_type":"markdown","metadata":{"id":"FdxsIWSjolLQ"},"source":["Now, let's illustrate the algorithm of gradient descent. It's similar to the delta rule:\n","\n","1. $e = 0$\n","2. while $e < \\mathcal{E}$\n"," 1. for $\\vec{x}_i \\in \\vec{X}$\n"," 1. $\\hat{y}_i = f(\\vec{x}_i)$\n"," 2. $\\ell(y_i, \\hat{y}_i) = \\frac{1}{2}(\\hat{y}_i - y_i)^2$\n"," 2. $E(f) = \\frac{1}{n}\\sum_{i = 1}^n \\ell(y_i, \\hat{y}_i)$\n"," 3. for $j \\in \\{0, \\dots, m\\}$\n"," 1. $w_j^{(e + 1)} = w_j^{(e)} - \\eta \\nabla_\\vec{w}{E(f)}$\n"," 4. $e = e + 1$\n","\n","- $\\ell$ is called **loss function**, there exist many types and that proposed here is called **quadratic loss**.\n","- $E(f)$ is the '**expected loss** (or **empirical risk**). It is simply the average of the lesses computed over all the dataset. The greater is its value, the worse are our predictions. Our aim consists on minimizing it, by bringing it to $0$. It's often called \"loss\" only, generating some ambiguity with the previous term. Since we like ambiguity, we we'll use the term \"loss\". If used in combination with the quadratic loss, it's also called **Mean Squared Error (MSE)** loss\n","- $\\nabla_\\vec{w}{E(f)}$ is the gradient, that is a vector containing the derivatives of $E(f)$ for all the $w_j$. We don't compute it manually, PyTorch takes care of it 🌟\n","\n"]},{"cell_type":"code","metadata":{"id":"vY4A8a6V7bXe"},"source":["def GD(X, y_true, p, epochs=1, eta=0.5, device='cpu'):\n"," X, y_true = X.to(device), y_true.to(device)\n"," \n"," y_pred = p(X).round()\n"," prog_bar = tqdm(range(epochs), total=epochs,\n"," desc=f'E:(), ACC: {evaluate(y_true, y_pred)}')\n"," for e in prog_bar:\n"," p.train() # switch the gradient to training mode: start gradient tracking\n"," l = torch.zeros(len(y_true), device=device)\n","\n"," for i, (x, y) in enumerate(zip(X, y_true)):\n"," y_hat = p(x).view([]) # forward step (change out shape to [] if needed)\n"," l[i] += 0.5 * (y_hat - y) ** 2. # compute the loss\n","\n"," E = l.mean() # compute the (expected) loss\n"," E.backward() # backpropagation: compute the gradient\n","\n"," with torch.no_grad(): # without it, the weights can't be modified\n"," for param in p.parameters(): # weight updates\n"," param -= eta * param.grad\n"," p.zero_grad() # remember to zero out the gradients!\n"," p.eval() # switch the model to evaluation mode: no more gradient tracking\n","\n"," y_pred = p(X).round() # predict based on the sigmoid values\n"," prog_bar.set_description(f'E: {E.item():.4f}, '\n"," f'ACC: {evaluate(y_true, y_pred)}%')"],"execution_count":null,"outputs":[]},{"cell_type":"markdown","metadata":{"id":"fHZKLOh2il1V"},"source":["Let's run the Gradient Descent and let's see if the accuracy improves"]},{"cell_type":"code","metadata":{"id":"BYF9hlYHlZJm","colab":{"base_uri":"https://localhost:8080/","height":122,"referenced_widgets":["860ff1214beb4c21aa649faeb8e810d1","355e90d9e3634d18aaaf9906566fb4ca","892b8d98ed084d90916663c0ecb489e8","b336ef71bdde4b209ab078ed3588ad97","fcf13191a4db47478aaf2d57a1025725","51efa94a8eae4152b924941a84ec184d","d42b681bc7d8424fbf9e40732cca98a1","f47d9e1dffd747569f514c14e36e2b19"]},"executionInfo":{"status":"ok","timestamp":1590665931499,"user_tz":-120,"elapsed":232802,"user":{"displayName":"Alessandro TORCINOVICH","photoUrl":"https://lh3.googleusercontent.com/a-/AOh14Gi96E7HK6ff0uWSudqbJvEMactRTPtsT5-4448y=s64","userId":"03260776184459049943"}},"outputId":"873dedd2-4908-44c9-eea3-e9c996fdea5a"},"source":["mlp = MLP().to(device)\n","GD(Xor, yor_true, mlp, epochs=2000, eta=.5, device=device)"],"execution_count":null,"outputs":[{"output_type":"stream","text":["/usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:6: TqdmDeprecationWarning: This function will be removed in tqdm==5.0.0\n","Please use `tqdm.notebook.tqdm` instead of `tqdm.tqdm_notebook`\n"," \n"],"name":"stderr"},{"output_type":"display_data","data":{"application/vnd.jupyter.widget-view+json":{"model_id":"860ff1214beb4c21aa649faeb8e810d1","version_minor":0,"version_major":2},"text/plain":["HBox(children=(FloatProgress(value=0.0, description='E:(), ACC: 50.0', max=2000.0, style=ProgressStyle(descrip…"]},"metadata":{"tags":[]}},{"output_type":"stream","text":["\n"],"name":"stdout"}]},{"cell_type":"code","metadata":{"id":"1NUEvajYJ46f"},"source":["fig, axes = plt.subplots(nrows=1, ncols=2)\n","axes = axes.ravel()\n","\n","tmp = Xor.to(device)\n","axes[0].scatter(tmp[:, 0].to('cpu').detach(),\n"," tmp[:, 1].to('cpu').detach(),\n"," c=yor_true)\n","tmp = mlp.layers[0](tmp)\n","axes[1].scatter(tmp[:, 0].to('cpu').detach(),\n"," tmp[:, 1].to('cpu').detach(),\n"," c=yor_true)\n","\n","W, b = mlp.layers[1].W, mlp.layers[1].b\n","m, q = (-W[1] / W[0]).item(), (b / W[0]).item()\n","px = np.array([0., 1.])\n","py = m * px + q\n","axes[1].plot(px, py)\n","plt.show()\n"],"execution_count":null,"outputs":[]},{"cell_type":"markdown","metadata":{"id":"5TtzX2X7uvZ9"},"source":["# ✌️"]}]}