blocksets

A python package for performing set operations on layouts of discrete space in any dimension.

• Block : an orthogonal clump of unit pixels (i.e. a line segment, rectangle, cuboid, hyper... you get the idea)

• BlockSet : takes a composition of the space and resolves it into a disjoint set of Blocks in a consistent fashion.

Why?

You might choose to use a BlockSet instead of a set of tuples because the resolution/granularity is sufficiently high to warrant it.

Or in other words, the number of units being modelled pushes the limits of the available computing power due to the expanse of the space they take up.

How?

• Create any layout (as a blockset) using a stacked list of block operations which add, remove or toggle blocks over the current blockset state.
• Perform the usual set arithmetic union, intersection, difference etc. on blockset objects.
• Compare 2 blockset objects using the standard set comparison methods and operators.
• Results are always consistent regardless of how they were constructed.

Installation

blocksets is available on pypi.org and can be installed using pip (there are no dependent packages).

pip install blocksets

Usage

Visit readthedocs

Review and run the example_use.py module via python -m blocksets.example_use for a few examples, one of which follows here.

TL;DR

from blocksets import Block, BlockSet

# A block is defined by the co-ordinates of the opposite corners
big_rubik = Block((0, 0, 0), (99999, 99999, 99999)) 
assert big_rubik.measure == 999970000299999

# A single argument is a unit block
centre_cube = Block((49999, 49999, 49999))
assert centre_cube.measure == 1

# Create a large 3 dimensional cube with the centre missing
bs = BlockSet(3)  
bs.add(big_rubik)
bs.remove(centre_cube)

assert bs.measure == 999970000299998
assert len(bs) == 6

sorted_blocks = sorted(bs, key=lambda x: x.norm)

for blk in sorted_blocks:
    print(f"{blk:50} {blk.measure}")

The resulting space is modelled using 6 objects (effectively tuples) instead of 999970000299998

(0, 0, 0)..(49999, 99999, 99999)                   499980000249999
(49999, 0, 0)..(50000, 49999, 99999)               4999850001
(49999, 49999, 0)..(50000, 50000, 49999)           49999
(49999, 49999, 50000)..(50000, 50000, 99999)       49999
(49999, 50000, 0)..(50000, 99999, 99999)           4999850001
(50000, 0, 0)..(99999, 99999, 99999)               499980000249999    

Visualisation

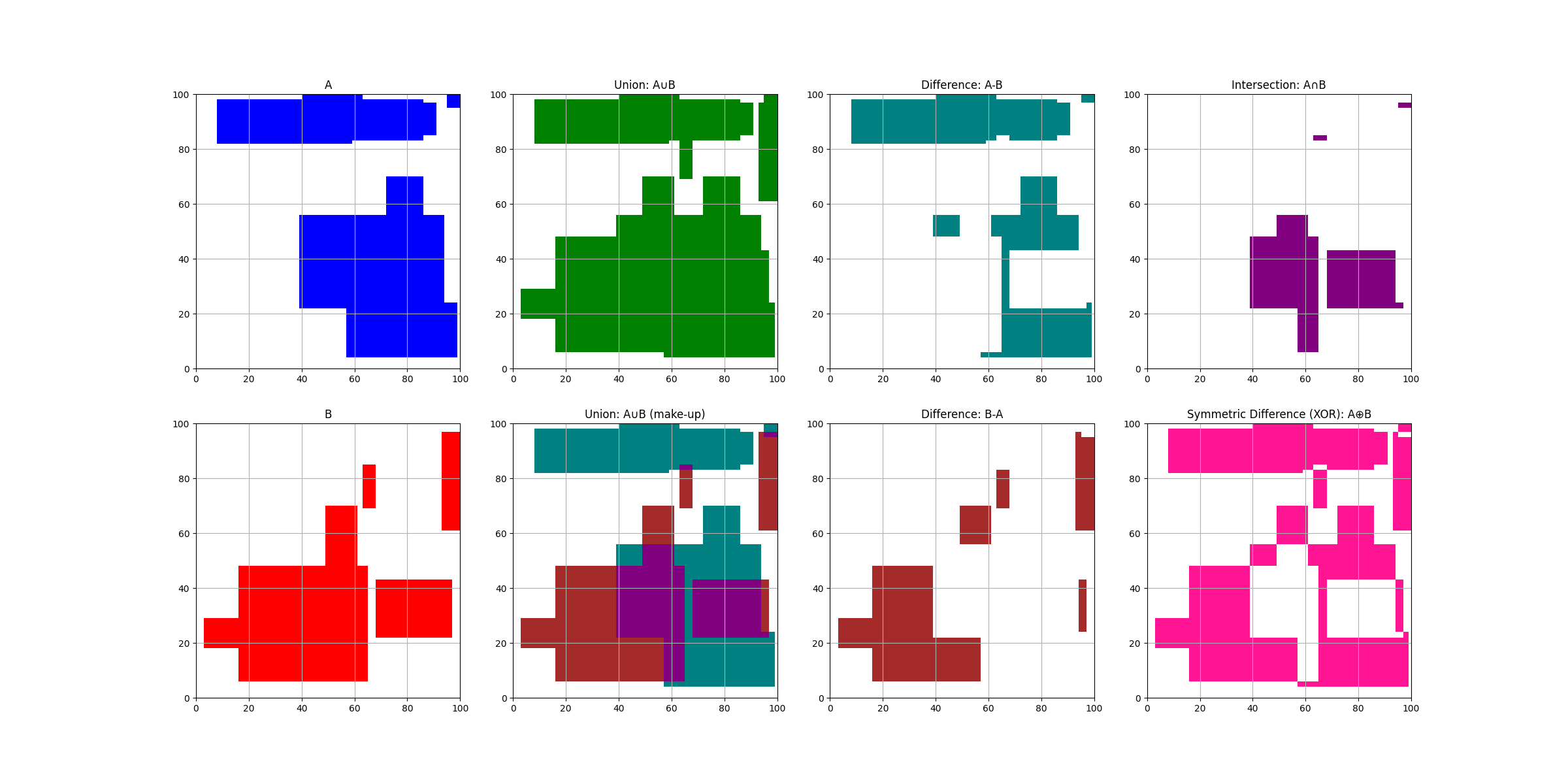
An example of 2D set operations on some randomly generated block sets A, B and drawn using matplotlib.

See readthedocs for the code snippet to generate this.

Contribution

At the moment it is early days so whilst the foundations are forming I am only inviting comments which can be given via github issues