-
Notifications
You must be signed in to change notification settings - Fork 163
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
binseg not expected/optimal speed for best case data #245
Comments
|
Hi, indeed using Dynp(model="l2") results in a O(log(T^3)) complexity where T is the number of samples. The fastest way to detect mean-shifts is to use KernelCPD(kernel="linear"). It follows this article and is coded in C. The complexity is quadratic in number of operations and linear in memory. See here for a comparison between the Python implementation and the C implementation. |
|
Hi, You can try the following cost function which implements CostL2 with pre-computed cumsum signals. Hopefully, it will show the expected/optimal log-linear time complexity. The following code defines the cost function. from ruptures.costs import NotEnoughPoints
from ruptures.base import BaseCost
import numpy as np
from numpy.linalg import norm
class CostL2CumSum(BaseCost):
r"""
Least squared deviation.
For two indexes $a<b$, the cost function on the sub-signal
$y_{a..b} = [y_a, y_{a+1},\dots,y_{b-1}]$, is equal to
$$
c(y_{a..b}) = \sum_{t=a}^{b-1} \|y_t - \bar{y}_{a..b}\|^2
$$
where $\bar{y}_{a..b}$ is the empirical mean of $y_{a..b}$.
For efficiency, the cost function is re-written with the cumulative sums of
the signals $y$ and $[\|y_1\|^2, \|y_2\|^2,\dots,\|y_T\|^2]$.
"""
model = "l2_cumsum"
def __init__(self):
"""Initialize the object."""
self.signal = None
self.signal_cumsum = None
self.signal_norm_cumsum = None
self.min_size = 1
def fit(self, signal) -> "CostL2":
"""Set parameters of the instance.
Args:
signal (array): array of shape (n_samples,) or (n_samples, n_features)
Returns:
self
"""
if signal.ndim == 1:
self.signal = signal.reshape(-1, 1)
else:
self.signal = signal
self.signal_cumsum = np.cumsum(self.signal, axis=0)
self.signal_norm_cumsum = np.cumsum(norm(self.signal, axis=1) ** 2, axis=0)
return self
def error(self, start, end) -> float:
"""Return the approximation cost on the segment [start:end].
Args:
start (int): start of the segment
end (int): end of the segment
Returns:
segment cost (float): the value of the cost on the segment [start:end]
Raises:
NotEnoughPoints: when the segment is too short (less than `min_size`
samples).
"""
if end - start < self.min_size:
raise NotEnoughPoints
if start == 0:
res = self.signal_norm_cumsum[end - 1] - norm(
self.signal_cumsum[end - 1]
) ** 2 / (end - start)
return res
res = (
self.signal_norm_cumsum[end - 1]
- self.signal_norm_cumsum[start - 1]
- norm(self.signal_cumsum[end - 1] - self.signal_cumsum[start - 1]) ** 2
/ (end - start)
)
return resTo use it with Binseg algo = rpt.Binseg(custom_cost=CostL2CumSum(), jump=1, min_size=1).fit(signal)
algo.predict(n_bkps=10) |
|
We will not change the current implementation of CostL2 because, for small signals (below 1000 samples approx.), the naive implementation is faster. Hope this helps |
|
Closing for now, feel free to reopen. |
Hum, I fear that for such long signals, the cumsum vectors quickly overflow but that is only an assumption. To cope with this, they should be replaced by cumulative average. If that still interests you, I can provide the associated cost function. |
I do not know why to be honest. Is the number of changes fixed? |
|
No the number of changes is not fixed. In the experiment https://github.com/tdhock/binseg-model-selection/blob/main/figure-timings-data.R I used max.segs <- as.integer(N.data/2)
max.changes <- max.segs-1Lso it should be log-linear in N.data in the best case. |


related to benchmarks #231
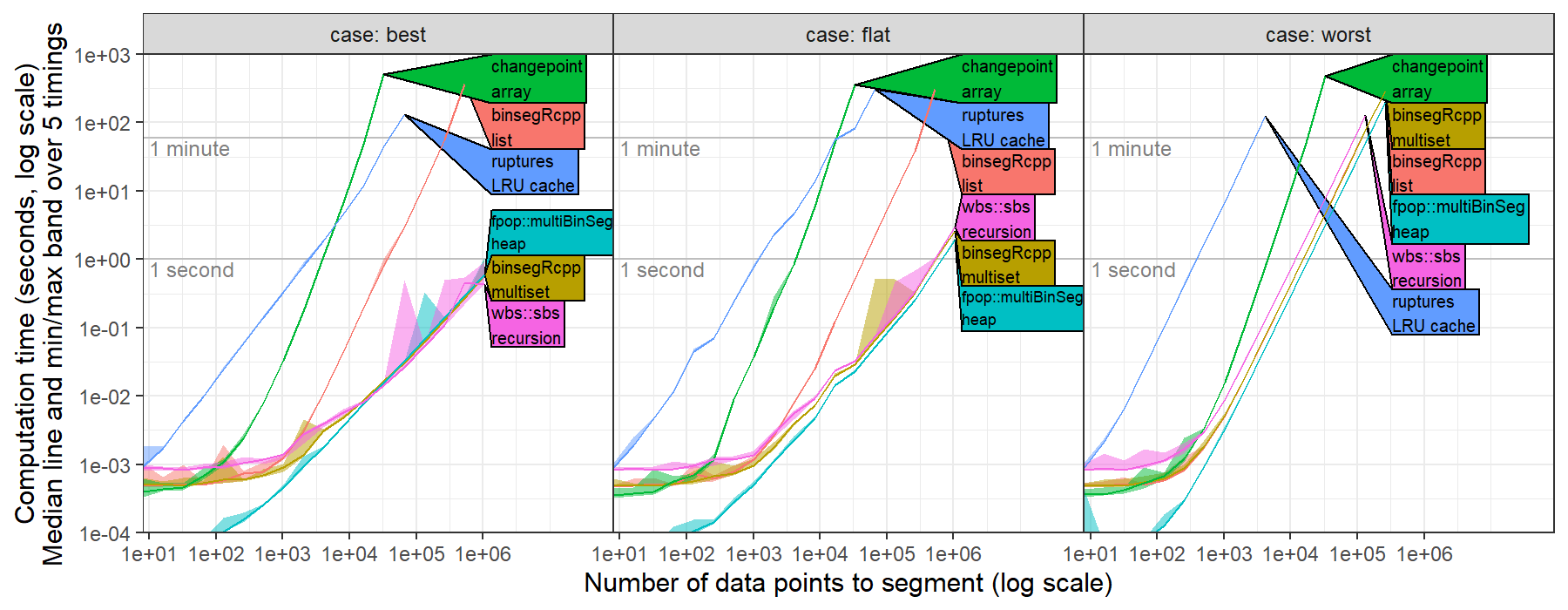
I recently computed timings for ruptures.Binseg using the l2 model (normal change in mean, square loss) for univariate data, https://github.com/tdhock/binseg-model-selection#22-mar-2022
For worst case data, ruptures shows the expected/optimal quadratic time complexity.
For best case data, ruptures was slower than the expected/optimal log-linear time complexity.
This is probably because the time complexity of CostL2.error(start,end) is linear in number of data, O(end-start).
Could probably be fixed by computing cumsum vectors in fit method, then using them to implement a constant O(1) time error method.
The text was updated successfully, but these errors were encountered: