Перевод статьи Elyx0: Neural networks from scratch for Javascript linguists (Part1 — The Perceptron).
Существует большая вероятность, что за последние месяцы вы хотя бы раз слышали о нейронной сети или искусственном интеллекте, которые, как представляется, творят чудеса: оценка вашего селфи, SIRI, понимающая ваш голос, победа над человеком в таких играх, как Шахматы и Го, превращение лошади в зебру на произвольной картинке или нейросеть, делающая вас моложе, старше или меняющая ваш пол на любом фото.
От частого использования словосочетания «Искусственный Интеллект» в разных контекстах само понятие стало настолько размытым, что оно в лучшем случае коррелирует с «чем-то, что выглядит умным».
Возможно, из-за такой путаницы машинное обучение кажется слишком сложным для понимания, типа: «Готов поспорить, столько математики - не для меня!».
Не парьтесь, у меня та же история, так что давайте отправимся в путешествие. Я расскажу вам все, что узнал, мои заблуждения, способ правильно интерпретировать результаты и некоторые основные словарные и интересные факты на этом пути.
Представьте себе коробку, в которой вы вырезаете несколько отверстий и размещаете предопределенное количество чисел 0 или 1. Затем коробка бурно вибрирует и выдает из каждого отверстия одно число: 0 или 1. Отлично.
Изначально ваша коробка тупая, как картон: она не выдаст ожидаемый результат магическим образом. Вы должны обучить её достижению желаемой цели.
Моя самая большая ошибка - попытка осилить концепции, просто глядя на верхушку айсберга, играя с библиотеками и бомбить, когда ничего не работает. При попытке понять нейронные сети это непозволительно.
Изобретение этого магического термина датируется около 1943 года, когда 45-летний нейрофизиолог Уоррен Стургис Мак-Каллок и его коллега Уолтер Питтс написали статью под названием «Логическое исчисление идей, присущих нервной деятельности».
По примеру классических философов Греции, Мак-Каллок попытался математически смоделировать работу мозга.
Это была яркая идея, учитывая то, как долго на тот момент было известно о существовании нейрона (примерно с 1900-х годов) и что электрическая природа их сигналов будет продемонстрирована только в конце 1950-х годов.
Давайте здесь остановимся и вспомним, что опубликованные статьи не означают, что написавший их человек был абсолютно прав. Это означало: у парня была гипотеза, он знал кое что в этой области, имел какие-то результаты (иногда неприменимые) и опубликовал это. Затем другие квалифицированные люди из этой области должны воспроизвести результаты и решить, стоит ли на этом строить новую теорию.
Некоторые научные работы, будучи никем не проверяемы, могут породить аберрации, подобные этой статье 2011 года, в которой говорится, что люди могут видеть будущее.
Тем не менее, теперь мы знаем, что Мак-Каллок был нормальным парнем и в своей статье он попытался смоделировать некоторые алгоритмы физического мозга, лежащие в основе нервной системы (которой обладает большинство многоклеточных животных), являющейся на самом деле сетью нейронов.
Надеюсь, читая дальше, вы не потеряете слишком много таких штук (источник)
Человеческий мозг имеет ~86 миллиардов нейронов, каждый из которых имеет аксоны, дендриты и синапсы, соединяющие каждый нейрон с ~7000 других. Это почти столько же связей, сколько галактик во Вселенной.
Проблема для Мак-Каллока заключалась в том, что в 1943 году экономическая ситуация была не очень оптимистичной: США в состоянии войны, Франклин Д. Рузвельт, чтобы предотвратить инфляцию, заморозил цены и заработную плату, Никола Тесла скончался, а лучшим компьютером был ЭНИАК, который стоил 7 миллионов долларов за 30 тонн (в то время в технике властвовал дикий сексизм, поэтому тот факт, что ЭНИАК был изобретен 6 женщинами, заставил их коллег мужчин ошибочно его недооценивать). Для сравнения: стандартный телефон Samsung 2005 года имел в 1300 раз большую вычислительную мощность, чем ЭНИАК.
Затем в 1958 году компьютеры стали немного лучше и Фрэнк Розенблатт, вдохновленный Мак-Каллоком, подарил нам Перцептрон.
Пока все были заняты развитием этих идей, 11 лет спустя Марвин Мински решил, что ему не нравится эта идея, как и то, что Фрэнк Розенблатт не отстранен от работы. Он объяснился, опубликовав книгу, в которой сказал: «Большинство работ Розенблатта... Не имеют научной ценности...». Влияние этой книги заключается в том, что она истощила и без того низкое финансирование в этой области.
Какие были доводы Мински против падавана Мак-Каллока?
Хотя это понятие может звучать как название серии «Теории Большого Взрыва», оно фактически представляет собой основу теории Минского, призванной отвлечь от оригинального Перцептрона.
Перцептрон Розенблатта очень похож на нашу коробку, в которой на этот раз мы пробурили одно отверстие:
Нейронная сеть на самом деле может принимать на вход значения между 0 и 1
Если сумма наших входных сигналов (x1...x4), умноженная на их весовые коэффициенты (w1...w4) плюс смещение (b), достаточна для того, чтобы заставить результирующий затвор превышать порог (T), наша дверь выдаст значение 1, иначе - 0.
Чтобы это произошло, пороговое значение сравнивается с результатом функции активации. Точно так же, как мозговые нейроны реагируют на стимул. Если раздражитель слишком низок, нейрон не пропускает сигнал вдоль аксона к дендритам.
В общем случае в коде это выглядит так:
// Инициализируем входные сигналы
const x1 = 1;
const x2 = 0.3;
const x3 = 0.2;
const x4 = 0.5;
// Инициализируем весовые коэффициенты
const w1 = 1.5;
const w2 = 0.2;
const w3 = 1.1;
const w4 = 1.05;
const Threshold = 1;
const bias = 0.3;
// Значение, вычисляемое для сравнения с пороговым, - сумма
// произведений входных значений
// (1*1.5)+(.3*0.2)+(.2*1.1)+(.5*1.05)
const sumInputsWeights = x1*w1 + x2*w2 + x3*w3 + x4*w4; // 2.305
const doorWillOpen = activation(sumInputsWeights + bias) > Threshold; // trueВ организме человека ток нейрона в спокойном состоянии составляет -70 мВ, а его порог активации -55 мВ. В случае оригинального Перцептрона эта активация обрабатывается ступенчатой функцией Хевисайда.
0, если x отрицательный, 1 - если нет. X является суммой входных весов и смещения
Одной из наиболее известных функций активации является сигмоидальная функция: F (x) = 1 / (1 + exp (-x)) и сдвиг (bias) обычно используется для смещения порога активации:
Изменение функции активации может привести к большей вариативности результатов при срабатывании нейронов
Некоторые функции активации могут давать отрицательные значения, а некоторые - нет. Это будет иметь важное значение при использовании результатов функции активации одного перцептрона для подачи в качестве входов другого перцептрона.
Использование 0 в качестве входного сигнала исключает связанный с ним вес из конечной суммы.
Таким образом, вместо наличия возможности получения отрицательного веса, 0 действует как деактиватор. Тогда как нам может потребоваться этот вес для инверсии значимости входа в итоговой сумме.
Существуют различные функции активации
Перцептрон известен как бинарный классификатор. Это означает, что он может классифицировать только 2 класса (спам или не спам, апельсин или не апельсин... и так далее).
Его также можно назвать линейный классификатор. Его цель состоит в том, чтобы определить, к какому классу принадлежит объект в соответствии со своими характеристиками (или «функциями»: наши x1-x4), производя итерации до тех пор, пока не будет найдена линия, которая правильно отделяет объекты разных классов друг от друга.
Мы даем нашему классификатору некоторые примеры ожидаемых результатов, учитывая некоторые исходные данные, и он тренируется на поиск этого разделения путём регулировки сдвига и весов на каждом вводе.
В качестве примера давайте с использованием перцептрона классифицируем некоторые сущности по принципу «опасен или нет» в соответствии с двумя характеристиками: количество зубов и размер.
В зависимости от случая кошка может быть не того класса, что ожидается
Теперь, когда мы натренировали наш перцептрон, мы можем классифицировать образцы, которых он никогда не видел:
Здесь живая демка. Нет, серьезно, зацените. (прим. пер.: здесь исходный код с переводом интерфейса.)
То, в чем Минский упрекал Розенблатта, состояло примерно в следующем: что, если вдруг мой тренировочный набор содержал гигантскую змею, почти не имеющую зубов, но большую, как слон.
Тренировочный набор бывает невозможно разделить одной линией
Теперь требуется две линии, чтобы правильно отделить красные объекты от зеленых. При использовании одного перцептрона, эта невозможность заставит его приспосабливаться вечно, будучи неспособным разделить входные данные на классы одной прямой.
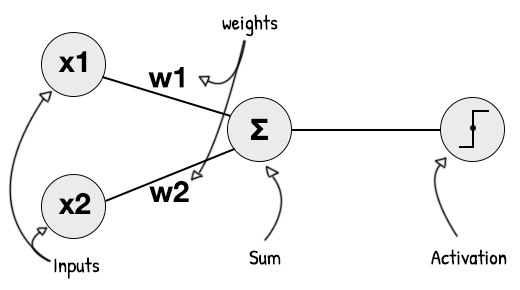
Вы уже, должно быть, понимаете обычное представление перцептрона:
Сдвиг (bias) может применяться либо после вычисления суммы, либо в качестве добавленного веса для мнимого ввода, всегда равного 1
Один из способов - просто обучить два перцептрона: один ответственный за верхнее левое разделение, другой - за нижнее правое. Подключая их вместе через логическое «и», мы создаём некий мультиклассовый перцептрон.
const p1 = new Perceptron();
p1.train(trainingSetTopLeft);
p1.learn(); // P1 готов.
const p2 = new Perceptron();
p2.train(trainingSetBottomRight);
p2.learn(); // P2 готов.
const inputs = [x1,x2];
const result = p1.predict(inputs) & p2.predict(inputs);
Существуют и другие способы решения этой проблемы, которые мы рассмотрим в части 2
Операция «логическое И», обозначаемая A^B, - одна из логических операций, которые может выполнять перцептрон. Полагая w5 и w6 равными примерно 0,6 и применяя смещение -1 к нашей сумме, мы действительно создали предиктор AND.
Помните, что входы, связанные с w5 и w6, поступают от активации ступенчатой функции Heaviside, которая даёт только 0 или 1 в качестве выхода.
Для 0 & 0 : (0*0.6 + 0*0.6)-1 меньше 0, Вывод: 0
Для 0 & 1 : (0*0.6 + 1*0.6)-1 меньше 0, Вывод: 0
Для 1 & 1 : (1*0.6 + 1*0.6)-1 больше 0, Вывод: 1
Выполняя эту цепочку и имея «удлиненный» наш первоначальный перцептрон, мы создали так называемый скрытый слой, который в основном представляет собой несколько нейронов, вставленных между исходными входами и конечным выходом.
На самом деле их следует называть «слоями детекторов признаков» или «слоями подпроцессов»
Хуже всего то, что Минский все это знал и решил сосредоточиться на простейшей версии перцептрона, чтобы дискредитировать все работы Розенблатта. Розенблатт уже рассмотрел многослойный и перекрестно-связанный перцептрон в своей книге «Принципы нейродинамики: перцептроны и теория механизмов мозга» в 1962 году.
Все это подобно публикации книги про транзисторы, в которой непризнание компьютера мотивируется тем, что обособленный транзистор бесполезен.
Вы все должны быть знакомы со следующими уравнениями: y = f(x), Y = mx + c или y = ax + b.
Итак, как мы получаем эти m и c из нашего тренированного перцептрона?
Чтобы понять это, мы должны вспомнить исходное уравнение нашего перцептрона: x1 * w1 + x2 * w2 + bias > T.
Смещение (bias) и порог (threshold) - это одинаковые понятия, а для перцептрона T = 0, что означает, что уравнение принимает вид:
x1 * w1 + x2 * w2 > -bias, что можно переписать как:
X2 > (-w1 / w2) * x1 + (-bias / w2), сравнивая это с:
Y = m * x + b, мы можем видеть, что
Y это x2,
X это x1,
M это (-w1 / w2) и b это (-bias / w2).
Это означает, что градиент (m) нашей линии определяется двумя весами, а точка пересечения прямой и вертикальной оси определяется сдвигом (bias) и вторым весом.
Теперь мы можем просто выбрать два значения x (0 и 1), заменить их в линейном уравнении и найти соответствующие значения y, а затем проследить линию между двумя точками (0; f(0)) и (1; f(1)).
Подобно оцепленному месту преступления, имея доступ к уравнению, мы можем включить дедукцию:
y = (-w1/w2)x + (-bias/w2)
- Градиент (угол поворота) линии зависит только от двух весов
- Знак минус перед
w1означает, что если оба веса имеют один и тот же знак, линия будет наклонена вниз, как\, а если они отличаются друг от друга, она будет направлена вверх/ - Регулировка w1 будет влиять на угол поворота, но не на координату точки пересечения с вертикальной осью, вместе с тем w2 будет влиять и на угол поворота и на координату точки пересечения
- Поскольку сдвиг (bias) - это числитель (верхняя половина фракции), его увеличение поднимает линию выше по оси. (точка пересечения с вертикальной осью будет выше)
Вы можете проверить окончательные веса в демо, введя в консоли app.perceptron.weights.
И это именно то, что наш перцептрон пытается оптимизировать, пока не найдет правильную линию.
Я знаю, это может выглядеть как 2 линии, но это одна, движущаяся супер быстро
Очевидно, наш перцептрон не может угадать вслепую и пробует каждое значение для своих весов, пока не найдет линию, правильно разделяющую сущности. Мы должны применять правило дельты.
Это правило обучения для обновления весов, связанных с входами в однослойной нейронной сети. Оно имеет следующее представление:
Не беспокойтесь, это может быть «упрощено» следующим образом:
Мы делаем это для каждого вхождения в тренировочном наборе
Сопоставление ожидаемое - фактическое показывает значение ошибки (или стоимость). Цель состоит в том, чтобы пройти через тренировочный набор и уменьшить эту ошибку/стоимость до минимума, добавляя или вычитая небольшое количество весов каждого входа до тех пор, пока не совпадут с ответами все ожидания тренировочного набора.
Если после некоторых итераций ошибка равна 0 для каждого элемента в наборе тренировок, наш перцептрон обучен, и наше линейное уравнение, использующее эти конечные веса, правильно разделяет входящие наборы на классы.
В приведенном выше уравнении α представляет собой константу: скорость обучения, которая будет влиять на то, как изменяется каждый вес.
- Если α слишком мала, для поиска правильных весов потребуется больше итераций и вы можете попасть в локальные минимумы.
- Если α слишком велика, обучение может никогда не найти правильных весов.
Один из способов увидеть это - вообразить бедного парня в железных сапогах, связанных вместе, который хочет достичь сокровища на дне скалы, но он может двигаться только прыжком на α метров:
Одна вещь, которую вы, возможно, захотите сделать при чтении статьи в Википедии, - это перейти в раздел «Обсуждение», в котором обсуждаются спорные области содержимого.
В случае дельта-формулы в содержании говорилось, что она не может быть применена к перцептрону, потому что у функции Хевисайда не существует производной в точке 0, но в разделе «Разговор» приведены статьи преподавателей MIT, использующих её.
Собрав воедино все, что мы узнали, мы, наконец, кодим перцептрон:
// Полная версия: https://github.com/Elyx0/rosenblattperceptronjs/blob/master/src/Perceptron.js
class Perceptron {
constructor(bias=1,learningRate=0.1,weights=[]) {
this.bias = bias;
this.learningRate = learningRate;
this.weights = weights;
this.trainingSet = [];
}
init(inputs,bias=this.bias) {
// Инициализируем веса случайными значениями и добавляем сдвиговый вес
this.weights = [...inputs.map(i => Math.random()), bias];
}
adjustWeights(inputs,expected) {
const actual = this.evaluate(inputs);
if (actual == expected) return true; // Если ошибки нет, возвращаем ничего не трогая
// В противном случае корректируем веса, добавляя error * learningRate относительно очередного
this.weights = this.weights.map((w,i) => w += this.delta(actual, expected,inputs[i]));
}
// Вычисляем разницу между выводом и ожиданием для текущего ввода
delta(actual, expected, input,learningRate=this.learningRate) {
const error = expected - actual; // Насколько мы ошиблись
return error * learningRate * input;
}
// Сумма inputs * weights
weightedSum(inputs=this.inputs,weights=this.weights) {
return inputs.map((inp,i) => inp * weights[i]).reduce((x,y) => x+y,0);
}
// Вычисляем результат с текущими весами
evaluate(inputs) {
return this.activate(this.weightedSum(inputs));
}
// Heaviside в качестве функции активации
activate(value) {
return value >= 0 ? 1 : 0;
}
}Кроме того, Перцептрон относится к категории нейронных сетей прямого распространения, которая является просто причудливой формулировкой, говорящей о том, что связи между элементами сети не образуют цикл.
В чем была некоторая правота Мински: при том что алгоритм перцептрона гарантированно сходится на каком-либо решении в случае линейно разделяемого обучающего набора, он все равно может выбрать любое допустимое решение, а некоторые проблемы могут допускать множество решений различного качества.
Ваш мозг делает почти то же самое. Как только он найдет правильный способ взаимодействовать с мышцей (например: мышца реагирует сокращением), он будет использовать этот способ и далее. Эти связи «мозг-мышца» для всех разные.
Интеллектуалы любят спорить друг с другом, как Мински и Розенблатт. Даже Эйнштейн оказался неправ в своей борьбе против Нильса Бора по вопросу квантового индетерминизма, утверждая своей знаменитой цитатой: «Бог не играет в кости».
Мы закончим поэтическими строками от отца нейронных сетей Уоррена Мак-Каллока (он действительно был поэтом).
Надеюсь, вы кое-чему научились, и я скоро увижу вас в Части 2.
Our knowledge of the world, including ourselves,
is incomplete as to space and indefinite as to time.
This ignorance, implicit in all our brains,
is the counterpart of the abstraction which renders our knowledge useful.
Слушайте наш подкаст в iTunes и SoundCloud, читайте нас на Medium, контрибьютьте на GitHub, общайтесь в группе Telegram, следите в Twitter и канале Telegram, рекомендуйте в VK и Facebook.