如果树中的每一个节点最多只能由两个子节点,这样的树就称为二叉树;
- 二叉树可以为空,也就是没有节点;
- 若二叉树不为空,则它由根节点和称为其左子树 TL 和右子树 TR 的两个不相交的二叉树组成;
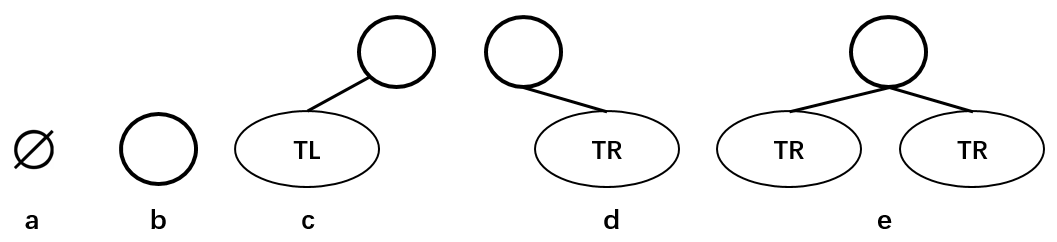
上图分别表示:空的二叉树、只有一个节点的二叉树、只有左子树 TL 的二叉树、只有右子树 TR 的二叉树和有左右两个子树的二叉树。
- 一个二叉树的第 i 层的最大节点树为:2^(i-1)^,i >= 1;
- 深度为 k 的二叉树的最大节点总数为:2^k^ - 1 ,k >= 1;
- 对任何非空二叉树,若 n
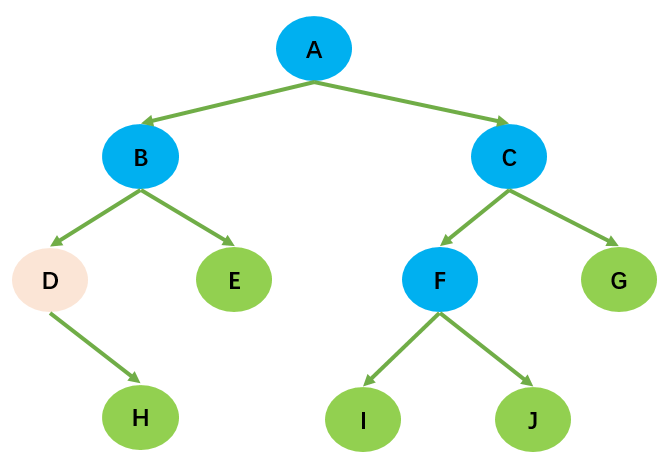
0表示叶子节点的个数,n2表示度为 2 的非叶子节点个数,那么两者满足关系:n0= n2+ 1;如下图所示:H,E,I,J,G 为叶子节点,总数为 5;A,B,C,F 为度为 2 的非叶子节点,总数为 4;满足 n0= n2+ 1 的规律。
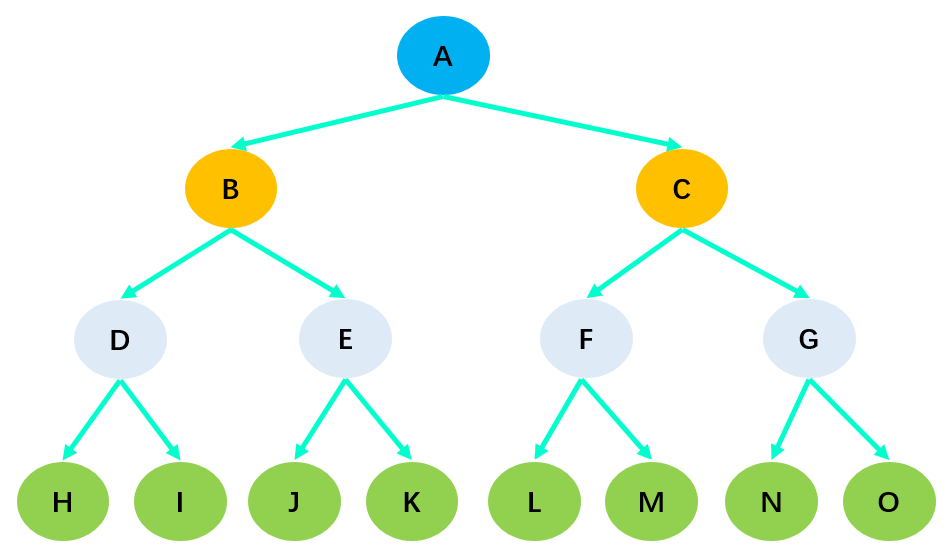
完美二叉树(Perfect Binary Tree)也成为满二叉树(Full Binary Tree),在二叉树中,除了最下一层的叶子节点外,每层节点都有 2 个子节点,这就构成了完美二叉树。
完全二叉树(Complete Binary Tree):
- 除了二叉树最后一层外,其他各层的节点数都达到了最大值;
- 并且,最后一层的叶子节点从左向右是连续存在,只缺失右侧若干叶子节点;
- 完美二叉树是特殊的完全二叉树;
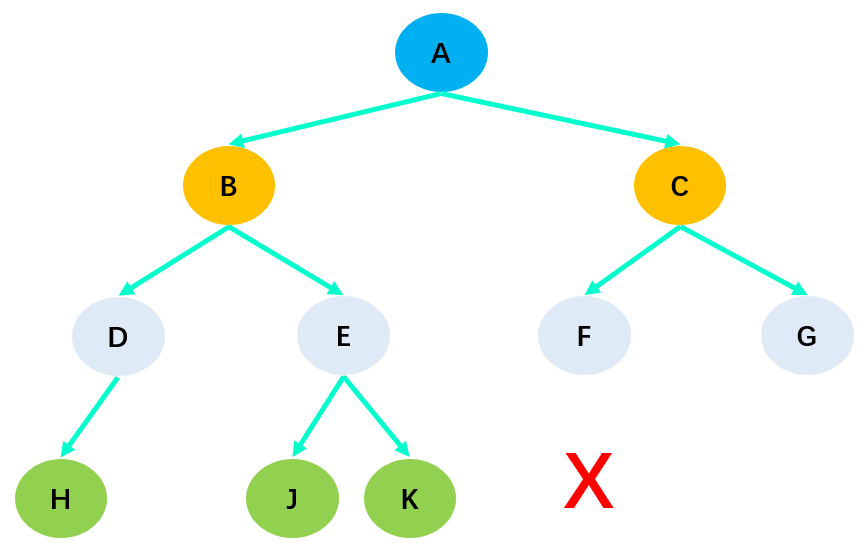
在上图中,由于 H 缺失了右子节点,所以它不是完全二叉树。
常见的二叉树存储方式为数组和链表:
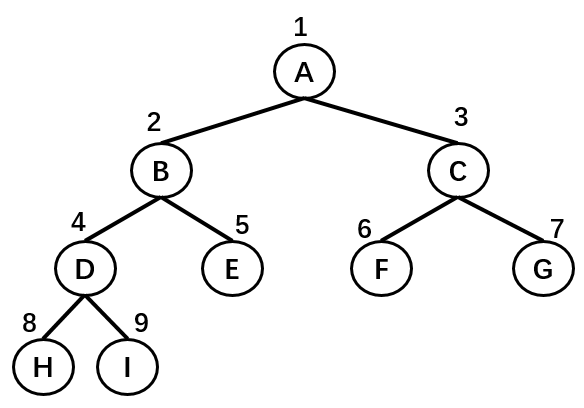
- 完全二叉树:按从上到下,从左到右的方式存储数据。
| 节点 | A | B | C | D | E | F | G | H | I |
|---|---|---|---|---|---|---|---|---|---|
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
使用数组存储时,取数据的时候也十分方便:左子节点的序号等于父节点序号 _ 2,右子节点的序号等于父节点序号 _ 2 + 1 。
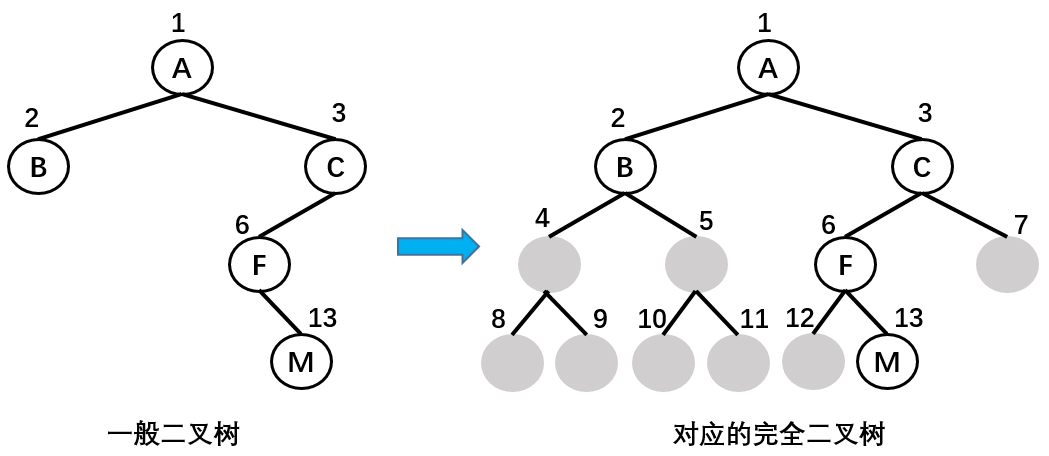
- 非完全二叉树:非完全二叉树需要转换成完全二叉树才能按照上面的方案存储,这样会浪费很大的存储空间。
| 节点 | A | B | C | ^ | ^ | F | ^ | ^ | ^ | ^ | ^ | ^ | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
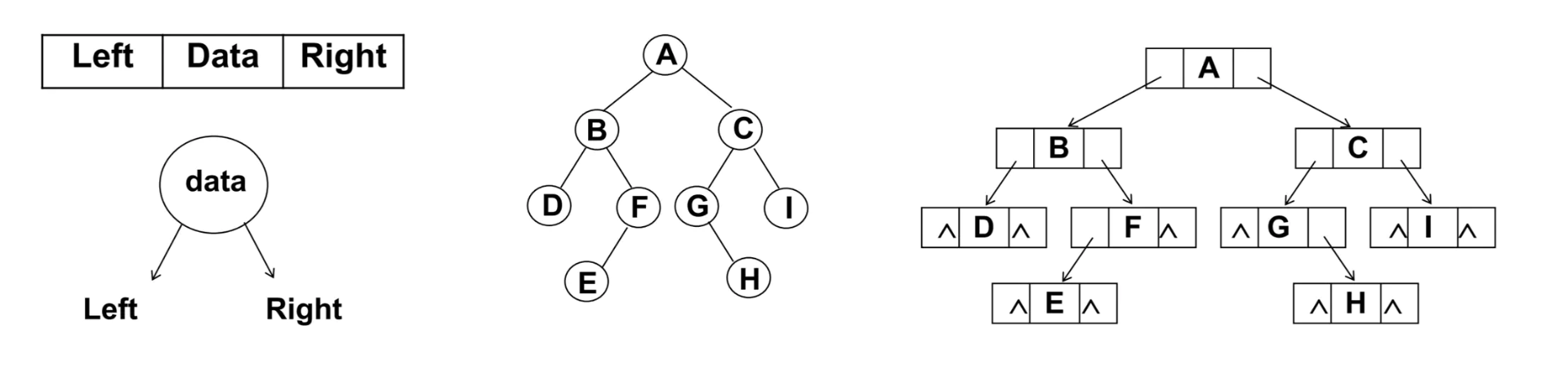
二叉树最常见的存储方式为链表:每一个节点封装成一个 Node,Node 中包含存储的数据、左节点的引用和右节点的引用。