-
Notifications
You must be signed in to change notification settings - Fork 2
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Cutoff for popular/nonpopular based on distribution diagram #68
Comments
|
Thank you for the explanation @hosseinfani Please read the description above @edwinpaul121 |
|
@Hamedloghmani, yes I'd like to have a meeting about this so I can get a better understanding of the task. |
|
@edwinpaul121 , sure. I'll get in touch in MS Teams and schedule a meeting soon. |
|
Hi, I've gotten the 1st part of the problem done. Please verify and let me know if any changes need to be made. import matplotlib.pyplot as plt
import statistics
def plot_distribution(data1,data2):
'''
@args
float list for x axis values
float list for y axis values
'''
# Calculations : mean, std dev, mean + 1 std dev, mean + 3 std dev
mean = statistics.mean(data1)
stdDev = statistics.stdev(data1)
fig, ax = plt.subplots(figsize = (10,6))
# Plots data
ax.scatter(x = data1, y = data2)
# Plotting vertical lines to indicate mean, mean + 1 * stdev and mean + 3 stdev
ax.axvline(mean)
ax.axvline(mean + stdDev)
ax.axvline(mean + (3 * stdDev))
# Titles for x and y axes
plt.xlabel("X-Axis Values")
plt.ylabel("Y-Axis Values")
# Adding grid to display
plt.grid()
# Displays graph
plt.show()2 test cases for the above function : |
|
Thanks a lot for the implementation and progress report. Thank you |
|
Hi, here's an updated version of the code for the first part. Would we require an option to save the graph for this function as well? import matplotlib.pyplot as plt
import statistics
def plot_distribution(data1 : list, data2 : list, n : int):
"""
Args:
data1: Index of experts
data2: Number of teams
n: number of std dev to plot
"""
# Calculations : mean, std dev, mean + 1 std dev, mean + 3 std dev
mean = statistics.mean(data1)
stdDev = statistics.stdev(data1)
fig, ax = plt.subplots(figsize = (10, 6))
# Plots data
ax.scatter(x = data1, y = data2)
# Plotting vertical line to indicate mean
ax.axvline(mean)
# Plotting vertical lines for mean + n * stdev
for i in range(1, n + 1):
ax.axvline(mean + i * stdDev)
# Titles for x and y axes
plt.xlabel("X-Axis Values")
plt.ylabel("Y-Axis Values")
# Adding grid to display
plt.grid()
# Displays graph
plt.show() |
|
Hello @edwinpaul121 Thanks |
|
Hi, updating on some of the issues that I am facing right now,
Here is the code with a few sample runs (The red lines show the interpolated plot) : import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate
def area_under_curve(data_x : list, data_y : list):
"""
Args:
data1: Index of experts
data2: # of teams
"""
fig, ax = plt.subplots(figsize = (10,6))
#------------------------------------------------------------------------------------------------------------------------------------------------
# To plot a line graph of the data, interpolation can be used which creates a function based on the data points
f = interpolate.interp1d(data_x, data_y, kind='linear')
xnew = np.arange(min(data_x), max(data_x), 0.1) # returns evenly spaced values from the data set
ynew = f(xnew)
ax.plot(xnew, ynew, color = 'red')
# the new x and y values could be used separately and we can continue with its own plot, however it does not show the exact values in the graph,
# rather just gives a good idea of how the data set can be interpreted
#------------------------------------------------------------------------------------------------------------------------------------------------
# Find the index of the midpoint of the curve
total_area = np.trapz(data_y, data_x)
half_area = total_area / 2
cum_area = np.cumsum(data_y)
mid_index = np.searchsorted(cum_area, half_area)
#mid_index = len(data_x) // 2
#mid_index = (max(data_x) - min(data_x)) // 2
# Scatter plot of data
ax.scatter(x = data_x, y = data_y)
ax.plot(data_x, data_y, color = "green", alpha = 0.7) # Joins all points by a line
# Fill left half of the area under the curve in blue
ax.fill_between(data_x[ : mid_index + 1], data_y[ : mid_index + 1], color='blue', alpha=0.5)
# Fill right half of the area under the curve in orange
ax.fill_between(data_x[mid_index : ], data_y[mid_index : ], color='orange', alpha=0.5)
# Titles for x and y axes
plt.xlabel("X-Axis Values (Index of Experts)")
plt.ylabel("Y-Axis Values (# Teams)")
# Adding grid to display
plt.grid()
# Displays graph
plt.show() |
|
Hi @edwinpaul121 |
|
@Hamedloghmani, just a follow up on that update, if the arange step value is changed to a value of 0.001, the graph becomes accurate so the plotted lines work well. So that might be sorted but still working on the other issues. |
|
Hi @Hamedloghmani @hosseinfani, just got done working on all of the issues I mentioned earlier. But here's the final code, it includes 2 functions (one of them being a helper that calculates the midpoint, it can just be integrated as one function if required) : import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate
def area_under_curve(data_x : list, data_y : list):
"""
Args:
data1: Index of experts
data2: # of teams
"""
fig, ax = plt.subplots(figsize = (10,6))
# To plot a line graph of the data, interpolation can be used which creates a function based on the data points
f = interpolate.interp1d(data_x, data_y, kind='linear')
xnew = np.arange(min(data_x), max(data_x), 0.001) # returns evenly spaced values from the data set
ynew = f(xnew)
ax.plot(xnew, ynew, color = 'red')
mid_index = midP_calc(xnew, ynew) # helper function that calculates the mid point of the data set that divides the area equally
# Fill left half of the area under the curve in blue
ax.fill_between(xnew[ : mid_index + 1], ynew[ : mid_index + 1], color='blue', alpha=0.5)
# Fill right half of the area under the curve in orange
ax.fill_between(xnew[mid_index : ], ynew[mid_index : ], color='orange', alpha=0.5)
# Scatter plot of data
ax.scatter(x = data_x, y = data_y)
# Titles for x and y axes
plt.xlabel("X-Axis Values (Index of Experts)")
plt.ylabel("Y-Axis Values (# Teams)")
# Adding grid to display
plt.grid()
# Displays graph
plt.show()This is the helper function : def midP_calc(x : list, y : list):
mid_index = len(x) // 2
# Dividing the area under the curve into 2 halves
left_area = np.trapz(y[ : mid_index + 1], x[ : mid_index + 1])
right_area = np.trapz(y[mid_index : ], x[mid_index : ])
# Finding the mid point that divides it equally
while(left_area != right_area):
if(left_area > right_area):
mid_index -= 1
else:
mid_index += 1
left_area = round(np.trapz(y[ : mid_index + 1], x[ : mid_index + 1]), 3)
right_area = round(np.trapz(y[mid_index : ], x[mid_index : ]), 3)
return mid_indexAnd here's the final output with the same axis values as mentioned earlier: |
|
Hi @edwinpaul121 , |
|
Hi @Hamedloghmani, just got done refining the previous code a little bit. I've changed the helper function that calculates the mid point to binary search from linear so I think that should help with the run time a bit. I've done a few tests but I'm not sure how it might affect different systems with different configurations, in mine however there seems to be a noticeable decrease in run time. import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate
def area_under_curve(data_x: list, data_y: list, xlabel: str, ylabel: str, lcolor='green', rcolor='orange'):
"""
Args:
data1: Index of experts
data2: # of teams
xlabel: label for x axis
ylabel: label for y axis
"""
fig, ax = plt.subplots(figsize = (10,6))
# To plot a line graph of the data, interpolation can be used which creates a function based on the data points
f = interpolate.interp1d(data_x, data_y, kind='linear')
xnew = np.arange(min(data_x), max(data_x), 0.001) # returns evenly spaced values from the data set
ynew = f(xnew)
ax.plot(xnew, ynew, color = 'red')
mid_index = mid_calc(xnew, ynew) # helper function that calculates the mid point of the data set that divides the area equally
# Fill left half of the area under the curve in blue
ax.fill_between(xnew[ : mid_index + 1], ynew[ : mid_index + 1], color=lcolor, alpha=0.3)
# Fill right half of the area under the curve in orange
ax.fill_between(xnew[mid_index : ], ynew[mid_index : ], color=rcolor, alpha=0.5)
# Scatter plot of data
ax.scatter(x = data_x, y = data_y)
# Titles for x and y axes
plt.xlabel(xlabel)
plt.ylabel(ylabel)
# Appearance settings
ax.grid(True, color="#93a1a1", alpha=0.3)
ax.minorticks_off()
ax.xaxis.get_label().set_size(12)
ax.yaxis.get_label().set_size(12)
plt.legend(fontsize='small')
ax.set_facecolor('whitesmoke')
# Displays graph
plt.show()Along with the updated helper function : def mid_calc(x : np.ndarray, y : np.ndarray)->int:
"""
Helper function that calculates the middle point of the data set that divides the area equally
Args:
x: values of the x-axis
y: values of the y-axis
Returns:
mid_index: index of the middle point
"""
# Creating a start and end point for binary search
start = 0
end = len(x) - 1
mid_index = (start + end) // 2
# Dividing the area under the curve into 2 halves
left_area = round(np.trapz(y[ : mid_index + 1], x[ : mid_index + 1]), 3)
right_area = round(np.trapz(y[mid_index : ], x[mid_index : ]), 3)
# Finding the middle point that divides it equally
while(left_area != right_area and start <= end):
if (left_area > right_area):
end = mid_index
elif (right_area > left_area):
start = mid_index + 1
else:
return mid_index
mid_index = (start + end) // 2
left_area = round(np.trapz(y[ : mid_index + 1], x[ : mid_index + 1]), 3)
right_area = round(np.trapz(y[mid_index : ], x[mid_index : ]), 3)
return mid_index |
|
I've also updated the code to display mean and std. dev. to now show the mean with a dashed line: import matplotlib.pyplot as plt
import statistics
def plot_distribution(data1 : list, data2 : list, n : int):
"""
Args:
data1: Index of experts
data2: Number of teams
n: number of std dev to plot
"""
# Calculations : mean, std dev, mean + 1 std dev, mean + 3 std dev
mean = statistics.mean(data1)
stdDev = statistics.stdev(data1)
fig, ax = plt.subplots(figsize = (10, 6))
# Plots data
ax.scatter(x = data1, y = data2)
# Plotting vertical line to indicate mean
ax.axvline(mean, linewidth = 1.5, linestyle = "--", color = 'red')
# Plotting vertical lines for mean + n * stdev
for i in range(1, n + 1):
ax.axvline(mean + i * stdDev)
# Titles for x and y axes
plt.xlabel("X-Axis Values")
plt.ylabel("Y-Axis Values")
# Adding grid to display
plt.grid()
# Displays graph
plt.show() |
|
Hi @edwinpaul121 , thank you so much for the update. Thanks |
|
Fixed a line in the mid_calc function that caused issues when running actual data through it. while(abs(left_area - right_area) > 0.05 and start <= end): |








We need to justify the threshold of being popular vs. nonpopular based on distribution of experts.
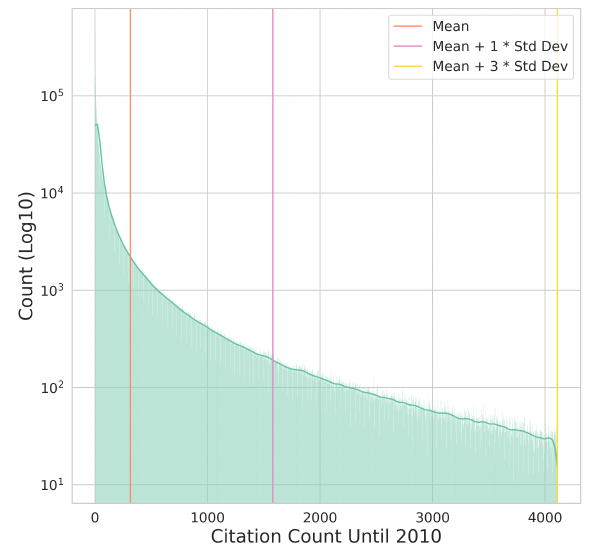
1- We need a figure that shows the distribution and draw the lines on it to show the mean, mean+1std, mean+2std, ... with the value annotated on the lines. Something like this:
2- We need another figure that shows the area under the curve of distribution and split that area into two equal size, annotating each area with the same number. Something like this.

Hopefully, the mean and the area of splited under the carve are close.
@Hamedloghmani @edwinpaul121
How about this issue as the next task for Edwin?
The text was updated successfully, but these errors were encountered: