我们给出了一个(轴对齐的)矩形列表 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐标,(x2,y2)是该矩形右上角的坐标。
找出平面中所有矩形叠加覆盖后的总面积。 由于答案可能太大,请返回它对 10 ^ 9 + 7 取模的结果。
示例 1:
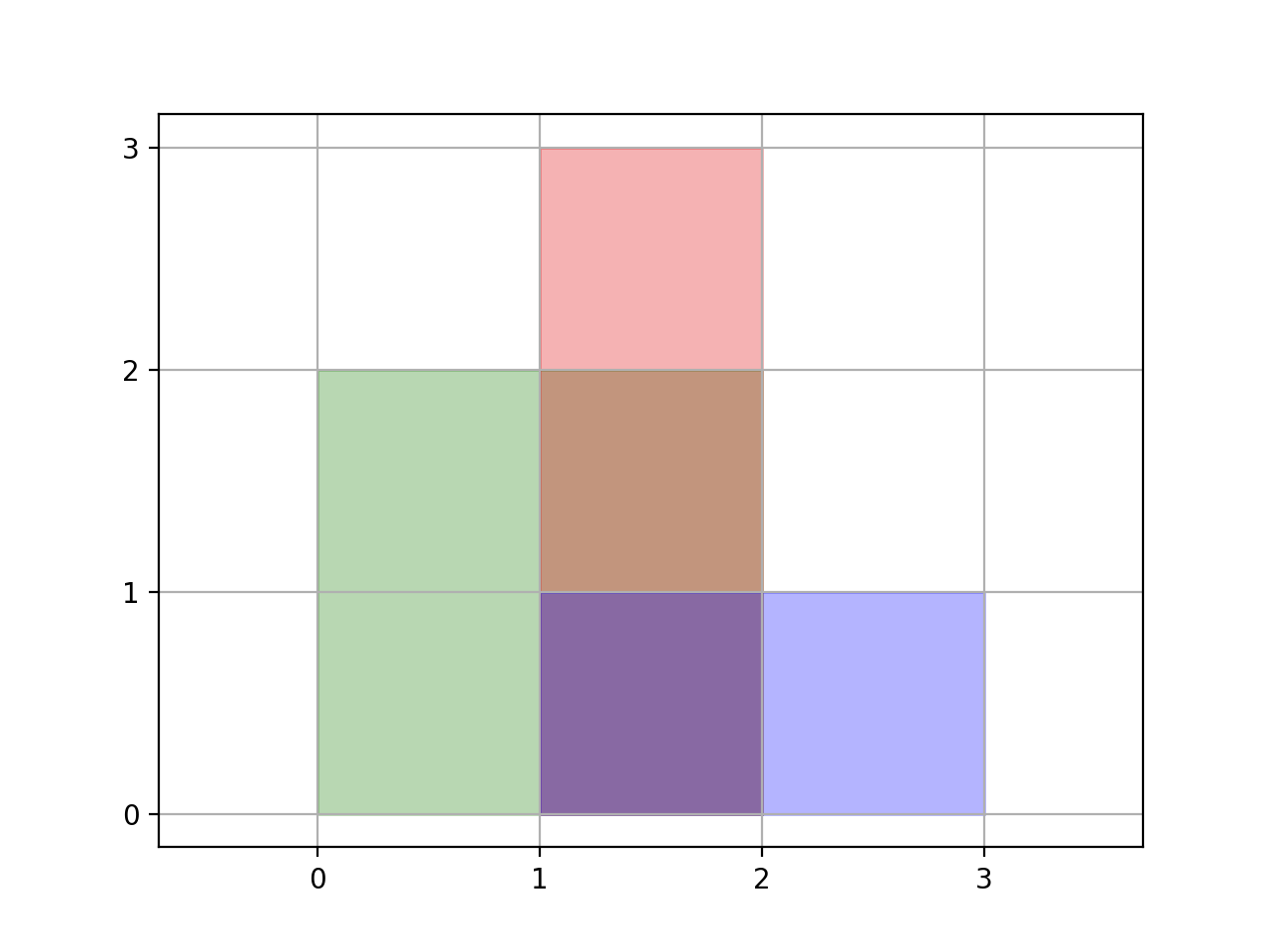
输入:[[0,0,2,2],[1,0,2,3],[1,0,3,1]] 输出:6 解释:如图所示。
示例 2:
输入:[[0,0,1000000000,1000000000]] 输出:49 解释:答案是 10^18 对 (10^9 + 7) 取模的结果, 即 (10^9)^2 → (-7)^2 = 49 。
提示:
1 <= rectangles.length <= 200rectanges[i].length = 40 <= rectangles[i][j] <= 10^9- 矩形叠加覆盖后的总面积不会超越
2^63 - 1,这意味着可以用一个 64 位有符号整数来保存面积结果。