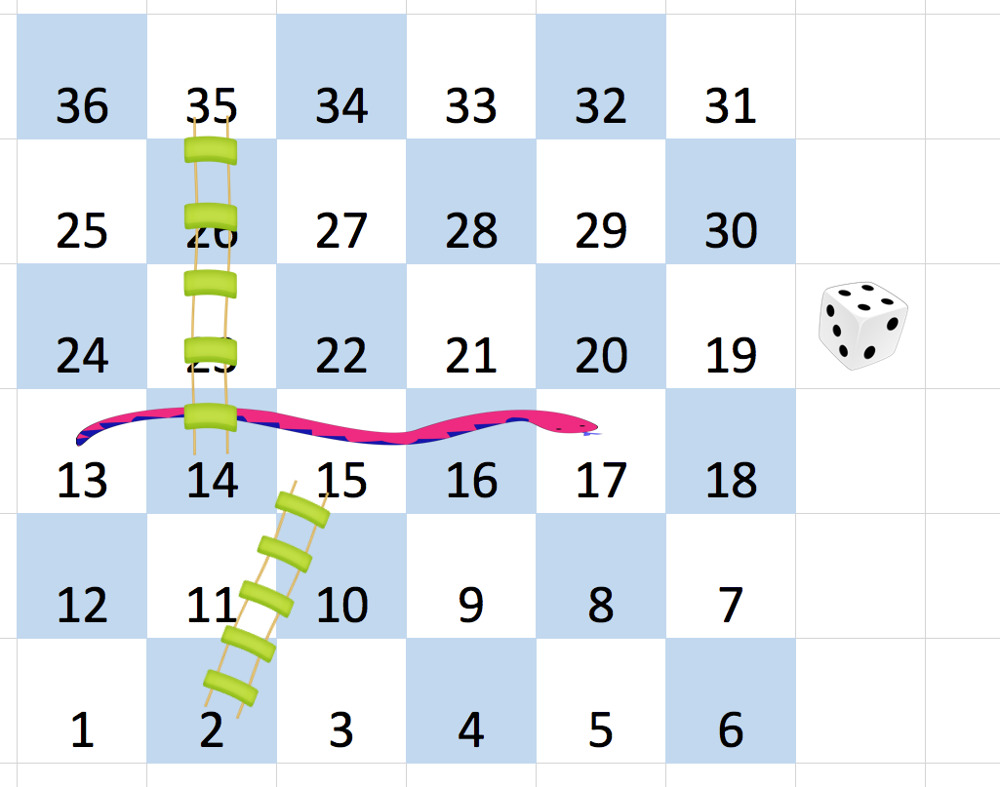
在一块 N x N 的棋盘 board 上,从棋盘的左下角开始,每一行交替方向,按从 1 到 N*N 的数字给方格编号。例如,对于一块 6 x 6 大小的棋盘,可以编号如下:
玩家从棋盘上的方格 1 (总是在最后一行、第一列)开始出发。
每一次从方格 x 起始的移动都由以下部分组成:
- 你选择一个目标方块
S,它的编号是x+1,x+2,x+3,x+4,x+5,或者x+6,只要这个数字<= N*N。 - 如果
S有一个蛇或梯子,你就移动到那个蛇或梯子的目的地。否则,你会移动到S。
在 r 行 c 列上的方格里有 “蛇” 或 “梯子”;如果 board[r][c] != -1,那个蛇或梯子的目的地将会是 board[r][c]。
注意,你每次移动最多只能爬过蛇或梯子一次:就算目的地是另一条蛇或梯子的起点,你也不会继续移动。
返回达到方格 N*N 所需的最少移动次数,如果不可能,则返回 -1。
示例:
输入:[ [-1,-1,-1,-1,-1,-1], [-1,-1,-1,-1,-1,-1], [-1,-1,-1,-1,-1,-1], [-1,35,-1,-1,13,-1], [-1,-1,-1,-1,-1,-1], [-1,15,-1,-1,-1,-1]] 输出:4 解释: 首先,从方格 1 [第 5 行,第 0 列] 开始。 你决定移动到方格 2,并必须爬过梯子移动到到方格 15。 然后你决定移动到方格 17 [第 3 行,第 5 列],必须爬过蛇到方格 13。 然后你决定移动到方格 14,且必须通过梯子移动到方格 35。 然后你决定移动到方格 36, 游戏结束。 可以证明你需要至少 4 次移动才能到达第 N*N 个方格,所以答案是 4。
提示:
2 <= board.length = board[0].length <= 20board[i][j]介于1和N*N之间或者等于-1。- 编号为
1的方格上没有蛇或梯子。 - 编号为
N*N的方格上没有蛇或梯子。