二叉树上有 n 个节点,按从 0 到 n - 1 编号,其中节点 i 的两个子节点分别是 leftChild[i] 和 rightChild[i]。
只有 所有 节点能够形成且 只 形成 一颗 有效的二叉树时,返回 true;否则返回 false。
如果节点 i 没有左子节点,那么 leftChild[i] 就等于 -1。右子节点也符合该规则。
注意:节点没有值,本问题中仅仅使用节点编号。
示例 1:
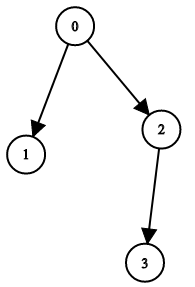
输入:n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1] 输出:true
示例 2:
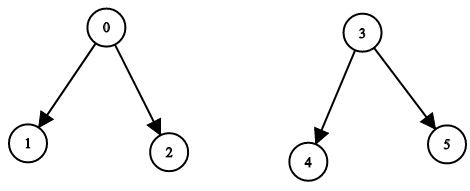
输入:n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1] 输出:false
示例 3:
输入:n = 2, leftChild = [1,0], rightChild = [-1,-1] 输出:false
示例 4:
输入:n = 6, leftChild = [1,-1,-1,4,-1,-1], rightChild = [2,-1,-1,5,-1,-1] 输出:false
提示:
1 <= n <= 10^4leftChild.length == rightChild.length == n-1 <= leftChild[i], rightChild[i] <= n - 1