当模型是多层感知机时,对抗模型框架是最直接应用的。为了学习生成器关于数据 $x$ 上的分布 $p_g$,我们定义输入噪声的先验变量 $p_z(z)$,然后使用 $G(z;\theta_g)$ 来代表数据空间的映射。这里 $G$ 是一个由含有参数 $\theta_g$ 的多层感知机表示的可微函数。我们再定义了一个多层感知机 $D(x;\theta_d)$ 用来输出一个单独的标量。$D(x)$ 代表 $x$ 来自于真实数据分布而不是 $p_g$ 的概率,我们训练 $D$ 来最大化分配正确标签给不管是来自于训练样例还是 $G$ 生成的样例的概率。我们同时训练 $G$ 来最小化 $log(1-D(G(z)))$。换句话说,$D$ 和 $G$ 的训练是关于值函数 $V(G,D)$ 的极小化极大的二人博弈问题。
$$\min_G\max_DV(D,G)=\mathbb{E_{x\sim p_{data}(x)}}[logD(x)]+\mathbb{E_{z\sim p_z(z)}}[log(1-D(G(z)))]\tag{1}$$
在下一节中,我们提出了对抗网络的理论分析,基本上表明基于训练准则可以恢复数据生成分布,因为 $G$ 和 $D$ 被给予足够的容量,即在非参数极限。如图 1 展示了该方法的一个非正式却更加直观的解释。实际上,我们必须使用迭代数值方法来实现这个过程。在训练的内部循环中优化 $D$ 到完成的计算是禁止的。并且有限的数据集将导致过拟合。相反,我们在优化 $D$ 的 k 个步骤和优化 $G$ 的一个步骤之间交替。只要 $G$ 变化足够慢,可以保证 $D$ 保持在其最佳解附近。该过程如算法 1 所示。
实际上,方程 1 可能无法为 G 提供足够的梯度来学习。训练初期,当 G 的生成效果很差时,$D$ 会以高置信度来拒绝生成样本,因为它们与训练数据明显不同。因此,$log(1-D(G(z)))$ 饱和。因此我们选择最大化 $logD(G(z))$ 而不是最小化 $log(1-D(G(z)))$ 来训练 $G$,该目标函数使 $G$ 和 $D$ 的动力学稳定点相同,并且在训练初期,该目标函数可以提供更强大的梯度。
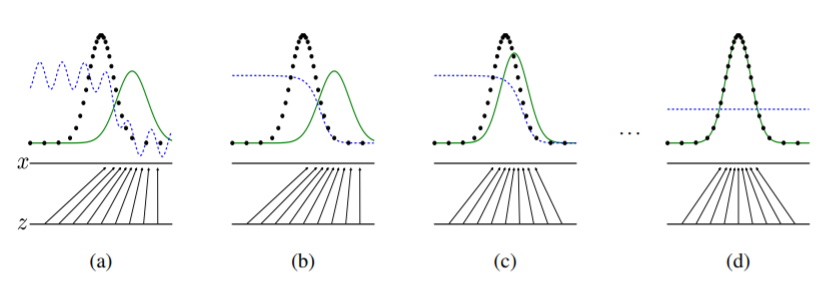
图1. 生成网络在被训练的同时,更新判别分布模型($D$,蓝色虚线)使 $D$ 能区分训练数据分布 $p_x$(黑色虚线)中的样本和生成分布 $p_g$($G$,绿色分布)中的样本。下面的水平线为均匀采样 $z$ 的区域,上面的水平线为 $x$ 的部分区域。朝上的箭头显示映射 $x=G(z)$ 如何将非均匀分布 $p_g$ 作用在转换后的样本上。$G$ 在 $p_g$ 高密度区域收缩,且在 $p_g$ 的低密度区域扩散。(a) 考虑一个接近收敛的对抗模型对:$p_g$ 与 $p_{data}$ 相似,且 $D$ 是个部分准确的分类器。(b) 算法的内循环中,训练 $D$ 来判别数据中的样本,收敛到:$D^*(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$。(c) 在 $G$ 的 1 次更新后,$D$ 的梯度引导 $G(z)$ 流向更可能分类为数据的区域。(d) 训练若干步后,如果 $G$ 和 $D$ 的性能足够,它们接近某个稳定点并都无法继续提高性能,因为此时 $p_g=p_{data}$。判别器将无法区分训练数据分布和生成数据分布,即 $D(x)=\frac{1}{2}$。
算法 1. 生成对抗网络的 minibatch 随机梯度下降训练。判别器的训练步数,$k$,是一个超参数。在我们的试验中使用 $k=1$,使消耗最小。

详情请看:Generative adversarial nets

