There are n cities connected by m flights. Each fight starts from city u and arrives at v with a price w.
Now given all the cities and fights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.
Example 1:
Input:
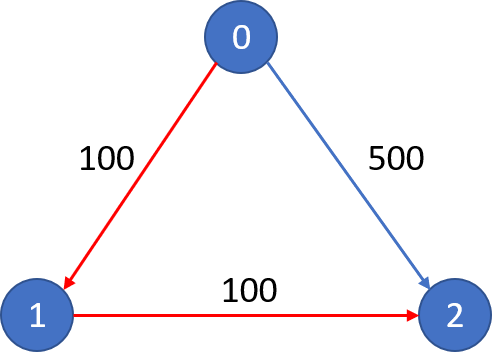
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
Output: 200
Explanation:
The graph looks like this:
The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.
Example 2:
Input:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
Output: 500
Explanation:
The graph looks like this:
The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.
Note:
- The number of nodes n will be in range [1, 100], with nodes labeled from 0 to n - 1.
- The size of flights will be in range [0, n * (n - 1) / 2].
- The format of each flight will be (src, dst, price).
- The price of each flight will be in the range [1, 10000].
- k is in the range of [0, n - 1].
- There will not be any duplicated flights or self cycles.
见程序注释