Property (d) shows that point addition is commutative. The flag is the name we give groups with a commutative operation.
Flag: crypto{ABELIAN}For all the challenges in the starter set, we will be working with the elliptic curve
E: Y^2 = X^3 + 497 X + 1768, p: 9739Using the above curve, and the point P(8045,6936), find the point Q(x, y) such that P + Q = O.
Giữ nguyên x và lấy nghịch đảo y (-y mod p), ta sẽ thu được điểm cần tìm
Flag: crypto{8045, 2803}Using the above curve, and the points P = (493, 5564), Q = (1539, 4742), R = (4403,5202), find the point S(x,y) = P + P + Q + R by implementing the above algorithm.
Làm từng bước theo phương pháp đã được nêu ra trong challenge, nhưng thay vì phép chia ta sẽ dùng modular inverse
vd: (y2 - y1) / (x2 - x1) → ((y2-y1) * inverse(x2-x1, p))
from Crypto.Util.number import*
a = 497
b = 1768
p = 9739
'''
(a) If P = O, then P + Q = Q.
(b) Otherwise, if Q = O, then P + Q = P.
(c) Otherwise, write P = (x1, y1) and Q = (x2, y2).
(d) If x1 = x2 and y1 = - y2, then P + Q = O.
(e) Otherwise:
(e1) if P ≠ Q: λ = (y2 - y1) / (x2 - x1)
(e2) if P = Q: λ = (3x12 + a) / 2y1
(f) x3 = λ2- x1 - x2, y3 = λ(x1 - x3) - y1
(g) P + Q = (x3, y3)
'''
def add_point(p1, p2):
if p1 == (0, 0):
return p2
if p2 == (0,0):
return p1
x1, y1 = p1
x2, y2 = p2
if x1 == x2 and y1 == -y2:
return (0, 0)
lamda = 0
if p1 == p2:
lamda = ((3*pow(x1,2,p)+a) * inverse(2*y1, p))
else:
lamda = ((y2-y1) * inverse(x2-x1, p))
x3 = (pow(lamda, 2) - x1 - x2) % p
y3 = (lamda*(x1 - x3) - y1) % p
return (x3, y3)
P = (493, 5564)
Q = (1539, 4742)
R = (4403,5202)
#S(x,y) = P + P + Q + R
s = add_point(P,add_point(P, add_point(Q, R)))
print(s)
#crypto{4215, 2162}Using the above curve, and the points P = (2339, 2213), find the point Q(x,y) = 7863 P by implementing the above algorithm.
Tiếp tục làm theo phương pháp đã được hướng dẫn nhưng lần này ra sẽ tái sử dụng lại hàm add_point(p1, p2) đã viết ở trên.
from Crypto.Util.number import *
a = 497
b = 1768
p = 9739
def add_point(p1, p2):
if p1 == (0, 0):
return p2
if p2 == (0,0):
return p1
x1, y1 = p1
x2, y2 = p2
if x1 == x2 and y1 == -y2:
return (0, 0)
lamda = 0
if p1 == p2:
lamda = ((3*pow(x1,2,p)+a) * inverse(2*y1, p))
else:
lamda = ((y2-y1) * inverse(x2-x1, p))
x3 = (pow(lamda, 2) - x1 - x2) % p
y3 = (lamda*(x1 - x3) - y1) % p
return (x3, y3)
'''
Input: P in E(Fp) and an integer n > 0
1. Set Q = P and R = O.
2. Loop while n > 0.
3. If n ≡ 1 mod 2, set R = R + Q.
4. Set Q = 2 Q and n = ⌊n/2⌋.
5. If n > 0, continue with loop at Step 2.
6. Return the point R, which equals nP.
'''
P = (2339, 2213)
n = 7863
#1. Set Q = P and R = O.
Q = P
R = (0, 0)
while n > 0:
#If n ≡ 1 mod 2, set R = R + Q.
if n % 2 == 1:
R = add_point(R, Q)
#Set Q = 2 Q and n = ⌊n/2⌋.
Q = add_point(Q, Q)
n = n//2
print(R)
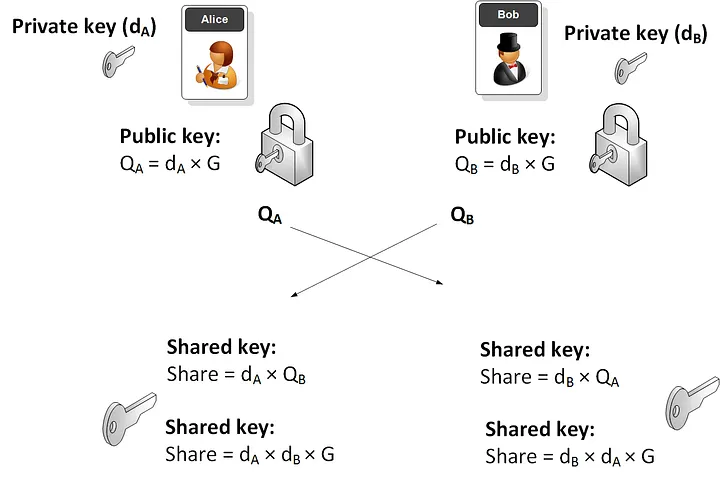
#crypto{9467, 2742}Using the curve, prime and generator:
E: Y^2 = X^3 + 497 X + 1768, p: 9739, G: (1804,5368)Calculate the shared secret after Alice sends you Q_A = (815, 3190), with your secret integer n_B = 1829
Generate a key by calculating the SHA1 hash of the x coordinate (take the decimal representation of the coordinate and cast it to a string). The flag is the hexdigest you find.
from Crypto.Util.number import *
import hashlib
#E: Y^2 = X^3 + 497 X + 1768, p: 9739, G: (1804,5368)
a = 497
b = 1768
p = 9739
G = (1804,5368)
def add_point(p1, p2):
if p1 == (0, 0):
return p2
if p2 == (0,0):
return p1
x1, y1 = p1
x2, y2 = p2
if x1 == x2 and y1 == -y2:
return (0, 0)
lamda = 0
if p1 == p2:
lamda = ((3*pow(x1,2,p)+a) * inverse(2*y1, p))
else:
lamda = ((y2-y1) * inverse(x2-x1, p))
x3 = (pow(lamda, 2) - x1 - x2) % p
y3 = (lamda*(x1 - x3) - y1) % p
return (x3, y3)
def Scalar_Mul(P, n):
Q = P
R = (0, 0)
while n > 0:
#If n ≡ 1 mod 2, set R = R + Q.
if n % 2 == 1:
R = add_point(R, Q)
#Set Q = 2 Q and n = ⌊n/2⌋.
Q = add_point(Q, Q)
n = n//2
return R
Q_A = (815, 3190)
n_B = 1829
#s = n_B * Q_A
s = Scalar_Mul(Q_A, n_B)
#Generate a key by calculating the SHA1 hash of the x coordinate
s = hashlib.sha1(str(s[0]).encode()).hexdigest()
print("crypto{" + s + "}")Using the curve, prime and generator:
E: Y^2 = X^3 + 497 X + 1768, p: 9739, G: (1804,5368)Calculate the shared secret after Alice sends you q_x = 4726, with your secret integer nB = 6534
Use the decrypt.py file to decode the flag
{'iv': 'cd9da9f1c60925922377ea952afc212c', 'encrypted_flag': 'febcbe3a3414a730b125931dccf912d2239f3e969c4334d95ed0ec86f6449ad8'}
Đầu tiên ta dựa vào phương trình của Ellip và q_x đã được cung cấp để tính y^2 và vì p = 3 mod 4 nên ta có thể tính y = (y^2)^[(p+1)//4] mod p
Bước tiếp theo alf tính shared_secret = Q*nB và lấy giá trị x truyền vào hàm decrypt() cùng với ciphertext và iv.
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
from Crypto.Util.number import *
import hashlib
a = 497
b = 1768
p = 9739
G = (1804,5368)
def add_point(p1, p2):
if p1 == (0, 0):
return p2
if p2 == (0,0):
return p1
x1, y1 = p1
x2, y2 = p2
if x1 == x2 and y1 == -y2:
return (0, 0)
lamda = 0
if p1 == p2:
lamda = ((3*pow(x1,2,p)+a) * inverse(2*y1, p))
else:
lamda = ((y2-y1) * inverse(x2-x1, p))
x3 = (pow(lamda, 2) - x1 - x2) % p
y3 = (lamda*(x1 - x3) - y1) % p
return (x3, y3)
def Scalar_Mul(P, n):
Q = P
R = (0, 0)
while n > 0:
#If n ≡ 1 mod 2, set R = R + Q.
if n % 2 == 1:
R = add_point(R, Q)
#Set Q = 2 Q and n = ⌊n/2⌋.
Q = add_point(Q, Q)
n = n//2
return R
def is_pkcs7_padded(message):
padding = message[-message[-1]:]
return all(padding[i] == len(padding) for i in range(0, len(padding)))
def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
# Derive AES key from shared secret
sha1 = hashlib.sha1()
sha1.update(str(shared_secret).encode('ascii'))
key = sha1.digest()[:16]
# Decrypt flag
ciphertext = bytes.fromhex(ciphertext)
iv = bytes.fromhex(iv)
cipher = AES.new(key, AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
if is_pkcs7_padded(plaintext):
return unpad(plaintext, 16).decode('ascii')
else:
return plaintext.decode('ascii')
#E: Y^2 = X^3 + 497 X + 1768, p: 9739, G: (1804,5368)
q_x = 4726
nB = 6534
y_2 = (pow(q_x,3) + 497*q_x + 1768) % p
q_y = pow(y_2, (p+1)//4, p)
Q = (q_x, q_y)
shared_secret = Scalar_Mul(Q, nB)[0]
iv = 'cd9da9f1c60925922377ea952afc212c'
ciphertext = 'febcbe3a3414a730b125931dccf912d2239f3e969c4334d95ed0ec86f6449ad8'
print(decrypt_flag(shared_secret, iv, ciphertext))
#crypto{3ff1c1ent_k3y_3xch4ng3}Spent my morning reading up on ECC and now I'm ready to start encrypting my messages. Sent a flag to Bob today, but you'll never read it.
Source:
from Crypto.Cipher import AES
from Crypto.Util.number import inverse
from Crypto.Util.Padding import pad, unpad
from collections import namedtuple
from random import randint
import hashlib
import os
# Create a simple Point class to represent the affine points.
Point = namedtuple("Point", "x y")
# The point at infinity (origin for the group law).
O = 'Origin'
FLAG = b'crypto{??????????????????????????????}'
def check_point(P: tuple):
if P == O:
return True
else:
return (P.y**2 - (P.x**3 + a*P.x + b)) % p == 0 and 0 <= P.x < p and 0 <= P.y < p
def point_inverse(P: tuple):
if P == O:
return P
return Point(P.x, -P.y % p)
def point_addition(P: tuple, Q: tuple):
# based of algo. in ICM
if P == O:
return Q
elif Q == O:
return P
elif Q == point_inverse(P):
return O
else:
if P == Q:
lam = (3*P.x**2 + a)*inverse(2*P.y, p)
lam %= p
else:
lam = (Q.y - P.y) * inverse((Q.x - P.x), p)
lam %= p
Rx = (lam**2 - P.x - Q.x) % p
Ry = (lam*(P.x - Rx) - P.y) % p
R = Point(Rx, Ry)
assert check_point(R)
return R
def double_and_add(P: tuple, n: int):
# based of algo. in ICM
Q = P
R = O
while n > 0:
if n % 2 == 1:
R = point_addition(R, Q)
Q = point_addition(Q, Q)
n = n // 2
assert check_point(R)
return R
def gen_shared_secret(Q: tuple, n: int):
# Bob's Public key, my secret int
S = double_and_add(Q, n)
return S.x
def encrypt_flag(shared_secret: int):
# Derive AES key from shared secret
sha1 = hashlib.sha1()
sha1.update(str(shared_secret).encode('ascii'))
key = sha1.digest()[:16]
# Encrypt flag
iv = os.urandom(16)
cipher = AES.new(key, AES.MODE_CBC, iv)
ciphertext = cipher.encrypt(pad(FLAG, 16))
# Prepare data to send
data = {}
data['iv'] = iv.hex()
data['encrypted_flag'] = ciphertext.hex()
return data
# Define the curve
p = 310717010502520989590157367261876774703
a = 2
b = 3
# Generator
g_x = 179210853392303317793440285562762725654
g_y = 105268671499942631758568591033409611165
G = Point(g_x, g_y)
# My secret int, different every time!!
n = randint(1, p)
# Send this to Bob!
public = double_and_add(G, n)
print(public)
# Bob's public key
b_x = 272640099140026426377756188075937988094
b_y = 51062462309521034358726608268084433317
B = Point(b_x, b_y)
# Calculate Shared Secret
shared_secret = gen_shared_secret(B, n)
# Send this to Bob!
ciphertext = encrypt_flag(shared_secret)
print(ciphertext)output:
Point(x=280810182131414898730378982766101210916, y=291506490768054478159835604632710368904)
{'iv': '07e2628b590095a5e332d397b8a59aa7', 'encrypted_flag': '8220b7c47b36777a737f5ef9caa2814cf20c1c1ef496ec21a9b4833da24a008d0870d3ac3a6ad80065c138a2ed6136af'}
Tổng quan tại challenge này xoay quanh bài toán: (G*n = P) với G và P là 2 điểm trên đường cong Ellip đã cho và ta cần tim được ndựa trên những dữ kiện đã thu được trong source code.
Để tìm được n ta sẽ sử dụng thuật toán Pohlig-Hellman để xử lý:
http://koclab.cs.ucsb.edu/teaching/ecc/project/2015Projects/Sommerseth+Hoeiland.pdf
Điều kiện để sử dụng được thuật toán Pohlig-Hellman là đường cong Ellip được khai thác phải là đường cong Ellip yếu, cụ thể trong challenge này là việc E.order() là một smooth number.
sage: p = 310717010502520989590157367261876774703
sage: p = 310717010502520989590157367261876774703
....: a = 2
....: b = 3
....:
....: E = EllipticCurve(GF(p), [a, b])
sage: E.order()
310717010502520989590206149059164677804
sage: factor(E.order())
2^2 * 3^7 * 139 * 165229 * 31850531 * 270778799 * 179317983307Chi tiết:
https://l0z1k.com/pohlig_hellman_attack
from Crypto.Cipher import AES
from sage.all import *
p = 310717010502520989590157367261876774703
a = 2
b = 3
E = EllipticCurve(GF(p), [a, b])
g_x = 179210853392303317793440285562762725654
g_y = 105268671499942631758568591033409611165
G = E.point((g_x, g_y))
P = E.point((280810182131414898730378982766101210916, 291506490768054478159835604632710368904))
primes = []
for i in factor(P.order()):
primes.append(i[0]**i[1])
dlogs = []
for i in primes:
t = int(G.order() / i)
dlog = discrete_log(t*P, t*G, operation = '+')
dlogs.append(dlog)
n = CRT_list(dlogs, primes)
print(n)
#47836431801801373761601790722388100620Sau khi có n ta sẽ giải như bình thường.
from Crypto.Cipher import AES
from Crypto.Util.number import inverse
from Crypto.Util.Padding import pad, unpad
from collections import namedtuple
import hashlib
import os
# Create a simple Point class to represent the affine points.
Point = namedtuple("Point", "x y")
# The point at infinity (origin for the group law).
O = 'Origin'
def check_point(P: tuple):
if P == O:
return True
else:
return (P.y**2 - (P.x**3 + a*P.x + b)) % p == 0 and 0 <= P.x < p and 0 <= P.y < p
def point_inverse(P: tuple):
if P == O:
return P
return Point(P.x, -P.y % p)
def point_addition(P: tuple, Q: tuple):
# based of algo. in ICM
if P == O:
return Q
elif Q == O:
return P
elif Q == point_inverse(P):
return O
else:
if P == Q:
lam = (3*P.x**2 + a)*inverse(2*P.y, p)
lam %= p
else:
lam = (Q.y - P.y) * inverse((Q.x - P.x), p)
lam %= p
Rx = (lam**2 - P.x - Q.x) % p
Ry = (lam*(P.x - Rx) - P.y) % p
R = Point(Rx, Ry)
assert check_point(R)
return R
def double_and_add(P: tuple, n: int):
# based of algo. in ICM
Q = P
R = O
while n > 0:
if n % 2 == 1:
R = point_addition(R, Q)
Q = point_addition(Q, Q)
n = n // 2
assert check_point(R)
return R
def gen_shared_secret(Q: tuple, n: int):
# Bob's Public key, my secret int
S = double_and_add(Q, n)
return S.x
def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
# Derive AES key from shared secret
sha1 = hashlib.sha1()
sha1.update(str(shared_secret).encode('ascii'))
key = sha1.digest()[:16]
# Decrypt flag
ciphertext = bytes.fromhex(ciphertext)
iv = bytes.fromhex(iv)
cipher = AES.new(key, AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
if is_pkcs7_padded(plaintext):
return unpad(plaintext, 16).decode('ascii')
else:
return plaintext.decode('ascii')
# Define the curve
#E: Y^2 = X^3 + 2X + 3
p = 310717010502520989590157367261876774703
a = 2
b = 3
# Generator
g_x = 179210853392303317793440285562762725654
g_y = 105268671499942631758568591033409611165
G = Point(g_x, g_y)
# My secret int, different every time!!
n = 47836431801801373761601790722388100620
# Send this to Bob!
# public = n*g
public = double_and_add(G, n)
# Bob's public key
b_x = 272640099140026426377756188075937988094
b_y = 51062462309521034358726608268084433317
B = Point(b_x, b_y)
# Calculate Shared Secret
shared_secret = gen_shared_secret(B, n)
iv = '07e2628b590095a5e332d397b8a59aa7'
enc_flag = '8220b7c47b36777a737f5ef9caa2814cf20c1c1ef496ec21a9b4833da24a008d0870d3ac3a6ad80065c138a2ed6136af'
flag = decrypt_flag(shared_secret, iv, enc_flag)
print(flag)
#crypto{n07_4ll_curv3s_4r3_s4f3_curv3s}from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
from random import randint
import hashlib
from sage.all import *
FLAG = b'crypto{??????????????????????}'
def gen_public_key():
private = randint(1, E.order() - 1)
public = G * private
return(public, private)
def shared_secret(public_key, private_key):
S = public_key * private_key
return S.xy()[0]
def encrypt_flag(flag):
# Bob's public key
b_x = 0x7f0489e4efe6905f039476db54f9b6eac654c780342169155344abc5ac90167adc6b8dabacec643cbe420abffe9760cbc3e8a2b508d24779461c19b20e242a38
b_y = 0xdd04134e747354e5b9618d8cb3f60e03a74a709d4956641b234daa8a65d43df34e18d00a59c070801178d198e8905ef670118c15b0906d3a00a662d3a2736bf
B = E(b_x, b_y)
# Calculate shared secret
A, nA = gen_public_key()
print(f'Public Key: {A}')
secret = shared_secret(B, nA)
# Derive AES key from shared secret
sha1 = hashlib.sha1()
sha1.update(str(secret).encode('ascii'))
key = sha1.digest()[:16]
# Encrypt flag
iv = os.urandom(16)
cipher = AES.new(key, AES.MODE_CBC, iv)
ciphertext = cipher.encrypt(pad(FLAG, 16))
# Prepare encryption to send
data = {}
data['iv'] = iv.hex()
data['encrypted_flag'] = ciphertext.hex()
return data
# Curve params
p = 0xa15c4fb663a578d8b2496d3151a946119ee42695e18e13e90600192b1d0abdbb6f787f90c8d102ff88e284dd4526f5f6b6c980bf88f1d0490714b67e8a2a2b77
a = 0x5e009506fcc7eff573bc960d88638fe25e76a9b6c7caeea072a27dcd1fa46abb15b7b6210cf90caba982893ee2779669bac06e267013486b22ff3e24abae2d42
b = 0x2ce7d1ca4493b0977f088f6d30d9241f8048fdea112cc385b793bce953998caae680864a7d3aa437ea3ffd1441ca3fb352b0b710bb3f053e980e503be9a7fece
# Define curve
E = EllipticCurve(GF(p), [a, b])
# Protect against Pohlig-Hellman Algorithm
assert is_prime(E.order())
# Create generator
G = E.gens()[0]
print(f'Generator: {G}')
encrypted_flag = encrypt_flag(FLAG)
print(encrypted_flag)Out put:
Generator: (3034712809375537908102988750113382444008758539448972750581525810900634243392172703684905257490982543775233630011707375189041302436945106395617312498769005 : 4986645098582616415690074082237817624424333339074969364527548107042876175480894132576399611027847402879885574130125050842710052291870268101817275410204850 : 1)
Public Key: (4748198372895404866752111766626421927481971519483471383813044005699388317650395315193922226704604937454742608233124831870493636003725200307683939875286865 : 2421873309002279841021791369884483308051497215798017509805302041102468310636822060707350789776065212606890489706597369526562336256272258544226688832663757 : 1)
{'iv': '719700b2470525781cc844db1febd994', 'encrypted_flag': '335470f413c225b705db2e930b9d460d3947b3836059fb890b044e46cbb343f0'}Tại challenge này ta sẽ phải sử dụng một hình thức tấn công khác có tên là Smart's attack.
https://crypto.stackexchange.com/questions/70454/why-smarts-attack-doesnt-work-on-this-ecdlp
(Dùng luôn script ở phần cmt)
https://wstein.org/edu/2010/414/projects/novotney.pdf
Cuộc tấn công của Smart (Smart's attack) là một phương pháp tấn công logarit rời rạc trên đường cong elliptic (ECC). Được giới thiệu bởi nhà toán học Robert Smart năm 1987, cuộc tấn công này tận dụng sự khác biệt trong độ dài các phần tử của các nhóm con của đường cong elliptic.
Giả sử rằng attacker biết giá trị của d = log_g(h) trong nhóm con có bậc h, với g là điểm cơ sở của đường cong elliptic. Với d, attacker có thể tìm được khóa bí mật của họ. Vì vậy, vấn đề đặt ra là làm thế nào để tìm giá trị d.
Smart's attack đề xuất tìm các điểm P, Q thuộc vào cùng một nhóm con của đường cong elliptic. Từ P và Q, attacker có thể tìm được một điểm R = P + Q. Sử dụng tính chất đối xứng của phép cộng trên đường cong elliptic, attacker cũng có thể tìm được một điểm S sao cho R + S = 2P.
Dựa trên giá trị của R và S, attacker có thể tính toán bậc của P và Q trong cùng một nhóm con. Sau đó, attacker có thể sử dụng giải thuật Baby-step Giant-step để tìm giá trị của d.
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import hashlib
from sage.all import *
def is_pkcs7_padded(message):
padding = message[-message[-1]:]
return all(padding[i] == len(padding) for i in range(0, len(padding)))
def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
# Derive AES key from shared secret
sha1 = hashlib.sha1()
sha1.update(str(shared_secret).encode('ascii'))
key = sha1.digest()[:16]
# Decrypt flag
ciphertext = bytes.fromhex(ciphertext)
iv = bytes.fromhex(iv)
cipher = AES.new(key, AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
if is_pkcs7_padded(plaintext):
return unpad(plaintext, 16).decode('ascii')
else:
return plaintext.decode('ascii')
def SmartAttack(P,Q,p):
E = P.curve()
Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])
P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
for P_Qp in P_Qps:
if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
break
Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
for Q_Qp in Q_Qps:
if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
break
p_times_P = p*P_Qp
p_times_Q = p*Q_Qp
x_P,y_P = p_times_P.xy()
x_Q,y_Q = p_times_Q.xy()
phi_P = -(x_P/y_P)
phi_Q = -(x_Q/y_Q)
k = phi_Q/phi_P
return ZZ(k)
p = 0xa15c4fb663a578d8b2496d3151a946119ee42695e18e13e90600192b1d0abdbb6f787f90c8d102ff88e284dd4526f5f6b6c980bf88f1d0490714b67e8a2a2b77
a = 0x5E009506FCC7EFF573BC960D88638FE25E76A9B6C7CAEEA072A27DCD1FA46ABB15B7B6210CF90CABA982893EE2779669BAC06E267013486B22FF3E24ABAE2D42
b = 0x2CE7D1CA4493B0977F088F6D30D9241F8048FDEA112CC385B793BCE953998CAAE680864A7D3AA437EA3FFD1441CA3FB352B0B710BB3F053E980E503BE9A7FECE
E = EllipticCurve(GF(p), [a, b])
Q_A = E(4748198372895404866752111766626421927481971519483471383813044005699388317650395315193922226704604937454742608233124831870493636003725200307683939875286865, 2421873309002279841021791369884483308051497215798017509805302041102468310636822060707350789776065212606890489706597369526562336256272258544226688832663757)
Q_B = E(0x7f0489e4efe6905f039476db54f9b6eac654c780342169155344abc5ac90167adc6b8dabacec643cbe420abffe9760cbc3e8a2b508d24779461c19b20e242a38, 0xdd04134e747354e5b9618d8cb3f60e03a74a709d4956641b234daa8a65d43df34e18d00a59c070801178d198e8905ef670118c15b0906d3a00a662d3a2736bf)
G = E(3034712809375537908102988750113382444008758539448972750581525810900634243392172703684905257490982543775233630011707375189041302436945106395617312498769005, 4986645098582616415690074082237817624424333339074969364527548107042876175480894132576399611027847402879885574130125050842710052291870268101817275410204850)
nA = SmartAttack(G, Q_A, p)
shared_secret = (Q_B * nA).xy()[0]
iv = "719700b2470525781cc844db1febd994"
ciphertext = "335470f413c225b705db2e930b9d460d3947b3836059fb890b044e46cbb343f0"
print(decrypt_flag(shared_secret, iv, ciphertext))
#crypto{H3ns3l_lift3d_my_fl4g!}from Crypto.Util.number import getPrime
from Crypto.Random import random
from Crypto.Cipher import AES
from Crypto.Util.number import inverse
from Crypto.Util.Padding import pad, unpad
import hashlib
FLAG = b"crypto{???????????????????}"
def gen_key_pair(G, nbits):
n = random.getrandbits(nbits)
P = n*G
return P.xy()[0], n
def gen_shared_secret(P, n):
S = n*P
return S.xy()[0]
def encrypt_flag(shared_secret: int):
# Derive AES key from shared secret
sha1 = hashlib.sha1()
sha1.update(str(shared_secret).encode('ascii'))
key = sha1.digest()[:16]
# Encrypt flag
iv = os.urandom(16)
cipher = AES.new(key, AES.MODE_CBC, iv)
ciphertext = cipher.encrypt(pad(FLAG, 16))
# Prepare data to send
data = {}
data['iv'] = iv.hex()
data['encrypted_flag'] = ciphertext.hex()
return data
# Efficient key exchange
nbits = 64
pbits = 256
# Curve parameters
p = getPrime(pbits)
a = 1
b = 4
E = EllipticCurve(GF(p), [a,b])
G = E.gens()[0]
print(f"Sending curve parameters:")
print(f"{E}")
print(f"Generator point: {G}\n")
# Generate key pairs
ax, n_a = gen_key_pair(G, nbits)
bx, n_b = gen_key_pair(G, nbits)
print(f"Alice sends public key: {ax}")
print(f"Bob sends public key: {bx}\n")
# Calculate point from Bob
B = E.lift_x(bx)
# Encrypted flag with shared secret
shared_secret = gen_shared_secret(B,n_a)
encrypted_flag = encrypt_flag(shared_secret)
print(f"Alice sends encrypted_flag: {encrypted_flag}")Out put:
Sending curve parameters:
Elliptic Curve defined by y^2 = x^3 + x + 4 over Finite Field of size 99061670249353652702595159229088680425828208953931838069069584252923270946291
Generator point: (43190960452218023575787899214023014938926631792651638044680168600989609069200 : 20971936269255296908588589778128791635639992476076894152303569022736123671173 : 1)
Alice sends public key: 87360200456784002948566700858113190957688355783112995047798140117594305287669
Bob sends public key: 6082896373499126624029343293750138460137531774473450341235217699497602895121
Alice sends encrypted_flag: {'iv': 'ceb34a8c174d77136455971f08641cc5', 'encrypted_flag': 'b503bf04df71cfbd3f464aec2083e9b79c825803a4d4a43697889ad29eb75453'}Tìm y từ x đã cho và dùng Pohlig_Hellman attack như 1 challenge ở trên.
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import hashlib
from sage.all import *
def is_pkcs7_padded(message):
padding = message[-message[-1]:]
return all(padding[i] == len(padding) for i in range(0, len(padding)))
def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
# Derive AES key from shared secret
sha1 = hashlib.sha1()
sha1.update(str(shared_secret).encode('ascii'))
key = sha1.digest()[:16]
# Decrypt flag
ciphertext = bytes.fromhex(ciphertext)
iv = bytes.fromhex(iv)
cipher = AES.new(key, AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
if is_pkcs7_padded(plaintext):
return unpad(plaintext, 16).decode('ascii')
else:
return plaintext.decode('ascii')
p = 99061670249353652702595159229088680425828208953931838069069584252923270946291
a = 1
b = 4
E = EllipticCurve(GF(p), [a,b])
G = E(43190960452218023575787899214023014938926631792651638044680168600989609069200, 20971936269255296908588589778128791635639992476076894152303569022736123671173)
P_A = E.lift_x(ZZ(87360200456784002948566700858113190957688355783112995047798140117594305287669))
P_B = E.lift_x(ZZ(6082896373499126624029343293750138460137531774473450341235217699497602895121))
primes = [p for p, _ in E.order().factor()][:-2]
dlogs = []
for fac in primes:
t = int(G.order()) // int(fac)
dlog = (t*G).discrete_log(t*P_A)
dlogs += [dlog]
nA = crt(dlogs, primes)
shared_secret = (nA*P_B).xy()[0]
iv = "ceb34a8c174d77136455971f08641cc5"
ciphertext = "b503bf04df71cfbd3f464aec2083e9b79c825803a4d4a43697889ad29eb75453"
print(decrypt_flag(shared_secret, iv, ciphertext))
#crypto{d0nt_l3t_n_b3_t00_sm4ll}