README.md

Numerical Recipes

A simple numerical analysis tool which can perform differentiation, integration and root approximation for functions using a multitude of methods. For description of each of these methods, refer to Numerical Analysis.

Computational Capabilites

• Numerical Differentiation
• Numerical Integration
  • Riemann Sum
    • Left Riemann Sum
    • Right Riemann Sum
    • Midpoint Rule
    • Trapezoidal Rule
  • Simpsons' Rule
• Root Approximation
  • Newton-Raphson Method
  • Bisection Method
  • Secant Method

Key Features

• User-defined Precision: The program gives the freedom of choosing the degree of precision upto which the result is required. This is specified by the parameter eps which stands for $\epsilon$.

• Maximum Iterations: User can define the maximum number of iterations of the program. Program terminates for whichever of the two conditions is met first, whether the required precision is reached, or the maximum iterations have elapsed.

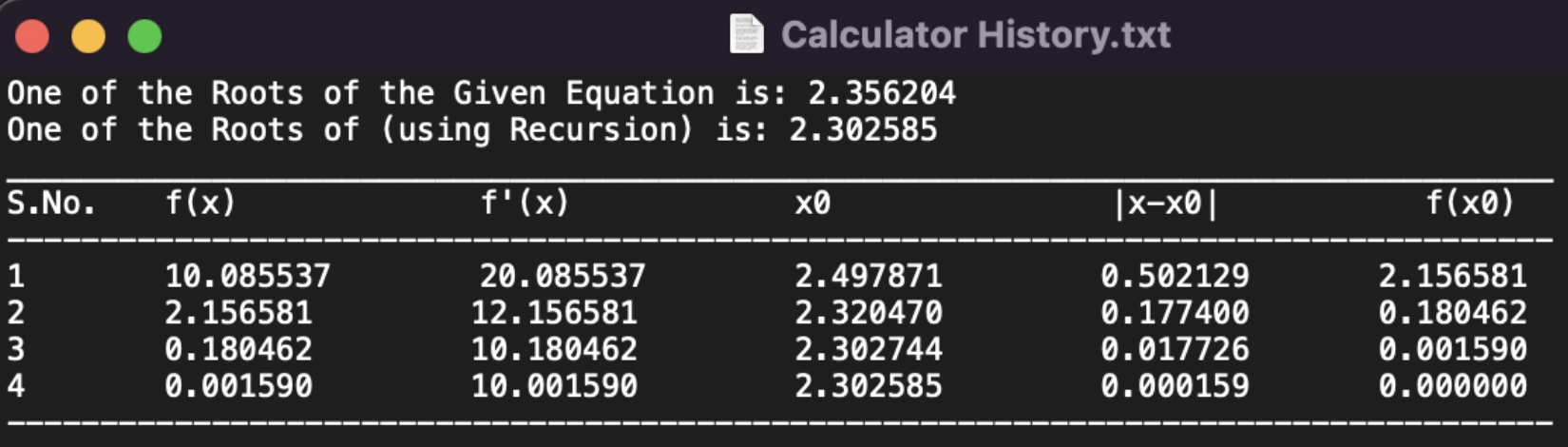
• Calculator History: The most useful of this application is perhaps that it stores the result for each iteration in a .txt file so that the user can analyse how the function behaves after each iteration, this also gives away the trend of how the result is reached. For example, the function call fprintNewtonRaphson(f,eps,x,maxIterations) for $f(x)=e^{x}-10$ results in the following .txt file.

  

Limitations

• Function Input: It is challenging to take function input from the CLI. One of the solutions could be to map certain strings to functions in the <math.h> library in C using macros, but that is rather tedious and non-elegant.
• Derivative Error Term: The function derivative(f,x0) is called numerous times from within multiple functions. This function itself is not error free, therefore it adds to the number of iterations required for reaching the desired level of precision in the result.

Future Scope

• LaTeX Compilation: Additional functionality of typesetting the result and storing it in a .pdf format could be introduced. For example if user computes the approximation of the Gaussian Integral using the bounds from -5 to +5, which results in only an error of around $10^{-12}$, we could depict this as under in a .pdf output file.

$$\int_{-5}^{+5}e^{-x^{2}}dx\approx 1.77245$$

• Additional Methods: More advanced computational techniques could be incorporated into the program to improve the computation time and increase the degree of precision reached at lower number of iterations. For instance, Regula-Falsi, Ridders' Method for Root Finding, Monte Carlo Method for Numerical Integration etc.

• Game Base: The logic laid out in this program could be used to construct a gamified educational tool that generates a mathematical expression on screen and takes in user input. If user inputs a value within a preset error bound of the actual value of the expression, which could be basis for the difficulty level of the game, the input gets classified as good and the user is awarded points correspondingly.