Resumo criado pelo aluno João Pedro Trevisan
O Professor Zorzo usa a nomenclatura dos autômatos em inglês. Isso significa que as siglas usadas em aula podem diferir das siglas usadas no vídeo.
Este resumo é feito para concordar com as aulas, uma vez que seus exercícios e provas terão a nomenclatura usada nelas. Ainda assim, aqui tem uma lista de significados e equivalências:
- DFA = Autômato Finito Determinístico, Definite Finite Automata
- NFA = Autômato Finito Não Determinístico, Non-deterministic Finite Automata
- εNFA = Aut. Fin. Não Det. com Transições Vazias
Quando tratamos de linguagens regulares, existem 3 formalismos de estudo com utilidades diferentes:
- Autômato Finito:
- Formalismo operacional (reconhecedor de sentenças)
- Expressão Regular:
- Formalismo denotacional (gerador de sentenças)
- Gramática regular:
- Formalismo axiomático (formador de sentenças)
Sistemas de estados finitos são os mais simples modelos computacionais e a forma com a qual os enxergaremos é a de modelos matemáticos que descrevem um sistema com entrada e saída.
Sistemas de estados finitos tem uma quantidade pré-definida de estados que mostram a situação atual e passada do sistema. Além disso existe um conjunto de transições que expressa os movimentos possíveis de um estado para outro e um dispositivo hipotético chamado de controle que lê as entradas externas e move o sistema de um estado para outro.
Os Autômatos Finitos Determinísticos (conhecidos como DFAs) possuem uma definição formal denotada como "DFA M" ou "AF-d M" na forma:
M=(Q, Ʃ, δ, q0, F), onde Q = Conjunto finito de estados Ʃ = Conjunto finito de símbolos de entrada δ = Função de transição q0 = Estado inicial ∈Q F = um conjunto de estados finais, ou de aceitação (F ⊆ Q)
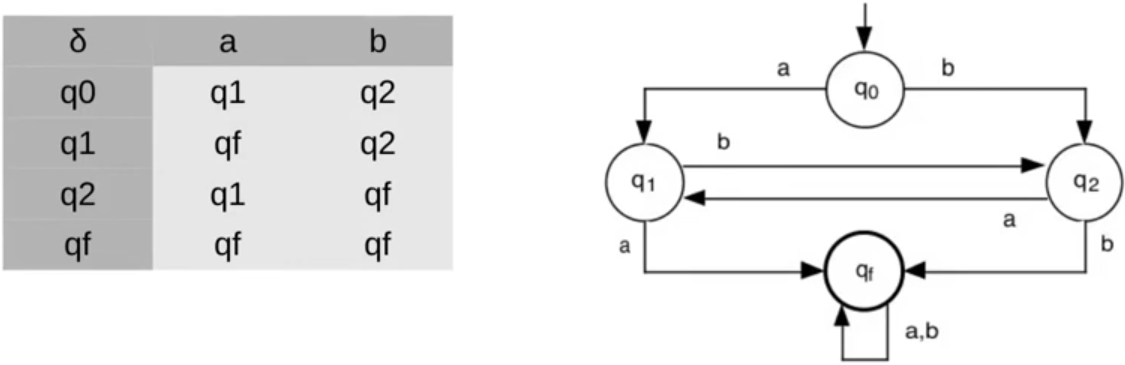
Tomemos como exemplo o autômato M1 que reconhece a linguagem L = {w | w possui aa ou bb como subpalavra}
M1 = ({a, b}, {q0, q1, q2, qf}, δ, q0, {qf})
δ é dado pela tabela.
Vale a pena estudar o slide do Zorzo pra ver mais exemplos.
Quando um autômato recebe uma cadeia de entrada ele a processa e produz uma saída binária que aceita ou rejeita a cadeia. A cadeia em questão é processada da esquerda para a direita começando do estado inicial do autômato, após ler um símbolo move-se de acordo com a função de transição daquele estado. A saída do autômato vem depois de completa a leitura da cadeia.
Quanto ao projeto de autômatos finitos determinísticos, não há regras. Eles geralmente são criados através de tentativa e erro e por isso podem acabar não sendo autômatos mínimos (coisa que abordaremos adiante).
Existem portanto diferentes autômatos que serão capazes de reconhecer as mesmas linguagens e nestes casos eles serão equivalentes. L(M1) = L(M2). A linguagem L só é dita regular se existe um autômato finito M tal que L = L(M).
Um outro tipo de autômato é o NFA, o Autômato Finito Não Determinístico. Seu não determinismo implica que a partir de um determinado estado e símbolo lido ele pode assumir mais que um estado diferente.
Este não determinismo não aumenta o poder computacional do autômato, mas torna mais fácil a criação de soluções para nós humanos. Todos os DFA podem ser convertidos em NFA.
O não determinismo do autômato sob estudo ficará evidente no diagrama quando houverem mais que uma ou nenhuma seta apontando para um estado. Já na tabela, observaremos uma tabela cujas células podem conter zero ou mais estados, diferente da tabela de um DFA que é uniformemente preenchida.
Assim como um DFA, os NFA tem a forma M=(Q, Ʃ, δ, q0, F).
É possível converter todo NFA em um DFA e na maioria dos casos eles terão o mesmo número de estados, porém mais transições. A conversão consiste em pegar todas combinações de estados e agregar as transições do NFA, cada combinação de estados do NFA é um estado do DFA. Nos slides 64 ~ 78 há um exemplo simples.
Há também um segundo tipo de autômato finito não determinístico que é o Autômato Finito com Movimentos Vazios. O movimento vazio contido neste formalismo é a generalização de movimentos não determinísticos, ele consiste de uma transição sem leitura de símbolo. Vale lembrar que isso também não aumenta o poder computacional do autômato e que os εNFA podem ser convertidos em NFAs que podem se tornar DFAs.
Bem como seus antecessores, o εNFA tem a forma M=(Q, Ʃ, δ, q0, F).
No diagrama, quando puder ser realizado um movimento vazio de um estado para outro basta indicar com uma seta com o símbolo lambda ou epsolon. Na tabela deverá haver uma coluna para os movimentos vazios também.
Autômatos finitos não determinísticos e autômatos finitos determinísticos. Por teorema, a classe dos autômatos finitos determinísticos é equivalente a classe dos autômatos finitos não determinísticos.
Essa conversão pode ser feita algoritmicamente, seguem os passos:
- Construir a tabela do NFA que queremos converter.
- Construir a nova tabela do DFA que queremos criar:
- Seus estados serão as combinações de estados possíveis do NFA
- O total de estados será 2^n
- Para um estado que é um conjunto, o novo estado será a união das transições
- Marcar os novos estados finais
- Todos estados que contiverem um estado final em seu conjunto
- Eliminar estados...
- ...Inalcançáveis
- ...Não finais que não possuem saída
- Verificar se há no grafo algum ciclo inalcançável
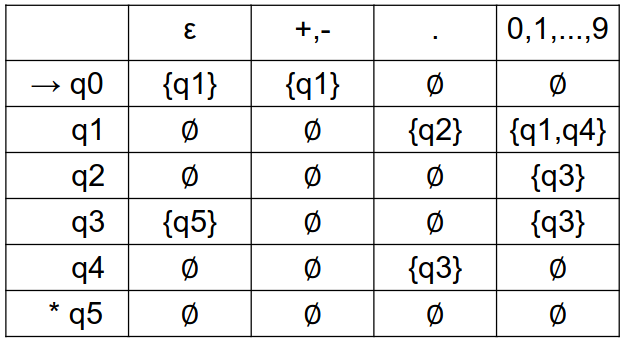
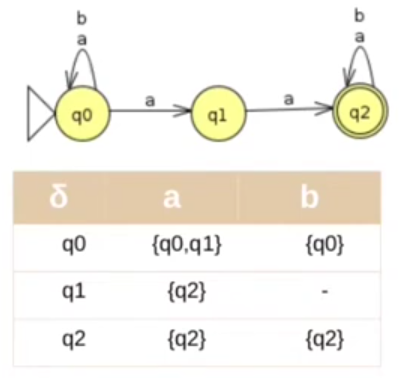
Passo 1: Tomamos o autômato e geramos sua tabela.
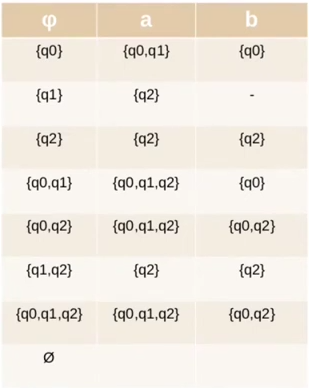
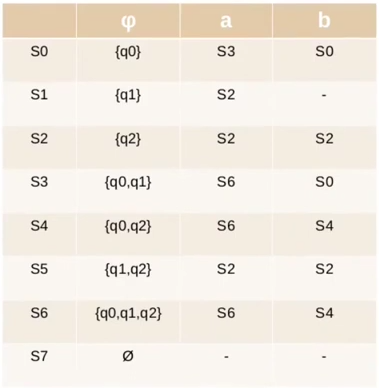
Passo 2: Criamos a tabela do DFA que estamos buscando. No nosso caso ela terá 2³ estados.
Para ver a tabela sendo feita passo a passo veja o vídeo LFA11. Para facilitar a construção do grafo do nosso autômato, faz bem nomear cada estado na nossa tabela, veja:
Passo 3: Nossos estados finais são aqueles que possuem em seu conjunto o estado q2. Isto é:
- S2
- S4
- S5
- S6
Passo 4: Os estados inalcançáveis são mais facilmente eliminados se seguirmos uma ordem:
- Quais estados não são alcançados por ninguém?
- S1, S5 e S7
- Retirados estes estados, mais algum estado não é mais alcançado?
- S2 não é mais alcançado pro outros estados
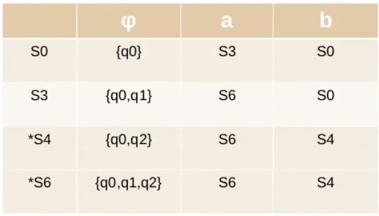
Feito isso, nossa tabela estará assim:
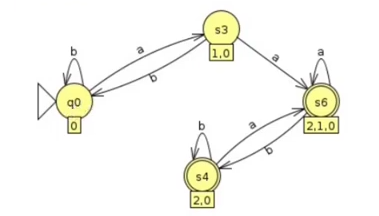
Passo 5: Desenhamos o grafo e vemos que ele não possui loops inalcançáveis
Autômatos Finitos Não Determinísticos e Autômtos finitos com movimentos vazios. Esses dois autômatos são equivalentes por teorema.
Para transformar um εNFA não há um algoritmo, mas quando houver um movimento vazio analisaremos ambos o estado de origem quanto o estado destino e substituímos lambda por todos os símbolos de um dado alfabeto. Depois disso analisaremos caso a caso.
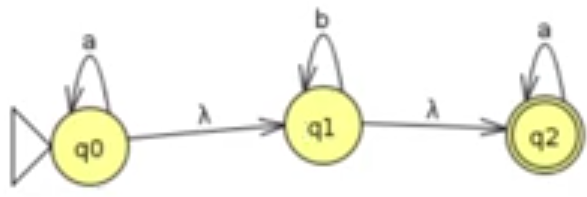
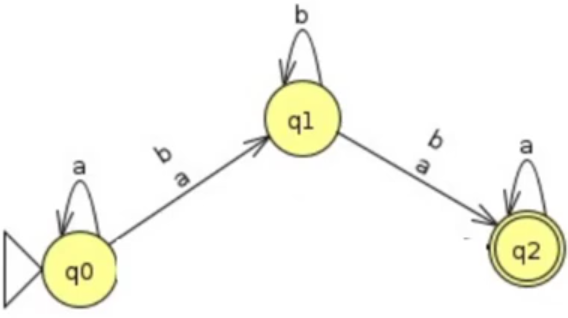
Note o exemplo a seguir:
Nosso primeiro passo é substituir lambda por todos os símbolos do alfabeto:
Agora, tendo como parâmetro o autômato original devemos avaliar se os mesmos movimentos são possíveis. Vejamos:
No original deve ser possível chegar a qualquer estado sem nenhum custo, portanto nos perguntamos "estando em q0, eu devo consumir algo além de a para chegar a q1?", a resposta é não, então mantemos o a naquela transição.
Estando em q1, eu consigo chegar a q2 consumindo apenas um b que era exigido no original? Sim, portanto está correto o b naquela transição.
Ainda que no q0 original eu não saiba consumir b eu poderia ir para q1 pela transição vazia e consumir lá, então não há problemas em banter b na primeira transição. O mesmo vale entre q1 e q2 para mantermos a na segunda transição.
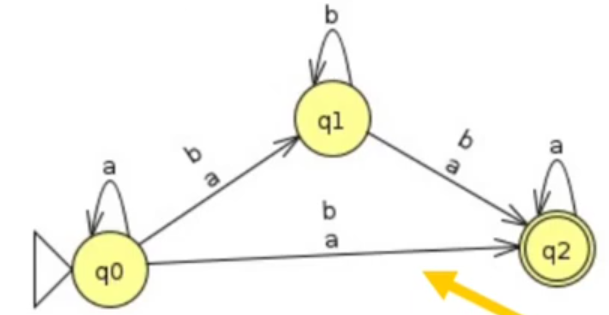
Temos um problema pois no original deveria ser possível estar em q0, receber um b e chegar à q2. Da mesma forma, deveríamos ser capazes de chegar de q0 a q2 recebendo apenas um símbolo a. Portanto devemos adicionar mais uma transição:
Perceba que ainda falta algo. Deveria ser possível receber 2 transições vazias e chegar a um estado final, ou seja, finalizar sem consumir nada. Para resolver isso q0 deve ser um estado de aceitação, mas eu não vou colocar uma imagem nova.
As outras equivalências (εNFA -> NFA e DFA -> NFA) não serão exemplificadas aqui, existem exemplos nos slides do professor Zorzo.
Se você tiver alguma dúvida, sugestão ou precisar de suporte, por favor, sinta-se à vontade para entrar em contato conosco:
- E-mail: [email protected]
Você também pode criar uma Issue no GitHub para relatar problemas, sugerir melhorias ou contribuir para o desenvolvimento do PET-COLAB. Estamos sempre abertos para receber feedback e colaboração. Obrigado!