Resumo criado pelo aluno João Pedro Trevisan
De inicio tomaremos a tarefa de criar um autômato para gerar a linguagem {0^n 1^n|n>=0}. Uma ideia inicial poderia ser criar um loop para gerar 0 e um outro para gerar 1, contudo isso é um problema pois depois de se gerar os 0s não há memória que indique quantos 1s gerar.
Parece ser muito difícil gerar um autômato finito para esta linguagem, até porque isso é impossível. Agora surge uma questão: como aferir a possibilidade de se criar um autômato para uma linguagem sem realizar uma busca exaustiva por este autômato?
É aqui que entra o Lema do Bombeamento.
Chamamos a classe de linguagens aceitas por um DFA de linguagens regulares e o lema do bombeamento é uma das propriedades das linguagens regulares.
Como base do lema do bombeamento temos o princípio da casa dos pombos. Ele nos diz que dado um autômato com n estados diferentes, se for gerada uma palavra com mais que n termos temos o indicativo de que se repetiram estados do autômato na geração dessa palavra. Este vídeo explica bem esta questão.
Outro princípio que nos leva ao lema é que em linguagens regulares, palavras de n ou mais termos geradas por autômatos com n estados sempre existirá uma estrutura que se repete. O estado que se repete pode ocorrer no inicio do processamento.
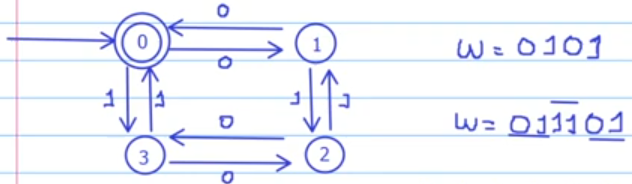
Tomemos o exemplo a seguir:
Note que das palavras geradas, a primeira tem o número de termos igual a o número de estados, além de visitar cada um deles antes de terminar na repetição do primeiro, que é inicial e final.
Já na segunda palavra, perceba que quando ela alcança o estado 2 é possível que o autômato fique em um loop gerando infinitos 1s. A palavra poderia ter a porção "11" repetida ad infinitum para depois buscar um estado final.
O lema do bombeamento para linguagens regulares enuncia: Seja L uma linguagem regular. Então existe uma constante k para toda string w em L tal que |w| >= k, podemos dividir w em três strings, w=xyz de forma que:
- y != ε
- |xy| <= k
- Para todo k>=0, a string x(y^k)z também estará em L
No nosso caso da palavra w=011101 teremos:
- w = 011101 -> x = 01
- w = 011101 -> y = 11
- w = 011101 -> z = 01
Perceba que tendo a fração 11 como y (nosso loop) podemos ter uma repetição infinita desse termo (y^k). Pode-se bombear a porção y da palavra gerada por um autômato finito determinístico reconhecedor de uma linguagem regular.
O lema do bombeamento serve então para mostra que uma linguagem não é regular, pois ao supormos que ela seja regular e tentarmos aplicar nela o bombeamento é possível se chegar a um absurdo que desprova sua regularidade.
Tomemos como exemplo a linguagem exemplificada no inicio deste resumo: L = {0^n 1^n|n>=0}
Pelo lema do bombeamento existe a constante k, então tomaremos uma palara w=0^k1^k pertencente a L. Para dividir w em xyz com |xy| <= k e |y| > 0 temos que ter:
- y = 0^i com i > 0
- xz = 0^k-m-i 0^m 1^k
Note que neste exemplo temos como primeira parte da palavra 0^k. Isso significa dizer que a substring xy é formada apenas por 0s pois |xy| <= k. Posta esta afirmação, sabemos que na substring y deve haver pelo menos um símbolo 0 pois ele não pode ser vazio. Denotaremos como y = 0^i, i>0
Já a substring x pode ser vazia, então denotaremos x = 0^j, j>=0.
A substring z por sua vez pode conter símbolos 0, mas isso não é uma garantia. Contudo, ele deve conter todos os k símbolos 1, fazendo com que tenhamos z = 0^m1^k, m>=0.
Destas expressões deriva-se que xz = 0^k-m-i 0^m 1^k = 0^k-i 1^k com y^0
Perceba que com xy⁰z = 0^k-i 1^k a temos a aceitação de uma palavra que tem número de 0s diferente do número de 1s, ou seja, um absurdo que mostra que esta linguagem não é regular.
Vale a pena assistir o vídeo UFC11.2 pois ele entra em detalhes em uma série de exemplos, neste resumo paramos de falar de bombeamento por aqui.
Sejam A e B linguagens, operações regulares são:
- União: A ⋃ B = {w|w∈A ou w∈B}
- Concatenação: AB = {wx|w∈A e x∈B}
- Estrela: A* = {w1, w2, w3... wk|k>0 e wi∈A}
- Entenda-se como qualquer concatenação dos símbolos dessa linguagem, inclusive ε.
- Interseção: A ⋂ B = {w|w∈A e w∈B}
- Complemento: A^c = Todas cadeias do alfabeto exceto as que estão em A
- Diferença: A\B ou A - B = {w|w∈A e w∉B}
- Reverso: A^R = {w^R|w∈A} (inverte todas as cadeias)
Trabalharemos principalmente com união, concatenação e estrela, para elas valem as seguintes propriedades:
- A ⋃ B = B ⋃ A (comutativa)
- A ⋃ (B ⋃ C) = (A ⋃ B) ⋃ C (associativa)
- A(BC) = (AB)C (associativa)
- A(B ⋃ C) = AB ⋃ AC (distributiva)
- (A ⋃ B) C = AC ⋃ AB
- ØA = AØ = Ø (aniquiladora)
- {ε}A = A{ε} = A (identidade)
- A ⋃ Ø = Ø ⋃ A = A (identidade)
- A ⋃ A = A (identidade)
- (A*)* = A* (fechamento)
- Ø* = {ε} (fechamento)
- {ε}* = {ε} (fechamento)
As linguagens regulares são fechadas sobre estas operações, isto é, quando alguma das operações for usada sobre uma linguagem regular, o resultado será um conjunto (linguagem) regular.
Um autômato finito mínimo é um DFA com menor número de estados que aceita uma dada linguagem e este autômato é único. Os requisitos para minimização são que o autômato esteja na forma determinística (DFA) e que ele seja completo (transições para todos os símbolos do alfabeto).
O processo de minimização de autômatos tem os seguintes passos:
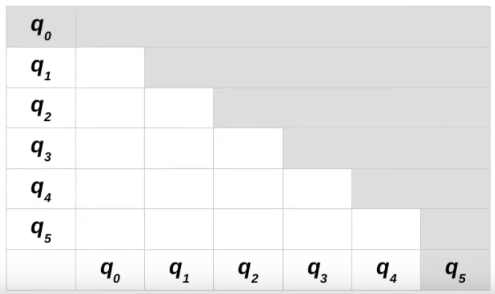
- Construção da tabela.
- A tabela é uma matriz de adjacência, abaixo da diagonal principal
- São eliminados estados iguais e estados redundantes como {q0,q1} = {q1, q0}.
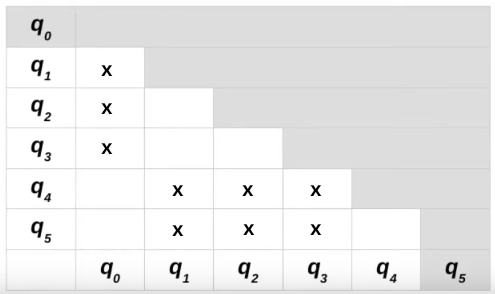
- Marcar estados trivialmente não equivalentes.
- Pares que envolvem um estado final e um não final.
- Marcar estados não equivalentes não triviais.
- Devemos tomar pares não marcados na nossa tabela e compará-los. Tomemos o par hipotético {r1,r2}, devemos olhar suas transições para cada símbolo do alfabeto.
- δ(r1,a)= p1 e δ(r2,a)= p2 .
- Caso p1 = p2, saberemos que r1 e r2 são equivalentes para o símbolo a, mas isso não nos leva a nada ainda.
- Caso p1 != p2.
- se {p1,p2} não está marcado incluímos {q1, q2} na lista do par {p1, p2}.
- se {p1, p2} está marcado devemos marcá-lo e se houver una lista no par {q1,q2} devemos marcar todos pares da lista de maneira recursiva.
- Redesenhar o autômato com a unificação dos estados equivalentes.
- Exclusão de estados inúteis.
- Estados não finais a partir dos quais não se pode chegar a um estado final.
- Exclui-se também as transições que levam a estes estados.
- Este é um passo que nem sempre será necessário.
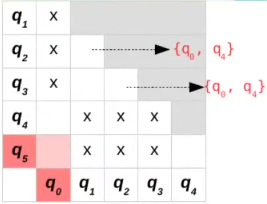
No passo 01 construiremos a tabela:
Após marcarmos os estados trivialmente não equivalentes no passo 2, nossa tabela terá a seguinte configuração:
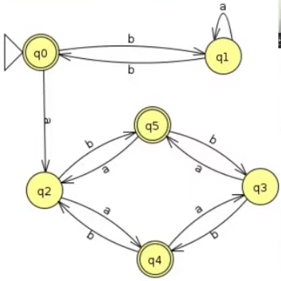
No passo 3 analisaremos caso a caso a mudança de estados que um símbolo gera em cada um dos estados não marcados. Tomemos primeiro q0 e q4:
- δ(q0,a)= q2
- δ(q4,a)= q3
- Dessa comparação temos o par {q2,q3}
- δ(q0,b)= q1
- δ(q4,b)= q2
- Dessa comparação temos o par {q1, q2}
Ambos pares {q2,q3} e {q1,q2} não estão marcados na nossa lista até então e portanto devemos incluir o par que estamos comparando ({q0,q4}) na lista destes pares da seguinte forma:
ignore os pares em vermelho, é difícil fazer isso com prints
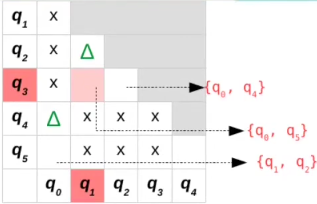
{q0,q5}
- δ(q0,a)= q2
- δ(q5,a)= q2
- Equivalentes em a, não fazemos nada
- δ(q0,b)= q1
- δ(q5,b)= q3
- Incluímos {q0,q5} na lista do estado {q1,q3}
{q1,q2}
- δ(q1,a)= q1
- δ(q2,a)= q4
- Neste caso o par {q1, q4} já está marcado, então q1 e q2 não são equivalentes e devemos marcar este par.
- Além disso, na lista desse par há o par {q0,q4} que deve ser marcado também.
- No par {q0,q4} não há lista, mas se houvesse ela deveria ser marcada.
- δ(q1,b)= q0
- δ(q2,b)= q5
- Incluímos {q1,q2} na lista de {q0,q5}
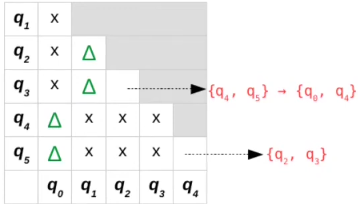
Esta é a nossa tabela até agora:
Note que os pares marcados no passo 3 são indicados pelo triângulo.
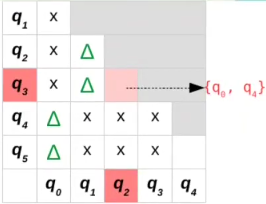
{q1,q3}:
- δ(q1,a)= q1
- δ(q3,a)= q5
- Está marcado, {q1, q3} não são equivalentes e devem ser marcados
- O par {q1,q3} tem em sua lista {q0,q5}, o segundo par é marcado
- O par {q0,q5} tem o par {q1,q2} em sua lista, o terceiro par é marcado
- O par {q1,q2} não tem pares em sua lista, logo a recursão para por aqui
- O par {q0,q5} tem o par {q1,q2} em sua lista, o terceiro par é marcado
- O par {q1,q3} tem em sua lista {q0,q5}, o segundo par é marcado
- Está marcado, {q1, q3} não são equivalentes e devem ser marcados
- δ(q1,b)= q0
- δ(q3,b)= q4
- O par {q0,q4} está marcado e isso indica que {q1,q3} são equivalentes, mais isso já foi aferido.
{q2,q3}:
- δ(q2,a)= q4
- δ(q3,a)= q5
- São diferentes, não estão marcados. Devemos incluir {q2,q3} na lista de {q4,q5}
- δ(q2,b)= q5
- δ(q3,b)= q4
- Mesma coisa que o anterior, segue o baile
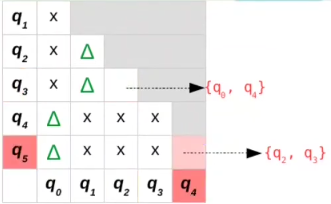
{q4,q5}
- δ(q4,a)= q3
- δ(q5,a)= q2
- {q3,q2} não está marcado, incluímos {q4,q5} em sua lista
- δ(q4,b)= q2
- δ(q5,b)= q3
- Mesma coisa
Nossa tabela final termina da seguinte forma:
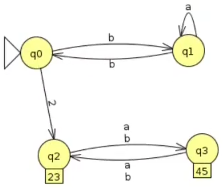
As listas salvas em cada par de estados podem ser ignorados, agora avançamos para o passo 4 de desenhar o autômato com a unificação dos estados não marcados ({q2,q3} e {q4,q5}), ele ficará da seguinte forma:
As gramáticas de tipo 3 são expressas tanto na forma de autômatos finitos, quanto de gramáticas regulares, quanto de expressões regulares. Toda linguagem regular pode ser descrita por uma expressão regular.
Ao operarmos com expressões regulares devemos fazer uso de parênteses como veremos em exemplos adiante, a ordem de precedência dos operadores é: concatenação sucessiva (r⁵), concatenação (rs) e então união (r+s).
Os operadores dentro das expressões regualares são:
- *: Significa 0 ou muitas ocorrências de um símbolo
- ab* significa um símbolo a seguido de 0 ou mais bs.
- +: Significa OU
- (a+b) = a
- (a+b) = b
- (a+b)* = ε
- (a+b)* = a
- (a+b)* = aaaa
- (a+b)* = abbbbb
- (a+b)* = aaabbbaaab
- Pode ser usado como *:
- a+ = a
- a+ = aaaaaa
- Pode ser usado como *:
- Concatenação: normalmente não tem sinal, basta escrever símbolos um ao lado do outro
- ab significa a concatenação de a com b
Se você tiver alguma dúvida, sugestão ou precisar de suporte, por favor, sinta-se à vontade para entrar em contato conosco:
- E-mail: [email protected]
Você também pode criar uma Issue no GitHub para relatar problemas, sugerir melhorias ou contribuir para o desenvolvimento do PET-COLAB. Estamos sempre abertos para receber feedback e colaboração. Obrigado!