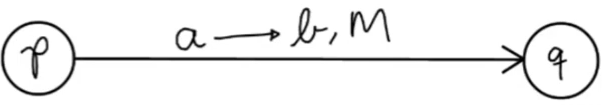Resumo criado pelo aluno João Pedro Trevisan
- CQD-Intro Turing
- CQD-Tese de Turing
- CQD-Maq Turing
- CQD-Mais Turing
- CQD-Variantes Turing
- CQD-Descrevendo Turing
A noção de algoritmo é algo antigo, basicamente provar que existe um conjunto de passos que pode resolver um dado problema é a maneira de se mostrar que este problema é computável, mas é difícil mostrar o que não é computável.
A tese de Church-Turing diz que "tudo aquilo que pode ser calculado é computável", isto é, produzido por uma máquina de Turing. Isso é uma tese e não um teorema pois não se pode provar que é verdade, mas até agora tudo que jogamos nos computadores funcionou, então continuamos assumindo que está certo.
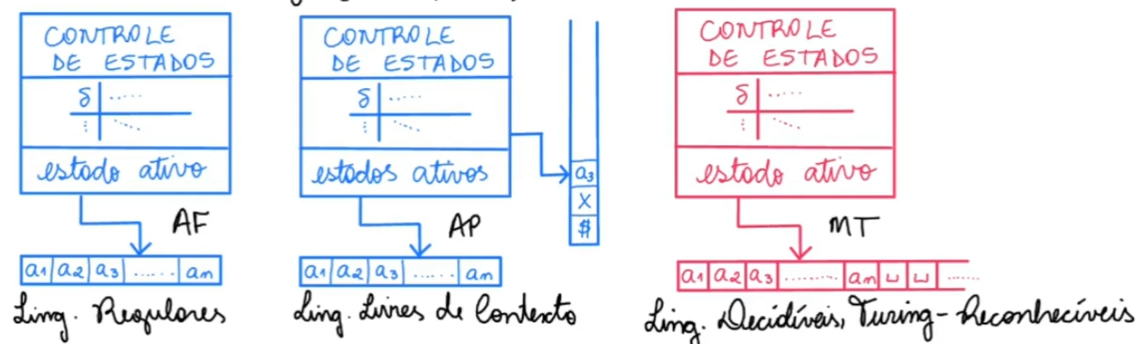
Assim como autômatos finitos e autômatos com pilha, as Máquinas de Turing (MT) são dispositivos reconhecedores. No lugar de uma entrada simples as máquinas de Turing possuem uma fita infinita com símbolos especiais e pode se mover lendo e escrevendo sobre essa fita "andando" para esquerda e para a direita, finalizando ao alcançar um estado de aceitação ou um estado de rejeição.
A notação de transição de uma máquina de Turing é a seguinte:
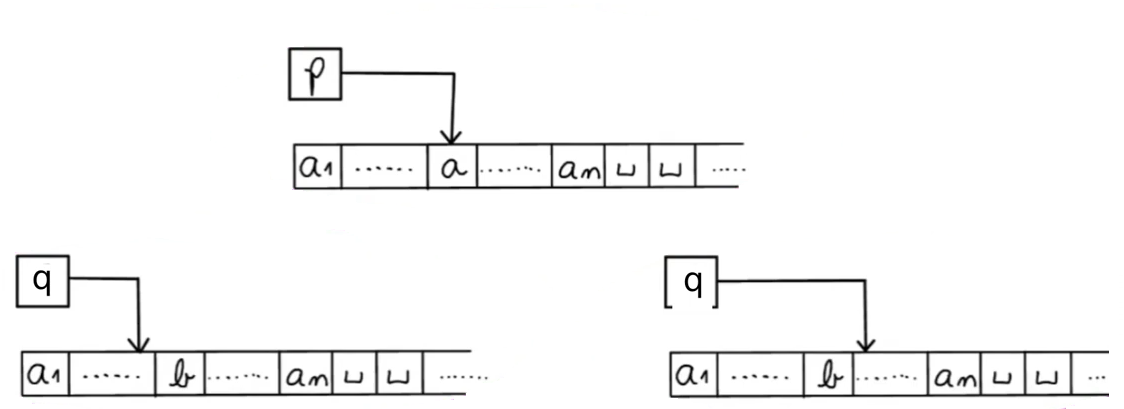
Onde M deve ser substituído por um símbolo que denota "esquerda" ou "direita", geralmente E e D. Isso simboliza que a máquina ao ler um símbolo a escreve na fita um símbolo b e se move para algum dos lados. A imagem a seguir ilustra essa mudança de estados:
É importante ser capaz de visualizar como a MT interage com a fita e isso é mostrado de melhor forma quando se pode ao menos desenhar/escrever e apagar, tornando complicada a exemplificação em um texto. Este vídeo, exemplifica melhor o funcionamento da máquina (veja do momento atual até o fim).
Definindo de uma maneira mais formal, uma MT é uma 7-upla da forma: M = (Q,Σ,Γ,δ,q0,B,F), onde:
- Q = conjunto finito de estados
- Σ = conjunto finito de símbolos de entrada
- Γ = conjunto completo de símbolos de fita
- Σ é sempre um subconjunto de Γ
- δ: Q x Γ → Q x Γ x {E,D}
- Os argumentos de δ(q,X) são um estado q e um símbolo X na fita. O valor de δ(q,X) é uma tripla (p, Y, S) onde p é o próximo estado, Y é o símbolo em Γ gravado na célula sendo lida e S é o sentido no qual se move após esta possível gravação (S = E | D).
- q0 = estado inicial
- B = o símbolo branco
- Este símbolo está em Γ mas não pode estar em Σ.
- O branco aparece inicialmente em todas as células da fita, exceto nas células que contém a entrada
- F = conjunto de estados finais ou de aceitação
Algumas fontes podem usar a notação M = (Q,Σ,Γ,δ,q0,qA,qR), onde o símbolo branco está contido em Γ e qA e qR são respectivamente um conjunto de estados de aceitação e um conjunto de estados de rejeição.
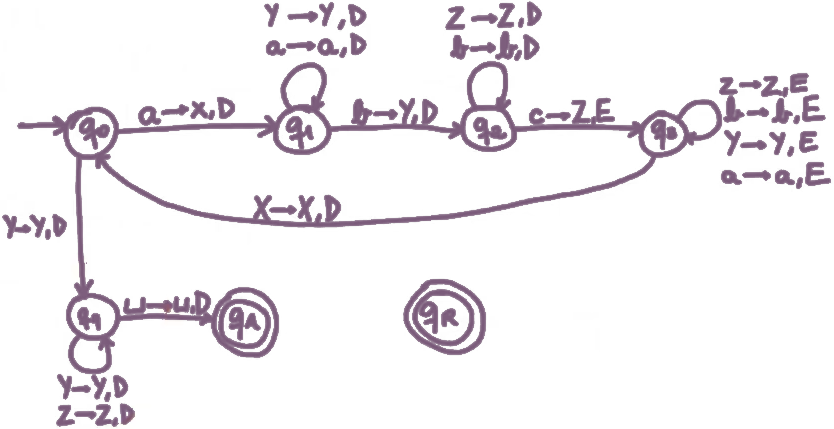
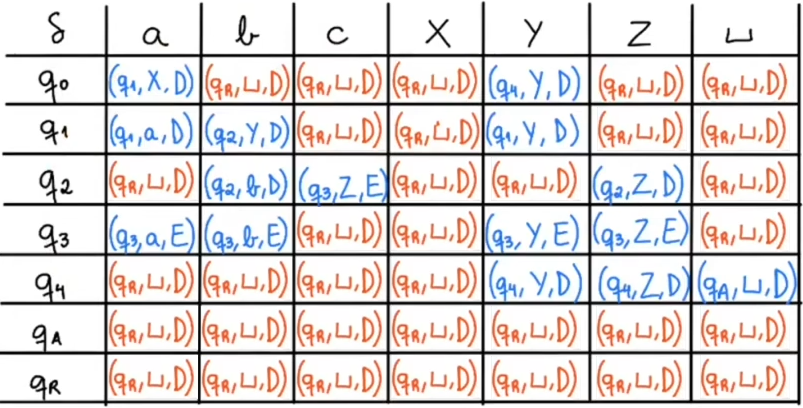
A título de exemplo, vale a pena vermos montada uma máquina de Turing junto de uma tabela de transição de estados, vejamos a máquina:
Perceba que nenhum dos estados aponta diretamente para o estado de rejeição, contudo fica implícito que qualquer movimento inválido leva para ele de forma que a tabela de transição de estados desta MT é a seguinte:
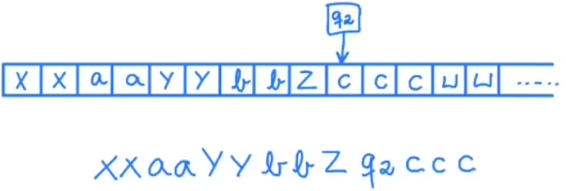
Uma notação importante ao trabalharmos com MTs é a de estado atual, ela tem a forma "αqβ" onde α, β ∈ Γ*, αβ é o conteúdo da fita, q∈Q e a cabeça de leitura está sobre o primeiro símbolo de β.
As gramáticas de autômatos finitos geravam derivações na forma A ->* B que poderiam ter uma série de passos até gerar uma palavra daquela gramática. As máquinas de Turing possuem sequências de configurações que são denotadas da seguinte forma:
Tomemos o estado atual como αxqiyβ:
- Se δ(qi, y) = (qj, z, E), então teremos αxqiyβ ˫ αqjxzβ.
- Como no estado qi a cabeça de leitura está sobre y o símbolo z será escrito sobre ele logo antes de um passo para a esquerda.
- Se δ(qi, y) = (qj, z, D), então teremos αxqiyβ ˫ αxzqjβ.
- Como no estado qi a cabeça de leitura está sobre y o símbolo z será escrito sobre ele logo antes de um passo para a direita.
- Se temos a cabeça de leitura na estrema esquerda da fita uma transição do tipo δ(qi, y) = (qj, z, E) gera uma mudança de estados qiαxyβ ˫ qjzxyβ
- Diferentes autores adotam diferentes abordagens quando a cabeça de leitura está nessa posição e tenta se mover para a esquerda. Alguns adotam o símbolo inicial da fita como um símbolo branco que permite este passo para a esquerda uma vez, outros simplesmente não movem a cabeça de leitura.
Assim como o símbolo ->* denota uma série de derivações que avançam de um estado inicial a algum outro temos o símbolo ˫* que denota uma série indefinida de transições de configuração de uma MT até um determinado estado.
A transição sucessiva de configurações de uma máquina de Turing pode levar a alguns resultados:
- Se ela chega a um estado de aceitação ela (obviamente) aceita a cadeia
- Se ela chega a um estado de aceitação ou rejeição ela decide a cadeia
- Se ela nunca chega a um desses estados ela entrou em loop e a cadeia é indecidível.
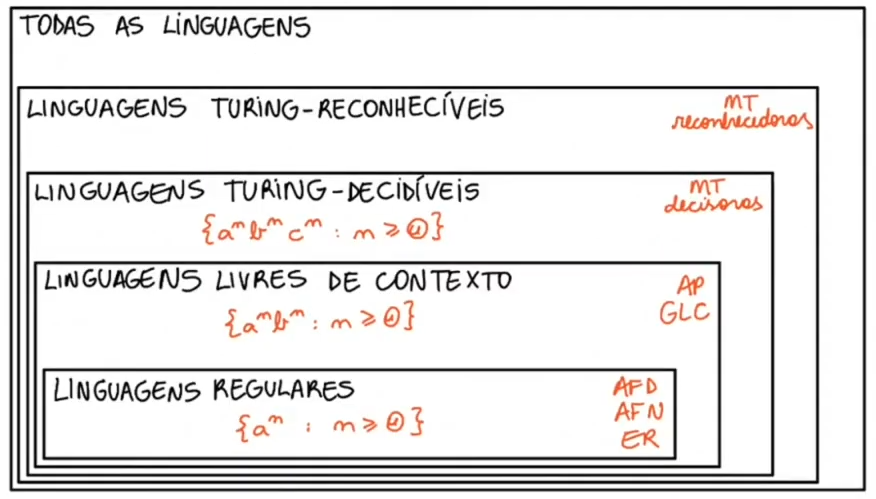
Dito isso, temos duas importantes definições. A primeira delas é a de que uma linguagem é Turing-decidível (ou recursiva) se existe uma MT que a decide. Agora, se existe uma MT que apenas a reconhece esta linguagem é Turing-reconhecível (ou recursivamente enumerável), neste caso a MT aceita entradas pertencentes a linguagem e rejeita ou entra em loop quando não, dito isso, fica claro que o conjunto de linguagens turing-decidíveis está contido dentro do conjunto de linguagens turing-reconhecíveis.
Munidos dessa informação, podemos organizar as linguagens da seguinte forma:
Existem algumas "versões" da máquina de Turing, todas elas implementando algum novo tipo de funcionalidade, contudo, nenhuma delas adiciona nenhum poder computacional. Listaremos as variações e como "corresponder" elas com uma máquina de Turing tradicional.
1. Máquina de Turing que pode ficar parada: Esta MT tem como movimento possível o não movimento, basta realizar dois movimentos opostos seguidos.
2. Máquina de Turing com k Fitas: Com k fitas pode-se ter uma cabeça de leitura/escrita em cada uma das fitas e realizar movimentos em cada uma delas também. Dado que a fita da MT é infinita, pode-se colocar o conteúdo das k fitas em uma única fita, separando-os da forma que queira. A indicação de que as outras cabeças de leitura/escrita deveriam estar em um ponto das fitas virtuais pode ser feita com a indicação de algum símbolo especial. Só levaria mais tempo pois cada passo se tornaria k passos.
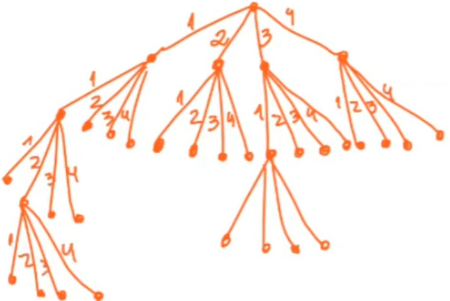
3. Máquina de Turing Não Determinística: Esta é uma máquina que para uma leitura de símbolo em um dado estado pode se mover para mais que um novo estado. Isso faz com que a cada estado escolhido se gere uma série de outros estados possíveis, construindo assim uma árvore. Para simular isso em uma MT tradicional tomamos a maior ramificação possível de um estado para outro, isto é, tomamos um estado q que pode levar a 4 outros estados a título de exemplo.
Para uma MTND como esta montaríamos uma árvore 4-ária pois mesmo que nem todos estados nos deem 4 opções saberemos que nossa árvore real estaria contida nesta árvore 4-ária. A partir de então numeraremos cada um dos ramos desta árvore e usaremos 3 porções da fita da MT tradiconal, na primeira porção armazenamos a entrada original, na segunda o que seria feito sobre esta entrada para cada transição de estado e na terceira armazenaremos o "caminho" sendo feito na árvore.
Realiza-se sobre esta árvore um mergulho em largura em busca de alguma configuração de rejeição ou aceitação.
Para MTNDs se algum ramo entre em configuração de aceitação, aceitamos. Caso todos os ramos entrem em configurações de rejeição, rejeitamos. Caso contrário a computação será infinita.
4. Máquina de Turing com Fita Ilimitada dos Dois Lados: Para simular esta MT com uma MT tradicional podemos usar duas fitas, uma para quando se andaria para a esquerda e outra para a direita. Mas uma MT normal não possui duas fitas, neste caso basta tomarmos a mesma solução que uma MT normal usa para simular uma MT com k fitas.
Se você tiver alguma dúvida, sugestão ou precisar de suporte, por favor, sinta-se à vontade para entrar em contato conosco:
- E-mail: [email protected]
Você também pode criar uma Issue no GitHub para relatar problemas, sugerir melhorias ou contribuir para o desenvolvimento do PET-COLAB. Estamos sempre abertos para receber feedback e colaboração. Obrigado!