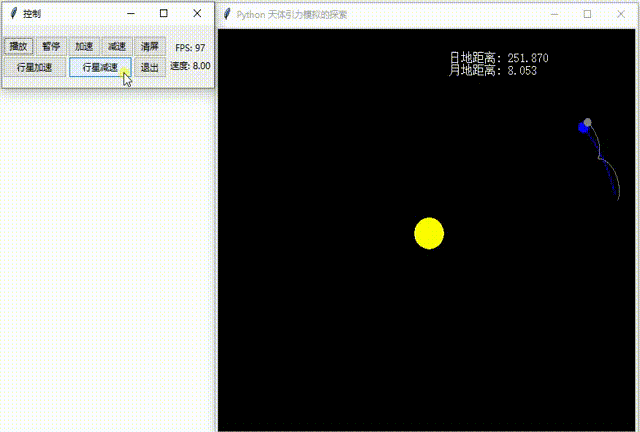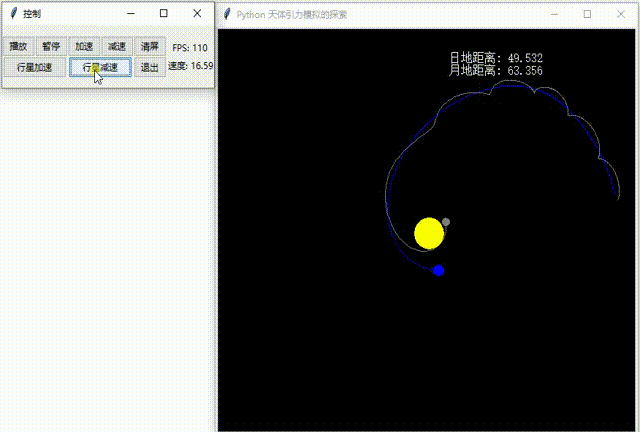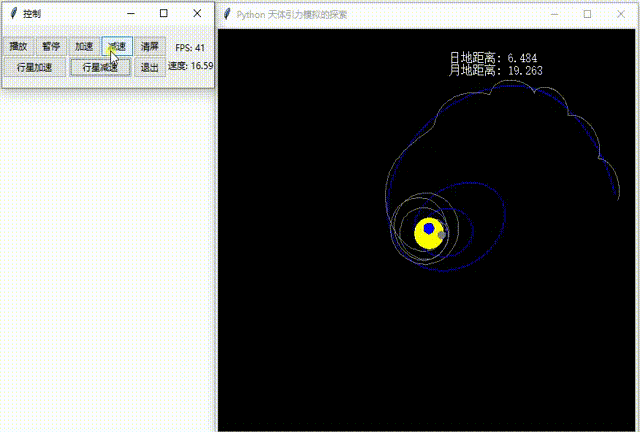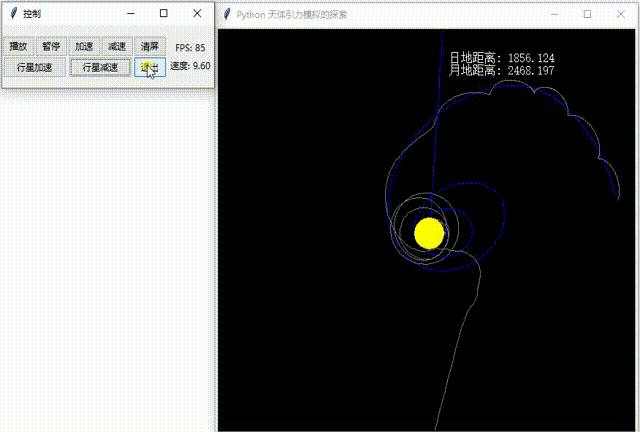
在正式开始之前,先看这两张动图:See the GIFs below before we start.
1.不断减速地球,地球神秘落入太阳中,却自己弹出来?
Slow down the earth continuously. The earth mysteriously falls into the sun, but bounces out?
2.不断增加月球到地球的距离,月球受太阳潮汐力影响,脱离地球?
Increase the distance from the moon to the earth continuously. The moon will be separated from the earth due to the influence of solar tidal force?
这是一个Python计算机模拟万有引力、太阳系行星运动的软件,
应用了万有引力等相关的物理公式计算,可以模拟出天体的椭圆轨道,
以及验证开普勒三大定律,第一、第二宇宙速度。
支持跟踪行星、切换行星,包含简单的发射“飞船”功能。
图形部分使用tkinter(部分结合turtle)或pygame库。
你能在其中创造一个属于自己的宇宙。
此外,这个项目能加以扩展,用来研究其他的物理问题。
This is a software that simulates the gravity and planetary motion in the universe with Python,
using physical formulas including universal gravitation to calculate the orbits of celestial bodies
and verifying Kepler's three laws and the first and second cosmic velocities.
It supports tracking, switching planets and launching simple "spaceships",
with module tkinter (partially combined with turtle) or pygame for graphics.
You're able to create a universe belonging to yourself in this program.
Additionally, this project can be further extended to research other physical problems.
The English introduction is placed below the Chinese version.
项目源代码 (Project source code):https://github.com/qfcy/python-gravity-simulator
源代码位于solar_system目录中。
solar_system.py:主程序的最新版本,也是一个公共的模块
solar_system_v1.0.py:主程序的1.0版本(存档备用)
solar_system_v1.1.1.py:主程序的1.1.1版本(存档备用)
solar_system_v1.2.04.py:主程序的1.2.04版本(存档备用)
empty.pkl和spacecraft.pkl:solar_system.py使用pickle库存储天体数据,这是天体数据的两个备用模板。(empty.pkl为空的宇宙,spacecraft.pkl是仅有一对飞船的宇宙。)
(一部分是用来测试的)
TESTs/solar_system_accelerate.py:使用C语言扩展提升计算的性能(经作者测试,与solar_system.py相比,速度约提升22~45倍),并增加了二阶龙格库塔法
TESTs/solar_system_particles.py:使用更快的“粒子”计算小行星,用于提升计算性能(备用)
TESTs/solar_system_blackhole1.py:行星掉入黑洞的模拟1
TESTs/solar_system_blackhole2.py:行星掉入黑洞的模拟2,包含对turtle模块函数的修改和补丁,如turtle模块绘制旋转图片(见 这篇文章)
TESTs/solar_system_blackhole3.py:第3个行星掉入黑洞的模拟
TESTs/solar_system_hill_sphere.py:希尔球、拉格朗日点 现象模拟。希尔球指卫星到行星的距离不能超过最大值,也就是前面的第二张动图
TESTs/solar_system_binary_star.py:双星系统模拟
TESTs/solar_system_collision1.py:太阳系行星形成粗略模拟,应用了行星的碰撞反弹算法 (参见这篇文章)
TESTs/solar_system_collision2.py:行星的碰撞反弹算法测试
TESTs/solar_system_molecule.py:分子间作用力的"粗略"模拟
TESTs/solar_system_debug.py:输出调试信息,如程序中单次计算、双精度浮点数导致的精度损失等
教具版:验证开普勒第一、第二、第三定律、第一、二宇宙速度和模拟卫星的变轨,并含有作者编写这个程序的实践报告,和教具的各个早期版本存档。
pygame:使用pygame库的实现(待完善)
dist:使用pyinstaller的打包exe文件,及用Inno Setup制作的安装包。
开始编程前,研究真实的物理问题,首先要对物理问题涉及的研究对象进行抽象与建模。
在真实的宇宙中,天体与其他各个天体之间都存在引力。
为简化研究,程序使用“降维”的思想,将真实的三维宇宙转换为二维的宇宙。
宇宙的本身属性引力常量G使用一个常量表示。每一个行星可以表示为它的质量、速度、x坐标、y坐标的属性。
天体轨迹的计算
程序应用微分的方法,将天体的运行分解为许多步微小的直线运动。通过重复计算天体每一步的移动,就能得到天体的运行轨迹。
假设有两个天体A,B,则引力为F = GMm/r^2^ ,天体之间的距离为 d=sqrt( (xA-xB)^2^+(yA-yB)^2^),
天体A在x方向上的加速度为ax = F/m = F |xA - xB|/md ,在y方向上的加速度为ay = F/m = F |yA - yB| /md。
设程序单步经历的时间为t,则应用欧拉法得出,新一轮天体A速度v=v0+at,位移x=x0+vt。
程序这样重复这一个计算,不断地循环,就能逼真地模拟天体的运动过程。t越小,模拟越精确。
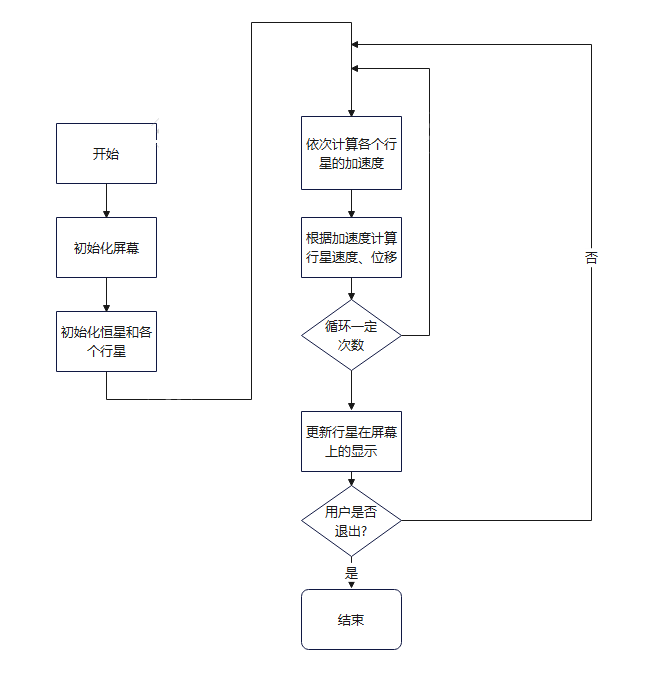
程序首先初始化屏幕、恒星和各个行星,
然后重复一个不断计算和绘制的事件循环。在这个循环中:
1.计算行星受到重力合力的加速度。
2.计算速度和位移。
3.重复1、2步骤若干次。
4.调用turtle模块中的函数,绘制行星到屏幕上。
流程图是这个样子:
关于更详细的程序原理,请看“开普勒定律\程序原理(文章)”这个文件夹。
本项目曾获多个信息技术奖项,证书这里就不展示了。
不过,仓库里面有获奖作品的申报材料,留给需要做信息技术竞赛的同学做参考。
Q: 为什么本项目结合使用了tkinter和turtle,而不直接使用tkinter,或其他图形库渲染图形?
A: 首先,作者本想用tkinter库编写该程序,但考虑到直接调用Canvas控件绘制行星形状的代码量较大,而且基于tkinter的turtle库封装了tkinter,能够间接调用Canvas控件进行绘图,就使用turtle库绘制图形,避免重复造轮子。
目前,程序中的界面主要使用tkinter库设计,而基于tkinter的turtle库仅用于渲染。另外,作者基于自己的tkinter知识,重写和扩展了原版turtle模块,如TESTS\solar_system_blackhole2.py基于PIL库为turtle添加了图像旋转功能。
其次,使用turtle库可减少图形渲染的代码,将主要精力用于物理算法的设计,以及其他功能的开发上。
Q: 程序的计算有哪些已知的误差?
A: 程序中的计算精度由两个因素影响:微分的精细度,也就是单次计算经过的时间间隔(dt),以及双精度浮点数精度误差。具体参见TESTS\solar_system_debug.py中的介绍。
2021年开始编写该程序时,作者尚是一位高中生。
作者CSDN主页:qfcy_
bilibili主页:qfcy_
英文版介绍(使用了翻译软件+自己修改、润色):
The source code is located in the solar_system directory.
solar_system.py: The latest version of the main program that also serves as a utility module
solar_system_v1.0.py: Version 1.0 of the main program (archive)
solar_system_v1.1.1.py: Version 1.1.1 of the main program (archive)
solar_system_v1.2.04.py: Version 1.2.04 of the main program (archive)
empty.pkl and spacecraft.pkl: As file "solar_system.py" uses module pickle to store datas, these are the examples for the storage of celestial data. (empty.pkl is an empty universe, and spacecraft.pkl is a universe with only a pair of spacecraft.)
(Part of it is for tests or just for fun)
TESTs/solar_system_accelerate.py: Using C extension to improve the performance of calculations (according to the author's test, the speed is about 22 to 45 times faster compared with solar_system.py), and adding the second-order Runge-Kutta method.
TESTs/solar_system_particles.py: Using faster "particles" to calculate the movement of asteroids to improve the performance.(standby)
TESTs/solar_system_blackhole1.py: The first version of simulations of planets falling into black holes.
TESTs/solar_system_blackhole2.py: The second version of simulations of planets falling into black holes. (including the technique of drawing rotating pictures with turtle module, see this article)
TESTs/solar_system_blackhole3.py: The third version of simulations of planets falling into black holes.
TESTs/solar_system_hill_sphere.py: Hill Sphere and Lagrange Point simulation. Hill Sphere refers to that the distance from a satellite to a planet cannot exceed the maximum value (same as the second GIF at the beginning).
TESTs/solar_system_binary_star.py: Binary star system simulation
TESTs/solar_system_collision1.py: A rough simulation of the formation of planets in the solar system, using the collision-rebound algorithm (see this article)
TESTs/solar_system_collision2.py: A test of collision-rebound algorithm
TESTs/solar_system_molecule.py: A "rough" simulation of intermolecular forces
TESTs/solar_system_debug.py: Debug information outputing, such as the precision loss in a single calculation or caused by double-precision floating-point numbers
ENG: The English localized version, also containing the simulation of verifying Kepler's three laws, first and second cosmic velocities and satellite orbit adjustment.
pygame: An implementation using pygame library (TODO: to be improved).
ENG\dist: Packaged executable files with pyinstaller and the setup program with Inno Setup.
Before starting programming, you need to abstract and model the research objects involved in physical problems before studying real physical problems.
In the real universe, there is gravity between celestial bodies and other celestial bodies.
To simplify the research, the program uses the idea of "dimension reduction" to convert the real three-dimensional universe into a two-dimensional universe.
The gravitational constant G of the universe is expressed as a constant. Each planet can be described as its mass, speed, x coordinate, y coordinate attributes.
The calculation of trajetories
The program uses the method of differentiation to divide the motions of celestial bodies into many steps of tiny linear motion. By repeating the calculation of each step of the celestial body's movement, the trajectory of the celestial body can be obtained.
Suppose there are two celestial bodies A and B, then the gravity is F = GMm/r^2^, and the distance between celestial bodies is d=sqrt( (xA-xB)^2^+(yA-yB)^2^).
The acceleration of celestial body A in the x direction is ax = F/m = F |xA - xB|/md. As for the y direction, the acceleration is ay = F/m = F |yA - yB|/md.
If the time of single step of the program is t, using Eulerian method, the new velocity of celestial body A is v=v0+at and the displacement is x=x0+vt.
In this way, the program repeats this calculation and keeps looping, so that it can realistically simulate the motion process of celestial bodies. The t smaller, the more accurate the simulation.
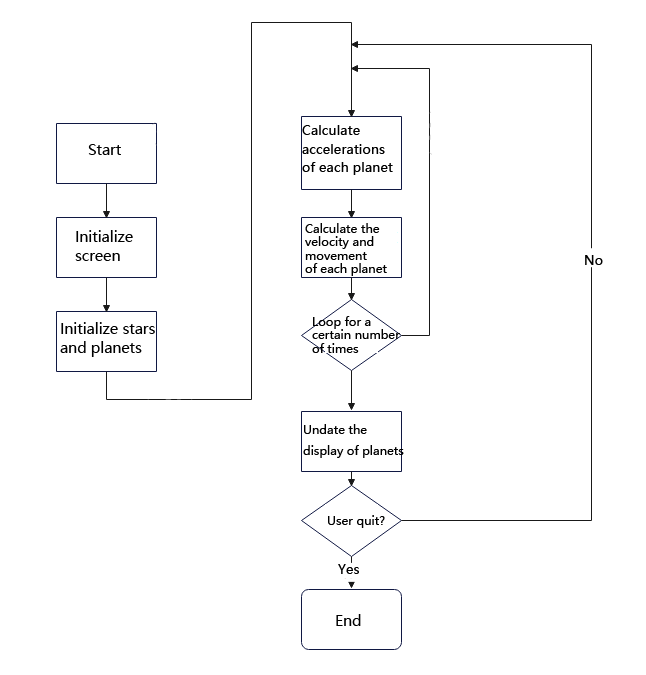
The program firstly initializes the screen, stars and planets,
Then repeat an event cycle that is continuously calculated and drawn. In this cycle:
- Calculate the acceleration of the planet under the combined force of gravity.
- Calculate the speed and displacement.
- Repeat steps 1 and 2 several times.
- Call the function in the title module to draw the planet on the screen.
The brief flow chart is as follows:
For more detailed principles of this program in Chinese, see the folder "开普勒定律\程序原理(文章)".
This project has won many awards in IT competitions in China, but I won't show the certificates.
However, there are application materials for award-winning works in the repository for students who need to participate in other IT competitions.
Q: Why does this project combine the use of tkinter and turtle, rather than using tkinter alone or other libraries for rendering?
A: Initially, I intended to use the tkinter module to write the program, but considering the substantial amount of code required to directly manipulate the Canvas widget for drawing planetary shapes, while the turtle module based on tkinter encapsulates many tkinter functions and can indirectly invoke the Canvas widget for drawing, the turtle module was chosen for rendering to avoid reinventing wheels.
Currently, the program's interface is mainly designed using the tkinter module, while the turtle module, which is based on tkinter, is only used for rendering. Additionally, I has rewritten and extended the original turtle module based on their knowledge of tkinter, such as adding image rotation functionality to turtle using the PIL library in TESTS\solar_system_blackhole2.py.
Furthermore, using the turtle module reduces the amount of code needed for graphic rendering, allowing the main focus to be on designing the physics algorithms and developing other features.
Q: What are the known factors contributing to the precision loss in calculations?
A: The accuracy of the computations in the program is influenced by two factors: the granularity of the differentiation, i.e., the time interval (dt) per computation, and the precision errors of double-precision floating-point numbers. For more details, see the description in TESTS\solar_system_debug.py(in Chinese).
When the development of the program started in 2021, the author was still a high school student.
GitHub home page: qfcy_
CSDN home page: qfcy_
Bilibili home page: qfcy_