Topics:
- Queues
- Doubly Linked Lists
- Binary Search Trees
- Heaps
Stretch Goals:
- Generic Heaps
- AVL Trees
- LRU Caches
-
Implement each data structure, starting with the queue. Make sure you're in the approriate directory, then run
python3 test_[NAME OF DATA STRUCTURE].pyto run the tests for that data structure and check your progress. Get all the tests passing for each data structure. -
Open up the
Data_Structures_Questions.mdfile, which asks you to evaluate the runtime complexity of each of the methods you implemented for each data structure. Add your answers to each of the questions in the file.
NOTE: The quickest and easiest way to reliably import a file in Python is to just copy and paste the file you want to import into the same directory as the file that wants to import. This obviously isn't considered best practice, but it is the most reliable way to do it across all platforms.
- Should have the methods:
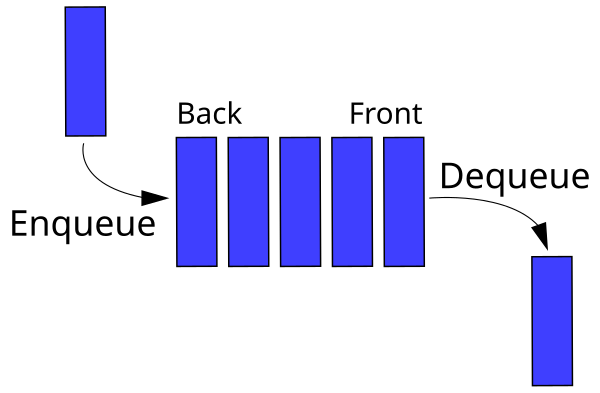
enqueue,dequeue, andlen.enqueueshould add an item to the back of the queue.dequeueshould remove and return an item from the front of the queue.lenreturns the number of items in the queue.
- The
ListNodeclass, which represents a single node in the doubly-linked list, has already been implemented for you. Inspect this code and try to understand what it is doing to the best of your ability. - The
DoublyLinkedListclass itself should have the methods:add_to_head,add_to_tail,remove_from_head,remove_from_tail,move_to_front,move_to_end,delete, andget_max.add_to_headreplaces the head of the list with a new value that is passed in.add_to_tailreplaces the tail of the list with a new value that is passed in.remove_from_headremoves the head node and returns the value stored in it.remove_from_tailremoves the tail node and returns the value stored in it.move_to_fronttakes a reference to a node in the list and moves it to the front of the list, shifting all other list nodes down.move_to_endtakes a reference to a node in the list and moves it to the end of the list, shifting all other list nodes up.deletetakes a reference to a node in the list and removes it from the list. The deleted node'spreviousandnextpointers should point to each afterwards.get_maxreturns the maximum value in the list.
- The
headproperty is a reference to the first node and thetailproperty is a reference to the last node.
- Should have the methods
insert,contains,get_max.insertadds the input value to the binary search tree, adhering to the rules of the ordering of elements in a binary search tree.containssearches the binary search tree for the input value, returning a boolean indicating whether the value exists in the tree or not.get_maxreturns the maximum value in the binary search tree.for_eachperforms a traversal of every node in the tree, executing the passed-in callback function on each tree node value. There is a myriad of ways to perform tree traversal; in this case any of them should work.
- Should have the methods
insert,delete,get_max,_bubble_up, and_sift_down.insertadds the input value into the heap; this method should ensure that the inserted value is in the correct spot in the heapdeleteremoves and returns the 'topmost' value from the heap; this method needs to ensure that the heap property is maintained after the topmost element has been removed.get_maxreturns the maximum value in the heap in constant time.get_sizereturns the number of elements stored in the heap._bubble_upmoves the element at the specified index "up" the heap by swapping it with its parent if the parent's value is less than the value at the specified index._sift_downgrabs the indices of this element's children and determines which child has a larger value. If the larger child's value is larger than the parent's value, the child element is swapped with the parent.
A max heap is pretty useful, but what's even more useful is to have our heap be generic such that the user can define their own priority function and pass it to the heap to use.
Augment your heap implementation so that it exhibits this behavior. If no comparator function is passed in to the heap constructor, it should default to being a max heap. Also change the name of the get_max function to get_priority.
You can test your implementation against the tests in test_generic_heap.py. The test expects your augmented heap implementation lives in a file called generic_heap.py. Feel free to change the import statement to work with your file structure or copy/paste your implementation into a file with the expected name.
An AVL tree (Georgy Adelson-Velsky and Landis' tree, named after the inventors) is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property.
We define balance factor for each node as :
balanceFactor = height(left subtree) - height(right subtree)
The balance factor of any node of an AVL tree is in the integer range [-1,+1]. If after any modification in the tree, the balance factor becomes less than −1 or greater than +1, the subtree rooted at this node is unbalanced, and a rotation is needed.
Implement an AVL Tree class that exhibits the aforementioned behavior. The tree's insert method should perform the same logic as what was implemented for the binary search tree, with the caveat that upon inserting a new element into the tree, it will then check to see if the tree needs to be rebalanced.
How does the time complexity of the AVL Tree's insertion method differ from the binary search tree's?
An LRU (Least Recently Used) cache is an in-memory storage structure that adheres to the Least Recently Used caching strategy.
In essence, you can think of an LRU cache as a data structure that keeps track of the order in which elements (which take the form of key-value pairs) it holds are added and updated. The cache also has a max number of entries it can hold. This is important because once the cache is holding the max number of entries, if a new entry is to be inserted, another pre-existing entry needs to be evicted from the cache. Because the cache is using a least-recently used strategy, the oldest entry (the one that was added/updated the longest time ago) is removed to make space for the new entry.
So what operations will we need on our cache? We'll certainly need some sort of set operation to add key-value pairs to the cache. Newly-set pairs will get moved up the priority order such that every other pair in the cache is now one spot lower in the priority order that the cache maintains. The lowest-priority pair will get removed from the cache if the cache is already at its maximal capacity. Additionally, in the case that the key already exists in the cache, we simply want to overwrite the old value associated with the key with the newly-specified value.
We'll also need a get operation that fetches a value given a key. When a key-value pair is fetched from the cache, we'll go through the same priority-increase dance that also happens when a new pair is added to the cache.
Note that the only way for entries to be removed from the cache is when one needs to be evicted to make room for a new one. Thus, there is no explicit remove method.
Given the above spec, try to get a working implementation that passes the tests. What data structure(s) might be good candidates with which to build our cache on top of? Hint: Since our cache is going to be storing key-value pairs, we might want to use a structure that is adept at handling those.
Once you've gotten the tests passing, it's time to analyze the runtime complexity of your get and set operations. There's a way to get both operations down to sub-linear time. In fact, we can get them each down to constant time by picking the right data structures to use.
Here are you some things to think about with regards to optimizing your implementation: If you opted to use a dictionary to work with key-value pairs, we know that dictionaries give us constant access time, which is great. It's cheap and efficient to fetch pairs. A problem arises though from the fact that dictionaries don't have any way of remembering the order in which key-value pairs are added. But we definitely need something to remember the order in which pairs are added. Can you think of some ways to get around this constaint?