Level_2_solutions.md

Test 1 adjacentElementsProduct

Given an array of integers, find the pair of adjacent elements that has the largest product and return that product.

Example

For inputArray = [3, 6, -2, -5, 7, 3], the output should be adjacentElementsProduct(inputArray) = 21. 7 and 3 produce the largest product.

Input/Output

• [time limit] 4000ms (py)
• [input] array.integer inputArray: An array of integers containing at least two elements. Guaranteed constraints: 2 ≤ inputArray.length ≤ 10, -1000 ≤ inputArray[i] ≤ 1000.
• [output] integer: The largest product of adjacent elements.

def adjacentElementsProduct(inputArray):
    ll = [x*y for (x,y) in zip(inputArray[:-1], inputArray[1:])]
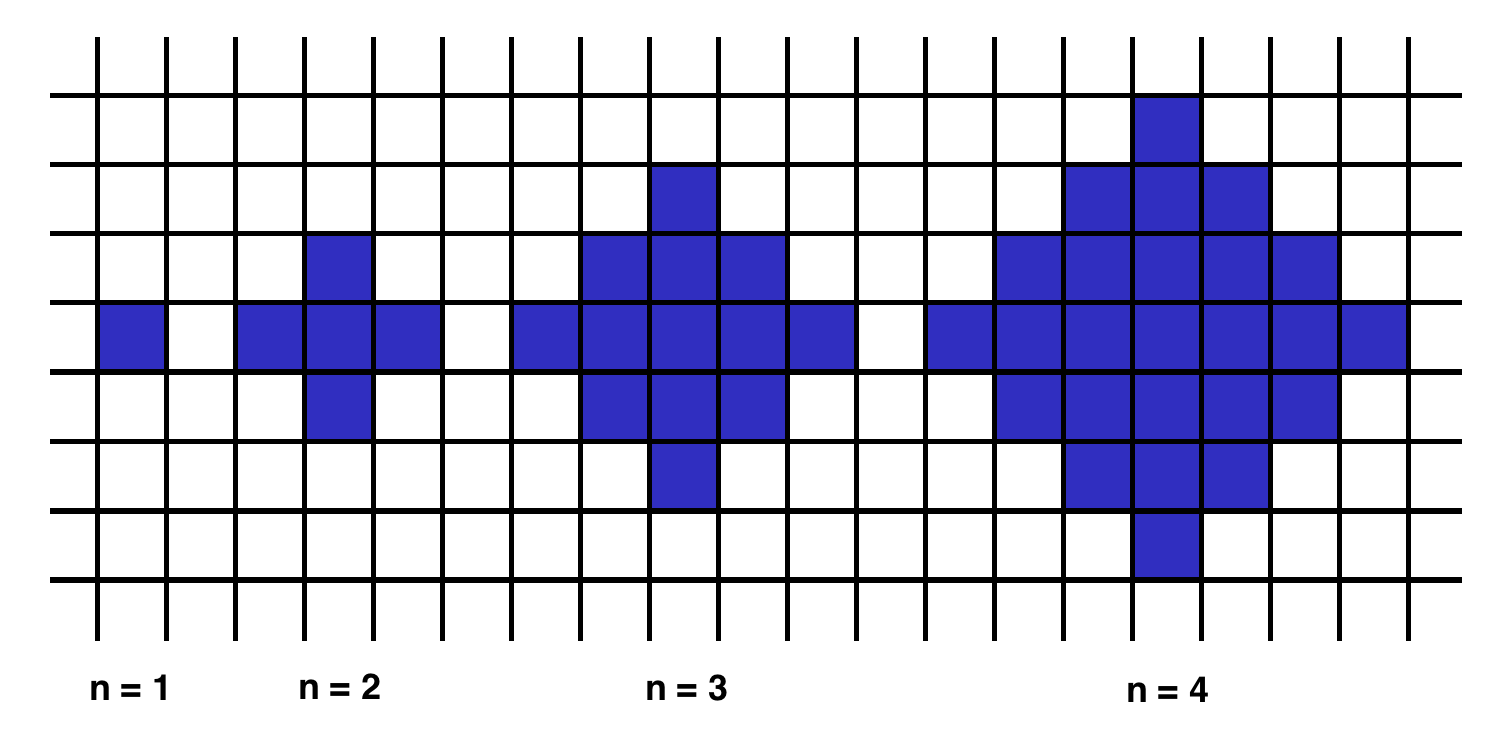
    return max(ll)

Test 2 shapeArea

Below we will define an n-interesting polygon. Your task is to find the area of a polygon for a given n. A 1-interesting polygon is just a square with a side of length 1. An n-interesting polygon is obtained by taking the n - 1-interesting polygon and appending 1-interesting polygons to its rim, side by side. You can see the 1-, 2-, 3- and 4-interesting polygons in the picture below.

Example

For n = 2, the output should be shapeArea(n) = 5; For n = 3, the output should be shapeArea(n) = 13.

Input/Output

• [time limit] 4000ms (py)
• [input] integer n: Guaranteed constraints: 1 ≤ n < 104.
• [output] integer: The area of the n-interesting polygon.

def shapeArea(n):
    area = 1
    while n>1:
        area += (n-1)*4
        n -=1
    return area

Test 3 makeArrayConsecutive2

Ratiorg got statues of different sizes as a present from CodeMaster for his birthday, each statue having an non-negative integer size. Since he likes to make things perfect, he wants to arrange them from smallest to largest so that each statue will be bigger than the previous one exactly by 1. He may need some additional statues to be able to accomplish that. Help him figure out the minimum number of additional statues needed.

Example

For statues = [6, 2, 3, 8], the output should be makeArrayConsecutive2(statues) = 3. Ratiorg needs statues of sizes 4, 5 and 7.

Input/Output

• [time limit] 4000ms (py)
• [input] array.integer statues: An array of distinct non-negative integers. Guaranteed constraints:1 ≤ statues.length ≤ 10, 0 ≤ statues[i] ≤ 20.
• [output] integer: The minimal number of statues that need to be added to existing statues such that it contains every integer size from an interval [L, R] (for some L, R) and no other sizes.

def makeArrayConsecutive2(statues):
    statues.sort()
    if len(statues) > 1:
        diff_statues = [y-x for x, y in zip(statues[:-1], statues[1:])]
        return sum(i-1 for i in diff_statues)
    else:
        return 0

Test 4 almostIncreasingSequence:

Given a sequence of integers as an array, determine whether it is possible to obtain a strictly increasing sequence by removing no more than one element from the array.

Example

For sequence = [1, 3, 2, 1], the output should be almostIncreasingSequence(sequence) = false; There is no one element in this array that can be removed in order to get a strictly increasing sequence. For sequence = [1, 3, 2], the output should be almostIncreasingSequence(sequence) = true.

You can remove 3 from the array to get the strictly increasing sequence [1, 2]. Alternately, you can remove 2 to get the strictly increasing sequence [1, 3].

Input/Output

• [time limit] 4000ms (py)
• [input] array.integer sequence: Guaranteed constraints: 2 ≤ sequence.length ≤ 105, -105 ≤ sequence[i] ≤ 105.
• [output] boolean: Return true if it is possible to remove one element from the array in order to get a strictly increasing sequence, otherwise return false.

def almostIncreasingSequence(sequence):
    dff_seq = [x>=y for x, y in zip(sequence[:-1], sequence[1:])]
    if sum(dff_seq) >=2:
        return False
    elif sum(dff_seq) == 0:
        return True
    else:
        ind = dff_seq.index(True)
        t_seq = list(sequence);
        t_seq.pop(ind+1)
        dff_seq1 = [x>=y for x, y in zip(t_seq[:-1], t_seq[1:])]
        t_seq = list(sequence);
        t_seq.pop(ind)
        dff_seq2 = [x>=y for x, y in zip(t_seq[:-1], t_seq[1:])]
        return sum(dff_seq1)<1 or sum(dff_seq2)<1

Test 5 matrixElementsSum

After becoming famous, CodeBots decided to move to a new building and live together. The building is represented by a rectangular matrix of rooms, each cell containing an integer - the price of the room. Some rooms are free (their cost is 0), but that's probably because they are haunted, so all the bots are afraid of them. That is why any room that is free or is located anywhere below a free room in the same column is not considered suitable for the bots. Help the bots calculate the total price of all the rooms that are suitable for them.

Example

For matrix = [[0, 1, 1, 2], [0, 5, 0, 0], [2, 0, 3, 3]], the output should be matrixElementsSum(matrix) = 9.

Here's the rooms matrix with unsuitable rooms marked with 'x': [[x, 1, 1, 2], [x, 5, x, x], [x, x, x, x]] Thus, the answer is 1 + 5 + 1 + 2 = 9.

Input/Output

• [time limit] 4000ms (py)
• [input] array.array.integer matrix: 2-dimensional array of integers representing a rectangular matrix of the building. Guaranteed constraints: 1 ≤ matrix.length ≤ 5, 1 ≤ matrix[i].length ≤ 5, 0 ≤ matrix[i][j] ≤ 10.
• [output] integer

def matrixElementsSum(matrix):
    costSum = 0
    for x in range(len(matrix)):
        for y in range(len(matrix[0])):
            if x>0:
                if matrix[x-1][y] == 0:
                    matrix[x][y] = 0
            costSum += matrix[x][y]
    return costSum