README.md

2476.二叉搜索树最近节点查询

难度：中等

题目

给你一个 二叉搜索树 的根节点 root ，和一个由正整数组成、长度为 n 的数组 queries 。

请你找出一个长度为 n 的 二维 答案数组 answer ，其中 answer[i] = [mini, maxi] ：

mini 是树中小于等于 queries[i] 的 最大值 。如果不存在这样的值，则使用 -1 代替。 maxi 是树中大于等于 queries[i] 的 最小值 。如果不存在这样的值，则使用 -1 代替。 返回数组 answer 。

示例

示例 1 ：

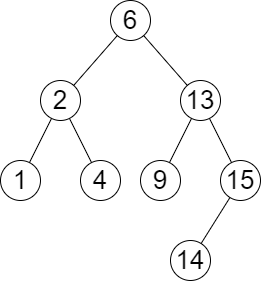
输入：root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
输出：[[2,2],[4,6],[15,-1]]
解释：按下面的描述找出并返回查询的答案：
- 树中小于等于 2 的最大值是 2 ，且大于等于 2 的最小值也是 2 。所以第一个查询的答案是 [2,2] 。
- 树中小于等于 5 的最大值是 4 ，且大于等于 5 的最小值是 6 。所以第二个查询的答案是 [4,6] 。
- 树中小于等于 16 的最大值是 15 ，且大于等于 16 的最小值不存在。所以第三个查询的答案是 [15,-1] 。

示例 2 ：

输入：root = [4,null,9], queries = [3]
输出：[[-1,4]]
解释：树中不存在小于等于 3 的最大值，且大于等于 3 的最小值是 4 。所以查询的答案是 [-1,4] 。

提示：

树中节点的数目在范围 [2, 105] 内
1 <= Node.val <= 106
n == queries.length
1 <= n <= 105
1 <= queries[i] <= 106

题解

import { type TreeNode } from '../../utils/TreeNode'

/**
 * @description: 时间复杂度 O(N + QlgQ) 空间复杂度 O(N) N: 节点数量 Q: queries 长度
 * @return {*}
 * @param {TreeNode} root
 * @param {number} queries
 */
export function closestNodes(root: TreeNode | null, queries: number[]): number[][] {
    const orderTree: number[] = []
    getMiddleOrderTree(root, orderTree)
    return queries.map(query => {
        const index = findNearestItem(orderTree, query)
        const left = orderTree[index] || -1
        if (left === query) {
            return [left, left]
        }
        const right = orderTree[index + 1] || -1
        return [left, right]
    })
}

function getMiddleOrderTree(root: TreeNode | null, orderTree: number[]) {
    if (!root) return
    getMiddleOrderTree(root.left, orderTree)
    orderTree.push(root.val)
    getMiddleOrderTree(root.right, orderTree)
}

function findNearestItem(orderTree: number[], target: number) {
    let left = -1
    let right = orderTree.length - 1
    while (left < right) {
        const mid = (left + right + 1) >> 1
        const cur = orderTree[mid]
        if (cur === target) {
            return mid
        }
        if (cur > target) {
            right = mid - 1
        }
        else {
            left = mid
        }
    }
    return left
}