背包问题完全背包一维.md

完全背包-一维数组

本题力扣上没有原题，大家可以去卡码网第52题去练习。

算法公开课

《代码随想录》算法视频公开课：带你学透完全背包问题！ ，相信结合视频再看本篇题解，更有助于大家对本题的理解。

思路

本篇我们不再做五部曲分析，核心内容 在 01背包二维 、01背包一维 和 完全背包二维 的讲解中都讲过了。

上一篇我们刚刚讲了完全背包二维DP数组的写法：

for (int i = 1; i < n; i++) { // 遍历物品
    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
    }
}

压缩成一维DP数组，也就是将上一层拷贝到当前层。

将上一层dp[i-1] 的那一层拷贝到 当前层 dp[i] ，那么 递推公式由：dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]) 变成： dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i])

这里有录友想，这样拷贝的话， dp[i - 1][j] 的数值会不会 覆盖了 dp[i][j] 的数值呢？

并不会，因为 当前层 dp[i][j] 是空的，是没有计算过的。

变成 dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]) 我们压缩成一维dp数组，去掉 i 层数维度。

即：dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

接下来我们重点讲一下遍历顺序。

看过这两篇的话：

• 01背包理论基础（二维数组）
• 01背包理论基础（一维数组）

就知道了，01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。

在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！

因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。

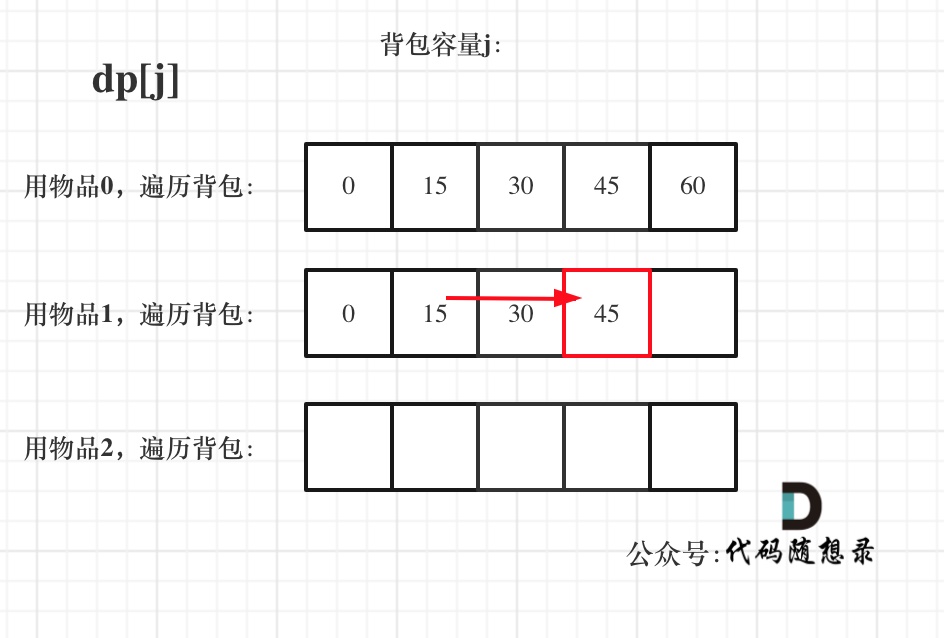
遍历物品在外层循环，遍历背包容量在内层循环，状态如图：

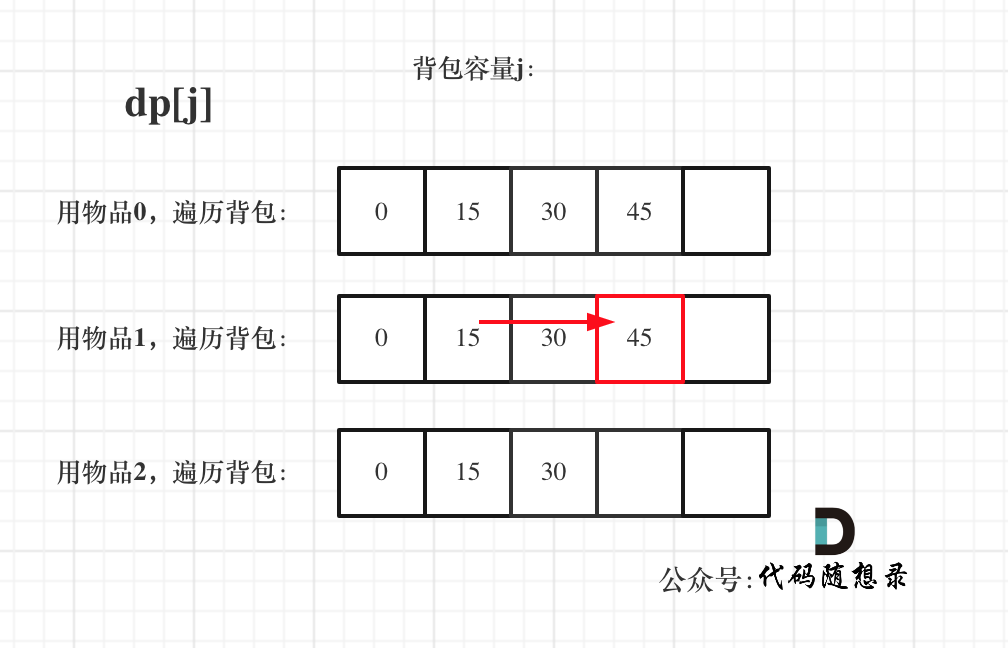
遍历背包容量在外层循环，遍历物品在内层循环，状态如图：

看了这两个图，大家就会理解，完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值（这个值就是下标j之前所对应的dp[j]）。

先遍历背包再遍历物品，代码如下：

for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
    cout << endl;
}

先遍历物品再遍历背包：

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

整体代码如下：

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int N, bagWeight;
    cin >> N >> bagWeight;
    vector<int> weight(N, 0);
    vector<int> value(N, 0);
    for (int i = 0; i < N; i++) {
        int w;
        int v;
        cin >> w >> v;
        weight[i] = w;
        value[i] = v;
    }

    vector<int> dp(bagWeight + 1, 0);
    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
        for(int i = 0; i < weight.size(); i++) { // 遍历物品
            if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;

    return 0;
}

总结

细心的同学可能发现，全文我说的都是对于纯完全背包问题，其for循环的先后循环是可以颠倒的！

但如果题目稍稍有点变化，就会体现在遍历顺序上。

如果问装满背包有几种方式的话？ 那么两个for循环的先后顺序就有很大区别了，而leetcode上的题目都是这种稍有变化的类型。

这个区别，我将在后面讲解具体leetcode题目中给大家介绍，因为这块如果不结合具题目，单纯的介绍原理估计很多同学会越看越懵！

别急，下一篇就是了！

最后，又可以出一道面试题了，就是纯完全背包，要求先用二维dp数组实现，然后再用一维dp数组实现，最后再问，两个for循环的先后是否可以颠倒？为什么？

这个简单的完全背包问题，估计就可以难住不少候选人了。

其他语言版本

Java：

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt();
        int bagWeight = scanner.nextInt();

        int[] weight = new int[N];
        int[] value = new int[N];
        for (int i = 0; i < N; i++) {
            weight[i] = scanner.nextInt();
            value[i] = scanner.nextInt();
        }

        int[] dp = new int[bagWeight + 1];

        for (int j = 0; j <= bagWeight; j++) { // 遍历背包容量
            for (int i = 0; i < weight.length; i++) { // 遍历物品
                if (j >= weight[i]) {
                    dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
                }
            }
        }

        System.out.println(dp[bagWeight]);
        scanner.close();
    }
}

Python：

def complete_knapsack(N, bag_weight, weight, value):
    dp = [0] * (bag_weight + 1)

    for j in range(bag_weight + 1):  # 遍历背包容量
        for i in range(len(weight)):  # 遍历物品
            if j >= weight[i]:
                dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

    return dp[bag_weight]

# 输入
N, bag_weight = map(int, input().split())
weight = []
value = []
for _ in range(N):
    w, v = map(int, input().split())
    weight.append(w)
    value.append(v)

# 输出结果
print(complete_knapsack(N, bag_weight, weight, value))

Go：

Javascript: