.
+}
+\seealso{
+Useful links:
+\itemize{
+ \item \url{https://data.lesslikely.com/concurve/}
+ \item \url{https://github.com/zadchow/concurve}
+ \item \url{https://lesslikely.com/}
+ \item Report bugs at \url{https://github.com/zadchow/concurve/issues}
+}
+
+}
+\author{
+\strong{Maintainer}: Zad R. Chow \email{zad@lesslikely.com} (\href{https://orcid.org/0000-0003-1545-8199}{ORCID})
+
+Authors:
+\itemize{
+ \item Andrew D. Vigotsky (\href{https://orcid.org/0000-0003-3166-0688}{ORCID})
+}
+
+}
+\keyword{internal}
diff --git a/man/curve_boot.Rd b/man/curve_boot.Rd
new file mode 100644
index 0000000..154012c
--- /dev/null
+++ b/man/curve_boot.Rd
@@ -0,0 +1,67 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/curve_boot.R
+\name{curve_boot}
+\alias{curve_boot}
+\title{Generate Consonance Functions via Bootstrapping}
+\usage{
+curve_boot(
+ data = data,
+ func = func,
+ method = "bca",
+ replicates = 2000,
+ steps = 1000,
+ table = TRUE
+)
+}
+\arguments{
+\item{data}{Dataset that is being used to create a consonance function.}
+
+\item{func}{Custom function that is used to create parameters of interest that
+will be bootstrapped.}
+
+\item{method}{The boostrap method that will be used to generate the functions.
+Methods include "bca" which is the default and "t".}
+
+\item{replicates}{Indicates how many bootstrap replicates are to be performed.
+The defaultis currently 20000 but more may be desirable, especially to make
+the functions more smooth.}
+
+\item{steps}{Indicates how many consonance intervals are to be calculated at
+various levels. For example, setting this to 100 will produce 100 consonance
+intervals from 0 to 100. Setting this to 10000 will produce more consonance
+levels. By default, it is set to 1000. Increasing the number substantially
+is not recommended as it will take longer to produce all the intervals and
+store them into a dataframe.}
+
+\item{table}{Indicates whether or not a table output with some relevant
+statistics should be generated. The default is TRUE and generates a table
+which is included in the list object.}
+}
+\value{
+A list with the dataframe of values in the first list and the table
+in the second if table = TRUE.
+}
+\description{
+Use the BCa bootstrap method and the t boostrap method from the bcaboot and boot packages
+to generate consonance distrbutions.
+}
+\examples{
+
+\donttest{
+data(diabetes, package = "bcaboot")
+Xy <- cbind(diabetes$x, diabetes$y)
+rfun <- function(Xy) {
+ y <- Xy[, 11]
+ X <- Xy[, 1:10]
+ return(summary(lm(y ~ X))$adj.r.squared)
+}
+
+x <- curve_boot(data = Xy, func = rfun, method = "bca", replicates = 200, steps = 1000)
+
+ggcurve(data = x[[1]])
+ggcurve(data = x[[3]])
+
+plot_compare(x[[1]], x[[3]])
+}
+
+}
diff --git a/man/curve_compare.Rd b/man/curve_compare.Rd
new file mode 100644
index 0000000..85b775e
--- /dev/null
+++ b/man/curve_compare.Rd
@@ -0,0 +1,47 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/curve_compare.R
+\name{curve_compare}
+\alias{curve_compare}
+\title{Compares two functions and produces an AUC score to show the amount of consonance.}
+\usage{
+curve_compare(data1, data2, type = "c", plot = TRUE, ...)
+}
+\arguments{
+\item{data1}{The first dataframe produced by one of the interval functions
+in which the intervals are stored.}
+
+\item{data2}{The second dataframe produced by one of the interval functions in
+which the intervals are stored.}
+
+\item{type}{Choose whether to plot a "consonance" function, a "surprisal" function or
+"likelihood". The default option is set to "c". The type must be set in quotes,
+for example curve_compare (type = "s") or curve_compare(type = "c"). Other options
+include "pd" for the consonance distribution function, and "cd" for the consonance
+density function, "l1" for relative likelihood, "l2" for log-likelihood, "l3"
+for likelihood and "d" for deviance function.}
+
+\item{plot}{by default it is set to TRUE and will use the plot_compare() function
+to plot the two functions.}
+
+\item{...}{Can be used to pass further arguments to plot_compare().}
+}
+\description{
+Compares the p-value/s-value, and likelihood functions and computes an AUC number.
+}
+\examples{
+\donttest{
+library(concurve)
+GroupA <- rnorm(50)
+GroupB <- rnorm(50)
+RandomData <- data.frame(GroupA, GroupB)
+intervalsdf <- curve_mean(GroupA, GroupB, data = RandomData)
+GroupA2 <- rnorm(50)
+GroupB2 <- rnorm(50)
+RandomData2 <- data.frame(GroupA2, GroupB2)
+model <- lm(GroupA2 ~ GroupB2, data = RandomData2)
+randomframe <- curve_gen(model, "GroupB2")
+(curve_compare(intervalsdf[[1]], randomframe[[1]]))
+(curve_compare(intervalsdf[[1]], randomframe[[1]], type = "s"))
+}
+
+}
diff --git a/man/curve_corr.Rd b/man/curve_corr.Rd
index 9a4fdfd..bbe100f 100644
--- a/man/curve_corr.Rd
+++ b/man/curve_corr.Rd
@@ -1,55 +1,47 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/curve_corr.R
\name{curve_corr}
\alias{curve_corr}
-
-\title{Computes consonance intervals for correlations
-}
-\description{
-Computes consonance intervals to produce P- and S-value functions for correlational analyses
-using the cor.test function in base R and places the interval limits for each interval level
-into a data frame along with the corresponding p-values and s-values.
-
-}
+\title{Computes Consonance Intervals for Correlations}
\usage{
-curve_corr(x, y, alternative, method, steps = 10000)
+curve_corr(x, y, alternative, method, steps = 10000, table = TRUE)
}
-
\arguments{
- \item{x}{
-A vector that contains the data for one of the variables that will be analyzed for correlational analysis.
-}
- \item{y}{
-A vector that contains the data for one of the variables that will be analyzed for correlational analysis.
-}
- \item{alternative}{
-Indicates the alternative hypothesis and must be one of "two.sided", "greater" or "less". You can specify just the initial letter. "greater" corresponds to positive association, "less" to negative association.
-}
- \item{method}{
-A character string indicating which correlation coefficient is to be used for the test. One of "pearson", "kendall", or "spearman", can be abbreviated.
-}
- \item{steps}{
-Indicates how many consonance intervals are to be calculated at various levels. For example, setting
-this to 100 will produce 100 consonance intervals from 0 to 100. Setting this to 10000 will produce more consonance levels. By default, it is set to 1000. Increasing the number substantially is not recommended as it will take longer to produce all the intervals and store them into a dataframe.
-}
-}
+\item{x}{A vector that contains the data for one of the variables that will
+be analyzed for correlational analysis.}
-\references{
-Poole C. Beyond the confidence interval. Am J Public Health. 1987;77(2):195-199.
+\item{y}{A vector that contains the data for one of the variables that will
+be analyzed for correlational analysis.}
-Sullivan KM, Foster DA. Use of the confidence interval function. Epidemiology. 1990;1(1):39-42.
+\item{alternative}{Indicates the alternative hypothesis and must be one of "two.sided",
+"greater" or "less". You can specify just the initial letter. "greater" corresponds to
+positive association, "less" to negative association.}
-Rothman KJ, Greenland S, Lash TL, Others. Modern epidemiology. 2008.
-}
+\item{method}{A character string indicating which correlation coefficient is
+to be used for the test. One of "pearson", "kendall", or "spearman",
+can be abbreviated.}
+
+\item{steps}{Indicates how many consonance intervals are to be calculated at
+various levels. For example, setting this to 100 will produce 100 consonance
+intervals from 0 to 100. Setting this to 10000 will produce more consonance
+levels. By default, it is set to 1000. Increasing the number substantially
+is not recommended as it will take longer to produce all the intervals and
+store them into a dataframe.}
+\item{table}{Indicates whether or not a table output with some relevant
+statistics should be generated. The default is TRUE and generates a table
+which is included in the list object.}
+}
+\description{
+Computes consonance intervals to produce P- and S-value functions for
+correlational analysesusing the cor.test function in base R and places the
+interval limits for each interval levelinto a data frame along with the
+corresponding p-values and s-values.
+}
\examples{
GroupA <- rnorm(50)
GroupB <- rnorm(50)
-
-joe <- curve_corr(x = GroupA, y = GroupB,
- alternative = "two.sided", method = "pearson")
-
-tibble::tibble(joe)
-
+joe <- curve_corr(x = GroupA, y = GroupB, alternative = "two.sided", method = "pearson")
+tibble::tibble(joe[[1]])
}
-
-
diff --git a/man/curve_gen.Rd b/man/curve_gen.Rd
index 07cca57..16be64d 100644
--- a/man/curve_gen.Rd
+++ b/man/curve_gen.Rd
@@ -1,62 +1,57 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/curve_gen.R
\name{curve_gen}
\alias{curve_gen}
-
-\title{Computes consonance intervals for linear models
-
-}
-\description{
-Computes thousands of consonance (confidence) intervals for the chosen parameter in the
-selected model(ANOVA, ANCOVA, regression, logistic regression) and places the interval limits
-for each interval level into a data frame along with the corresponding p-values and s-values.
-}
+\title{General Consonance Functions Using Profile Likelihood, Wald,
+or the bootstrap method for linear models.}
\usage{
-curve_gen(model, var, method = "default", replicates = 1000, steps = 10000)
+curve_gen(model, var, method = "wald", steps = 1000, table = TRUE)
}
-
\arguments{
- \item{model}{
-The statistical model of interest(ANOVA, regression, logistic regression) is to be indicated here.
-}
- \item{var}{
-The variable of interest from the model (coefficients, intercept) for which the intervals are to be produced.
-}
- \item{method}{
-Chooses the method to be used to calculate the consonance intervals. There are currently four
-methods: "default", "wald", "lm", and "boot". The "default" method uses the profile likelihood method to
-compute intervals and can be used for models created by the 'lm' function. The "wald" method is typically
-what most people are familiar with when computing intervals based on the calculated standard error.
-The "lm" method allows this function to be used for specific scenarios like logistic regression and
-the 'glm' function. The "boot" method allows for bootstrapping at certain levels.
-}
- \item{replicates}{
-Indicates how many bootstrap replicates are to be performed if bootstrapping is enabled as a method.
-}
- \item{steps}{
-Indicates how many consonance intervals are to be calculated at various levels. For example, setting
-this to 100 will produce 100 compatibility intervals from 0 to 100. Setting this to 10000 will produce more consonance levels. By default, it is set to 1000. Increasing the number substantially is not recommended as it will take longer to produce all the intervals and store them into a dataframe.
-}
+\item{model}{The statistical model of interest
+(ANOVA, regression, logistic regression) is to be indicated here.}
+
+\item{var}{The variable of interest from the model (coefficients, intercept)
+for which the intervals are to be produced.}
+
+\item{method}{Chooses the method to be used to calculate the
+consonance intervals. There are currently four methods:
+"default", "wald", "lm", and "boot". The "default" method uses the profile
+likelihood method to compute intervals and can be used for models created by
+the 'lm' function. The "wald" method is typicallywhat most people are
+familiar with when computing intervals based on the calculated standard error.
+The "lm" method allows this function to be used for specific scenarios like
+logistic regression and the 'glm' function. The "boot" method allows for
+bootstrapping at certain levels.}
+
+\item{steps}{Indicates how many consonance intervals are to be calculated at
+various levels. For example, setting this to 100 will produce 100 consonance
+intervals from 0 to 100. Setting this to 10000 will produce more consonance
+levels. By default, it is set to 1000. Increasing the number substantially
+is not recommended as it will take longer to produce all the intervals and
+store them into a dataframe.}
+
+\item{table}{Indicates whether or not a table output with some relevant
+statistics should be generated. The default is TRUE and generates a table
+which is included in the list object.}
}
-
-\references{
-Poole C. Beyond the confidence interval. Am J Public Health. 1987;77(2):195-199.
-
-Sullivan KM, Foster DA. Use of the confidence interval function. Epidemiology. 1990;1(1):39-42.
-
-Rothman KJ, Greenland S, Lash TL, Others. Modern epidemiology. 2008.
+\description{
+Computes thousands of consonance (confidence) intervals for
+the chosen parameter in the selected model
+(ANOVA, ANCOVA, regression, logistic regression) and places
+the interval limits for each interval level into a data frame along
+with the corresponding p-values and s-values.
}
-
\examples{
+\donttest{
# Simulate random data
-
GroupA <- rnorm(50)
GroupB <- rnorm(50)
-
RandomData <- data.frame(GroupA, GroupB)
-
-rob <- glm(GroupA ~ GroupB, data = RandomData)
-bob <- curve_gen(rob, "GroupB", method = "lm")
-
-tibble::tibble(bob)
+rob <- lm(GroupA ~ GroupB, data = RandomData)
+bob <- curve_gen(rob, "GroupB")
+tibble::tibble(bob[[1]])
+}
}
diff --git a/man/curve_lik.Rd b/man/curve_lik.Rd
new file mode 100644
index 0000000..2c37e48
--- /dev/null
+++ b/man/curve_lik.Rd
@@ -0,0 +1,29 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/curve_lik.R
+\name{curve_lik}
+\alias{curve_lik}
+\title{Compute the Profile Likelihood Functions}
+\usage{
+curve_lik(likobject, data, table = TRUE)
+}
+\arguments{
+\item{likobject}{An object from the ProfileLikelihood package}
+
+\item{data}{The dataframe that was used to create the likelihood
+object in the ProfileLikelihood package.}
+
+\item{table}{Indicates whether or not a table output with some relevant
+statistics should be generated. The default is TRUE and generates a table
+which is included in the list object.}
+}
+\description{
+Compute the Profile Likelihood Functions
+}
+\examples{
+
+library(ProfileLikelihood)
+data(dataglm)
+xx <- profilelike.glm(y ~ x1 + x2, dataglm, profile.theta = "group", binomial("logit"))
+lik <- curve_lik(xx, dataglm)
+tibble::tibble(lik[[1]])
+}
diff --git a/man/curve_mean.Rd b/man/curve_mean.Rd
index 0e9b00b..a51a5da 100644
--- a/man/curve_mean.Rd
+++ b/man/curve_mean.Rd
@@ -1,66 +1,62 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/curve_mean.R
\name{curve_mean}
\alias{curve_mean}
-
-\title{Computes consonance intervals for mean differences
-}
-\description{
-Computes thousands of consonance (confidence) intervals for the chosen parameter in a statistical test
-that compares means and places the interval limits for each interval level into a data frame along with the corresponding p-values and s-values.
-}
+\title{Mean Interval Consonance Function}
\usage{
-curve_mean(x, y, data, paired = F, method = "default",
-replicates = 1000, steps = 10000)
+curve_mean(
+ x,
+ y,
+ data,
+ paired = F,
+ method = "default",
+ replicates = 1000,
+ steps = 10000,
+ table = TRUE
+)
}
-
\arguments{
- \item{x}{
-Variable that contains the data for the first group being compared.
-}
- \item{y}{
-Variable that contains the data for the second group being compared.
-}
- \item{data}{
-Data frame from which the variables are being extracted from.
-}
- \item{paired}{
-Indicates whether the statistical test is a paired difference test. By default, it is set to "F",
-which means the function will be an unpaired statistical test comparing two independent groups.
-Inserting "paired" will change the test to a paired difference test.
-}
- \item{method}{
-By default this is turned off (set to "default"), but allows for bootstrapping if "boot" is inserted
-into the function call.
-}
- \item{replicates}{
-Indicates how many bootstrap replicates are to be performed if bootstrapping is enabled as a method.
-}
- \item{steps}{
-Indicates how many consonance intervals are to be calculated at various levels. For example, setting
-this to 100 will produce 100 consonance intervals from 0 to 100. Setting this to 10000 will produce more
-consonance levels. By default, it is set to 1000. Increasing the number substantially is not recommended
-as it will take longer to produce all the intervals and store them into a dataframe.
-}
-}
+\item{x}{Variable that contains the data for the first group being compared.}
-\references{
-Poole C. Beyond the confidence interval. Am J Public Health. 1987;77(2):195-199.
+\item{y}{Variable that contains the data for the second group being compared.}
-Sullivan KM, Foster DA. Use of the confidence interval function. Epidemiology. 1990;1(1):39-42.
+\item{data}{Data frame from which the variables are being extracted from.}
-Rothman KJ, Greenland S, Lash TL, Others. Modern epidemiology. 2008.
-}
+\item{paired}{Indicates whether the statistical test is a paired difference test.
+By default, it is set to "F",which means the function will be an unpaired
+statistical test comparing two independent groups.Inserting "paired" will
+change the test to a paired difference test.}
+
+\item{method}{By default this is turned off (set to "default"), but
+allows for bootstrapping if "boot" is insertedinto the function call.}
+
+\item{replicates}{Indicates how many bootstrap replicates are to be performed.
+The defaultis currently 20000 but more may be desirable, especially to make
+the functions more smooth.}
+\item{steps}{Indicates how many consonance intervals are to be calculated at
+various levels. For example, setting this to 100 will produce 100 consonance
+intervals from 0 to 100. Setting this to 10000 will produce more consonance
+levels. By default, it is set to 1000. Increasing the number substantially
+is not recommended as it will take longer to produce all the intervals and
+store them into a dataframe.}
+
+\item{table}{Indicates whether or not a table output with some relevant
+statistics should be generated. The default is TRUE and generates a table
+which is included in the list object.}
+}
+\description{
+Computes thousands of consonance (confidence) intervals for the chosen
+parameter in a statistical test that compares means and places the interval
+limits for each interval level into a data frame along with the corresponding
+p-values and s-values.
+}
\examples{
# Simulate random data
-
GroupA <- runif(100, min = 0, max = 100)
GroupB <- runif(100, min = 0, max = 100)
-
RandomData <- data.frame(GroupA, GroupB)
-
bob <- curve_mean(GroupA, GroupB, RandomData)
-
-tibble::tibble(bob)
-
+tibble::tibble(bob[[1]])
}
diff --git a/man/curve_meta.Rd b/man/curve_meta.Rd
index 0c42f81..f3a6eed 100644
--- a/man/curve_meta.Rd
+++ b/man/curve_meta.Rd
@@ -1,48 +1,41 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/curve_meta.R
\name{curve_meta}
\alias{curve_meta}
-
-\title{Computes consonance intervals for meta-analysis data
-}
-\description{
-Computes thousands of consonance (confidence) intervals for the chosen parameter in the
-meta-analysis done by the metafor package and places the interval limits for each interval level
-into a data frame along with the corresponding p-values and s-values.
-}
+\title{Meta-analytic Consonance Function}
\usage{
-curve_meta(x, measure = "default", steps = 10000)
+curve_meta(x, measure = "default", steps = 10000, table = TRUE)
}
-
\arguments{
- \item{x}{
-Object where the meta-analysis parameters are stored, typically a list produced by 'metafor'
-}
- \item{measure}{
-Indicates whether the object has a log transformation or is normal/default. The default setting is "default.
-If the measure is set to "ratio", it will take logarithmically transformed values and convert them back to normal values in the dataframe. This is typically a setting used for binary outcomes such as risk ratios, hazard ratios, and odds ratios.
-}
- \item{steps}{
-Indicates how many consonance intervals are to be calculated at various levels. For example, setting
-this to 100 will produce 100 consonance intervals from 0 to 100. Setting this to 10000 will produce more
-consonance levels. By default, it is set to 1000. Increasing the number substantially is not recommended
-as it will take longer to produce all the intervals and store them into a dataframe.
-}
+\item{x}{Object where the meta-analysis parameters are stored, typically a
+list produced by 'metafor'}
+
+\item{measure}{Indicates whether the object has a log transformation or is normal/default.
+The default setting is "default. If the measure is set to "ratio", it will take
+logarithmically transformed values and convert them back to normal values in the dataframe.
+This is typically a setting used for binary outcomes such as risk ratios,
+hazard ratios, and odds ratios.}
+
+\item{steps}{Indicates how many consonance intervals are to be calculated at
+various levels. For example, setting this to 100 will produce 100 consonance
+intervals from 0 to 100. Setting this to 10000 will produce more consonance
+levels. By default, it is set to 1000. Increasing the number substantially
+is not recommended as it will take longer to produce all the intervals and
+store them into a dataframe.}
+
+\item{table}{Indicates whether or not a table output with some relevant
+statistics should be generated. The default is TRUE and generates a table
+which is included in the list object.}
}
-
-\references{
-Viechtbauer W. Conducting meta-analyses in R with the metafor package. J Stat Softw. 2010;36(3).
-https://www.jstatsoft.org/article/view/v036i03/v36i03.pdf.
-
-Poole C. Beyond the confidence interval. Am J Public Health. 1987;77(2):195-199.
-
-Sullivan KM, Foster DA. Use of the confidence interval function. Epidemiology. 1990;1(1):39-42.
-
-Rothman KJ, Greenland S, Lash TL, Others. Modern epidemiology. 2008.
+\description{
+Computes thousands of consonance (confidence) intervals for the chosen
+parameter in the meta-analysis done by the metafor package and places the
+interval limits for each interval level into a data frame along with the
+corresponding p-values and s-values.
}
-
\examples{
# Simulate random data for two groups in two studies
-
GroupAData <- runif(20, min = 0, max = 100)
GroupAMean <- round(mean(GroupAData), digits = 2)
GroupASD <- round(sd(GroupAData), digits = 2)
@@ -79,17 +72,21 @@ metadf <- data.frame(
library(metafor)
dat <- escalc(
- measure = "SMD", m1i = MeanTreatment, sd1i = SDTreatment, n1i = NTreatment,
- m2i = MeanControl, sd2i = SDControl, n2i = NControl, data = metadf
+ measure = "SMD", m1i = MeanTreatment, sd1i = SDTreatment,
+ n1i = NTreatment, m2i = MeanControl, sd2i = SDControl,
+ n2i = NControl, data = metadf
)
# Pool the data using a particular method. Here "FE" is the fixed-effects model
-res <- rma(yi, vi, data = dat, slab = paste(StudyName, sep = ", "), method = "FE", digits = 2)
+res <- rma(yi, vi,
+ data = dat, slab = paste(StudyName, sep = ", "),
+ method = "FE", digits = 2
+)
# Calculate the intervals using the metainterval function
metaf <- curve_meta(res)
-tibble::tibble(metaf)
+tibble::tibble(metaf[[1]])
}
diff --git a/man/curve_rev.Rd b/man/curve_rev.Rd
index a366bab..6ba3cc0 100644
--- a/man/curve_rev.Rd
+++ b/man/curve_rev.Rd
@@ -1,59 +1,55 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/curve_rev.R
\name{curve_rev}
\alias{curve_rev}
-
-\title{
-Reverse engineer consonance and surprisal functions from confidence limits and point estimates
-}
-\description{
-Using the confidence limits and point estimates from a dataset, one can use these estimates to
-compute thousands of consonance intervals and graph the intervals to form a consonance and
-surprisal function.
-}
+\title{Reverse Engineer Consonance / Likelihood Functions Using the Point
+Estimate and Confidence Limits}
\usage{
-curve_rev(point, LL, UL, measure = "default", steps = 10000)
+curve_rev(
+ point,
+ LL,
+ UL,
+ type = "c",
+ measure = "default",
+ steps = 10000,
+ table = TRUE
+)
}
-
\arguments{
- \item{point}{
-The point estimate from an analysis. Ex: 1.20
-}
- \item{LL}{
-The lower confidence limit from an analysis Ex: 1.0
-}
- \item{UL}{
-The upper confidence limit from an analysis Ex: 1.4
-}
- \item{measure}{
-The type of data being used. If they involve mean differences,
-then the "default" option should be used, which is also the default setting.
-If the data are ratios, then the "ratio" option should be used.
-}
- \item{steps}{
-Indicates how many consonance intervals are to be calculated at various levels. For example, setting
-this to 100 will produce 100 consonance intervals from 0 to 100. Setting this to 10000 will produce more
-consonance levels. By default, it is set to 1000. Increasing the number substantially is not recommended
-as it will take longer to produce all the intervals and store them into a dataframe.
-}
+\item{point}{The point estimate from an analysis. Ex: 1.20}
-}
+\item{LL}{The lower confidence limit from an analysis Ex: 1.0}
-\references{
-Poole C. Beyond the confidence interval. Am J Public Health. 1987;77(2):195-199.
+\item{UL}{The upper confidence limit from an analysis Ex: 1.4}
-Sullivan KM, Foster DA. Use of the confidence interval function. Epidemiology. 1990;1(1):39-42.
+\item{type}{Indicates whether the produced result should be a consonance
+function or a likelihood function. The default is "c" for consonance and
+likelihood can be set via "l".}
-Rothman KJ, Greenland S, Lash TL, Others. Modern epidemiology. 2008.
-}
+\item{measure}{The type of data being used. If they involve mean differences,}
+
+\item{steps}{Indicates how many consonance intervals are to be calculated at
+various levels. For example, setting this to 100 will produce 100 consonance
+intervals from 0 to 100. Setting this to 10000 will produce more consonance
+levels. By default, it is set to 1000. Increasing the number substantially
+is not recommended as it will take longer to produce all the intervals and
+store them into a dataframe.}
+\item{table}{Indicates whether or not a table output with some relevant
+statistics should be generated. The default is TRUE and generates a table
+which is included in the list object.}
+}
+\description{
+Using the confidence limits and point estimates from a dataset, one can use
+these estimates to compute thousands of consonance intervals and graph the
+intervals to form a consonance and surprisal function.
+}
\examples{
# From a real published study. Point estimate of the result was hazard ratio of 1.61 and
# lower bound of the interval is 0.997 while upper bound of the interval is 2.59.
-
+#
df <- curve_rev(point = 1.61, LL = 0.997, UL = 2.59, measure = "ratio")
-tibble::tibble(df)
-
+tibble::tibble(df[[1]])
}
-
-
diff --git a/man/curve_surv.Rd b/man/curve_surv.Rd
index fa88cbd..2f91d5b 100644
--- a/man/curve_surv.Rd
+++ b/man/curve_surv.Rd
@@ -1,36 +1,32 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/curve_surv.R
\name{curve_surv}
\alias{curve_surv}
-%- Also NEED an '\alias' for EACH other topic documented here.
-\title{Produce Consonance Intervals for Survival Data
-}
-\description{
-Computes thousands of consonance (confidence) intervals for the chosen parameter in the
-Cox model computed by the 'survival' package and places the interval limits for each interval level
-into a data frame along with the corresponding p-value and s-value.
-}
+\title{Produce Consonance Intervals for Survival Data}
\usage{
-curve_surv(data, x, steps = 10000)
+curve_surv(data, x, steps = 10000, table = TRUE)
}
-%- maybe also 'usage' for other objects documented here.
\arguments{
- \item{data}{
-Object where the Cox model is stored, typically a list produced by the 'survival' package.
-}
- \item{x}{
-Predictor of interest within the survival model for which the consonance intervals should be computed.
-}
- \item{steps}{
-Indicates how many consonance intervals are to be calculated at various levels. For example, setting
-this to 100 will produce 100 consonance intervals from 0 to 100. Setting this to 10000 will produce more
-consonance levels. By default, it is set to 1000. Increasing the number substantially is not recommended
-as it will take longer to produce all the intervals and store them into a dataframe.
-}
-}
+\item{data}{Object where the Cox model is stored, typically a list produced by the
+'survival' package.}
-\references{
-Poole C. Beyond the confidence interval. Am J Public Health. 1987;77(2):195-199.
+\item{x}{Predictor of interest within the survival model for which the
+consonance intervals should be computed.}
-Sullivan KM, Foster DA. Use of the confidence interval function. Epidemiology. 1990;1(1):39-42.
+\item{steps}{Indicates how many consonance intervals are to be calculated at
+various levels. For example, setting this to 100 will produce 100 consonance
+intervals from 0 to 100. Setting this to 10000 will produce more consonance
+levels. By default, it is set to 1000. Increasing the number substantially
+is not recommended as it will take longer to produce all the intervals and
+store them into a dataframe.}
-Rothman KJ, Greenland S, Lash TL, Others. Modern epidemiology. 2008.
+\item{table}{Indicates whether or not a table output with some relevant
+statistics should be generated. The default is TRUE and generates a table
+which is included in the list object.}
+}
+\description{
+Computes thousands of consonance (confidence) intervals for the chosen
+parameter in the Cox model computed by the 'survival' package and places
+the interval limits for each interval level into a data frame along
+with the corresponding p-value and s-value.
}
diff --git a/man/curve_table.Rd b/man/curve_table.Rd
new file mode 100644
index 0000000..0d0014a
--- /dev/null
+++ b/man/curve_table.Rd
@@ -0,0 +1,41 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/curve_table.R
+\name{curve_table}
+\alias{curve_table}
+\title{Produce Tables For concurve Functions}
+\usage{
+curve_table(data, levels, type = "c", format = "data.frame")
+}
+\arguments{
+\item{data}{Dataframe from a concurve function to produce a table for}
+
+\item{levels}{Levels of the consonance intervals or likelihood intervals that should be
+included in the table.}
+
+\item{type}{Indicates whether the table is for a consonance function or likelihood function.
+The default is set to "c" for consonance and can be switched to "l" for likelihood.}
+
+\item{format}{The format of the tables. The options include "data.frame" which is the
+default, "tibble", "docx" (which creates a table for a word document), "pptx" (which
+creates a table for powerpoint), "latex", (which creates a table for a TeX document), and
+"image", which produces an image of the table.}
+}
+\description{
+Produces publication-ready tables with relevant statistics of interest
+for functions produced from the concurve package.
+}
+\examples{
+
+library(concurve)
+
+GroupA <- rnorm(500)
+GroupB <- rnorm(500)
+
+RandomData <- data.frame(GroupA, GroupB)
+
+intervalsdf <- curve_mean(GroupA, GroupB, data = RandomData, method = "default")
+
+(z <- curve_table(intervalsdf[[1]], format = "data.frame"))
+(z <- curve_table(intervalsdf[[1]], format = "tibble"))
+(z <- curve_table(intervalsdf[[1]], format = "latex"))
+}
diff --git a/man/defunct.Rd b/man/defunct.Rd
index 016d3e2..1febda9 100644
--- a/man/defunct.Rd
+++ b/man/defunct.Rd
@@ -9,6 +9,8 @@
\alias{survintervals}
\alias{likintervals}
\alias{rev_eng}
+\alias{ggconcurve}
+\alias{plot_concurve}
\title{Deprecated functions in \pkg{concurve}.}
\usage{
plotpint(...)
@@ -26,18 +28,34 @@ corrintervals(...)
survintervals(...)
rev_eng(...)
+
+ggconcurve(...)
+
+plot_concurve(...)
+
}
+
\description{
The functions listed below are deprecated. Please use the listed alternatives.}
\section{\code{plotpint}}{
-For \code{plotpint}, use \code{\link{ggconcurve}} or \code{\link{plot_concurve}}.
+For \code{plotpint}, use \code{\link{ggcurve}}.
}
\section{\code{plotsint}}{
-For \code{plotsint}, use \code{\link{ggconcurve}} or \code{\link{plot_concurve}}.
+For \code{plotsint}, use \code{\link{ggcurve}}.
+}
+
+\section{\code{plot_concurve}}{
+
+For \code{plot_concurve}, use \code{\link{ggcurve}}.
+}
+
+\section{\code{ggconcurve}}{
+
+For \code{ggconcurve}, use \code{\link{ggcurve}}.
}
\section{\code{meanintervals}}{
diff --git a/man/figures/.DS_Store b/man/figures/.DS_Store
index 08621ff..27902fb 100644
Binary files a/man/figures/.DS_Store and b/man/figures/.DS_Store differ
diff --git a/man/ggconcurve.Rd b/man/ggconcurve.Rd
deleted file mode 100644
index e6f5ce1..0000000
--- a/man/ggconcurve.Rd
+++ /dev/null
@@ -1,81 +0,0 @@
-\name{ggconcurve}
-\alias{ggconcurve}
-
-\title{
-Plots the P-Value (Consonance) and S-value (Surprisal) Function via ggplot2
-}
-\description{
-Takes the dataframe produced by the interval functions and plots the p-values/s-values, consonance (confidence)
-levels, and the interval estimates to produce a p-value/s-value function using ggplot2 graphics.
-}
-\usage{
-ggconcurve(type, data, measure, nullvalue, position,
- title, subtitle, xaxis, yaxis, color, fill)
-}
-
-\arguments{
- \item{type}{
-Choose whether to plot a "consonance" function or a "surprisal" function. The default option is set to "consonance". The type must be set in quotes, for example ggconcurve(type = "surprisal") or ggconcurve(type = "consonance").
-}
- \item{data}{
-The dataframe produced by one of the interval functions in which the intervals are stored.
-}
- \item{measure}{
-Indicates whether the object has a log transformation or is normal/default. The default setting is "default". If the measure is set to "ratio", it will take logarithmically transformed values and convert them back to normal values in the dataframe. This is typically a setting used for binary outcomes and their measures such as risk ratios, hazard ratios, and odds ratios.
-}
- \item{nullvalue}{
-Indicates whether the null value for the measure should be plotted. By default, it is set to "absent", meaning it will not be plotted as a vertical line. Changing this to "present", will plot a vertical line at 0 when the measure is set to "default" and a vertical line at 1 when the measure is set to "ratio". For example, ggconcurve(type = "consonance", data = df, measure = "ratio", nullvalue = "present"). This feature is not yet available for surprisal functions.
-}
-
- \item{position}{
-Determines the orientation of the P-value (consonance) function By default, it is set to "pyramid", meaning the p-value function will stand right side up, like a pyramid. However, it can also be inverted via the option "inverted". This will also change the sequence of the y-axes to match the orientation. This can be set as such, ggconcurve(type = "consonance", data = df, position = "inverted")
-}
-
- \item{title}{
-A custom title for the graph. By default, it is set to "Consonance Function". In order to set a title, it must be in quotes. For example, ggconcurve(type = "consonance", data = x, title = "Custom Title").
-}
- \item{subtitle}{
-A custom subtitle for the graph. By default, it is set to "The function contains consonance/confidence intervals at every level and the P-values." In order to set a subtitle, it must be in quotes. For example, ggconcurve(type = "consonance", data = x, subtitle = "Custom Subtitle").
-}
-
- \item{xaxis}{
-A custom x-axis title for the graph. By default, it is set to "Range of Values. In order to set a x-axis title, it must be in quotes. For example, ggconcurve(type = "consonance", data = x, xaxis = "Hazard Ratio").
-}
- \item{yaxis}{
-A custom y-axis title for the graph. By default, it is set to "Consonance Level". In order to set a y-axis title, it must be in quotes. For example, ggconcurve(type = "consonance", data = x, yxis = "Confidence Level").
-}
- \item{color}{
-Item that allows the user to choose the color of the points and the ribbons in the graph. By default, it is set to color = "#555555". The inputs must be in quotes. For example, ggconcurve(type = "consonance", data = x, color = "#333333").
-}
- \item{fill}{
-Item that allows the user to choose the color of the ribbons in the graph. By default, it is set to color = "#239a98". The inputs must be in quotes. For example, ggconcurve(type = "consonance", data = x, fill = "#333333").
-}
-}
-
-\value{
-Plot with intervals at every consonance level graphed with their corresponding p-values and compatibility levels.
-}
-\references{
-Poole C. Beyond the confidence interval. Am J Public Health. 1987;77(2):195-199.
-
-Sullivan KM, Foster DA. Use of the confidence interval function. Epidemiology. 1990;1(1):39-42.
-
-Rothman KJ, Greenland S, Lash TL, Others. Modern epidemiology. 2008.
-}
-
-\examples{
-# Simulate random data
-
-GroupA <- rnorm(50)
-GroupB <- rnorm(50)
-
-RandomData <- data.frame(GroupA, GroupB)
-RandomModel <- lm(GroupA ~ GroupB, data = RandomData)
-
-intervalsdf <- curve_gen(RandomModel, "GroupB")
-
-ggconcurve(type = "consonance", data = intervalsdf, nullvalue = "present")
-
-ggconcurve(type = "surprisal", data = intervalsdf)
-
-}
diff --git a/man/ggcurve.Rd b/man/ggcurve.Rd
new file mode 100644
index 0000000..a6c481f
--- /dev/null
+++ b/man/ggcurve.Rd
@@ -0,0 +1,114 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/ggcurve.R
+\name{ggcurve}
+\alias{ggcurve}
+\title{Plots the P-Value (Consonance), S-value (Surprisal),
+and Likelihood Function via ggplot2}
+\usage{
+ggcurve(
+ data,
+ type = "c",
+ measure = "default",
+ levels = 0.95,
+ nullvalue = FALSE,
+ position = "pyramid",
+ title = "Interval Function",
+ subtitle = "The function displays intervals at every level.",
+ xaxis = expression(Theta ~ "Range of Values"),
+ yaxis = "P-value",
+ color = "#000000",
+ fill = "#239a98"
+)
+}
+\arguments{
+\item{data}{The dataframe produced by one of the interval functions
+in which the intervals are stored.}
+
+\item{type}{Choose whether to plot a "consonance" function, a
+"surprisal" function or "likelihood". The default option is set to "c".
+The type must be set in quotes, for example ggcurve (type = "s") or
+ggcurve(type = "c"). Other options include "pd" for the consonance
+distribution function, and "cd" for the consonance density function,
+"l1" for relative likelihood, "l2" for log-likelihood, "l3" for likelihood
+and "d" for deviance function.}
+
+\item{measure}{Indicates whether the object has a log transformation
+or is normal/default. The default setting is "default". If the measure
+is set to "ratio", it will take logarithmically transformed values and
+convert them back to normal values in the dataframe. This is typically a
+setting used for binary outcomes and their measures such as risk ratios,
+hazard ratios, and odds ratios.}
+
+\item{levels}{Indicates which interval levels should be plotted on the function.
+By default it is set to 0.95 to plot the 95\% interval on the consonance function,
+but more levels can be plotted by using the c() function for example,
+levels = c(0.50, 0.75, 0.95).}
+
+\item{nullvalue}{Indicates whether the null value for the measure
+should be plotted. By default, it is set to FALSE, meaning it will not be
+plotted as a vertical line. Changing this to TRUE, will plot a vertical
+line at 0 when the measure is set to " default" and a vertical line at
+1 when the measure is set to "ratio". For example,
+ggcurve(type = "c", data = df, measure = "ratio", nullvalue = "present").
+This feature is not yet available for surprisal functions.}
+
+\item{position}{Determines the orientation of the P-value (consonance) function.
+By default, it is set to "pyramid", meaning the p-value function will
+stand right side up, like a pyramid. However, it can also be inverted
+via the option "inverted". This will also change the sequence of the
+y-axes to match the orientation.This can be set as such,
+ggcurve(type = "c", data = df, position = "inverted").}
+
+\item{title}{A custom title for the graph. By default, it is
+set to "Consonance Function". In order to set a title, it must
+be in quotes. For example, ggcurve(type = "c",
+data = x, title = "Custom Title").}
+
+\item{subtitle}{A custom subtitle for the graph. By default, it is set
+to "The function contains consonance/confidence intervals at every level
+and the P-values." In order to set a subtitle, it must be in quotes.
+For example, ggcurve(type = "c", data = x, subtitle = "Custom Subtitle").}
+
+\item{xaxis}{A custom x-axis title for the graph. By default,
+it is set to "Range of Values.
+In order to set a x-axis title, it must be in quotes. For example,
+ggcurve(type = "c", data = x, xaxis = "Hazard Ratio").}
+
+\item{yaxis}{A custom y-axis title for the graph. By default,
+it is set to "Consonance Level".
+In order to set a y-axis title, it must be in quotes. For example,
+ggcurve(type = "c", data = x, yxis = "Confidence Level").}
+
+\item{color}{Item that allows the user to choose the color of the points
+and the ribbons in the graph. By default, it is set to color = "#555555".
+The inputs must be in quotes.
+For example, ggcurve(type = "c", data = x, color = "#333333").}
+
+\item{fill}{Item that allows the user to choose the color of the ribbons in the graph.
+By default, it is set to fill = "#239a98". The inputs must be in quotes. For example,
+ggcurve(type = "c", data = x, fill = "#333333").}
+}
+\value{
+Plot with intervals at every consonance level graphed with their corresponding
+p-values and compatibility levels.
+}
+\description{
+Takes the dataframe produced by the interval functions and
+plots the p-values/s-values, consonance (confidence) levels, and
+the interval estimates to produce a p-value/s-value function
+using ggplot2 graphics.
+}
+\examples{
+
+# Simulate random data
+
+library(concurve)
+
+GroupA <- rnorm(500)
+GroupB <- rnorm(500)
+
+RandomData <- data.frame(GroupA, GroupB)
+
+intervalsdf <- curve_mean(GroupA, GroupB, data = RandomData, method = "default")
+(function1 <- ggcurve(type = "c", intervalsdf[[1]]))
+}
diff --git a/man/plot_compare.Rd b/man/plot_compare.Rd
new file mode 100644
index 0000000..b6ee81c
--- /dev/null
+++ b/man/plot_compare.Rd
@@ -0,0 +1,117 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/plot_compare.R
+\name{plot_compare}
+\alias{plot_compare}
+\title{Compares the P-Value (Consonance), S-value (Surprisal), and Likelihood Function via ggplot2}
+\usage{
+plot_compare(
+ data1,
+ data2,
+ type = "c",
+ measure = "default",
+ nullvalue = FALSE,
+ position = "pyramid",
+ title = "Interval Functions",
+ subtitle = "The function displays intervals at every level.",
+ xaxis = expression(Theta ~ "Range of Values"),
+ yaxis = "P-value",
+ color = "#000000",
+ fill1 = "#239a98",
+ fill2 = "#d46c5b"
+)
+}
+\arguments{
+\item{data1}{The first dataframe produced by one of the interval functions in which the
+intervals are stored.}
+
+\item{data2}{The second dataframe produced by one of the interval functions in which the
+intervals are stored.}
+
+\item{type}{Choose whether to plot a "consonance" function, a
+"surprisal" function or "likelihood". The default option is set to "c".
+The type must be set in quotes, for example plot_compare(type = "s") or
+plot_compare(type = "c"). Other options include "pd" for the consonance
+distribution function, and "cd" for the consonance density function,
+"l1" for relative likelihood, "l2" for log-likelihood, "l3" for likelihood
+and "d" for deviance function.}
+
+\item{measure}{Indicates whether the object has a log transformation
+or is normal/default. The default setting is "default". If the measure
+is set to "ratio", it will take logarithmically transformed values and
+convert them back to normal values in the dataframe. This is typically a
+setting used for binary outcomes and their measures such as risk ratios,
+hazard ratios, and odds ratios.}
+
+\item{nullvalue}{Indicates whether the null value for the measure
+should be plotted. By default, it is set to FALSE, meaning it will not be
+plotted as a vertical line. Changing this to TRUE, will plot a vertical
+line at 0 when the measure is set to " default" and a vertical line at
+1 when the measure is set to "ratio". For example,
+plot_compare(type = "c", data = df, measure = "ratio", nullvalue = "present").
+This feature is not yet available for surprisal functions.}
+
+\item{position}{Determines the orientation of the P-value (consonance) function.
+By default, it is set to "pyramid", meaning the p-value function will
+stand right side up, like a pyramid. However, it can also be inverted
+via the option "inverted". This will also change the sequence of the
+y-axes to match the orientation.This can be set as such,
+plot_compare(type = "c", data = df, position = "inverted").}
+
+\item{title}{A custom title for the graph. By default, it is
+set to "Consonance Function". In order to set a title, it must
+be in quotes. For example, plot_compare(type = "c",
+data = x, title = "Custom Title").}
+
+\item{subtitle}{A custom subtitle for the graph. By default, it is set
+to "The function contains consonance/confidence intervals at every level
+and the P-values." In order to set a subtitle, it must be in quotes.
+For example, plot_compare(type = "c", data = x, subtitle = "Custom Subtitle").}
+
+\item{xaxis}{A custom x-axis title for the graph. By default,
+it is set to "Range of Values.
+In order to set a x-axis title, it must be in quotes. For example,
+plot_compare(type = "c", data = x, xaxis = "Hazard Ratio").}
+
+\item{yaxis}{A custom y-axis title for the graph. By default,
+it is set to "Consonance Level".
+In order to set a y-axis title, it must be in quotes. For example,
+plot_compare(type = "c", data = x, yxis = "Confidence Level").}
+
+\item{color}{Item that allows the user to choose the color of the points
+and the ribbons in the graph. By default, it is set to color = "#555555".
+The inputs must be in quotes.
+For example, plot_compare(type = "c", data = x, color = "#333333").}
+
+\item{fill1}{Item that allows the user to choose the color of the ribbons in the graph
+for data1. By default, it is set to fill1 = "#239a98". The inputs must be in quotes.
+For example, plot_compare(type = "c", data = x, fill1 = "#333333").}
+
+\item{fill2}{Item that allows the user to choose the color of the ribbons in the graph
+for data1. By default, it is set to fill2 = "#d46c5b". The inputs must be in quotes.
+For example, plot_compare(type = "c", data = x, fill2 = "#333333").}
+}
+\value{
+A plot that compares two functions.
+}
+\description{
+Compares the p-value/s-value, and likelihood functions using ggplot2 graphics.
+}
+\examples{
+\donttest{
+library(concurve)
+
+GroupA <- rnorm(50)
+GroupB <- rnorm(50)
+RandomData <- data.frame(GroupA, GroupB)
+intervalsdf <- curve_mean(GroupA, GroupB, data = RandomData)
+GroupA2 <- rnorm(50)
+GroupB2 <- rnorm(50)
+RandomData2 <- data.frame(GroupA2, GroupB2)
+model <- lm(GroupA2 ~ GroupB2, data = RandomData2)
+
+randomframe <- curve_gen(model, "GroupB2")
+
+(plot_compare(intervalsdf[[1]], randomframe[[1]], type = "s"))
+}
+
+}
diff --git a/man/plot_concurve.Rd b/man/plot_concurve.Rd
deleted file mode 100644
index e2c8594..0000000
--- a/man/plot_concurve.Rd
+++ /dev/null
@@ -1,87 +0,0 @@
-\name{plot_concurve}
-\alias{plot_concurve}
-
-\title{
-Plots the P- (Consonance) and S-Value (Surprisal) Functions using base R graphics.
-}
-\description{
-Takes the dataframe produced by the interval functions and plots the p-values, s-values, consonance (confidence)
-levels, and the interval estimates to produce p- and s-value functions using base R graphics.
-}
-\usage{
-plot_concurve(type, data, measure, intervals, title, xlab, ylab1, ylab2, fontsize, fill)
-}
-
-\arguments{
- \item{type}{
-Choose whether to plot a "consonance" function or a "surprisal" function. The default option is set to "consonance". The type must be set in quotes, for example plot_concurve(type = "surprisal") or plot_concurve(type = "consonance").
-}
- \item{data}{
-Dataframe where the results from a curve_ function is stored.
-}
- \item{measure}{
-Indicates whether the object has a log transformation or is normal/default. The default setting is "default". If the measure is set to "ratio", it will take logarithmically transformed values and convert them back to normal values in the dataframe. This is typically a setting used for binary outcomes and their measures such as risk ratios, hazard ratios, and odds ratios.
-}
- \item{intervals}{
-Indicates whether the limits for different consonance levels should be plotted on the graph. By default, this is set to FALSE. When set to TRUE, it will plot 50\%, 75\%, 95\%, and 99\% intervals.
-}
-
- \item{title}{
-The title for the graph. By default, it is set to "Consonance Function". In order to set a title, it must be in quotes. For example, plot_concurve(type = "consonance", data = data, title = "Custom Title").
-}
-
- \item{xlab}{
-The label for the x-axis. By default, it is set to "Theta.". In order to set a label, it must be in quotes. For example, plot_concurve(type = "consonance", data = data, xlab = "Custom Caption").
-}
- \item{ylab1}{
-A label for the y-axis on the left side of the graph. By default, it is set to "P-value." In order to set a custom y-axis label, it must be in quotes. For example, plot_concurve(type = "consonance", data = data, ylab1= "Custom y-axis title").
-}
- \item{ylab2}{
-A label for the y-axis on the right side of the graph. By default, it is set to "Confidence Level."" In order to set a custom y-axis label, it must be in quotes. For example, plot_concurve(type = "consonance", data = data, ylab2= "Custom y-axis title").
-}
- \item{fontsize}{
-Controls the font size in the graphs. By default, it is set to size 12.).
-}
-
- \item{fill}{
-Item that allows the user to choose the color of the ribbons in the graph. By default, it is set to color = "#239a98". The inputs must be in quotes.
-}
-}
-
-\value{
-Plot with intervals at every consonance level graphed with their corresponding p- and s-values.
-}
-\references{
-Amrhein V, Trafimow D, Greenland S. Inferential Statistics as Descriptive Statistics:
-There Is No Replication Crisis If We Don’t Expect Replication. Am Stat; 2018.
-
-Greenland S. Valid P-values behave exactly as they should: Some misleading criticisms of P-values
-and their resolution with S-values. Am Stat. 2018;18(136).
-
-Greenland S. The unconditional information in P-values, and its refutational interpretation
-via S-values. 2018.
-
-Shannon CE. A Mathematical Theory of Communication. Bell System Technical Journal.
-1948;27(3):379-423. doi:10.1002/j.1538-7305.1948.tb01338.x
-
-Poole C. Beyond the confidence interval. Am J Public Health. 1987;77(2):195-199.
-
-Sullivan KM, Foster DA. Use of the confidence interval function. Epidemiology. 1990;1(1):39-42.
-
-Rothman KJ, Greenland S, Lash TL, Others. Modern epidemiology. 2008.
-}
-
-\examples{
-# Simulate random data
-
-GroupA <- rnorm(50)
-GroupB <- rnorm(50)
-
-RandomData <- data.frame(GroupA, GroupB)
-RandomModel <- lm(GroupA ~ GroupB, data = RandomData)
-
-intervalsdf <- curve_gen(RandomModel, "GroupB")
-
-plot_concurve(type = "consonance", data = intervalsdf)
-
-}
diff --git a/man/tidyeval.Rd b/man/tidyeval.Rd
new file mode 100644
index 0000000..5b97416
--- /dev/null
+++ b/man/tidyeval.Rd
@@ -0,0 +1,51 @@
+% Generated by roxygen2: do not edit by hand
+% Please edit documentation in R/utils-tidy-eval.R
+\name{tidyeval}
+\alias{tidyeval}
+\alias{expr}
+\alias{enquo}
+\alias{enquos}
+\alias{sym}
+\alias{syms}
+\alias{.data}
+\alias{:=}
+\alias{as_name}
+\alias{as_label}
+\title{Tidy eval helpers}
+\description{
+\itemize{
+\item \code{\link[rlang:quotation]{sym}()} creates a symbol from a string and
+\code{\link[rlang:quotation]{syms}()} creates a list of symbols from a
+character vector.
+\item \code{\link[rlang:quotation]{enquo}()} and
+\code{\link[rlang:quotation]{enquos}()} delay the execution of one or
+several function arguments. \code{enquo()} returns a single quoted
+expression, which is like a blueprint for the delayed computation.
+\code{enquos()} returns a list of such quoted expressions.
+\item \code{\link[rlang:quotation]{expr}()} quotes a new expression \emph{locally}. It
+is mostly useful to build new expressions around arguments
+captured with \code{\link[=enquo]{enquo()}} or \code{\link[=enquos]{enquos()}}:
+\code{expr(mean(!!enquo(arg), na.rm = TRUE))}.
+\item \code{\link[rlang]{as_name}()} transforms a quoted variable name
+into a string. Supplying something else than a quoted variable
+name is an error.
+
+That's unlike \code{\link[rlang]{as_label}()} which also returns
+a single string but supports any kind of R object as input,
+including quoted function calls and vectors. Its purpose is to
+summarise that object into a single label. That label is often
+suitable as a default name.
+
+If you don't know what a quoted expression contains (for instance
+expressions captured with \code{enquo()} could be a variable
+name, a call to a function, or an unquoted constant), then use
+\code{as_label()}. If you know you have quoted a simple variable
+name, or would like to enforce this, use \code{as_name()}.
+}
+
+To learn more about tidy eval and how to use these tools, visit
+\url{https://tidyeval.tidyverse.org} and the
+\href{https://adv-r.hadley.nz/metaprogramming.html}{Metaprogramming
+section} of \href{https://adv-r.hadley.nz}{Advanced R}.
+}
+\keyword{internal}
diff --git a/pkgdown/extra.css b/pkgdown/extra.css
index 0f1be09..e02d945 100644
--- a/pkgdown/extra.css
+++ b/pkgdown/extra.css
@@ -7,8 +7,12 @@ html, body {
.navbar-brand {
font-size: 16px;
font-weight: bold;
+ padding-bottom: 20px;
+ line-height: 32px;
}
+
+
.navbar-default .navbar-nav>li>a:hover,
.navbar-default .navbar-nav>li>a:focus {
background-color: #eee;
@@ -42,7 +46,8 @@ a:focus {
}
h1, .h1 {
- font-size: 32px;
+ font-size: 25px;
+ font-weight: 900;
}
h1 small, .h1 small {
@@ -52,15 +57,15 @@ h1 small, .h1 small {
}
h2, .h2 {
- font-size: 28px;
+ font-size: 25px;
}
h3, .h3 {
- font-size: 20px;
+ font-size: 24px;
}
h4, .h4 {
- font-size: 20px;
+ font-size: 23px;
}
.contents h1, .contents h2, .contents h3, .contents h4 {
@@ -96,3 +101,5 @@ pre code {
color: #eeeeee;
background-color: #d46c5b;
}
+
+
diff --git a/pkgdown/favicon/apple-touch-icon-120x120.png b/pkgdown/favicon/apple-touch-icon-120x120.png
index 3ee0b4e..1f19bf9 100644
Binary files a/pkgdown/favicon/apple-touch-icon-120x120.png and b/pkgdown/favicon/apple-touch-icon-120x120.png differ
diff --git a/pkgdown/favicon/apple-touch-icon-152x152.png b/pkgdown/favicon/apple-touch-icon-152x152.png
index 37275f0..ba2a7da 100644
Binary files a/pkgdown/favicon/apple-touch-icon-152x152.png and b/pkgdown/favicon/apple-touch-icon-152x152.png differ
diff --git a/pkgdown/favicon/apple-touch-icon-180x180.png b/pkgdown/favicon/apple-touch-icon-180x180.png
index 9f04ece..0c951f2 100644
Binary files a/pkgdown/favicon/apple-touch-icon-180x180.png and b/pkgdown/favicon/apple-touch-icon-180x180.png differ
diff --git a/pkgdown/favicon/apple-touch-icon-60x60.png b/pkgdown/favicon/apple-touch-icon-60x60.png
index 0eb1103..f51ee46 100644
Binary files a/pkgdown/favicon/apple-touch-icon-60x60.png and b/pkgdown/favicon/apple-touch-icon-60x60.png differ
diff --git a/pkgdown/favicon/apple-touch-icon-76x76.png b/pkgdown/favicon/apple-touch-icon-76x76.png
index fae2d7c..0c74ab0 100644
Binary files a/pkgdown/favicon/apple-touch-icon-76x76.png and b/pkgdown/favicon/apple-touch-icon-76x76.png differ
diff --git a/pkgdown/favicon/apple-touch-icon.png b/pkgdown/favicon/apple-touch-icon.png
index 9f04ece..675caa2 100644
Binary files a/pkgdown/favicon/apple-touch-icon.png and b/pkgdown/favicon/apple-touch-icon.png differ
diff --git a/pkgdown/favicon/favicon-16x16.png b/pkgdown/favicon/favicon-16x16.png
index 1033bac..930e22d 100644
Binary files a/pkgdown/favicon/favicon-16x16.png and b/pkgdown/favicon/favicon-16x16.png differ
diff --git a/pkgdown/favicon/favicon-32x32.png b/pkgdown/favicon/favicon-32x32.png
index e69a312..9c4de3c 100644
Binary files a/pkgdown/favicon/favicon-32x32.png and b/pkgdown/favicon/favicon-32x32.png differ
diff --git a/revdep/.gitignore b/revdep/.gitignore
new file mode 100644
index 0000000..31f6c40
--- /dev/null
+++ b/revdep/.gitignore
@@ -0,0 +1,6 @@
+checks
+library
+checks.noindex
+library.noindex
+data.sqlite
+*.html
diff --git a/revdep/email.yml b/revdep/email.yml
new file mode 100644
index 0000000..0c5cef8
--- /dev/null
+++ b/revdep/email.yml
@@ -0,0 +1,5 @@
+release_date: ???
+rel_release_date: ???
+my_news_url: ???
+release_version: ???
+release_details: ???
diff --git a/tests/spelling.R b/tests/spelling.R
new file mode 100644
index 0000000..13f77d9
--- /dev/null
+++ b/tests/spelling.R
@@ -0,0 +1,6 @@
+if (requireNamespace("spelling", quietly = TRUE)) {
+ spelling::spell_check_test(
+ vignettes = TRUE, error = FALSE,
+ skip_on_cran = TRUE
+ )
+}
diff --git a/tests/testthat/testdfstructure.R b/tests/testthat/testdfstructure.R
index 2983b31..c3060d9 100644
--- a/tests/testthat/testdfstructure.R
+++ b/tests/testthat/testdfstructure.R
@@ -1,14 +1,17 @@
+
+
context("Dataframe Structure")
test_that("curve_mean", {
library(concurve)
+
# Produce random sample data
GroupA <- runif(100, min = 0, max = 100)
GroupB <- runif(100, min = 0, max = 100)
RandomData <- data.frame(GroupA, GroupB)
- bob <- curve_mean(GroupA, GroupB, RandomData)
+ bob <- curve_mean(GroupA, GroupB, RandomData, method = "default")
# Set sample dataframe.
variable1 <- rnorm(100)
@@ -16,19 +19,23 @@ test_that("curve_mean", {
variable3 <- rnorm(100)
variable4 <- rnorm(100)
variable5 <- rnorm(100)
+ variable6 <- rnorm(100)
+ variable7 <- rnorm(100)
- sampledf <- data.frame(variable1, variable2, variable3, variable4, variable5)
+ sampledf <- data.frame(variable1, variable2, variable3, variable4, variable5, variable6, variable7)
- columnnames <- c("lower.limit", "upper.limit", "intrvl.level", "pvalue", "svalue")
+ columnnames <- c("lower.limit", "upper.limit", "intrvl.width", "intrvl.level", "cdf", "pvalue", "svalue")
colnames(sampledf) <- columnnames
- expect_equivalent(str(bob), str(sampledf))
+ expect_equivalent(str(bob[[1]]), str(sampledf))
})
test_that("curve_gen", {
library(concurve)
+
+
# Produce random sample data
GroupA <- rnorm(50)
GroupB <- rnorm(50)
@@ -36,7 +43,7 @@ test_that("curve_gen", {
RandomData <- data.frame(GroupA, GroupB)
rob <- glm(GroupA ~ GroupB, data = RandomData)
- bob <- curve_gen(rob, "GroupB", method = "lm")
+ bob <- curve_gen(rob, "GroupB", method = "glm")
# Set sample dataframe.
variable1 <- rnorm(100)
@@ -44,20 +51,23 @@ test_that("curve_gen", {
variable3 <- rnorm(100)
variable4 <- rnorm(100)
variable5 <- rnorm(100)
+ variable6 <- rnorm(100)
+ variable7 <- rnorm(100)
- sampledf <- data.frame(variable1, variable2, variable3, variable4, variable5)
+ sampledf <- data.frame(variable1, variable2, variable3, variable4, variable5, variable6, variable7)
- columnnames <- c("lower.limit", "upper.limit", "intrvl.level", "pvalue", "svalue")
+ columnnames <- c("lower.limit", "upper.limit", "intrvl.width", "intrvl.level", "cdf", "pvalue", "svalue")
colnames(sampledf) <- columnnames
- expect_equivalent(str(bob), str(sampledf))
+ expect_equivalent(str(bob[[1]]), str(sampledf))
})
test_that("curve_meta", {
library(concurve)
library(metafor)
+
# Produce random sample data
GroupAData <- runif(20, min = 0, max = 100)
GroupAMean <- round(mean(GroupAData), digits = 2)
@@ -110,12 +120,14 @@ test_that("curve_meta", {
variable3 <- rnorm(100)
variable4 <- rnorm(100)
variable5 <- rnorm(100)
+ variable6 <- rnorm(100)
+ variable7 <- rnorm(100)
- sampledf <- data.frame(variable1, variable2, variable3, variable4, variable5)
+ sampledf <- data.frame(variable1, variable2, variable3, variable4, variable5, variable6, variable7)
- columnnames <- c("lower.limit", "upper.limit", "intrvl.level", "pvalue", "svalue")
+ columnnames <- c("lower.limit", "upper.limit", "intrvl.width", "intrvl.level", "cdf", "pvalue", "svalue")
colnames(sampledf) <- columnnames
- expect_equivalent(str(metaf), str(sampledf))
+ expect_equivalent(str(metaf[[1]]), str(sampledf))
})
diff --git a/usethis.R b/usethis.R
new file mode 100644
index 0000000..a46524e
--- /dev/null
+++ b/usethis.R
@@ -0,0 +1,46 @@
+# Importing other packages
+
+use_package("MASS", "Imports", min_version = NULL)
+use_package("parallel", "Imports", min_version = NULL)
+use_package("pbmcapply", "Imports", min_version = NULL)
+use_package("compiler", "Imports", min_version = NULL)
+use_package("boot", "Imports", min_version = NULL)
+use_package("bcaboot", "Imports", min_version = NULL)
+use_package("ProfileLikelihood", "Imports", min_version = NULL)
+use_package("ggplot2", "Imports", min_version = NULL)
+use_package("metafor", "Imports", min_version = NULL)
+use_package("dplyr", "Imports", min_version = NULL)
+use_package("tidyr", "Imports", min_version = NULL)
+use_package("flextable", "Imports", min_version = NULL)
+use_package("officer", "Imports", min_version = NULL)
+use_package("knitr", "Imports", min_version = NULL)
+use_package("tibble", "Imports", min_version = NULL)
+use_package("survival", "Imports", min_version = NULL)
+use_package("survminer", "Imports", min_version = NULL)
+use_package("scales", "Imports", min_version = NULL)
+
+# Suggest other packages
+use_package("testthat", "Suggests", min_version = NULL)
+use_package("covr", "Suggests", min_version = NULL)
+use_package("spelling", "Suggests", min_version = NULL)
+use_package("Lock5Data", "Suggests", min_version = NULL)
+
+# Other helper functions
+
+use_build_ignore("usethis.R", escape = TRUE)
+use_build_ignore("references.bib", escape = TRUE)
+use_build_ignore("american-medical-association.csl", escape = TRUE)
+
+use_spell_check(vignettes = TRUE, lang = "en-US", error = FALSE)
+use_cran_comments(open = interactive())
+use_tidy_style()
+use_revdep()
+
+check_rhub(pkg = ".", platforms = NULL, email = NULL,
+ interactive = TRUE, build_args = NULL)
+
+check(pkg = ".", document = NA, build_args = NULL,
+ manual = TRUE, cran = TRUE, remote = TRUE, incoming = TRUE,
+ force_suggests = TRUE, run_dont_test = TRUE, args = "--timings",
+ env_vars = NULL, quiet = FALSE, check_dir = tempdir(),
+ cleanup = TRUE, error_on = c("never", "error", "warning", "note"))
diff --git a/vignettes/.gitignore b/vignettes/.gitignore
new file mode 100644
index 0000000..097b241
--- /dev/null
+++ b/vignettes/.gitignore
@@ -0,0 +1,2 @@
+*.html
+*.R
diff --git a/vignettes/american-medical-association.csl b/vignettes/american-medical-association.csl
new file mode 100755
index 0000000..78e5311
--- /dev/null
+++ b/vignettes/american-medical-association.csl
@@ -0,0 +1,276 @@
+
+
diff --git a/vignettes/examples.Rmd b/vignettes/examples.Rmd
index 5f91040..30e17b9 100644
--- a/vignettes/examples.Rmd
+++ b/vignettes/examples.Rmd
@@ -1,6 +1,9 @@
---
title: "Examples in R"
output: rmarkdown::html_vignette
+bibliography: references.bib
+link-citations: yes
+csl: american-medical-association.csl
vignette: >
%\VignetteIndexEntry{Examples in R}
%\VignetteEngine{knitr::rmarkdown}
@@ -9,326 +12,279 @@ vignette: >
```{r setup, include = FALSE}
knitr::opts_chunk$set(
- collapse = TRUE,
- comment = "#>"
+ message = TRUE,
+ warning = TRUE,
+ collapse = TRUE,
+ comment = "#>"
)
```
-## Using Mean Differences
+## Introduction
-If we were to generate some random data from a normal distribution with
-the following code,
+Here I show how to produce _P_-value, _S_-value, likelihood, and deviance functions with the `concurve` package using fake data and data from real studies. Simply put, these functions are rich sources of information for scientific inference and the image below, taken from Xie & Singh, 2013[@xie2013isr] displays why.
-``` r
-GroupA <- rnorm(20)
-GroupB <- rnorm(20)
+ +For a more extensive discussion of these concepts, see the following references. [@birnbaum1961ams; @chow2019asb; @fraser2017arsa; @fraser2019as; @Poole1987-nb; @poole1987ajph; @Schweder2002-vh; @schweder2016; @Singh2007-zr; @Sullivan1990-ha; @whitehead1993sm; @xie2013isr; @rothman2008me]
+
+To get started, we could generate some normal data and combine two vectors in a dataframe
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+library(concurve)
+set.seed(1031)
+GroupA <- rnorm(500)
+GroupB <- rnorm(500)
RandomData <- data.frame(GroupA, GroupB)
```
-and compare the means of these two "groups" using a t-test,
+and look at the differences between the two vectors. We'll plug these vectors and the dataframe they're in inside of the `curve_mean()` function. Here, the default method involves calculating CIs using the Wald method.
-```r
-testresults <- t.test(GroupA, GroupB, data = RandomData, paired = FALSE)
+``` {r}
+intervalsdf <- curve_mean(GroupA, GroupB,
+ data = RandomData, method = "default"
+)
```
-we would likely see some differences, given that we have such a small
-sample in each group.
-```r
-summary(testresults)
+Each of the functions within `concurve` will generally produce a list with three items, and the first will usually contain the function of interest.
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+tibble::tibble(intervalsdf[[1]])
```
-We can see our P-value for the statistical test along with the computed
-95% interval with the command above (which is given to us by default by the program). Thus,
-effect sizes that range from the lower bound of this interval to the
-upper bound are compatible with the test model at this consonance
-level.
+We can view the function using the `ggcurve()` function. The two basic arguments that must be provided are the data argument and the "type" argument. To plot a consonance function, we would write "c".
-However, as stated before, a 95% interval is only an artifact of the
-commonly used 5% alpha level for hypothesis testing and is nowhere near
-as informative as a function.
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(function1 <- ggcurve(data = intervalsdf[[1]], type = "c"))
+```
-If we were to take the information from this data and calculate a
-P-value function where every single consonance interval and its
-corresponding P-value were plotted, we would be able to see the full
-range of effect sizes compatible with the test model at various levels.
+We can see that the consonance "curve" is every interval estimate plotted, and provides the _P_-values, CIs, along with the median unbiased estimate It can be defined as such,
-It is relatively easy to produce such a function using the
-[**concurve**](https://github.com/Zadchow/concurve)
-package in R.
+$$C V_{n}(\theta)=1-2\left|H_{n}(\theta)-0.5\right|=2 \min \left\{H_{n}(\theta), 1-H_{n}(\theta)\right\}$$
-Install the package directly from [CRAN](https://cran.r-project.org/package=concurve)
+Its information counterpart, the surprisal function, can be constructed by taking the $-log_{2}$ of the _P_-value.[@chow2019asb; @greenland2019as; @Shannon1948-uq]
-``` r
-install.packages("concurve")
-```
-or get a more slightly up-to-date version via GitHub.
+To view the surprisal function, we simply change the type to "s".
-``` r
-library(devtools)
-install_github("zadchow/concurve")
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(function1 <- ggcurve(data = intervalsdf[[1]], type = "s"))
```
-We’ll use the same data from above to calculate a P-value function and
-since we are focusing on mean differences using a t-test, we will use
-the `curve_meta()` function to calculate our consonance
-intervals and store them in a dataframe.
-``` r
-library(concurve)
-intervalsdf <- curve_mean(GroupA, GroupB,
- data = RandomData, method = "default"
-)
-```
+We can also view the consonance distribution by changing the type to "cdf", which is a cumulative probability distribution. The point at which the curve reaches 50% is known as the "median unbiased estimate". It is the same estimate that is typically at the peak of the _P_-value curve from above.
-Now thousands of consonance intervals at various levels have been
-stored in the dataframe “intervalsdf.” We can preview some of the entries
-via the `tibble` package.
-```r
-tibble::tibble(intervalsdf)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(function1s <- ggcurve(data = intervalsdf[[2]], type = "cdf"))
```
-There's a quick look at the first few entries of our dataframe.
-
-We can plot this data using the `ggconcurve()` function.
+We can also get relevant statistics that show the range of values by using the `curve_table()` function. There are several formats that can be exported such as .docx, .ppt, and TeX.
-``` r
-pfunction <- ggconcurve(type = "consonance", intervalsdf)
-pfunction
+```{r echo=TRUE, fig.height=2, fig.width=4}
+(x <- curve_table(data = intervalsdf[[1]], format = "image"))
```
-
-
+For a more extensive discussion of these concepts, see the following references. [@birnbaum1961ams; @chow2019asb; @fraser2017arsa; @fraser2019as; @Poole1987-nb; @poole1987ajph; @Schweder2002-vh; @schweder2016; @Singh2007-zr; @Sullivan1990-ha; @whitehead1993sm; @xie2013isr; @rothman2008me]
+
+To get started, we could generate some normal data and combine two vectors in a dataframe
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+library(concurve)
+set.seed(1031)
+GroupA <- rnorm(500)
+GroupB <- rnorm(500)
RandomData <- data.frame(GroupA, GroupB)
```
-and compare the means of these two "groups" using a t-test,
+and look at the differences between the two vectors. We'll plug these vectors and the dataframe they're in inside of the `curve_mean()` function. Here, the default method involves calculating CIs using the Wald method.
-```r
-testresults <- t.test(GroupA, GroupB, data = RandomData, paired = FALSE)
+``` {r}
+intervalsdf <- curve_mean(GroupA, GroupB,
+ data = RandomData, method = "default"
+)
```
-we would likely see some differences, given that we have such a small
-sample in each group.
-```r
-summary(testresults)
+Each of the functions within `concurve` will generally produce a list with three items, and the first will usually contain the function of interest.
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+tibble::tibble(intervalsdf[[1]])
```
-We can see our P-value for the statistical test along with the computed
-95% interval with the command above (which is given to us by default by the program). Thus,
-effect sizes that range from the lower bound of this interval to the
-upper bound are compatible with the test model at this consonance
-level.
+We can view the function using the `ggcurve()` function. The two basic arguments that must be provided are the data argument and the "type" argument. To plot a consonance function, we would write "c".
-However, as stated before, a 95% interval is only an artifact of the
-commonly used 5% alpha level for hypothesis testing and is nowhere near
-as informative as a function.
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(function1 <- ggcurve(data = intervalsdf[[1]], type = "c"))
+```
-If we were to take the information from this data and calculate a
-P-value function where every single consonance interval and its
-corresponding P-value were plotted, we would be able to see the full
-range of effect sizes compatible with the test model at various levels.
+We can see that the consonance "curve" is every interval estimate plotted, and provides the _P_-values, CIs, along with the median unbiased estimate It can be defined as such,
-It is relatively easy to produce such a function using the
-[**concurve**](https://github.com/Zadchow/concurve)
-package in R.
+$$C V_{n}(\theta)=1-2\left|H_{n}(\theta)-0.5\right|=2 \min \left\{H_{n}(\theta), 1-H_{n}(\theta)\right\}$$
-Install the package directly from [CRAN](https://cran.r-project.org/package=concurve)
+Its information counterpart, the surprisal function, can be constructed by taking the $-log_{2}$ of the _P_-value.[@chow2019asb; @greenland2019as; @Shannon1948-uq]
-``` r
-install.packages("concurve")
-```
-or get a more slightly up-to-date version via GitHub.
+To view the surprisal function, we simply change the type to "s".
-``` r
-library(devtools)
-install_github("zadchow/concurve")
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(function1 <- ggcurve(data = intervalsdf[[1]], type = "s"))
```
-We’ll use the same data from above to calculate a P-value function and
-since we are focusing on mean differences using a t-test, we will use
-the `curve_meta()` function to calculate our consonance
-intervals and store them in a dataframe.
-``` r
-library(concurve)
-intervalsdf <- curve_mean(GroupA, GroupB,
- data = RandomData, method = "default"
-)
-```
+We can also view the consonance distribution by changing the type to "cdf", which is a cumulative probability distribution. The point at which the curve reaches 50% is known as the "median unbiased estimate". It is the same estimate that is typically at the peak of the _P_-value curve from above.
-Now thousands of consonance intervals at various levels have been
-stored in the dataframe “intervalsdf.” We can preview some of the entries
-via the `tibble` package.
-```r
-tibble::tibble(intervalsdf)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(function1s <- ggcurve(data = intervalsdf[[2]], type = "cdf"))
```
-There's a quick look at the first few entries of our dataframe.
-
-We can plot this data using the `ggconcurve()` function.
+We can also get relevant statistics that show the range of values by using the `curve_table()` function. There are several formats that can be exported such as .docx, .ppt, and TeX.
-``` r
-pfunction <- ggconcurve(type = "consonance", intervalsdf)
-pfunction
+```{r echo=TRUE, fig.height=2, fig.width=4}
+(x <- curve_table(data = intervalsdf[[1]], format = "image"))
```
-
- -
-
-Now we can see every consonance interval and its corresponding
-P-value and consonance level plotted. As stated before, a single 95%
-consonance interval is simply a slice through this function, which
-provides far more information as to what is compatible with the test
-model and its assumptions.
-
-Furthermore, we can also produce a "surprisal" function by plotting every consonance interval and its corresponding
-[***S-value***](https://lesslikely.com/statistics/s-values/)
-using the `ggconcurve()` function with type being set as "surprisal".
-
-``` r
-sfunction <- ggconcurve(type = "surprisal", intervalsdf)
-sfunction
-```
-
-
-
-
-
-Now we can see every consonance interval and its corresponding
-P-value and consonance level plotted. As stated before, a single 95%
-consonance interval is simply a slice through this function, which
-provides far more information as to what is compatible with the test
-model and its assumptions.
-
-Furthermore, we can also produce a "surprisal" function by plotting every consonance interval and its corresponding
-[***S-value***](https://lesslikely.com/statistics/s-values/)
-using the `ggconcurve()` function with type being set as "surprisal".
-
-``` r
-sfunction <- ggconcurve(type = "surprisal", intervalsdf)
-sfunction
-```
-
-
- -
-
-The graph from the code above provides us with consonance levels and the maximum
-amount of information against the effect sizes contained in the
-consonance interval.
-## Simple Linear Models
+# Comparing Functions
-We can also try this with other simple linear models.
+If we wanted to compare two studies to see the amount of "consonance", we could use the `curve_compare()` function to get a numerical output.
-Let’s simulate more normal data and fit a simple linear regression to it
-using ordinary least squares regression with the base R `lm()` function.
+First, we generate some more fake data
-``` r
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
GroupA2 <- rnorm(500)
GroupB2 <- rnorm(500)
-
RandomData2 <- data.frame(GroupA2, GroupB2)
-
model <- lm(GroupA2 ~ GroupB2, data = RandomData2)
+randomframe <- curve_gen(model, "GroupB2")
+```
+
+Once again, we'll plot this data with `ggcurve()`. We can also indicate whether we want certain interval estimates to be plotted in the function with the "levels" argument. If we wanted to plot the 50%, 75%, and 95% intervals, we'd provide the argument this way:
-summary(model)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(function2 <- ggcurve(type = "c", randomframe[[1]], levels = c(0.50, 0.75, 0.95), nullvalue = TRUE))
```
-We can see some of the basic statistics of our model including the 95%
-interval for our predictor (GroupB). Perhaps we want more information.
-Well we can do that! Using the `curve_gen()`, we can calculate several
-consonance intervals for the regression coefficient and then plot the
-consonance and surprisal functions.
+Now that we have two datasets and two functions, we can compare them using the `curve_compare()` function.
-``` r
-randomframe <- curve_gen(model, "GroupB2")
-tibble::tibble(randomframe)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(curve_compare(
+ data1 = intervalsdf[[1]], data2 = randomframe[[1]], type = "c",
+ plot = TRUE, measure = "default", nullvalue = TRUE
+))
```
-Now that we have our data frame, we can graph our function.
+This function will provide us with the area that is shared between the curve, along with a ratio of overlap to non-overlap.
-``` r
-ggconcurve(type = "consonance", randomframe)
+We can also do this for the surprisal function simply by changing type to "s".
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(curve_compare(
+ data1 = intervalsdf[[1]], data2 = randomframe[[1]], type = "s",
+ plot = TRUE, measure = "default", nullvalue = FALSE
+))
```
-
-
-
-
-The graph from the code above provides us with consonance levels and the maximum
-amount of information against the effect sizes contained in the
-consonance interval.
-## Simple Linear Models
+# Comparing Functions
-We can also try this with other simple linear models.
+If we wanted to compare two studies to see the amount of "consonance", we could use the `curve_compare()` function to get a numerical output.
-Let’s simulate more normal data and fit a simple linear regression to it
-using ordinary least squares regression with the base R `lm()` function.
+First, we generate some more fake data
-``` r
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
GroupA2 <- rnorm(500)
GroupB2 <- rnorm(500)
-
RandomData2 <- data.frame(GroupA2, GroupB2)
-
model <- lm(GroupA2 ~ GroupB2, data = RandomData2)
+randomframe <- curve_gen(model, "GroupB2")
+```
+
+Once again, we'll plot this data with `ggcurve()`. We can also indicate whether we want certain interval estimates to be plotted in the function with the "levels" argument. If we wanted to plot the 50%, 75%, and 95% intervals, we'd provide the argument this way:
-summary(model)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(function2 <- ggcurve(type = "c", randomframe[[1]], levels = c(0.50, 0.75, 0.95), nullvalue = TRUE))
```
-We can see some of the basic statistics of our model including the 95%
-interval for our predictor (GroupB). Perhaps we want more information.
-Well we can do that! Using the `curve_gen()`, we can calculate several
-consonance intervals for the regression coefficient and then plot the
-consonance and surprisal functions.
+Now that we have two datasets and two functions, we can compare them using the `curve_compare()` function.
-``` r
-randomframe <- curve_gen(model, "GroupB2")
-tibble::tibble(randomframe)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(curve_compare(
+ data1 = intervalsdf[[1]], data2 = randomframe[[1]], type = "c",
+ plot = TRUE, measure = "default", nullvalue = TRUE
+))
```
-Now that we have our data frame, we can graph our function.
+This function will provide us with the area that is shared between the curve, along with a ratio of overlap to non-overlap.
-``` r
-ggconcurve(type = "consonance", randomframe)
+We can also do this for the surprisal function simply by changing type to "s".
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(curve_compare(
+ data1 = intervalsdf[[1]], data2 = randomframe[[1]], type = "s",
+ plot = TRUE, measure = "default", nullvalue = FALSE
+))
```
-
- -
+It's clear that the outputs have changed and indicate far more overlap than before.
+
+# Constructing Functions From Single Intervals
+
+We can also take a set of confidence limits and use them to construct a consonance, surprisal, likelihood or deviance function using the `curve_rev()` function.
-``` r
-s <- ggconcurve(type = "surprisal", randomframe)
-s
+Here, we'll use two epidemiological studies[@brown2017j; @brown2017jcp] that studied the impact of SSRI exposure in pregnant mothers, and the rate of autism in children.
+
+Both of these studies suggested a null effect of SSRI exposure on autism rates in children.
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+curve1 <- curve_rev(point = 1.7, LL = 1.1, UL = 2.6, type = "c", measure = "ratio", steps = 10000)
+(ggcurve(data = curve1[[1]], type = "c", measure = "ratio", nullvalue = TRUE))
+curve2 <- curve_rev(point = 1.61, LL = 0.997, UL = 2.59,type = "c", measure = "ratio", steps = 10000)
+(ggcurve(data = curve2[[1]], type = "c", measure = "ratio", nullvalue = TRUE))
```
-
-
-
+It's clear that the outputs have changed and indicate far more overlap than before.
+
+# Constructing Functions From Single Intervals
+
+We can also take a set of confidence limits and use them to construct a consonance, surprisal, likelihood or deviance function using the `curve_rev()` function.
-``` r
-s <- ggconcurve(type = "surprisal", randomframe)
-s
+Here, we'll use two epidemiological studies[@brown2017j; @brown2017jcp] that studied the impact of SSRI exposure in pregnant mothers, and the rate of autism in children.
+
+Both of these studies suggested a null effect of SSRI exposure on autism rates in children.
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+curve1 <- curve_rev(point = 1.7, LL = 1.1, UL = 2.6, type = "c", measure = "ratio", steps = 10000)
+(ggcurve(data = curve1[[1]], type = "c", measure = "ratio", nullvalue = TRUE))
+curve2 <- curve_rev(point = 1.61, LL = 0.997, UL = 2.59,type = "c", measure = "ratio", steps = 10000)
+(ggcurve(data = curve2[[1]], type = "c", measure = "ratio", nullvalue = TRUE))
```
-
- -
+The null value is shown via the red line and it's clear that a large mass of the function is away from it.
-We can also compare these functions to likelihood functions (also called
-support intervals), and we’ll see that we get very similar results.
-We’ll do this using the ***ProfileLikelihood*** package.
+We can also see this by plotting the likelihood functions via the `curve_rev()` function.
-``` r
-xx <- profilelike.lm(
- formula = GroupA2 ~ 1, data = RandomData2,
- profile.theta = "GroupB2",
- lo.theta = -0.3, hi.theta = 0.3, length = 500
-)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+lik1 <- curve_rev(point = 1.7, LL = 1.1, UL = 2.6, type = "l", measure = "ratio", steps = 10000)
+(ggcurve(data = lik1[[1]], type = "l1", measure = "ratio", nullvalue = TRUE))
+lik2 <- curve_rev(point = 1.61, LL = 0.997, UL = 2.59,type = "l", measure = "ratio", steps = 10000)
+(ggcurve(data = lik2[[1]], type = "l1", measure = "ratio", nullvalue = TRUE))
```
-Now we plot our likelihood function and we can see what the maximum
-likelihood estimation is. Notice that it’s practically similar to the
-interval in the S-value function with 0 bits of information against it
-and and the consonance interval in the P-value function with a
-P-value of 1.
+We can also view the amount of agreement between the likelihood functions of these two studies.
-``` r
-profilelike.plot(
- theta = xx$theta,
- profile.lik.norm = xx$profile.lik.norm, round = 3
-)
-title(main = "Likelihood Function")
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(plot_compare(
+ data1 = lik1[[1]], data2 = lik2[[1]], type = "l1", measure = "ratio", nullvalue = TRUE, title = "Brown et al. 2017. J Clin Psychiatry. vs. \nBrown et al. 2017. JAMA.",
+ subtitle = "J Clin Psychiatry: OR = 1.7, 1/6.83 LI: LL = 1.1, UL = 2.6 \nJAMA: HR = 1.61, 1/6.83 LI: LL = 0.997, UL = 2.59", xaxis = expression(Theta ~ "= Hazard Ratio / Odds Ratio")
+))
```
-
-
-
+The null value is shown via the red line and it's clear that a large mass of the function is away from it.
-We can also compare these functions to likelihood functions (also called
-support intervals), and we’ll see that we get very similar results.
-We’ll do this using the ***ProfileLikelihood*** package.
+We can also see this by plotting the likelihood functions via the `curve_rev()` function.
-``` r
-xx <- profilelike.lm(
- formula = GroupA2 ~ 1, data = RandomData2,
- profile.theta = "GroupB2",
- lo.theta = -0.3, hi.theta = 0.3, length = 500
-)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+lik1 <- curve_rev(point = 1.7, LL = 1.1, UL = 2.6, type = "l", measure = "ratio", steps = 10000)
+(ggcurve(data = lik1[[1]], type = "l1", measure = "ratio", nullvalue = TRUE))
+lik2 <- curve_rev(point = 1.61, LL = 0.997, UL = 2.59,type = "l", measure = "ratio", steps = 10000)
+(ggcurve(data = lik2[[1]], type = "l1", measure = "ratio", nullvalue = TRUE))
```
-Now we plot our likelihood function and we can see what the maximum
-likelihood estimation is. Notice that it’s practically similar to the
-interval in the S-value function with 0 bits of information against it
-and and the consonance interval in the P-value function with a
-P-value of 1.
+We can also view the amount of agreement between the likelihood functions of these two studies.
-``` r
-profilelike.plot(
- theta = xx$theta,
- profile.lik.norm = xx$profile.lik.norm, round = 3
-)
-title(main = "Likelihood Function")
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(plot_compare(
+ data1 = lik1[[1]], data2 = lik2[[1]], type = "l1", measure = "ratio", nullvalue = TRUE, title = "Brown et al. 2017. J Clin Psychiatry. vs. \nBrown et al. 2017. JAMA.",
+ subtitle = "J Clin Psychiatry: OR = 1.7, 1/6.83 LI: LL = 1.1, UL = 2.6 \nJAMA: HR = 1.61, 1/6.83 LI: LL = 0.997, UL = 2.59", xaxis = expression(Theta ~ "= Hazard Ratio / Odds Ratio")
+))
```
-
- -
+and the consonance functions
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(plot_compare(
+ data1 = curve1[[1]], data2 = curve2[[1]], type = "c", measure = "ratio", nullvalue = TRUE, title = "Brown et al. 2017. J Clin Psychiatry. vs. \nBrown et al. 2017. JAMA.",
+ subtitle = "J Clin Psychiatry: OR = 1.7, 1/6.83 LI: LL = 1.1, UL = 2.6 \nJAMA: HR = 1.61, 1/6.83 LI: LL = 0.997, UL = 2.59", xaxis = expression(Theta ~ "= Hazard Ratio / Odds Ratio")
+))
+```
-We’ve used a relatively easy example for this blog post, but the
-[**concurve**](https://github.com/Zadchow/concurve)
-package is also able to calculate consonance functions for multiple
-regressions, logistic regressions, ANOVAs, and meta-analyses (that have
-been produced by the ***metafor*** package).
+# The Bootstrap and Consonance Functions
-## Using Meta-Analysis Data
+Some authors have shown that the bootstrap distribution is equal to the confidence distribution because it meets the definition of a consonance distribution.[@efron1994; @efron2018; @xie2013isr] The bootstrap distribution and the asymptotic consonance distribution would be defined as:
-Here we present another quick example with a meta-analysis of simulated
-data.
+$$H_{n}(\theta)=1-P\left(\hat{\theta}-\hat{\theta}^{*} \leq \hat{\theta}-\theta | \mathbf{x}\right)=P\left(\hat{\theta}^{*} \leq \theta | \mathbf{x}\right)$$
-First, we generate random data for two groups in two hypothetical
-studies
+Certain bootstrap methods such as the BCa method and _t_-bootstrap method also yield second order accuracy of consonance distributions.
-``` r
-GroupAData <- runif(20, min = 0, max = 100)
-GroupAMean <- round(mean(GroupAData), digits = 2)
-GroupASD <- round(sd(GroupAData), digits = 2)
+$$H_{n}(\theta)=1-P\left(\frac{\hat{\theta}^{*}-\hat{\theta}}{\widehat{S E}^{*}\left(\hat{\theta}^{*}\right)} \leq \frac{\hat{\theta}-\theta}{\widehat{S E}(\hat{\theta})} | \mathbf{x}\right)$$
-GroupBData <- runif(20, min = 0, max = 100)
-GroupBMean <- round(mean(GroupBData), digits = 2)
-GroupBSD <- round(sd(GroupBData), digits = 2)
+Here, I demonstrate how to use these particular bootstrap methods to arrive at consonance curves and densities.
-GroupCData <- runif(20, min = 0, max = 100)
-GroupCMean <- round(mean(GroupCData), digits = 2)
-GroupCSD <- round(sd(GroupCData), digits = 2)
+We'll use the Iris dataset and construct a function that'll yield a parameter of interest.
-GroupDData <- runif(20, min = 0, max = 100)
-GroupDMean <- round(mean(GroupDData), digits = 2)
-GroupDSD <- round(sd(GroupDData), digits = 2)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+iris <- datasets::iris
+foo <- function(data, indices) {
+ dt <- data[indices, ]
+ c(
+ cor(dt[, 1], dt[, 2], method = "p")
+ )
+}
```
-We can then quickly combine the data in a dataframe.
-
-``` r
-StudyName <- c("Study1", "Study2")
-MeanTreatment <- c(GroupAMean, GroupCMean)
-MeanControl <- c(GroupBMean, GroupDMean)
-SDTreatment <- c(GroupASD, GroupCSD)
-SDControl <- c(GroupBSD, GroupDSD)
-NTreatment <- c(20, 20)
-NControl <- c(20, 20)
-
-metadf <- data.frame(
- StudyName, MeanTreatment, MeanControl,
- SDTreatment, SDControl,
- NTreatment, NControl
-)
+We can now use the `curve_boot()` method to construct a function. The default method used for this function is the "BCa" method provided by the [`bcaboot`](https://cran.r-project.org/package=bcaboot) package.[@efron2018]
+
+```{r include=FALSE}
+y <- curve_boot(data = iris, func = foo, method = "bca", replicates = 2000, steps = 1000)
```
-Then, we’ll use ***metafor*** to calculate the standardized mean
-difference.
+I will suppress the output of the function because it is unnecessarily long. But we've placed all the estimates into a list object called y.
-``` r
-dat <- escalc(
- measure = "SMD",
- m1i = MeanTreatment, sd1i = SDTreatment, n1i = NTreatment,
- m2i = MeanControl, sd2i = SDControl, n2i = NControl,
- data = metadf
-)
+The first item in the list will be the consonance distribution constructed by typical means, while the third item will be the bootstrap approximation to the consonance distribution.
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+ggcurve(data = y[[1]])
+ggcurve(data = y[[3]])
```
-Next, we’ll pool the data using a ~~fixed-effects~~ common-effects model
+We can also print out a table for TeX documents
-``` r
-res <- rma(yi, vi,
- data = dat, slab = paste(StudyName, sep = ", "),
- method = "FE", digits = 2
-)
+```{r echo=TRUE, fig.height=2, fig.width=4}
+(gg <- curve_table(data = y[[1]], format = "image"))
```
-Let’s look at our output.
+More bootstrap replications will lead to a smoother function. But for now, we can compare these two functions to see how similar they are.
-```r
-res
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+plot_compare(y[[1]], y[[3]])
```
+The densities can also be calculated accurately using the _t_-bootstrap method. Here we use a different dataset to show this
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+library(Lock5Data)
+dataz <- data(CommuteAtlanta)
+func = function(data, index) {
+ x <- as.numeric(unlist(data[1]))
+ y <- as.numeric(unlist(data[2]))
+ return(mean(x[index]) - mean(y[index]))
+}
```
-Fixed-Effects Model (k = 2)
-Test for Heterogeneity:
-Q(df = 1) = 0.61, p-val = 0.44
+Our function is a simple mean difference. This time, we'll set the method to "t" for the _t_-bootstrap method
-Model Results:
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+z <- curve_boot(data = CommuteAtlanta, func = func, method = "t", replicates = 2000, steps = 1000)
+ggcurve(data = z[[1]])
+ggcurve(data = z[[2]], type = "cd")
+```
-estimate se zval pval ci.lb ci.ub
- 0.16 0.22 0.73 0.47 -0.28 0.60
+The consonance curve and density are nearly identical. With more bootstrap replications, they are very likely to converge.
----
-Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
+```{r echo=TRUE, fig.height=2, fig.width=4}
+(zz <- curve_table(data = z[[1]], format = "image"))
```
-Take a look at the pooled summary effect and its interval. Keep it in
-mind as we move onto constructing a consonance function.
+## Using Profile Likelihoods
-We can now take the object produced by the meta-analysis and calculate a
-P-value and S-value function with it to see the full spectrum of effect
-sizes compatible with the test model at every level. We’ll use the
-`curve_meta()` function to do this.
+For this last example, we'll explore the `curve_lik()` function, which can help generate profile likelihood functions, and deviance statistics with the help of the [`ProfileLikelihood`](https://cran.r-project.org/package=ProfileLikelihood) package.
-``` r
-metaf <- curve_meta(res)
-tibble::tibble(metaf)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+library(ProfileLikelihood)
```
-Now that we have our dataframe with every computed interval, we can plot
-the functions.
+We'll use a simple example taken directly from the [`ProfileLikelihood`](https://cran.r-project.org/package=ProfileLikelihood) documentation where we'll calculate the likelihoods from a glm model
-``` r
-ggconcurve(type = "consonance", metaf)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+data(dataglm)
+xx <- profilelike.glm(y ~ x1 + x2, data=dataglm, profile.theta="group",
+family=binomial(link="logit"), length=500, round=2)
```
-
-
-
+and the consonance functions
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+(plot_compare(
+ data1 = curve1[[1]], data2 = curve2[[1]], type = "c", measure = "ratio", nullvalue = TRUE, title = "Brown et al. 2017. J Clin Psychiatry. vs. \nBrown et al. 2017. JAMA.",
+ subtitle = "J Clin Psychiatry: OR = 1.7, 1/6.83 LI: LL = 1.1, UL = 2.6 \nJAMA: HR = 1.61, 1/6.83 LI: LL = 0.997, UL = 2.59", xaxis = expression(Theta ~ "= Hazard Ratio / Odds Ratio")
+))
+```
-We’ve used a relatively easy example for this blog post, but the
-[**concurve**](https://github.com/Zadchow/concurve)
-package is also able to calculate consonance functions for multiple
-regressions, logistic regressions, ANOVAs, and meta-analyses (that have
-been produced by the ***metafor*** package).
+# The Bootstrap and Consonance Functions
-## Using Meta-Analysis Data
+Some authors have shown that the bootstrap distribution is equal to the confidence distribution because it meets the definition of a consonance distribution.[@efron1994; @efron2018; @xie2013isr] The bootstrap distribution and the asymptotic consonance distribution would be defined as:
-Here we present another quick example with a meta-analysis of simulated
-data.
+$$H_{n}(\theta)=1-P\left(\hat{\theta}-\hat{\theta}^{*} \leq \hat{\theta}-\theta | \mathbf{x}\right)=P\left(\hat{\theta}^{*} \leq \theta | \mathbf{x}\right)$$
-First, we generate random data for two groups in two hypothetical
-studies
+Certain bootstrap methods such as the BCa method and _t_-bootstrap method also yield second order accuracy of consonance distributions.
-``` r
-GroupAData <- runif(20, min = 0, max = 100)
-GroupAMean <- round(mean(GroupAData), digits = 2)
-GroupASD <- round(sd(GroupAData), digits = 2)
+$$H_{n}(\theta)=1-P\left(\frac{\hat{\theta}^{*}-\hat{\theta}}{\widehat{S E}^{*}\left(\hat{\theta}^{*}\right)} \leq \frac{\hat{\theta}-\theta}{\widehat{S E}(\hat{\theta})} | \mathbf{x}\right)$$
-GroupBData <- runif(20, min = 0, max = 100)
-GroupBMean <- round(mean(GroupBData), digits = 2)
-GroupBSD <- round(sd(GroupBData), digits = 2)
+Here, I demonstrate how to use these particular bootstrap methods to arrive at consonance curves and densities.
-GroupCData <- runif(20, min = 0, max = 100)
-GroupCMean <- round(mean(GroupCData), digits = 2)
-GroupCSD <- round(sd(GroupCData), digits = 2)
+We'll use the Iris dataset and construct a function that'll yield a parameter of interest.
-GroupDData <- runif(20, min = 0, max = 100)
-GroupDMean <- round(mean(GroupDData), digits = 2)
-GroupDSD <- round(sd(GroupDData), digits = 2)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+iris <- datasets::iris
+foo <- function(data, indices) {
+ dt <- data[indices, ]
+ c(
+ cor(dt[, 1], dt[, 2], method = "p")
+ )
+}
```
-We can then quickly combine the data in a dataframe.
-
-``` r
-StudyName <- c("Study1", "Study2")
-MeanTreatment <- c(GroupAMean, GroupCMean)
-MeanControl <- c(GroupBMean, GroupDMean)
-SDTreatment <- c(GroupASD, GroupCSD)
-SDControl <- c(GroupBSD, GroupDSD)
-NTreatment <- c(20, 20)
-NControl <- c(20, 20)
-
-metadf <- data.frame(
- StudyName, MeanTreatment, MeanControl,
- SDTreatment, SDControl,
- NTreatment, NControl
-)
+We can now use the `curve_boot()` method to construct a function. The default method used for this function is the "BCa" method provided by the [`bcaboot`](https://cran.r-project.org/package=bcaboot) package.[@efron2018]
+
+```{r include=FALSE}
+y <- curve_boot(data = iris, func = foo, method = "bca", replicates = 2000, steps = 1000)
```
-Then, we’ll use ***metafor*** to calculate the standardized mean
-difference.
+I will suppress the output of the function because it is unnecessarily long. But we've placed all the estimates into a list object called y.
-``` r
-dat <- escalc(
- measure = "SMD",
- m1i = MeanTreatment, sd1i = SDTreatment, n1i = NTreatment,
- m2i = MeanControl, sd2i = SDControl, n2i = NControl,
- data = metadf
-)
+The first item in the list will be the consonance distribution constructed by typical means, while the third item will be the bootstrap approximation to the consonance distribution.
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+ggcurve(data = y[[1]])
+ggcurve(data = y[[3]])
```
-Next, we’ll pool the data using a ~~fixed-effects~~ common-effects model
+We can also print out a table for TeX documents
-``` r
-res <- rma(yi, vi,
- data = dat, slab = paste(StudyName, sep = ", "),
- method = "FE", digits = 2
-)
+```{r echo=TRUE, fig.height=2, fig.width=4}
+(gg <- curve_table(data = y[[1]], format = "image"))
```
-Let’s look at our output.
+More bootstrap replications will lead to a smoother function. But for now, we can compare these two functions to see how similar they are.
-```r
-res
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+plot_compare(y[[1]], y[[3]])
```
+The densities can also be calculated accurately using the _t_-bootstrap method. Here we use a different dataset to show this
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+library(Lock5Data)
+dataz <- data(CommuteAtlanta)
+func = function(data, index) {
+ x <- as.numeric(unlist(data[1]))
+ y <- as.numeric(unlist(data[2]))
+ return(mean(x[index]) - mean(y[index]))
+}
```
-Fixed-Effects Model (k = 2)
-Test for Heterogeneity:
-Q(df = 1) = 0.61, p-val = 0.44
+Our function is a simple mean difference. This time, we'll set the method to "t" for the _t_-bootstrap method
-Model Results:
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+z <- curve_boot(data = CommuteAtlanta, func = func, method = "t", replicates = 2000, steps = 1000)
+ggcurve(data = z[[1]])
+ggcurve(data = z[[2]], type = "cd")
+```
-estimate se zval pval ci.lb ci.ub
- 0.16 0.22 0.73 0.47 -0.28 0.60
+The consonance curve and density are nearly identical. With more bootstrap replications, they are very likely to converge.
----
-Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
+```{r echo=TRUE, fig.height=2, fig.width=4}
+(zz <- curve_table(data = z[[1]], format = "image"))
```
-Take a look at the pooled summary effect and its interval. Keep it in
-mind as we move onto constructing a consonance function.
+## Using Profile Likelihoods
-We can now take the object produced by the meta-analysis and calculate a
-P-value and S-value function with it to see the full spectrum of effect
-sizes compatible with the test model at every level. We’ll use the
-`curve_meta()` function to do this.
+For this last example, we'll explore the `curve_lik()` function, which can help generate profile likelihood functions, and deviance statistics with the help of the [`ProfileLikelihood`](https://cran.r-project.org/package=ProfileLikelihood) package.
-``` r
-metaf <- curve_meta(res)
-tibble::tibble(metaf)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+library(ProfileLikelihood)
```
-Now that we have our dataframe with every computed interval, we can plot
-the functions.
+We'll use a simple example taken directly from the [`ProfileLikelihood`](https://cran.r-project.org/package=ProfileLikelihood) documentation where we'll calculate the likelihoods from a glm model
-``` r
-ggconcurve(type = "consonance", metaf)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+data(dataglm)
+xx <- profilelike.glm(y ~ x1 + x2, data=dataglm, profile.theta="group",
+family=binomial(link="logit"), length=500, round=2)
```
-
- -
+Then, we’ll use `curve_lik()` on the object that the [`ProfileLikelihood`](https://cran.r-project.org/package=ProfileLikelihood) package created.
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+lik <- curve_lik(xx, dataglm)
+tibble::tibble(lik[[1]])
+```
-And our S-value function
+Next, we’ll plot three functions, the relative likelihood, the log likelihood, the likelihoodm, and the deviance function.
-``` r
-ggconcurve(type = "surprisal", metaf)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+ggcurve(lik[[1]], type = "l1")
+ggcurve(lik[[1]], type = "l2")
+ggcurve(lik[[1]], type = "l3")
+ggcurve(lik[[1]], type = "d")
```
-
-
-
+Then, we’ll use `curve_lik()` on the object that the [`ProfileLikelihood`](https://cran.r-project.org/package=ProfileLikelihood) package created.
+
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+lik <- curve_lik(xx, dataglm)
+tibble::tibble(lik[[1]])
+```
-And our S-value function
+Next, we’ll plot three functions, the relative likelihood, the log likelihood, the likelihoodm, and the deviance function.
-``` r
-ggconcurve(type = "surprisal", metaf)
+```{r echo=TRUE, fig.height=4.5, fig.width=6}
+ggcurve(lik[[1]], type = "l1")
+ggcurve(lik[[1]], type = "l2")
+ggcurve(lik[[1]], type = "l3")
+ggcurve(lik[[1]], type = "d")
```
-
- -
-
-Compare the span of these functions and the information they provide to
-the consonance interval provided by the forest plot. We are now no
-longer limited to interpreting an arbitrarily chosen interval by
-mindless analytic decisions often built into statistical packages by
-default.
+
+The obvious advantage of using reduced likelihoods is that they are free of nuisance parameters
+
+$$L_{t_{n}}(\theta)=f_{n}\left(F_{n}^{-1}\left(H_{p i v}(\theta)\right)\right)\left|\frac{\partial}{\partial t} \psi\left(t_{n}, \theta\right)\right|=h_{p i v}(\theta)\left|\frac{\partial}{\partial t} \psi(t, \theta)\right| /\left.\left|\frac{\partial}{\partial \theta} \psi(t, \theta)\right|\right|_{t=t_{n}}$$
+thus, giving summaries of the data that can be incorporated into combined analyses.
+
+* * *
+
+# References
+
+* * *
diff --git a/vignettes/examples.html b/vignettes/examples.html
deleted file mode 100644
index a792cdb..0000000
--- a/vignettes/examples.html
+++ /dev/null
@@ -1,484 +0,0 @@
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-Examples in R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-Compare the span of these functions and the information they provide to
-the consonance interval provided by the forest plot. We are now no
-longer limited to interpreting an arbitrarily chosen interval by
-mindless analytic decisions often built into statistical packages by
-default.
+
+The obvious advantage of using reduced likelihoods is that they are free of nuisance parameters
+
+$$L_{t_{n}}(\theta)=f_{n}\left(F_{n}^{-1}\left(H_{p i v}(\theta)\right)\right)\left|\frac{\partial}{\partial t} \psi\left(t_{n}, \theta\right)\right|=h_{p i v}(\theta)\left|\frac{\partial}{\partial t} \psi(t, \theta)\right| /\left.\left|\frac{\partial}{\partial \theta} \psi(t, \theta)\right|\right|_{t=t_{n}}$$
+thus, giving summaries of the data that can be incorporated into combined analyses.
+
+* * *
+
+# References
+
+* * *
diff --git a/vignettes/examples.html b/vignettes/examples.html
deleted file mode 100644
index a792cdb..0000000
--- a/vignettes/examples.html
+++ /dev/null
@@ -1,484 +0,0 @@
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-Examples in R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-Examples in R
-
-
-
-
-
Using Mean Differences
-
If we were to generate some random data from a normal distribution with the following code,
-
-
and compare the means of these two “groups” using a t-test,
-
-
we would likely see some differences, given that we have such a small sample in each group.
-
-
We can see our P-value for the statistical test along with the computed 95% interval with the command above (which is given to us by default by the program). Thus, effect sizes that range from the lower bound of this interval to the upper bound are compatible with the test model at this consonance level.
-
However, as stated before, a 95% interval is only an artifact of the commonly used 5% alpha level for hypothesis testing and is nowhere near as informative as a function.
-
If we were to take the information from this data and calculate a P-value function where every single consonance interval and its corresponding P-value were plotted, we would be able to see the full range of effect sizes compatible with the test model at various levels.
-
It is relatively easy to produce such a function using the concurve package in R.
-
Install the package directly from CRAN
-
-
or get a more slightly up-to-date version via GitHub.
-
-
We’ll use the same data from above to calculate a P-value function and since we are focusing on mean differences using a t-test, we will use the curve_meta() function to calculate our consonance intervals and store them in a dataframe.
-
-
Now thousands of consonance intervals at various levels have been stored in the dataframe “intervalsdf.” We can preview some of the entries via the tibble package.
-
-
There’s a quick look at the first few entries of our dataframe.
-
We can plot this data using the ggconcurve() function.
-
-
- -
-
-
Now we can see every consonance interval and its corresponding P-value and consonance level plotted. As stated before, a single 95% consonance interval is simply a slice through this function, which provides far more information as to what is compatible with the test model and its assumptions.
-
Furthermore, we can also produce a “surprisal” function by plotting every consonance interval and its corresponding S-value using the ggconcurve() function with type being set as “surprisal”.
-
-
- -
-
-
The graph from the code above provides us with consonance levels and the maximum amount of information against the effect sizes contained in the consonance interval.
-
-
Simple Linear Models
-
We can also try this with other simple linear models.
-
Let’s simulate more normal data and fit a simple linear regression to it using ordinary least squares regression with the base R lm() function.
-
-
We can see some of the basic statistics of our model including the 95% interval for our predictor (GroupB). Perhaps we want more information. Well we can do that! Using the curve_gen(), we can calculate several consonance intervals for the regression coefficient and then plot the consonance and surprisal functions.
-
-
Now that we have our data frame, we can graph our function.
-
-
- -
-
-
-
- -
-
-
We can also compare these functions to likelihood functions (also called support intervals), and we’ll see that we get very similar results. We’ll do this using the ProfileLikelihood package.
-
-
Now we plot our likelihood function and we can see what the maximum likelihood estimation is. Notice that it’s practically similar to the interval in the S-value function with 0 bits of information against it and and the consonance interval in the P-value function with a P-value of 1.
-
-
- -
-
-
We’ve used a relatively easy example for this blog post, but the concurve package is also able to calculate consonance functions for multiple regressions, logistic regressions, ANOVAs, and meta-analyses (that have been produced by the metafor package).
-
-
Using Meta-Analysis Data
-
Here we present another quick example with a meta-analysis of simulated data.
-
First, we generate random data for two groups in two hypothetical studies
-
GroupAData <- runif(20, min = 0, max = 100)
-GroupAMean <- round(mean(GroupAData), digits = 2)
-GroupASD <- round(sd(GroupAData), digits = 2)
-
-GroupBData <- runif(20, min = 0, max = 100)
-GroupBMean <- round(mean(GroupBData), digits = 2)
-GroupBSD <- round(sd(GroupBData), digits = 2)
-
-GroupCData <- runif(20, min = 0, max = 100)
-GroupCMean <- round(mean(GroupCData), digits = 2)
-GroupCSD <- round(sd(GroupCData), digits = 2)
-
-GroupDData <- runif(20, min = 0, max = 100)
-GroupDMean <- round(mean(GroupDData), digits = 2)
-GroupDSD <- round(sd(GroupDData), digits = 2)
-
We can then quickly combine the data in a dataframe.
-
StudyName <- c("Study1", "Study2")
-MeanTreatment <- c(GroupAMean, GroupCMean)
-MeanControl <- c(GroupBMean, GroupDMean)
-SDTreatment <- c(GroupASD, GroupCSD)
-SDControl <- c(GroupBSD, GroupDSD)
-NTreatment <- c(20, 20)
-NControl <- c(20, 20)
-
-metadf <- data.frame(
- StudyName, MeanTreatment, MeanControl,
- SDTreatment, SDControl,
- NTreatment, NControl
-)
-
Then, we’ll use metafor to calculate the standardized mean difference.
-
-
Next, we’ll pool the data using a fixed-effects common-effects model
-
-
Let’s look at our output.
-
-
Fixed-Effects Model (k = 2)
-
-Test for Heterogeneity:
-Q(df = 1) = 0.61, p-val = 0.44
-
-Model Results:
-
-estimate se zval pval ci.lb ci.ub
- 0.16 0.22 0.73 0.47 -0.28 0.60
-
----
-Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
-
Take a look at the pooled summary effect and its interval. Keep it in mind as we move onto constructing a consonance function.
-
We can now take the object produced by the meta-analysis and calculate a P-value and S-value function with it to see the full spectrum of effect sizes compatible with the test model at every level. We’ll use the curve_meta() function to do this.
-
-
Now that we have our dataframe with every computed interval, we can plot the functions.
-
-
- -
-
-
And our S-value function
-
-
- -
-
-
Compare the span of these functions and the information they provide to the consonance interval provided by the forest plot. We are now no longer limited to interpreting an arbitrarily chosen interval by mindless analytic decisions often built into statistical packages by default.
-
Using Stata
-
-
-
-Although concurve was originally designed to be used in R, it is possible to achieve very similar results in Stata. We can use some datasets that are built into Stata to show how to achieve this.
-First, let’s load the auto2 dataset which contains data about cars and their characteristics.
-
-Browse the dataset in your databrowser to get more familiar with some of the variables. Let’s say we’re interested in the relationship between miles per gallon and price. We could fit a very simple linear model to assess that relationship.
-First, let’s visualize the data with a scatterplot.
-
-
-
- -
-
-
-
That’s what our data looks like. Clearly there seems to be an inverse relationship between miles per gallon and price.
-Now we could fit a very simple linear model with miles per gallon being the predictor and price being the outcome and get some estimates of the relationship.
-
-
-
- -
-
-
-
That’s what our output looks like.
-Our output also gives us 95% consonance (confidence) intervals by default. The interval includes values as low as -344 and as high as -133. Here’s what our model looks graphed.
-
-
- -
-
-
-
-Unfortunately, the program only gives us one interval at 95% and we’re interested in seeing every single interval at every level, and plotting it to form a function.
-Here’s the code that we’ll be using to achieve that.
-
-That’s a lot and may seem intimidating at first, but I’ll explain it line by line.
-
-“postfile” is the command that will be responsible for pasting the data from our overall loop into a new dataset. Here, we are telling Stata that the internal Stata memory used to hold these results (the post) will be named “topost” and that it will have five variables, “level”, “pvalue”, “svalue”, “lointerval”, and “upinterval.”
-
-“level” will contain the consonance level that corresponds to the limits of the interval, with “lointerval” being the lower bound of the interval and “upinterval” being the upper bound.
“pvalue”is computed by taking 1 - “level”, which is alpha.
“svalue”is computed by taking the \(-log_{2}\) of the computed P-value, and this column will be used to plot the surprisal function.
“my_new_data” is the filename that we’ve assigned to our new dataset.
“replace” indicates that if there is an existing filename that already exists, we’re willing to relace it.
-Here are the next few major lines
-
-The command “forvalues” is responsible for taking a set of numbers that we provide it, and running the contents within the braces through those numbers. So here, we’ve set the local macro “i” to contain numbers between 10 and 99.99 for our consonance levels. Why 10? Stata cannot compute consonance intervals lower than 10%.
-Our next line contains the actual contents of what we want to do. Here, it says that we will run a simple linear regression where mpg is the predictor and where price is the outcome, and that the outputs for each loop will be suppressed, hence the “quiet.”
-Then, we have the command “level” with the local macro “i” inside of it. As you may already know, “level” dictates the consonance level that Stata provides us. By default, this is set to 95%, but here, we’ve set it “i”, which we established via “forvalues” as being set to numbers between 10 and 99.
-The next line two lines
-
-indicate that we will take variables of a certain class r(), (this class contains the interval bounds we need) and place them within a matrix called E. Then we will list the contents of this matrix.
-
-From the contents of this matrix list, we will take the estimates from the fifth and sixth rows (look at the last two paranthesis of this line of code above and then the image below) in the first column which contain our consonance limits, with the fifth row containing the lower bound of the interval and the sixth containing the upper bound.
-
-
- -
-
-
-
-We will place the contents from the fifth row into the second variable we set originally for our new dataset, which was “lointerval.” The contents of the sixth row will be placed into “upinterval.”
-All potential values of “i” (10-99) will be placed into the first variable that we set, “level”. From this first variable, we can compute the second variable we set up, which was “Pvalue” and we’ve done that here by subtracting “level” from 1 and then dividing the whole equation by 100, so that our P-value can be on the proper scale. Our third variable, which is the longest, computes the “Svalue” by using the previous variable, the “Pvalue” and taking the \(-log_{2}\) of it.
-The relationships between the variables on this line and the variables we set up in the very first line are dictated by the order of the commands we have set, and therefore they correspond to the same order.
-“post topost” is writing the results from each loop as new observations in this data structure.
-With that, our loop has concluded, and we can now tell Stata that “post” is no longer needed
-
-We then tell Stata to clear its memory to make room for the new dataset we just created and we can list the contents of this new dataset.
-
-Now we have an actual dataset with all the consonance intervals at all the levels we wanted, ranging from 10% all the way up to 99%.
-In order to get a function, we’ll need to be able to graph these results, and that can be tricky since for each observation we have one y value (the consonance level), and two x values, the lower bound of the interval and the upper bound of the interval.
-So a typical scatterplot will not work, since Stata will only accept one x value. To bypass this, we’ll have to use a paired-coordinate scatterplot which will allow us to plot two different y variables and two different x variables.
-Of course, we don’t need two y variables, so we can set both options to the variable “level”, and then we can set our first x variable to “lointerval” and the second x variable to “upinterval.”
-This can all be done with the following commands, which will also allow us to set the title and subtitle of the graph, along with the titles of the axes.
-
-However, I would recommend using the menu to customize the plots as much as possible. Simply go to the Graphics menu and select Twoway Graphs. Then create a new plot definition, and select the Advanced plots and choose a paired coordinate scatterplot and fill in the y variables, both of which will be “levels” and the x variables, which will be “lointerval” and “upinterval”.
-
-
- -
-
-
-
-So now, here’s what our consonance function looks like.
-
-
- -
-
-
-
And here’s what our surprisal function looks like.
-
-
- -
-
-
-
It looks slighly better when the y-axis is transformed logarithmically…
-
-
- -
-
-
-
…but then we lose our ability to differentiate between the effects contained in intervals with higher bits of information and S-values are already logarithmically scaled.
-It’s clear that in both plots, we’re missing values of intervals with a consonance level of less than 10%, but unfortunately, this is the best Stata can do, and what we’ll have to work with. It may not look as pretty as an output from R, but it’s far more useful than blankly staring at a 95% interval and thinking that it is the only piece of information we have regarding compatibility of different effect estimates.
-The code that I have pasted above can be used for most commands in Stata that have an option to calculate a consonance level. Thus, if there’s an option for “level”, then the commands above will work to produce a dataset of several consonance intervals.
-For example, if we wished to fit a generalized linear model, here’s what our code would look like.
-
-We simply replace the first line within the loop with our intended command, just as I’ve replaced
-
-with
-
-If we wanted fit something more complex, like a multilevel mixed model that used restricted maximum likelihood, here’s what our code would look like
-
-Basically, our code doesn’t really change that much and with only a few lines of it, we are able to produce graphical tools that can better help us interpret the wide range of effect sizes that are compatible with the model and its assumptions.
-
-
-
-
-
-
-
-
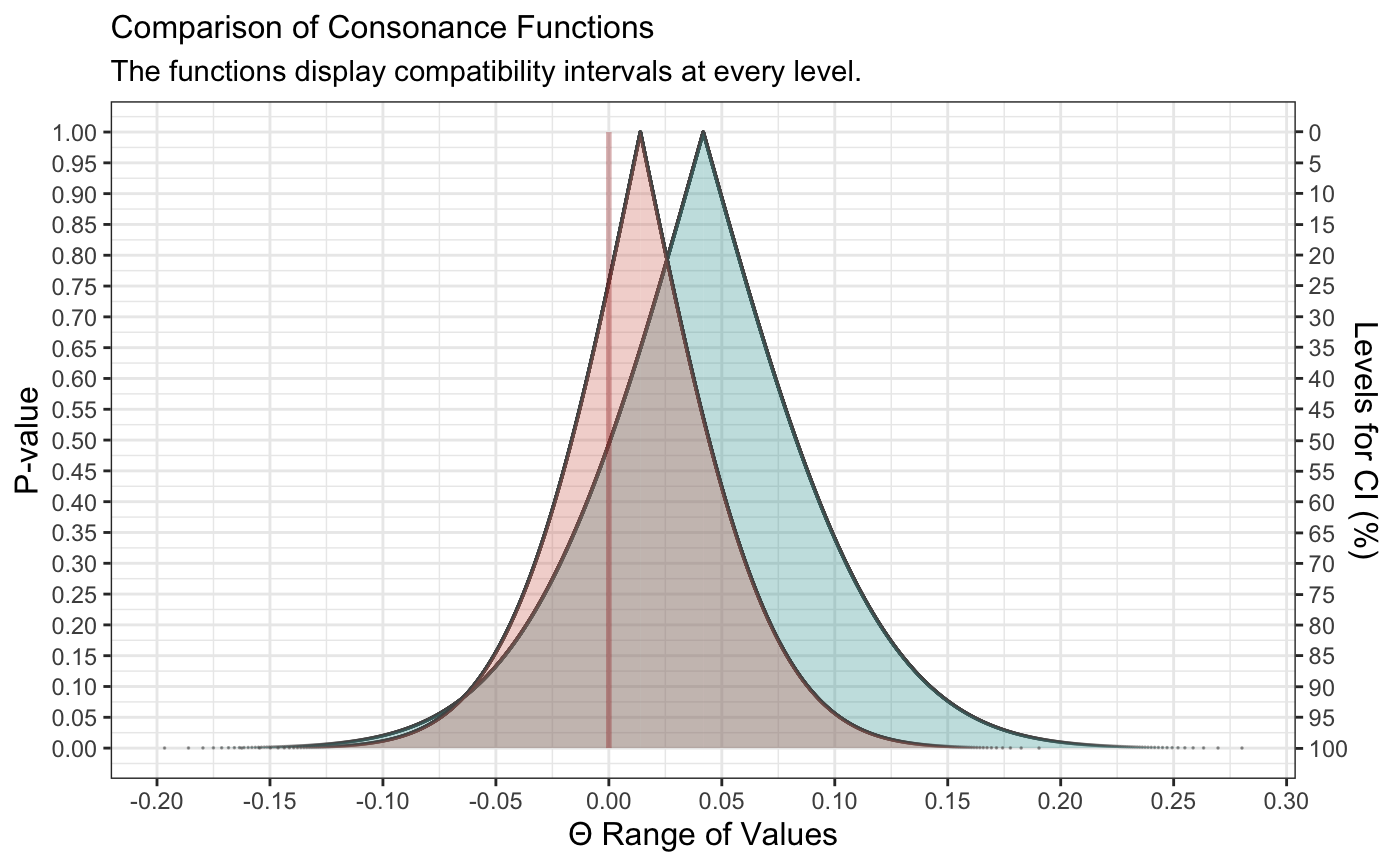 +
+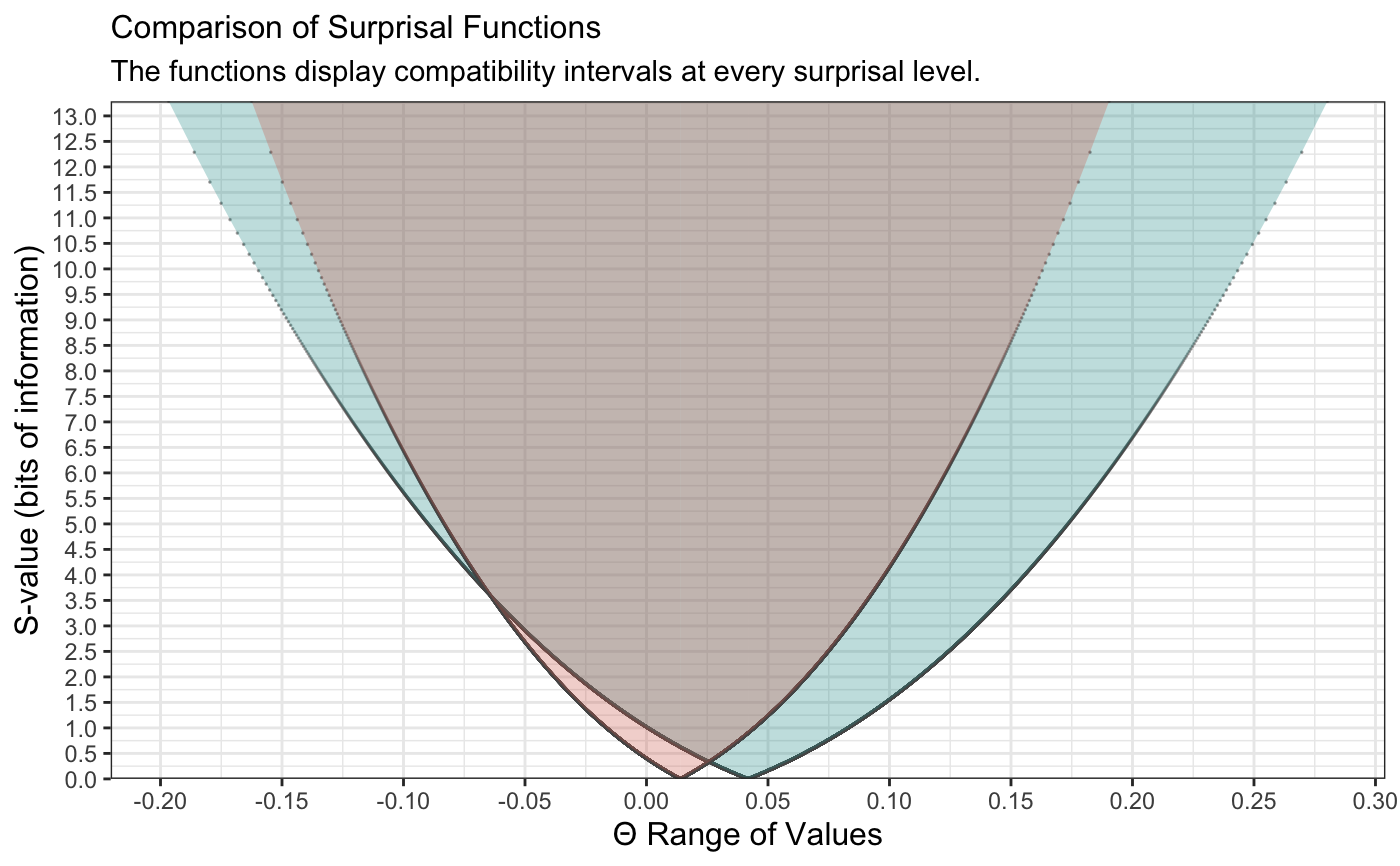 +
+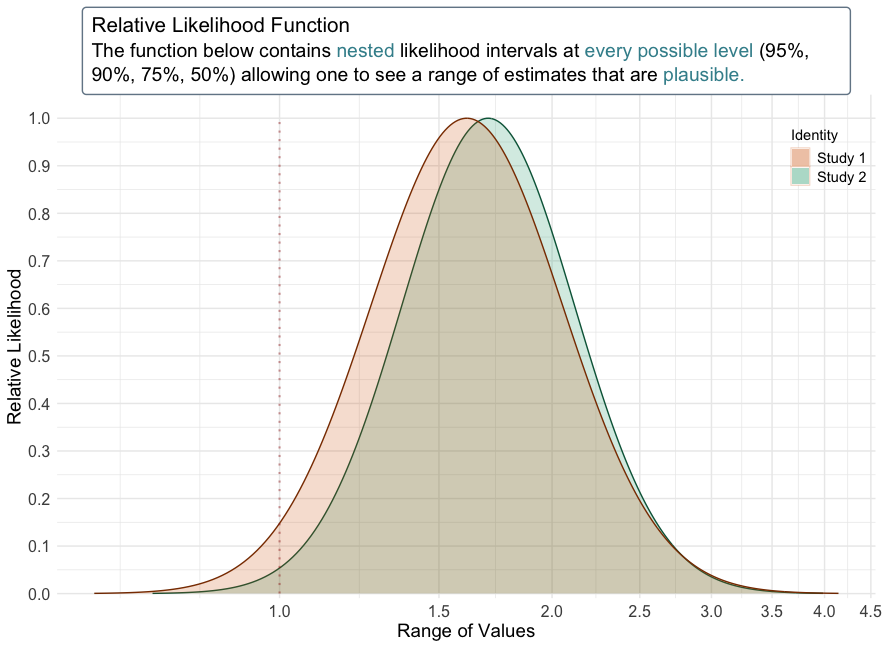 +
+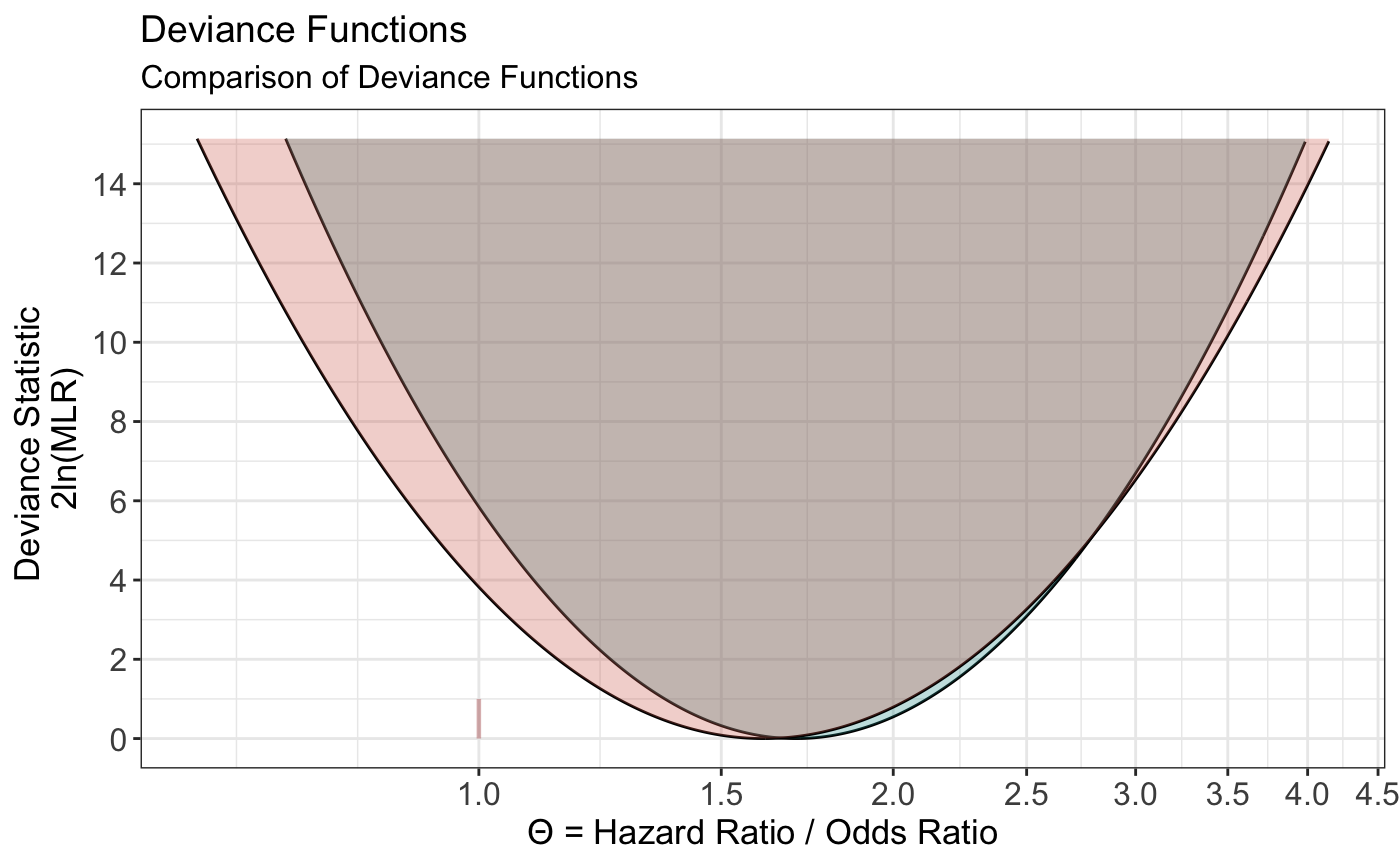 -
- -
- +* * *
-* * *
+### [Export Tables](file:///Users/Zad/Desktop/GitHub/concurve/docs/reference/curve_table.html) Easily For Word, Powerpoint, & TeX documents
+
+* * *
-* * *
+### [Export Tables](file:///Users/Zad/Desktop/GitHub/concurve/docs/reference/curve_table.html) Easily For Word, Powerpoint, & TeX documents
+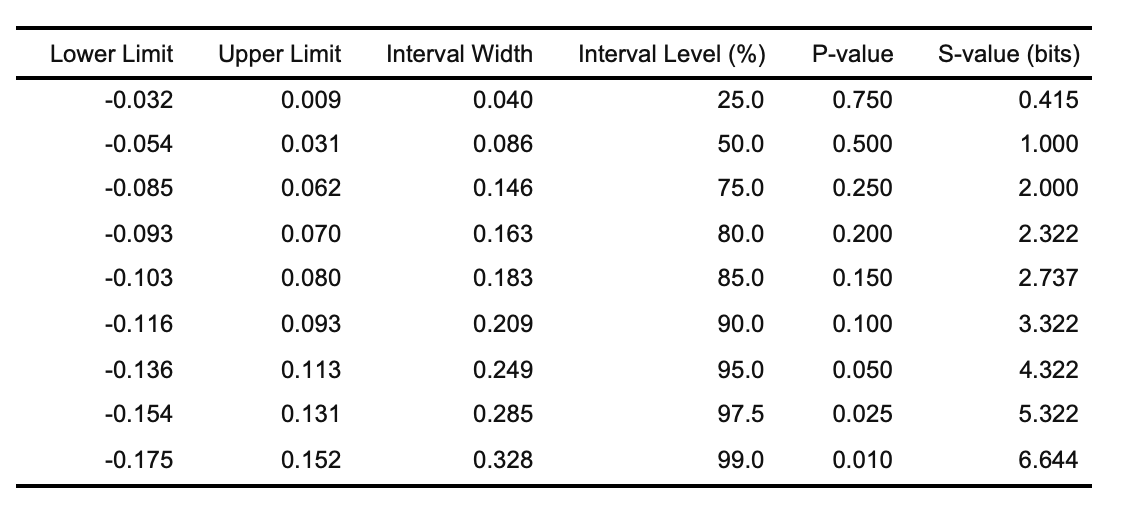 -# Installation
+
-# Installation
+ +
+ -
- +
+ +
+ +
+ +
+ -----
-# Installation
+### [Export Tables](file:///Users/Zad/Desktop/GitHub/concurve/docs/reference/curve_table.html) Easily For Word, Powerpoint, & TeX documents
-## For R:
+
-----
-# Installation
+### [Export Tables](file:///Users/Zad/Desktop/GitHub/concurve/docs/reference/curve_table.html) Easily For Word, Powerpoint, & TeX documents
-## For R:
+ -``` r
-install.packages("concurve")
-```
+
-``` r
-install.packages("concurve")
-```
+ -### Install the Developer Version
+
-### Install the Developer Version
+ -
- -
- -
- -
- -
-

















 -
- -
-















