Network evolution

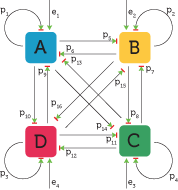
Biological gene regulation can be modeled using abstract networks called gene regulatory networks (GRNs). There are often a large number of complex interactions between genetic components in a living cell, however they can be simplified into network models by looking at the overall effect of one gene on another, whether it is positive (activation) or negative (repression), and the strength of the interaction (giving the response curve). These simple networks, although being far from the complex, and essentially random environment found in living cells, can give rise to functional behaviours which we see in living systems. A notable example is the biological clock network. Many organisms have evolved a natural rhythm (the circadian rhythm) which allows them to anticipate environmental changes over a 24 hour period. The GRN underpinning the clock has been resolved, and we are able to understand how organisms perform this essential function at the genetic level.

Aims

Methods

1. Structure of modular code base

• Network constructor module
  • contains all methods for creating networks
  • currently set to BoolNetwork
  • could switch this to be more complex discrete/continuous system
• Network simulation module
  • runs a dynamic network simulation for one generation
  • currently set to BoolSim
  • could switch to difference/ODE/DDE/SDDE system
• Evolution module
  • defines the processes of recombination, crossover, mutation
  • defines the fitness function
  • currently set to EvolveClock
  • could switch to EvolveBetHedging
• Genetic Algorithm module
  • pulls all modules together and runs the GA over multiple generations
• Parameters module
  • sets all parameters that are not specific to the system (e.g. number of nodes)
  • creates hash that can be passed around from module to module
• Running script
  • adds system specific parameters (e.g. day/night cycle for clock)
  • set out which modules should be taken in by the GA module
  • sets outputs (profiling/plots/network cartoon)
  • currently set to runboolclock

The following sections refer to the current setup (boolean simulation and clock evolution).

2. Boolean network representation (BoolNetwork)

Paths

• Activation: 1
• Repression: -1
• No interaction: 0
• Stochastic activation/repression:
  • Markov chain of 0s and 1/-1s
  • evolvable transition matrix

Gates

• 'and'
  • to turn an on(off) gene off(on):
    • all paths that are repression(activation) must be active (i.e. origin gene must be on)
    • the number of incoming repressions(activations) must exceed that of incoming activations(repressions)
• 'or'
  • to turn an on(off) gene off(on):
    • the number of active incoming repressions(activations) must be greater than (or equal to) the number of incoming active activations(repressions)

Lags

currently there is no minimum, maybe there should be

Environmental signal and response

• The environmental signal is a chain of 0s and 1s which indicate, for each minute of the simulation, whether or not there is an environmental signal
• The environmental paths are set for each gene as either 0 (can't detect the environmental signal) or 1 (activated by environmental signal)
• Maybe the environmental response should have a lag too
• Maybe the environment should also be able to repress genes

3. Dynamic boolean simulation (BoolSim)

• initially all genes are on
• if there are no incoming paths a gene will switch/stay on
• system updates every minute according to gates and incoming paths
• first a decision hash is constructed
  • the keys are all the possible combinations of all genes/paths/gates (multichoose)
  • for each key, the value shows the value of the gene of interest at time t + 1

Example for just one incoming gene (so no gate required):

gene 1	path 1	time t		time t+1
0	0	0	=>	1
1	0	0	=>	1
0	1	0	=>	1
1	1	0	=>	1
0	-1	0	=>	1
1	-1	0	=>	0
0	0	1	=>	1
1	0	1	=>	1
0	1	1	=>	1
1	1	1	=>	1
0	-1	1	=>	1
1	-1	1	=>	0

This hash only needs to be made once since it contains all possible combinations. Then for each minute, for each gene $g_{i}$, an array capturing the state of all incoming interactions is constructed (termed the decision array), and is compared to the keys. The value of $g_{i}$ at the subsequent time point is set as the value of the matched key in the decision hash.

To make the decision array:

• take the value of each gene and each path at time $t - lag_{i}$
• take the value of the gate
• take the value of each environmental path
• take the value of the environmental input

4. Evolution

Mutation

• paths can be mutated to have a different sign
  • 0 => 1
  • 0 => -1
  • 1 => -1
  • -1 => 1
• transition matrices can be mutated according to a truncated [0, 1] normal distribution around the mean (current) level (for clock evo all transition matrices are set to [1, 0; 0, 1])
• lags can be mutated according to a truncated [0, maxlag] normal distribution around the mean (current) lag (currently the standard deviation is low and mutation rate is high)
• gates are mutated or/and => and/or
• environmental paths 1/0 => 0/1

Recombination

• Parental pairs are selected from the population probabilistically with a scaled exponential distribution such that fitness correlates with likelihood of selection.
• each pair will produce one offspring consisting of a random combination of features from each parent
• the number of pairs is equal to the killing threshold (percentage of population killed each generation) so that the population remains the same size throughout evolutionary time

Survival

Currently the least fit 15% of the population will be killed each generation.