Almetro Library

version number: 1.0.7 author: Arnour Sabino

Overview

A python library to measure algorithms execution time and compare with its theoretical complexity.

Installation / Usage

To install use pip:

$ pip install almetro

Or clone the repo:

$ git clone https://github.com/arnour/almetro.git
$ python setup.py install

Information

Almetro uses timeit module from python to time your algorithms.

See more here

Examples

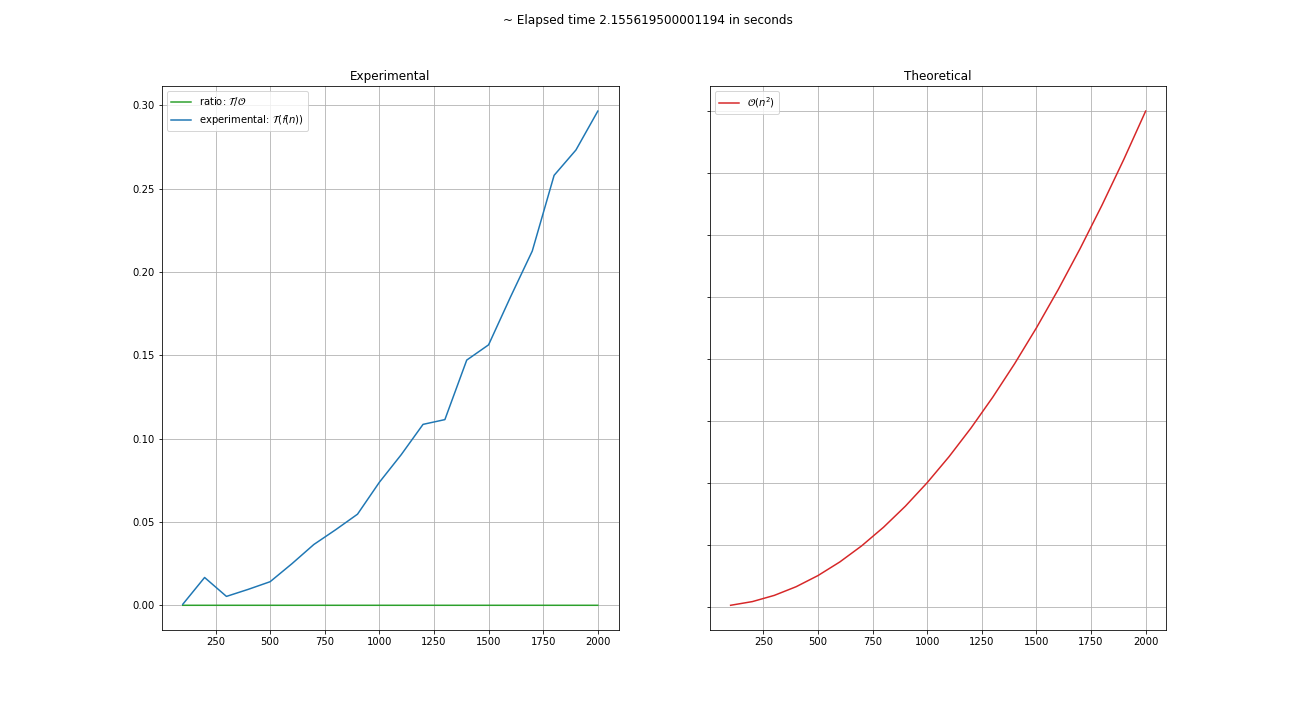
Applying Almetro to a quadratic algorithm:

import almetro
from almetro.algorithms import loop_n_quadratic
from almetro.complexity import cn_quadratic
from almetro.instance import growing

metro = almetro\
            .new()\
            .with_execution(trials=5)\
            .with_instances(instances=20, provider=growing(initial_size=100, growth_size=100))\
            .metro(algorithm=loop_n_quadratic, complexity=cn_quadratic)

chart = metro.chart()

chart.show()

---

Applying Almetro to a lg n algorithm:

import almetro
from almetro.algorithms import loop_n_log
from almetro.complexity import clog_n
from almetro.instance import growing

metro = almetro\
            .new()\
            .with_execution(trials=100)\
            .with_instances(instances=20, provider=growing(initial_size=10000, growth_size=10000))\
            .metro(algorithm=loop_n_log, complexity=clog_n)

chart = metro.chart()

chart.show()

---

Customazing execution:

import almetro
from almetro.complexity import Complexity
from almetro.instance import generator

my_custom_complexity = Complexity(
    theoretical=lambda v=1, e=1, c=1: v * v,
    experimental=lambda v=1, e=1, c=1: v + e,
    text='O(v^2)',
    latex=r'$\mathcal{O}(v^2)$'
)

# You need to provide instances as dict: {'name': '', 'size': {}, 'value': {}}
# Size must contains all needed theoretical complexity arguments
# Value must contain all needed algorithms arguments

def my_custom_instances(n):
    g = create_some_graph()
    for _ in range(n):
        yield {
            'name': 'my instance name',
            'size': {'v': len(g.nodes()), 'e': len(g.edges())}, 'c': some_order_value(),
            'value': {
                'graph': g,
                'v': len(g.nodes())
            }
        }

def my_custom_algorithm(graph, v):
    # Do some stuff
    pass

N = 50

instances_generator = my_custom_instances(N)

# Trials determine how many times each instance will be repeated for Almetro to pick the min time. That way you can exclude some noise from your analisys.
metro = almetro\
            .new()\
            .with_execution(trials=5)\
            .with_instances(instances=N, provider=generator(instances_generator)\
            .metro(algorithm=my_custom_algorithm, complexity=my_custom_complexity)

metro.chart().show()

metro.table().show()

---