A modified implementation of temporal walk algorithm from "Continuous-Time Dynamic Network Embeddings" paper.
This project enables the construction of large temporal networks in memory, from which temporal walks can be sampled. Temporal walks are invaluable in graph neural networks (GNNs) for learning network dynamics.
This library facilitates the creation of temporal graphs and the incremental sampling of temporal walks based on the current graph state, making it especially useful for training GNNs. PyBind is interfaced which let's the functions to be called from Python. For convenience the walks are returned as numpy arrays.
The library also supports the creation of continuous graphs with a maximum time capacity, where edges with timestamps older than the current time minus the maximum capacity are automatically deleted.
A temporal network represents a dynamic system where edges or interactions between nodes vary over time. In contrast to static networks, temporal networks capture changes and sequences in connectivity, which is essential in understanding real-world phenomena like social interactions, information spread, and transportation flows over time.
A temporal walk is a path through a temporal network that respects the order of timestamps on edges, ensuring causality. Temporal walks are particularly useful for applications in graph neural networks (GNNs), where learning temporal dependencies enhances the model's ability to predict or understand evolving network structures.
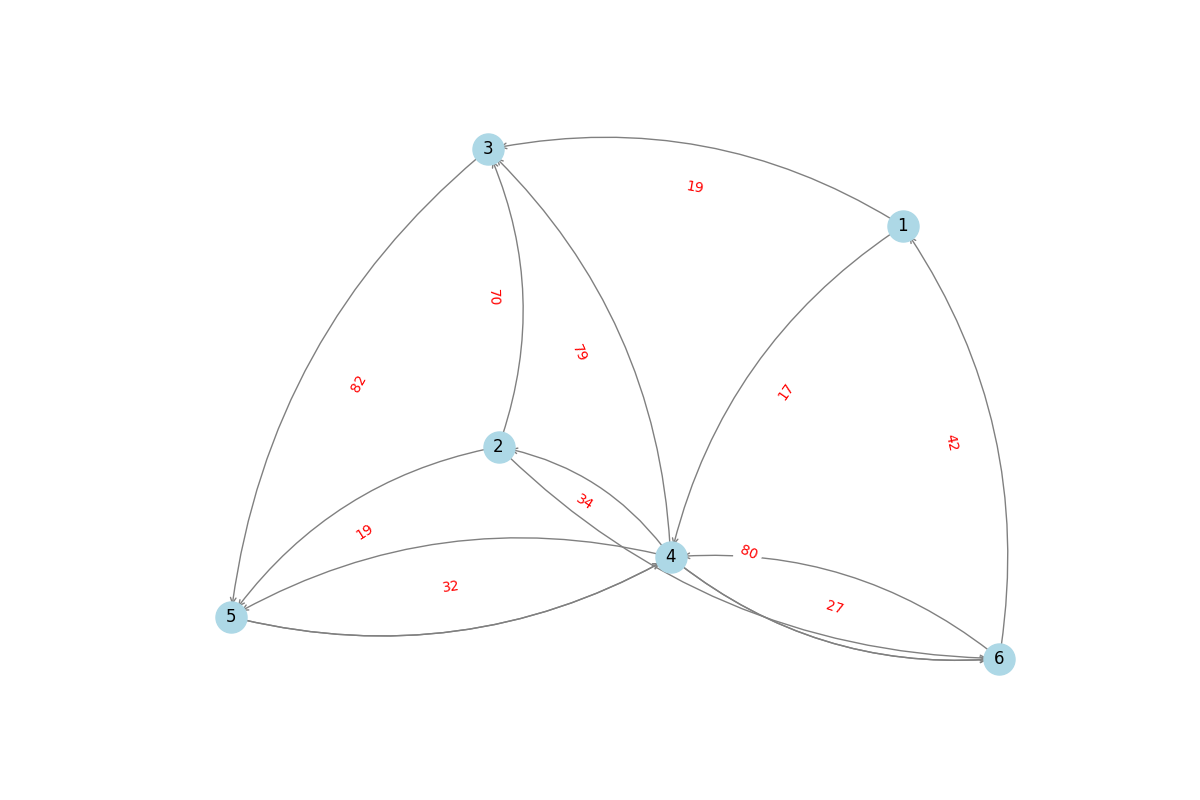
For a given temporal network with following edges (upstream node, downstream node, timestamp),
[
(4, 5, 71),
(3, 5, 82),
(1, 3, 19),
(4, 2, 34),
(4, 3, 79),
(2, 5, 19),
(2, 3, 70),
(5, 4, 97),
(4, 6, 57),
(6, 4, 27),
(2, 6, 80),
(6, 1, 42),
(4, 6, 98),
(1, 4, 17),
(5, 4, 32)
]
Five walks staring at node 2 with linear probability along with their timestamps,
(2, -9223372036854775808), (3, 70), (5, 82), (4, 97), (6, 98)
(2, -9223372036854775808), (5, 19), (4, 32), (5, 71), (4, 97), (6, 98)
(2, -9223372036854775808), (5, 19), (4, 32), (2, 34), (3, 70), (5, 82), (4, 97), (6, 98)
(2, -9223372036854775808), (5, 19), (4, 97), (6, 98)
(2, -9223372036854775808), (3, 70), (5, 82), (4, 97), (6, 98)
Five walks ending at node 2 with linear probability,
(6, 27), (4, 34), (2, 9223372036854775807)
(2, 19), (5, 32), (4, 34), (2, 9223372036854775807)
(6, 27), (4, 34), (2, 9223372036854775807)
(6, 27), (4, 34), (2, 9223372036854775807)
(1, 17), (4, 34), (2, 9223372036854775807)
Five walks staring at node 2 with exponential probability,
(2, -9223372036854775808), (6, 80)
(2, -9223372036854775808), (5, 19), (4, 32), (2, 34), (3, 70), (5, 82), (4, 97), (6, 98)
(2, -9223372036854775808), (5, 19), (4, 32), (2, 34), (6, 80)
(2, -9223372036854775808), (5, 19), (4, 32), (5, 71), (4, 97), (6, 98)
(2, -9223372036854775808), (5, 19), (4, 32), (2, 34), (6, 80)
Five walks ending at node 2 with exponential probability,
(2, 19), (5, 32), (4, 34), (2, 9223372036854775807)
(2, 19), (5, 32), (4, 34), (2, 9223372036854775807)
(6, 27), (4, 34), (2, 9223372036854775807)
(2, 19), (5, 32), (4, 34), (2, 9223372036854775807)
(2, 19), (5, 32), (4, 34), (2, 9223372036854775807)
Five walks staring at node 2 with uniform probability,
(2, -9223372036854775808), (3, 70), (5, 82), (4, 97), (6, 98)
(2, -9223372036854775808), (5, 19), (4, 97), (6, 98)
(2, -9223372036854775808), (5, 19), (4, 97), (6, 98)
(2, -9223372036854775808), (6, 80)
(2, -9223372036854775808), (5, 19), (4, 32), (2, 34), (6, 80)
Five walks ending at node 2 with uniform probability,
(6, 27), (4, 34), (2, 9223372036854775807)
(6, 27), (4, 34), (2, 9223372036854775807)
(2, 19), (5, 32), (4, 34), (2, 9223372036854775807)
(1, 17), (4, 34), (2, 9223372036854775807)
(6, 27), (4, 34), (2, 9223372036854775807)
This project can be installed using pip.
pip install temporal-walkTemporalWalk class contains the public facing functions.
TemporalWalk(int num_walks, int len_walk, RandomPickerType picker_type, int64_t max_time_capacity=-1);Initializes a TemporalWalk object with the specified number of walks, length of each walk, the type of random picker to be used and the maximum time capacity of the graph. Three random pickers are available Exponential, Linear and Uniform. The default value of max_time_capacity is -1, which means unlimited capacity. If set then edges older than max_time_capacity from the latest timestamp are deleted automatically.
void add_multiple_edges(const std::vector<EdgeInfo>& edge_infos);Adds multiple edges to the temporal graph based on the provided vector of EdgeInfo structures, where each structure contains the source node u, destination node i, and timestamp t.
std::vector<std::vector<int>> get_random_walks(WalkStartAt walk_start_at, int end_node=-1);Generates a specified number of random walks from the temporal graph. The walks can be sampled from destination to source or source to destination. This can be controlled using walk_start_at, which can have values Begin, End or Random. An end-node can be specified to start or end the walks. The default value -1 picks the end-node randomly.
std::unordered_map<int, std::vector<std::vector<int>>> get_random_walks_for_nodes(WalkStartAt walk_start_at, const std::vector<int>& end_nodes);Generates random walks for multiple specified nodes in the temporal graph. The walks can be sampled from destination to source or source to destination, controlled by the walk_start_at parameter, which can take the values Begin, End, or Random. The end_nodes parameter is a vector containing the IDs of the nodes for which the walks will be generated. For each node in end_nodes, the function produces random walks based on the specified starting point, returning the walks as a mapping of node IDs to their corresponding random walks.
std::vector<std::vector<std::pair<int, int64_t>>> get_random_walks_with_times(WalkStartAt walk_start_at, int end_node=-1)This method generates random walks from the temporal graph where each step in the walk includes the node ID and its corresponding timestamp. The walk_start_at parameter specifies whether to sample the walks from the beginning, end, or randomly. An optional end_node can be specified to control the endpoint of each walk. If -1 is provided, the endpoint is selected randomly. This function returns a vector of walks, where each walk is represented as a sequence of pairs containing the node ID and timestamp.
std::unordered_map<int, std::vector<std::vector<std::pair<int, int64_t>>>> get_random_walks_for_nodes_with_times(WalkStartAt walk_start_at, const std::vector<int>& end_nodes)This method generates timestamped random walks for each specified node in the graph. The walk_start_at parameter indicates the walk's starting point (Begin, End, or Random), and end_nodes is a vector of node IDs for which to generate the walks. The output is a map associating each node ID with a vector of random walks, where each walk contains pairs of node IDs and timestamps.
int get_len_walk();Returns the length of the random walks that will be generated by the TemporalWalk object.
size_t get_edge_count();Returns the total number of directed edges in the temporal graph.
size_t get_node_count();Returns the total number of nodes present in the temporal graph.
std::vector<int> get_node_ids();Returns a vector containing the IDs of all nodes in the temporal graph.
void clear();Clears and reinitiates the underlying temporal graph, removing all edges and nodes.
The Python bindings for the TemporalWalk class provide a seamless way to interact with the C++ implementation from Python. The bindings are created using the pybind11 library, enabling easy access to the functionality of the TemporalWalk class.
TemporalWalk(num_walks: int, len_walk: int, picker_type: str, max_time_capacity: int=-1):Initializes a TemporalWalk object with the specified number of walks, length of each walk, the type of random picker to be used and the maximum time capacity of the graph. The picker_type should be one of the following strings: "Uniform", "Linear", or "Exponential". The default value of max_time_capacity is -1, which means unlimited capacity. If set then edges older than max_time_capacity from the latest timestamp are deleted automatically.
def add_multiple_edges(edge_infos: List[Tuple[int, int, int64_t]]):Adds multiple directed edges to the temporal graph based on the provided list of tuples. Each tuple should contain three elements: the source node u, the destination node i, and the timestamp t.
get_random_walks(walk_start_at: str, end_node: int = -1, fill_value: int = 0) -> np.ndarray:Generates random walks from the temporal graph. The walks can be sampled from destination to source or source to destination, controlled by the walk_start_at parameter, which can be "Begin", "End", or "Random". An end_node can be specified to start or end the walks. The default value -1 picks the end-node randomly. Returns a 2D NumPy array containing the generated walks, padded with fill_value where necessary.
get_random_walks_for_nodes(walk_start_at: str, end_nodes: List[int], fill_value: int = 0) -> Dict[int, np.ndarray]:Generates random walks for multiple specified nodes in the temporal graph. Similar to get_random_walks, the walks can be sampled from destination to source or source to destination, controlled by the walk_start_at parameter. The end_nodes parameter is a list of integers representing the IDs of the nodes for which the walks will be generated. Returns a dictionary of 2D NumPy arrays, each corresponding to the walks for a specific node, padded with fill_value where necessary.
get_random_walks_with_times(walk_start_at: str, end_node: int = -1) -> List[List[Tuple[int, int]]]:Generates timestamped random walks in the temporal graph, where each step contains the node ID and timestamp. The walk_start_at argument controls the sampling point ("Begin", "End", or "Random"), while end_node specifies an optional endpoint. If -1, an endpoint is randomly selected. Returns a list of walks, each represented as a list of tuples containing node IDs and timestamps.
get_random_walks_for_nodes_with_times(walk_start_at: str, end_nodes: List[int]) -> Dict[int, List[List[Tuple[int, int]]]]:Generates timestamped random walks for each specified node in end_nodes. The walk_start_at argument determines the starting point of the walks ("Begin", "End", or "Random"). Returns a dictionary mapping each node ID to a list of walks, where each walk is a list of tuples, with each tuple containing the node ID and timestamp.
get_node_count() -> int:Returns the total number of nodes present in the temporal graph.
get_edge_count() -> int:Returns the total number of directed edges in the temporal graph.
get_node_ids() -> np.ndarray:Returns a numpy array containing the IDs of all nodes in the temporal graph.
clear():Clears and reinitiates the underlying temporal graph, removing all edges and nodes.
add_edges_from_networkx(nx_graph: nx.DiGraph):Adds edges from a NetworkX directed graph to the current TemporalWalk object. The NetworkX graph must have a 'timestamp' attribute for each edge.
to_networkx() -> nx.DiGraph:Exports the current temporal graph to a NetworkX DiGraph object. Each edge in the resulting graph will have a 'timestamp' attribute containing the temporal information.
Nguyen, Giang Hoang et al. “Continuous-Time Dynamic Network Embeddings.” Companion Proceedings of the The Web Conference 2018 (2018).