Fast matrix manipulation library for Elixir implemented in C native code with highly optimized CBLAS sgemm() used for matrix multiplication.
For example, vectorized linear regression is about 13 times faster, than Octave single threaded implementation.
It's also memory efficient, so you can work with large matrices, about billion of elements in size.
Based on matrix code from https://github.com/sdwolfz/exlearn
2015 MacBook Pro, 2.2 GHz Core i7, 16 GB RAM
Operations are performed on 3000×3000 matrices filled with random numbers.
You can run benchmarks from the /bench folder with python numpy_bench.py and MIX_ENV=bench mix bench commands.
benchmark iterations average time
logistic_cost() 1000 1.23 ms/op
np.divide(A, B) 100 15.43 ms/op
np.add(A, B) 100 14.62 ms/op
sigmoid(A) 50 93.28 ms/op
np.dot(A, B) 10 196.57 ms/op
benchmark iterations average time
logistic_cost() 1000 1.23 ms/op (on par)
divide(A, B) 200 7.32 ms/op (~ 2× faster)
add(A, B) 200 7.71 ms/op (~ 2× faster)
sigmoid(A) 50 71.47 ms/op (23% faster)
dot(A, B) 10 213.31 ms/op (8% slower)
Slaughter of the innocents, actually.
2015 MacBook Pro, 2.2 GHz Core i7, 16 GB RAM
Dot product of 500×500 matrices
| Library | Ops/sec | Compared to Matrex |
|---|---|---|
| Matrex | 674.70 | |
| Matrix | 0.0923 | 7 312.62× slower |
| Numexy | 0.0173 | 38 906.14× slower |
| ExMatrix | 0.0129 | 52 327.40× slower |
Dot product of 3×3 matrices
| Library | Ops/sec | Compared to Matrex |
|---|---|---|
| Matrex | 3624.36 K | |
| GraphMath | 1310.16 K | 2.77x slower |
| Matrix | 372.58 K | 9.73x slower |
| Numexy | 89.72 K | 40.40x slower |
| ExMatrix | 35.76 K | 101.35x slower |
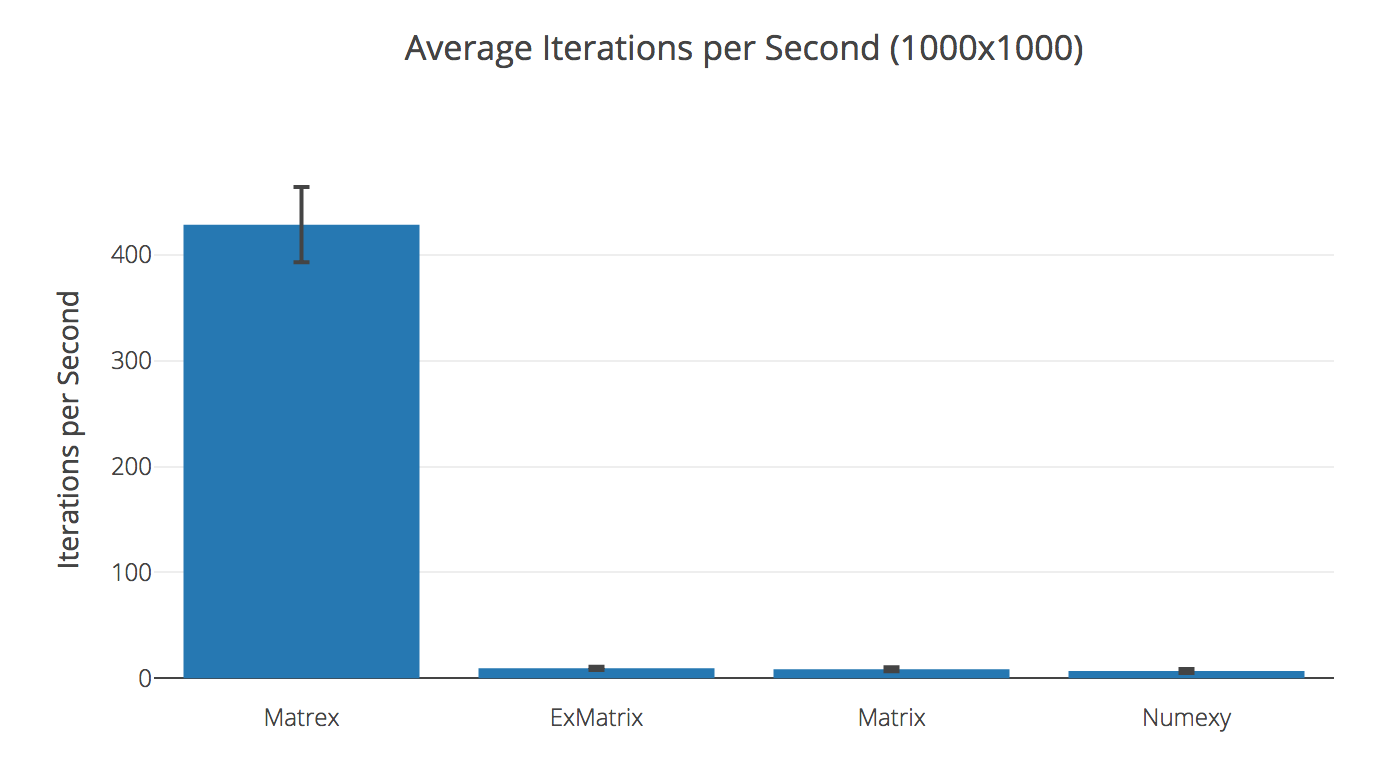
Transposing 1000x1000 matrix
| Library | Ops/sec | Compared to Matrex |
|---|---|---|
| Matrex | 428.69 | |
| ExMatrix | 9.39 | 45.64× slower |
| Matrix | 8.54 | 50.17× slower |
| Numexy | 6.83 | 62.80× slower |
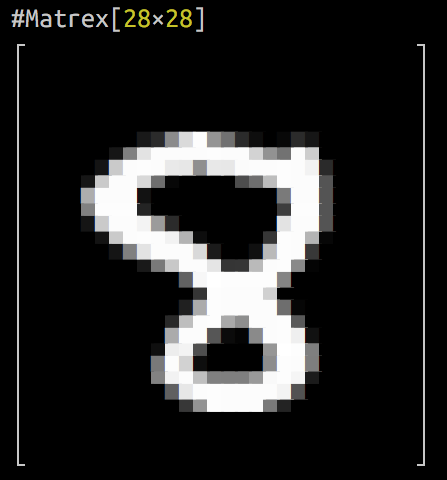
Complete example of Matrex library at work: Linear regression on MNIST digits (Jupyter notebook)
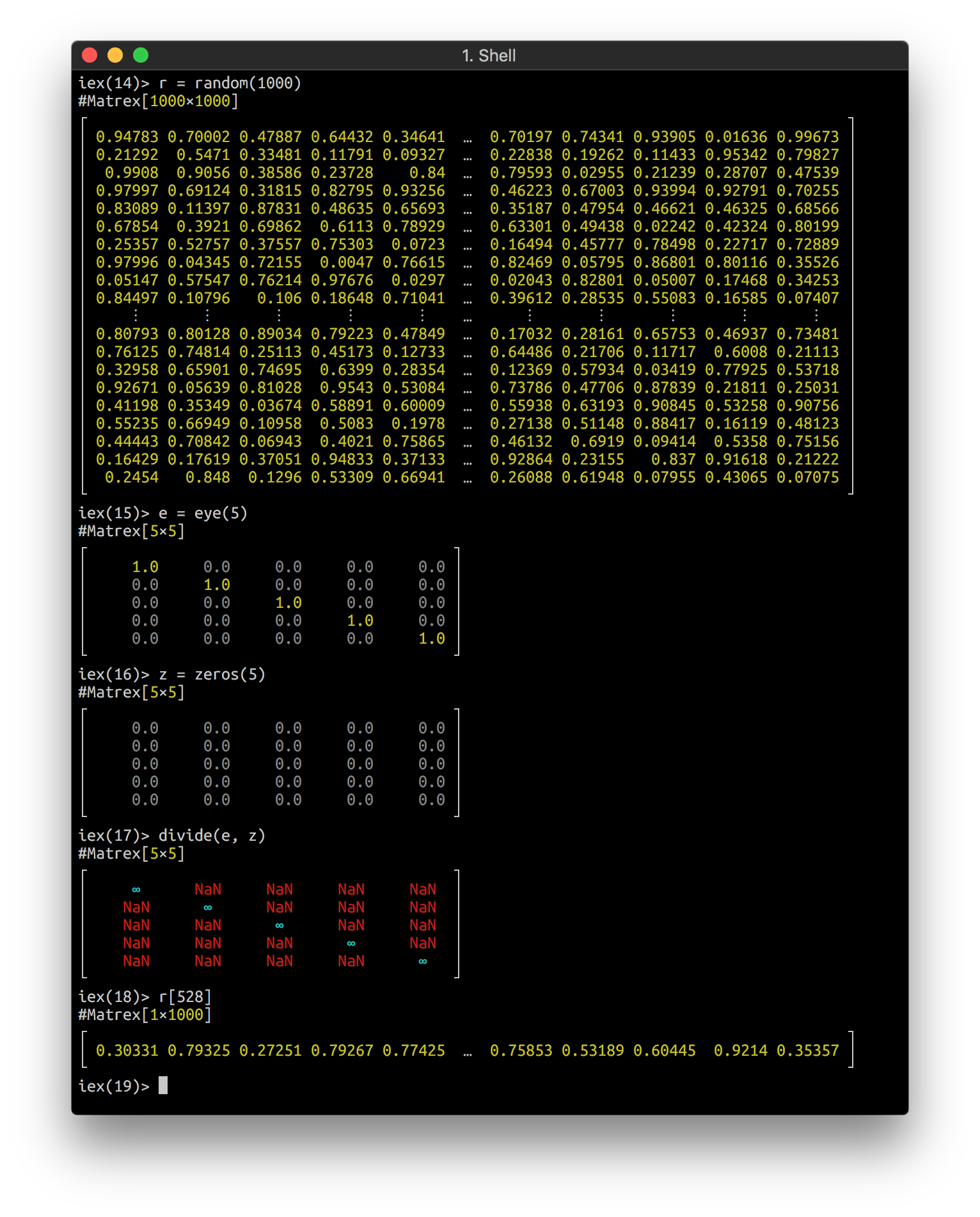
Matrex implements Inspect protocol and looks nice in your console:
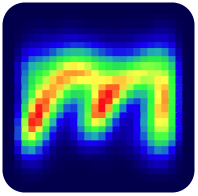
It can even draw a heatmap of your matrix in console! Here is an animation of logistic regression training with Matrex library and some matrix heatmaps:
The package can be installed
by adding matrex to your list of dependencies in mix.exs:
def deps do
[
{:matrex, "~> 0.6"}
]
endEverything works out of the box, thanks to Accelerate framework. If you encounter a compilation error
native/src/matrix_dot.c:5:10: fatal error: 'cblas.h' file not found
then make sure the XCode command-line tools are installed (xcode-select --install).
If the error still not resolved, for MacOS Mojave, run
open /Library/Developer/CommandLineTools/Packages/macOS_SDK_headers_for_macOS_10.14.pkg
to restore /usr/include and /usr/lib.
On MacOS 10.15 this error can be solved with
export CPATH=/Library/Developer/CommandLineTools/SDKs/MacOSX.sdk/usr/include/
or with
C_INCLUDE_PATH=/Library/Developer/CommandLineTools/SDKs/MacOSX.sdk/System/Library/Frameworks/Accelerate.framework/Frameworks/vecLib.framework/Headers mix compile
You need to install scientific libraries for this package to compile:
> sudo apt-get install build-essential erlang-dev libatlas-base-devIt will definitely work on Windows, but we need a makefile and installation instruction. Please, contribute.
With the help of MATREX_BLAS environment variable you can choose which BLAS library to link with.
It can take values blas (the default), atlas, openblas or noblas.
The last option means that you compile C code without any external dependencies, so, it should work anywhere with a C compiler place:
$ mix clean
$ MATREX_BLAS=noblas mix compileAccess behaviour is partly implemented for Matrex, so you can do:
iex> m = Matrex.magic(3)
#Matrex[3×3]
┌ ┐
│ 8.0 1.0 6.0 │
│ 3.0 5.0 7.0 │
│ 4.0 9.0 2.0 │
└ ┘
iex> m[2][3]
7.0Or even:
iex> m[1..2]
#Matrex[2×3]
┌ ┐
│ 8.0 1.0 6.0 │
│ 3.0 5.0 7.0 │
└ ┘There are also several shortcuts for getting dimensions of matrix:
iex> m[:rows]
3
iex> m[:size]
{3, 3}calculating maximum value of the whole matrix:
iex> m[:max]
9.0or just one of it's rows:
iex> m[2][:max]
7.0calculating one-based index of the maximum element for the whole matrix:
iex> m[:argmax]
8and a row:
iex> m[2][:argmax]
3Matrex.Operators module redefines Kernel math operators (+, -, *, / <|>) and
defines some convenience functions, so you can write calculations code in more natural way.
It should be used with great caution. We suggest using it only inside specific functions
and only for increased readability, because using Matrex module functions, especially
ones which do two or more operations at one call, are 2-3 times faster.
def lr_cost_fun_ops(%Matrex{} = theta, { %Matrex{} = x, %Matrex{} = y, lambda } = _params)
when is_number(lambda) do
# Turn off original operators
import Kernel, except: [-: 1, +: 2, -: 2, *: 2, /: 2, <|>: 2]
import Matrex.Operators
import Matrex
m = y[:rows]
h = sigmoid(x * theta)
l = ones(size(theta)) |> set(1, 1, 0.0)
j = (-t(y) * log(h) - t(1 - y) * log(1 - h) + lambda / 2 * t(l) * pow2(theta)) / m
grad = (t(x) * (h - y) + (theta <|> l) * lambda) / m
{scalar(j), grad}
endThe same function, coded with module methods calls (2.5 times faster):
def lr_cost_fun(%Matrex{} = theta, { %Matrex{} = x, %Matrex{} = y, lambda } = _params)
when is_number(lambda) do
m = y[:rows]
h = Matrex.dot_and_apply(x, theta, :sigmoid)
l = Matrex.ones(theta[:rows], theta[:cols]) |> Matrex.set(1, 1, 0)
regularization =
Matrex.dot_tn(l, Matrex.square(theta))
|> Matrex.scalar()
|> Kernel.*(lambda / (2 * m))
j =
y
|> Matrex.dot_tn(Matrex.apply(h, :log), -1)
|> Matrex.subtract(
Matrex.dot_tn(
Matrex.subtract(1, y),
Matrex.apply(Matrex.subtract(1, h), :log)
)
)
|> Matrex.scalar()
|> (fn
:nan -> :nan
x -> x / m + regularization
end).()
grad =
x
|> Matrex.dot_tn(Matrex.subtract(h, y))
|> Matrex.add(Matrex.multiply(theta, l), 1.0, lambda)
|> Matrex.divide(m)
{j, grad}
endMatrex implements Enumerable, so, all kinds of Enum functions are applicable:
iex> Enum.member?(m, 2.0)
true
iex> Enum.count(m)
9
iex> Enum.sum(m)
45For functions, that exist both in Enum and in Matrex it's preferred to use Matrex
version, beacuse it's usually much, much faster. I.e., for 1 000 x 1 000 matrix Matrex.sum/1
and Matrex.to_list/1 are 438 and 41 times faster, respectively, than their Enum counterparts.
You can save/load matrix with native binary file format (extra fast) and CSV (slow, especially on large matrices).
Matrex CSV format is compatible with GNU Octave CSV output, so you can use it to exchange data between two systems.
iex> Matrex.random(5) |> Matrex.save("rand.mtx")
:ok
iex> Matrex.load("rand.mtx")
#Matrex[5×5]
┌ ┐
│ 0.05624 0.78819 0.29995 0.25654 0.94082 │
│ 0.50225 0.22923 0.31941 0.3329 0.78058 │
│ 0.81769 0.66448 0.97414 0.08146 0.21654 │
│ 0.33411 0.59648 0.24786 0.27596 0.09082 │
│ 0.18673 0.18699 0.79753 0.08101 0.47516 │
└ ┘
iex> Matrex.magic(5) |> Matrex.divide(Matrex.eye(5)) |> Matrex.save("nan.csv")
:ok
iex> Matrex.load("nan.csv")
#Matrex[5×5]
┌ ┐
│ 16.0 ∞ ∞ ∞ ∞ │
│ ∞ 4.0 ∞ ∞ ∞ │
│ ∞ ∞ 12.0 ∞ ∞ │
│ ∞ ∞ ∞ 25.0 ∞ │
│ ∞ ∞ ∞ ∞ 8.0 │
└ ┘Float special values, like :nan and :inf live well inside matrices,
can be loaded from and saved to files.
But when getting them into Elixir they are transferred to :nan,:inf and :neg_inf atoms,
because BEAM does not accept special values as valid floats.
iex> m = Matrex.eye(3)
#Matrex[3×3]
┌ ┐
│ 1.0 0.0 0.0 │
│ 0.0 1.0 0.0 │
│ 0.0 0.0 1.0 │
└ ┘
iex> n = Matrex.divide(m, Matrex.zeros(3))
#Matrex[3×3]
┌ ┐
│ ∞ NaN NaN │
│ NaN ∞ NaN │
│ NaN NaN ∞ │
└ ┘
iex> n[1][1]
:inf
iex> n[1][2]
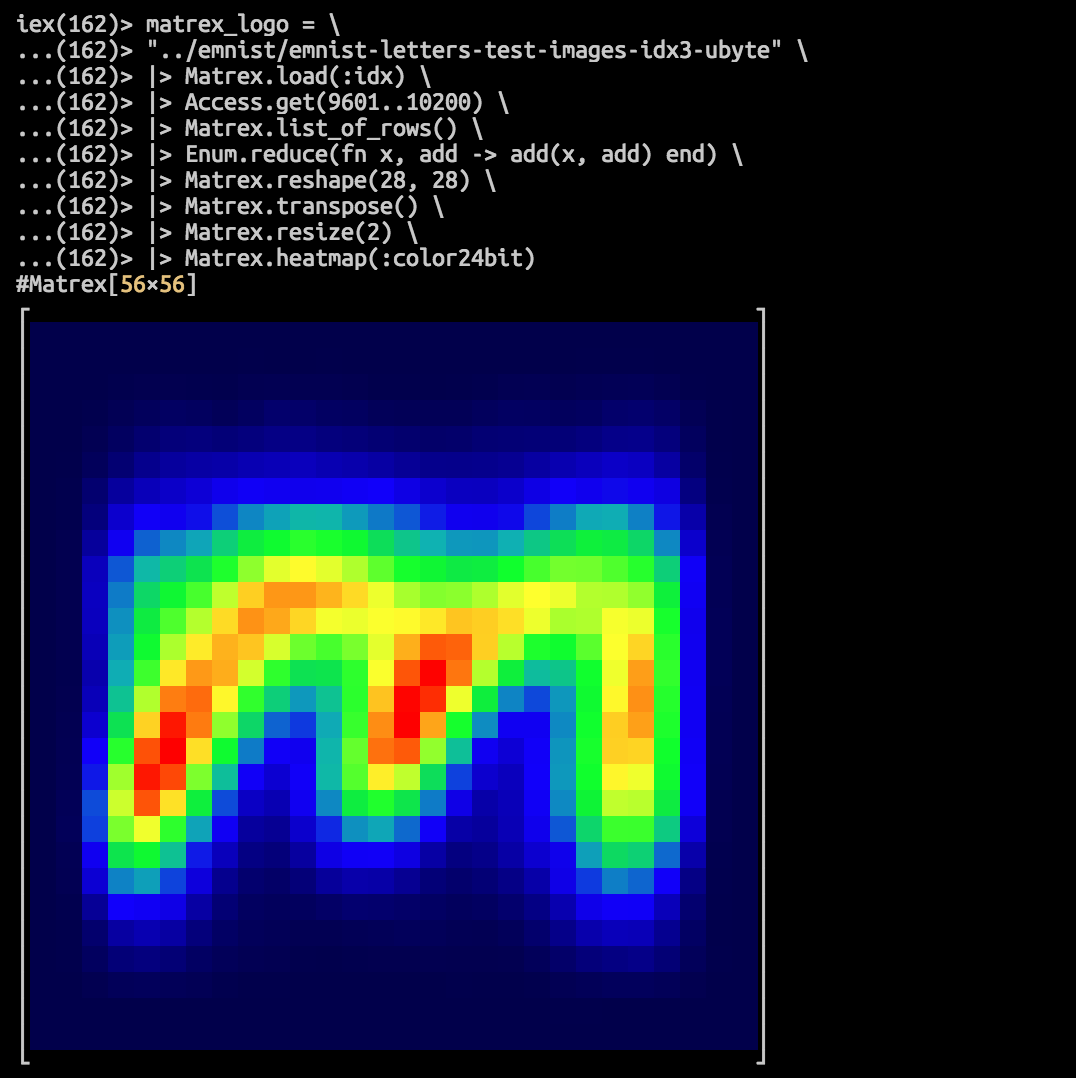
:nan iex(166)> matrex_logo = \
...(166)> "../emnist/emnist-letters-test-images-idx3-ubyte" \
...(166)> |> Matrex.load(:idx) \
...(166)> |> Access.get(9601..10200) \
...(166)> |> Matrex.list_of_rows() \
...(166)> |> Enum.reduce(fn x, sum -> add(x, sum) end) \
...(166)> |> Matrex.reshape(28, 28) \
...(166)> |> Matrex.transpose() \
...(166)> |> Matrex.resize(2) \
...(166)> |> Matrex.heatmap(:color24bit)