- A.Bugatti - Guida teoria olimpiadi di informatica (sesta edizioni)
- Theory of programming, graph theory.
- Corso di informatica C e C++, vol B - HOEPLI.
- OLINFO - [PO2021] Algoritmi e nozioni base sui grafi
E’ una struttura dati descritta da nodi (anche detti link o vertici) e archi (o lati), che uniscono una coppia di nodi.
Si definiscono:
-
Nodi → Elemento base che lo compone, possono essere interni, cioè a loro volta collegati ad altri nodi mediante archi, oppure foglie, cioè nodi terminali, che non hanno archi uscenti.
-
Archi → Collegamenti tra nodi, possono essere orientati o non, pesati o non.
Possono anche collegarsi allo stesso nodo.
Ogni nodo interno, ha dei figli, se non ha figli è un nodo foglia.
- Grado uscente di un nodo: numero di figli che esso ha.
- Grado entrante di un nodo: numero di archi entranti nel nodo.
- Ciclo: cammino che permette partendo da un nodo A, di tornare allo stesso nodo, senza mai attraversare per più di una volta gli stessi archi e nodi.
- Circuito: cammino che permette partendo da un nodo A, di tornare allo stesso nodo, senza mai attraversare per più di una volta lo stesso arco
Archi pesati → Percorrere un determinato cammino/arco, ha un “costo” (può essere anche una distanza,un periodo di tempo, è utilizzando un grafo con archi pesati che determino cammini massimi/minimi) 👇🏻
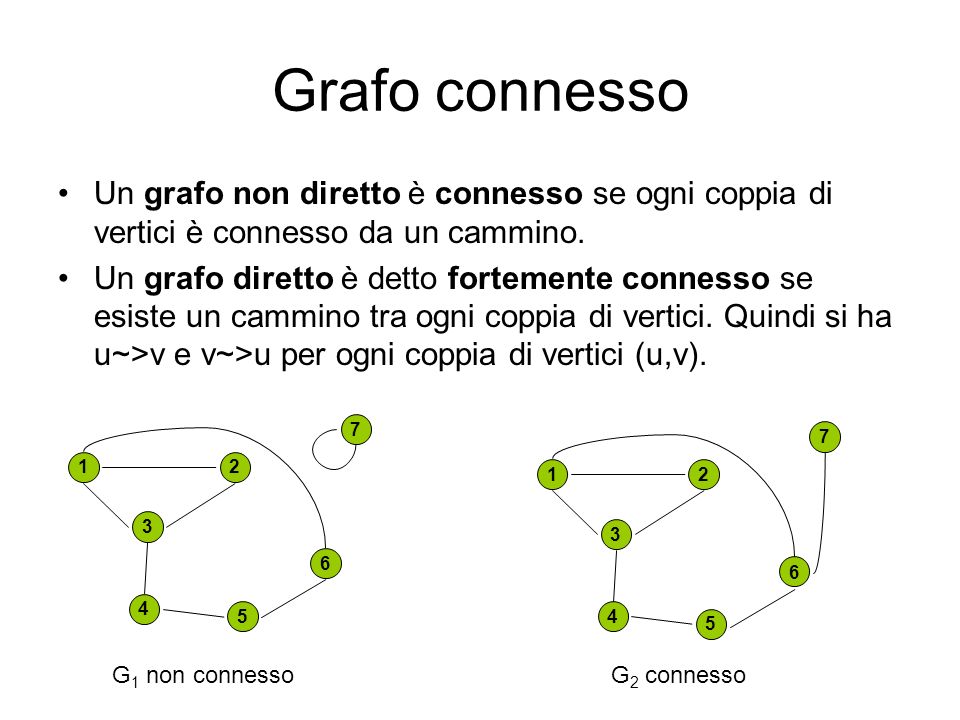
Grafo connesso → Grafo in cui ogni nodo è collegato al resto dei nodi da almeno un cammino (arco), cioè non ci sono nodi “orfani”.
Queste proprietà sono ovviamente combinabili, per esempio, il grafo seguente, è connesso (tutti i nodi sono collegati agli altri da almeno un arco), pesato, e orientato 👇🏻
Grafi bipartiti → Un grafo è bipartito se posso “suddividerlo” in due insiemi in modo che ogni arco abbia un estremità in un nodo appartenente al gruppo A, e un’altra nel gruppo B 👇🏻
Grafi euleriani → Grafo che contiene almeno un circuito di Eulero, (vedi definizione di circuito qui sopra) cioè un percorso che passa per tutti i nodi, senza mai passare per più di una volta per ogni arco (è possibile però raggiungere più volte uno stesso nodo, basta non raggiungerlo seguendo un arco precedentemente già attraversato).
Per esempio, vi sarà sicuramente capitato di risolvere questo indovinello, per cui la soluzione richiede di ricreare la figura in foto, senza mai percorrere uno stesso “arco”.
💡 Come possiamo intuire, la ***soluzione*** di questo problema, ***richiede l’identificazione di un circuito Euleriano***, e quindi della determinazione di un ***Grafo Euleriano***, la cui forma componga quella di una busta.Grafi Hamiltoniani → E’ Detto un grafo Hamiltoniano, un grafo che contiene almeno un ciclo Hamiltoniano, cioè un cammino che permette di visitare tutti i vertici (o nodi) di un grafo, attraversandoli solo una volta.
La soluzione di alcuni problemi che richiedono l’identificazione di un ciclo Hamiltoniano, sono stati tuttavia classificati come Intrattabili (ma computabili!), in quanto la complessità di questo tipo di problemi sarebbe di tipo esponenziale, in base al numero di vertici (nodi) di cui è composto il grafo studiato.
Hamilton stesso si è interessato solo a fornire la definizione di un ciclo Hamiltoniano, ma non allo studio di un algoritmo di identificazione di esso.
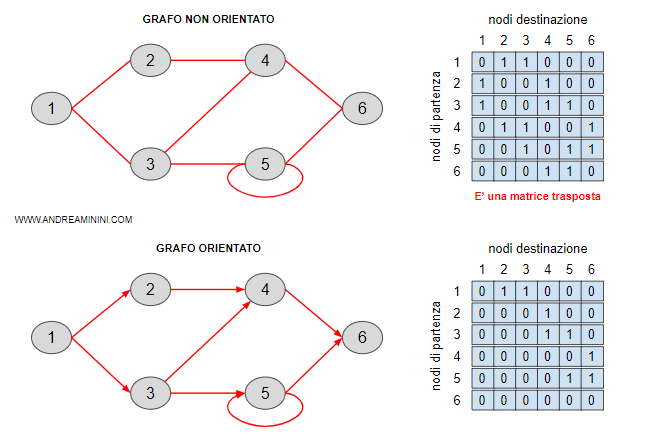
Rappresento grafi pesati o non pesati, con una matrice di adiacenza:
- Metto nella colonna più a sinistra,i nodi di “sorgente”.
- Nella riga più in alto, pongo i nodi di “destinazione”.
In caso non ci fossero archi che uniscono un determinato nodo ad un altro, indico che da quel nodo non ci sono percorsi per una determinata destinazione, con il valore “infinito” ( o 0 ).
💡 Nel caso volessi rappresentare un grafo pesato mediante matrice di adiacenza, pongo in ogni casella il peso di un determinato arco, se esso esiste, altrimenti pongo un valore diverso da 0, in quanto possono esistere archi di “peso” = 0. (Generalmente INFINITO)La rappresentazioni di grafi pesati mediante matrici di adiacenza, produce una matrice o tabella, di dimensione n*n, dove n è il numero di nodi presenti nel mio grafo. 👇🏻
Posso ottimizzare questa rappresentazione, semplificandola utilizzando due strutture dati, ciascuna rappresentante gli archi e i nodi.
Un grafo, definito come insieme di archi e nodi, può essere rappresentato in memoria con:
- Un Array di Nodi
- In cui ogni nodo, contiene un insieme (un altro Array) di coppie di valori (sorgente, destinazione), cioè gli archi (orientati o meno)
Rappresentazione di un arco in memoria 👇🏻
struct arco_t{
int peso_dell'arco;
int nodo_di_destinazione;
}Rappresentazione di un nodo in memoria 👇🏻
struct nodo_t{
int distanza = INFINITO; //inizializzo a INFINITO, per indicare
//che quel determinato
//nodo non è ancora stato visitato.
vector<arco_t> insieme_archi_uscenti_dal_nodo; //un insieme di archi uscenti
}Decido di tener traccia dei soli archi uscenti dal nodo rappresentato, gli archi entranti in quel nodo saranno rappresentato come archi uscenti da altri nodi adiacenti.
struct arco_t{
int nodo_di_destinazione;
int peso_dell'arco;
}
struct nodo_t{
vector<arco_t> insieme_archi_uscenti_dal_nodo;
}
int main(void){
int numero_di_nodi=4;
vector<nodo_t> vettore_di_nodi(numero_di_nodi);
//rappresento i soli archi USCENTI da ogni nodo
//parto dal nodo "1".
vettore_di_nodi[0].insieme_archi_uscenti_dal_nodo.emplace_back(3,3)
//destinazione -> nodo 3, peso -> 3.
vettore_di_nodi[0].insieme_archi_uscenti_dal_nodo.emplace_back(4,5)
//destinazione -> nodo 4, peso -> 5.
//nodo "2".
vettore_di_nodi[1].insieme_archi_uscenti_dal_nodo.emplace_back(3,7)
//destinazione -> nodo 3, peso -> 7.
vettore_di_nodi[1].insieme_archi_uscenti_dal_nodo.emplace_back(4,9)
//destinazione -> nodo 4, peso -> 9.
//nodo "3".
vettore_di_nodi[2].insieme_archi_uscenti_dal_nodo.emplace_back(1,3)
//destinazione -> nodo 1, peso -> 3.
vettore_di_nodi[2].insieme_archi_uscenti_dal_nodo.emplace_back(2,7)
//destinazione -> nodo 2, peso -> 7.
return 0;
}Operazioni di “visita” del grafo → Un algoritmo che permette di “scorrere”, di visitare ogni nodo che compone il mio grafo,in base ad un determinato ordine/criterio,senza entrare in loop (cammini ciclici da cui non riesco ad uscire):
Definisco di partire a visitare il mio grafo/una parte di esso, da un nodo “sorgente”, che identifico ponendo la sua distanza a 0, in una situazione in cui tutti gli altri nodi hanno distanza da esso pari a INFINITO (in quanto non sono ancora stati visitati).
Operazioni di visita 👇🏻
-
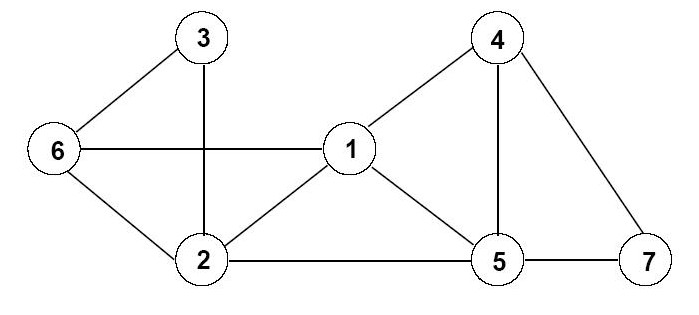
DFS (Depth-First-Search) → Si basa su una pila, generalmente non è utilizzato per calcolare percorsi su grafi pesati.
Inizio da un nodo per cui pongo la distanza a 0, e visito UNO dei nodi ad esso adiacenti, che non sia già stato visitato (nodo vicino) 👇🏻
Inizio dal nodo “3”, e visito uno dei suoi nodi vicini, a caso, in questo caso partiamo dal nodo 1.
Visito il nodo 1, lo aggiungo alla pila, e riparto da esso a visitare uno dei suoi nodi vicini, in questo caso o zero o due (scelgo 0).
Non prendo in considerazione in nodo 3, in quanto già stato visitato.
Ripeto l’operazione per tutti i nodi, quindi visito il nodo “0”, lo aggiungo alla pila, e visito uno dei suoi nodi vicini (2).
Vado avanti finchè il nodo in cui mi trovo, non ha nessun nodo non visitato 👇🏻
Ora il nodo 7, ha come nodi vicini solo 6 e 4, entrambi già visitati, pertando inizio ad estrarre dalla pila i nodi, e torno “indietro” nel cammino che ho percorso, finchè non estraggo un nodo che ha ancora nodi da visitare.
Essendo una pila, ripercorro il mio cammino a restroso, quindi estraggo il nodo 6.
Il nodo 6, ha come nodo ancora non visitato il nodo 8, pertanto lo visito.
Di nuovo, il nodo 8 non ha nodi ancora da visitare, quindi torno indietro nel mio cammino (estraggo dalla coda).
Estraggo il nodo 6, ma esso non ha altri nodi da visitare, estraggo nuovamente un nodo.
Estraggo il nodo 4, ma ha come nodi adiacenti solo i nodi 6 e 7, entrambi già visitati, quindi estraggo ancora.
Continuo ad estrarre, finchè non arrivo al nodo 1, che ha come nodo ancora da visitare il nodo 5, procedo quindi a visitarlo.
Il nodo 5, non ha altri nodi non visitati, riestraggo un altro nodo (torno in 1).
Dal nodo uno, non ho altri nodi non visitati, pertanto torno al nodo 3.
Sono ritornato al nodo di partenza, la pila è vuota, l’algoritmo termina.
-
BFS (Breadth-First-Search) → Complessità computazionale = O(Numero nodi + Numero archi) → Visito prima tutti i nodi a distanza I, prima di passare alla visita di nodi (I + Peso arco).
Inizio da un nodo per cui pongo la distanza a 0, e visito tutti i nodi ad esso adiacenti (i nodi vicini) 👇🏻
(In questo esempio, gli archi vanno intesi con peso unitario, 1).
Decido di iniziare dal nodo 3 (pongo infatti la sua distanza a 0).
Visito tutti i nodi vicini (quindi i nodi direttamente connessi a 3, 1,5 e 4), e mi ricordo quali nodi ho visitato in una coda.
Visito in ordine 1,4,5 (come nella coda scritta nell’angolo dell’immagine), e aggiorno i campi “distanza” di ogni nodo, se sono riuscito a raggiungerlo con un valore di distanza minore.
In questo caso, i nodi 1,5,4, hanno un valore “distanza” pari a infinito, in quanto non sono ancora stati visitati, pertanto aggiorno i loro campi con 👇🏻
Valore peso nodo precedente + peso arco.
In questo caso, 0 + 1 (peso nodo 3 + arco unitario).
Estraggo ora gli elementi appena visitati, e procedo nuovamente a visitare i vicini di quest’ultimi.
Visito quindi uno ad uno i vicini di 1, poi di 5 e infine di 4.
Visito i vicini di “1”, i nodi 0 e 2.
💡 Notiamo come visito il nodo 5, in quanto “vicino” del nodo 1 attualmente in analisi, tuttavia la sua distanza per raggiungerlo passando per il nodo 1, sarebbe (Valore peso nodo precedente + peso arco), quindi 1+1 =2.Nel nodo 5 però, c’è un valore di “distanza” pari a 1, che indica che so già raggiungere quel nodo con una distanza minore (cammino diretto da 3 a 5), pertanto NON AGGIORNO il valore di distanza di 5!.
Visito però i nodi 0 e 2, che non sono mai stati visitati, quindi sostituisco i loro valori di “distanza” (attualmente pari a INFINITO), con (Valore peso nodo precedente + peso arco), quindi 2 per entrambi.
Visito i vicini di “4”, i nodi 6 e 7.
Non ho mai visitato questi nodi, quindi sostituisco INFINITO (valori di “distanza” attualmente presenti nei rispettivi campi dei nodi), con (Valore peso nodo precedente + peso arco), quindi 1+1=2.
Il nodo 5, ha come vicino solo il nodo “1”, che posso raggiungere con una “distanza” pari a 2; so però che sono già in grado di raggiungere il nodo “1” con un costo pari a 1, pertanto non ne aggiorno il valore di distanza.
L’algoritmo di Dijkstra, si basa sulla visita BFS, e permette di identificare i percorsi minimi in un grafo orientato o non orientato (quindi grafi ciclici e aciclici), importante che per ogni arco sia assegnato un costo NON NEGATIVO (può essere anche zero, ma è importante che non siano a peso negativo in quanto l’algoritmo potrebbe non funzionare).
Potrei infatti percorrere più volte un arco a peso negativo, facendo diminuire il costo totale del percorso verso un altro vertice, in modo che tenda ad un valore vicino a -Infinito.
E’ possibile utilizzare Dijkstra per determinare i percorsi più brevi da un vertice a cui pongo distanza 0, a tutti gli altri nodi del grafo, ma generalmente è utilizzato parzialmente, fino ad identificare il percorso più breve per un determinato nodo, e non per tutti.
Ogni nodo, è descritto da due informazioni, il nodo da cui può essere raggiunto, e il costo per cui quel determinato nodo può raggiungerlo.
Per l’algoritmo di Dijkstra, parto da un nodo “sorgente”, a cui pongo volutamente il campo del “costo” a 0, in quanto posso raggiungere quel nodo direttamente partendo da esso (come fosse un arco che torna a se stesso), con costo pari a zero.
Partendo da quel nodo, analizzo ogni arco uscente da esso, e mi posiziono nel nodo “di destinazione”.
Parto dall’arco di peso 5, ma è indifferente in quanto per ogni nodo devo analizzarne tutti gli archi prima di “scartarli”.
💡 Nel nodo di destinazione, confronto il costo impiegato per arrivare da esso, partendo dal nodo precedente (costo nodo precedente + costo arco pesato), e se è minore del dato attualmente presente nel campo “costo” del nodo in cui mi trovo, aggiorno il campo corrispondente al nodo di destinazione, e aggiorno anche il costo.Costo per arrivare al nodo 1 → 0 + 5 = 5.
Ripeto questa operazione per tutti gli archi uscenti del nodo corrente, prima di scartarlo.
Procedo ad analizzare l’arco uscente di peso 2.
E l’arco di peso 1 👇🏻
💡 Ho analizzato tutti gli archi uscenti dal nodo “0”, posso scartarlo.Il nodo non ancora espanso più vicino a “0”, è il nodo 3.
Ripeto la stessa operazione con il nodo 3, ne visito quindi tutti i nodi vicini, procedendo a sostituire il “costo” necessario per arrivare ad esso, se minore di quello già presente al suo interno.
I “Vicini” del nodo 3 sono il nodo 2 e il nodo 4.
Per arrivare al nodo “2”, dovrei impiegare un costo totale di 1+6, ma io so già arrivare nel nodo “2”, seguendo un percorso diretto a costo 2, che è minore dei 7 proposti dal percorso 0-3-2, pertanto NON AGGIORNO IL COSTO RELATIVO AL NODO 2.
Visito il prossimo vicino, il nodo “4”.
Il prossimo nodo non espanso, a distanza minima da 0 è il nodo “2”, procedo ad espanderlo.
Ripeto la stessa operazione con il nodo 2, ne visito quindi tutti i nodi vicini, procedendo a sostituire il “costo” necessario per arrivare ad esso, se minore di quello già presente al suo interno.
I vicini del nodo 2 sono il nodo 1 e il nodo 7.
L’Ultimo nodo rimasto da visitare, non ancora espanso, visino al nodo 0, è il nodo 1.
💡 Tra i nodi vicini a 1, ci sarebbe anche il nodo 2, che posso raggiungere con un costo di 3+1, ma so già raggiungere il nodo 2 con un costo di “2”, qundi NON AGGIORNO IL RELATIVO COSTO.Il nodo a distanza minima non espanso, è il nodo 5, lo espando.
💡 Ripeto questa operazione per tutti i nodi, e quando non avrò più archi uscenti da analizzare, potrò trovare nei campi corrispondenti al nodo di destinazione, i dati che indicano il costo minimo per raggiungerlo, e il nodo ad esso precedente nel percorso indicato.Percorrendo a retroso i campi “ID Nodo precedente”, dei vari nodi, posso ricreare il percorso indicato.
L’insieme degli archi che compongono il percorso minimo, formano un “albero dei cammini minimi”.
Si dimostra, che per determinare il percorso minimo tra due vertici, mi basta arrivare ad esso, senza espanderlo, perchè se mi trovo nella situazione di espandere il nodo stesso, vuol dire che ho già determinato il percorso minimo per esso, pertanto esso non verrà più aggiornato,riducendo la complessità da O(N+M) a O(N log N).
Risolve il problema dell’algoritmo di Dijkstra, per cui non è possibile analizzare grafi con archi a peso negativo.
Si possono quindi studiare i cammini minimi di un grafo orientato.
Ciò accade perchè alla prima iterazione di Dijkstra, non viene assicurato che siano identificati i cammini a costo minimo.
💡 Applico quindi l’Algoritmo di Dijkstra, partendo da uno stesso nodo sorgente, tante volte finchè l’algoritmo non produrrà più cambiamenti nelle distanze relative a ogni nodo del grafo.Si dice minimum-spanning-tree, un albero che passa per tutti i nodi del grafo iniziale, impiegando un peso totale minimo per collegare tutti i nodi che lo compongono.
Possono esserci più minimum spanning tree, di costo uguale, in uno stesso grafo.
Sfrutto l’idea per cui tengo un insieme degli archi scelti per formare il mio spanning tree, che può solo crescere, e a cui non posso quindi mai togliere archi.
-
Algoritmo di Kruskal
Ordino gli archi per peso minore, e li scorro in ordine crescente (elaboro prima gli archi a peso minore).
Se l’arco è utile, lo inserisco all’insieme degli archi che comporranno il minimum spanning tree, altrimento lo scarto.
E’ detto arco utile, un arco che non mi permette di formare un ciclo (Un percorso chiuso, per cui posso tornare al nodo di partenza, senza percorrere a retroso gli archi).
L’Algoritmo termina, quando tutti i nodi risulteranno connessi all’interno del mio albero.
Quando tutti i nodi risultano connessi, scarto automaticamente i nodi rimanenti.
Un albero ,è un tipo di grafo, non orientato, connesso e aciclico,in cui non esistono percorsi chiusi
💡 Un albero per definizione, è composto da N nodi, e N-1 Archi.E’ una struttura detta ricorsiva perchè un arco punta a sua volta a un altro nodo, il quale è un altro albero (ogni nodo può essere visto come “root/radice” di un altro sotto-albero).
- NODO PADRE: è un nodo dal quale esce almeno un arco che lo collega ad un nodo figlio;
- NODO FIGLIO: è un nodo che possiede un arco entrante che lo collega ad un nodo padre;
- NODO ANTENATO (Nonno): un nodo si dice antenato di un altro nodo, se è padre del padre di quel nodo.
il nodo A, è padre del padre di D, quindi A è antenato di D.
- NODO DISCENDENTE (Nipote di nonno): un nodo A è discendente di B, se B è antenato di A (non c’è una definizione più specifica).
- NODI FRATELLI: Due nodi si dicono fratelli, se si trovano su uno stesso livello, e discendono da uno stesso nodo padre.
- NODO RADICE: Il nodo “root” (o radice) da cui parte la struttura, è detto “di livello 0”, in quanto non ha nessun arco entrante, a differenza degli altri nodi sottostanti.
- NODO INTERNO: è un nodo che non è né radice né foglia e che quindi possiede un arco entrante e almeno un arco uscente;
- NODO FOGLIA: è un nodo che non possiede archi uscenti (è solo un nodo figlio, sono detti nodi foglia i nodi situati su ad una qualsiasi profondità, non necessariamente a quella massima);
- GRADO DI UN NODO: viene chiamato grado di un nodo il numero di figli, o di sottoalberi, di un nodo;
- LIVELLO O PROFONDITA’ DI UN NODO: il livello di un nodo in un albero è pari a 1 più il livello del nodo padre, intendendo che la radice ha livello 0. Per esempio un nodo figlio della radice sarà di livello 1, suo figlio sarà di livello 2;
- ALTEZZA O PROFONDITA’ DI UN ALBERO: livello del nodo foglia a profondità massima (specificando che la radice è intesa a livello 0)
-
Visita in ampiezza (Breath First Search) o Visita per livello/i → Visita che punta a “scendere in profondità” nel grafo, in modo graduale tra i rami.
Visito questo albero, visitando gradualmente da sinistra verso destra ogni livello, dall’alto verso il basso.
L’Ordine di visita di quest’albero risulterà 👇🏻
L’Ordine di visita del seguente albero secondo la visita per livelli risulta → G E F A B C D.
-
Visita in profondità (Depth First Search) → Visita che punta “ad esplorare” il nodo, andando fino a profondità massima, a scoprire fino a che punto posso spingermi a visitare, per poi eventualmente tornare indietro e visitare nodi tralasciati.
Ci sono tipi di visità in profondità 👇🏻
-
Visita in Preorder → Prima visito il nodo, poi visito ancora in PreOrder il figlio sinistro, poi in PreOrder il figlio destro.
Esempio 👇🏻
Seguendo la definizione della visita in Preorder e partendo dalla radice, visito A, poi parto a visitare in Preorder il figlio sinistro, quindi visito B, e visito a sua volta in Preorder il suo figlio sinistro, quindi C (C non ha figli quindi finisce la visita in Preorder del ramo sinistro di B).
Per il nodo B, ho finito la visita in Preorder del nodo sinistro, quindi visito in Preorder il nodo D (che non ha figlio,quindi finisce la visita in Preorder del nodo B).
Il Nodo A ha ora finito di visitare in Preorder il sottoalbero SX “B”, quindi ripete la visita in Preorder per il ramo DX, in ordine E, poi visita in Preorder del suo nodo SX, (F), e infine (G).
-
Visita in PostOrder → Per ogni nodo,prima visito in PostOrder il figlio SX, poi in PostOrder il figlio DX, poi il nodo stesso.
Esempio 👇🏻
Seguendo la definizione della visita in Postorder, partendo dal nodo A, visito in Postorder il suo figlio SX, quindi visito in Postorder il nodo b.
Visitando in Postorder in nodo B, visito prima il nodo C, (ora la visita in Postorder del figlio SX di B è terminata, quindi vado a visitare in Postorder il suo figlio DX, quindi D).
Per il nodo B, ho finito sia la visita del figlio SX che la visita del figlio DX, quindi passo a visitare il nodo stesso, quindi B.
Per il nodo A, ho ora finito la visita in Postorder del figlio SX, quindi passo a visitare analogamente il figlio DX, quindi in ordine F,G,E.
Ho finito per il nodo A, anche la visita in Postorder del sottoramo DX,quindi visito il nodo stesso (A).
-
Visita inOrder → Per ogni nodo,prima visito in” inOrder” il figlio SX, poi il nodo di partenza, poi in “inOrder” il figlio DX.
-
💡 Un albero è detto K-ario, se il massimo numero di figli di un nodo che lo compone è K.
(Un albero i cui nodi possiedono al massimo 4 figli, è detto quaternario.)
Se in un albero K-ario, tutti i nodi interni (tutti i nodi eccetto radice e foglie) hanno grado uscente K (hanno K figli), e le foglie hanno tutte stessa profondità (sono tutte sullo stesso livello), esso è detto albero completo.
E’ un albero in cui ogni nodo padre, ha al massimo due figli. (diramazione destra e sinistra).
💡 In quanto l’albero è definita una struttura ricorsiva, possiamo definire i figli destro e sinistro di un nodo padre, come radici di due sottoalberi (a destra e a sinistra).Posso definire la struttura di un albero, come una linked list di nodi, per cui ogni nodo però, possiede due informazioni (puntatore), a due nodi successivi, rispettivamente figlio destro e sinistro 👇🏻
typedef struct Nodo{
int info;
Nodo *sinistro;
Nodo *destro;
}NodoBin;Strutture che semplificano le operazioni di:
- inserimento di un elemento
- cancellazione di un elemento
- ricerca di un elemento
- determinazione del massimo/minimo tra i nodi che compongono l’albero
- ricerca del predecessore, cioè del primo elemento maggiore di un elemento dato
- ricerca del successore, cioè del primo elemento minore di un elemento dato
Secondo la sua definizione quindi, il valore contenuto nella radice dell’albero, è un valore che si trova “nel mezzo” tra quelli che compongono la struttura dell’ABR.
bool BinarySearch(int chiaveDaCercare, Nodo Radice) {
if (chiaveDaCercare == Radice -> Value) {
return (true);
} else {
if (chiaveDaCercare < Radice -> Value)
return (BinarySearch(chiaveDaCercare , Radice -> SX));
else
return (BinarySearch(chiaveDaCercare , Radice -> DX));
}
}