TiPI fixes #29
Open
TiPI fixes #29
Conversation
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
get updates from original master
…pzig.de/research/supplementary/TiPI2013/` with `pimax.cpp` being replaced by the `lpzrobots` version.
…n fact $a_{t-1} = K(s_t)$ and thus doesn't equal $a_{t-1} = C_{t-1} * s_{t-1} + h_{t-1}$
…then will be wrong for learning, hence always enter `learn()`
… iteration seems to compute the weight update with adding $C_{t-1}$ to the change within the sum. Results are the same as before for $\tau=2$.
…arameters C at time (t-l). $\partial \psi(s_{t-l}) / \partial s_{t-l}$ is depended on $a_{t-l}$ and therefore on $C_{t-l}$.
Again, nothing changes for $\tau=2$.
scheunemann
commented
Nov 9, 2018
| @@ -316,11 +321,14 @@ void PiMax::learn(){ | |||
|
|
|||
| const Matrix& metric = useMetric ? gs.map(one_over).map(sqr) : gs.mapP(1, constant); | |||
|
|
|||
| C += ((( dmu * (ds[l]^T) - (epsrel & al) * (sl^T)) & metric) * epsCN | |||
There was a problem hiding this comment.
This line actually calculates the weights at time t rather then the delta. These total weights at time t then get passed for calculating the term for the next step, e.g, t-2.
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
Add this suggestion to a batch that can be applied as a single commit.
This suggestion is invalid because no changes were made to the code.
Suggestions cannot be applied while the pull request is closed.
Suggestions cannot be applied while viewing a subset of changes.
Only one suggestion per line can be applied in a batch.
Add this suggestion to a batch that can be applied as a single commit.
Applying suggestions on deleted lines is not supported.
You must change the existing code in this line in order to create a valid suggestion.
Outdated suggestions cannot be applied.
This suggestion has been applied or marked resolved.
Suggestions cannot be applied from pending reviews.
Suggestions cannot be applied on multi-line comments.
Suggestions cannot be applied while the pull request is queued to merge.
Suggestion cannot be applied right now. Please check back later.
I think the update order of the
a_bufferis off. For testing, I addedode_robots/simulations/humanoid-TiPIas from here and plugged in thepimaxfromselforg/controller.Always trigger
learn()(minor)I think it is beneficial that
step()always enterslearn()for ensuring that buffers like, e.g.,L_bufferget filled properly. Otherwise the data contained is not correct when swapping betweeneps[C|A] == 0andeps[C|A] > 0during runtime (I am actually doing this in my experiments). Done here.Filling
a_bufferI think after reading an adding sensor values to the buffer$a_t$ should be stored in the respective buffer. I added an assert here which fails in the original version.
s_buffer[t], learning should be triggered (learn()) and only thenConsidering the original equation before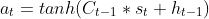
putting it after $t$ makes it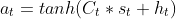 
and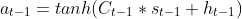 
for the next step. The assert won't fail.
learn(), e.g.,Matrix a = (C*(s_smooth) + h).map(g);with time indices, the value computed there waslearn()before increasingCaclulating the sum (A20/28)
For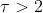
I think there are two issues related to the the sum (A20) or (28) in the special one-layer NN case. Firstly, the sum is meant to calculate 
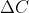but with adding 
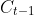what gets calculated is 
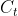. This 
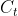then gets passed on to the calculation for, e.g., (t-2). I changed that in (694ab54) and left a comment.
I adapted the sum so
it's a bit tough to express everything in markdown with using these TeX-links. If you are interested I am happy to provide a PDF or have a chat over that. Also, I can make a PR with only the controller-changes if you prefer so.