Who would flardls bear?
Small amounts of Time spent waiting on downloads adds up over thousands over uses, both in human terms and in terms of energy usage. If we are to respond to the challenge of climate change, it's important to consider the efficiency and sustainability of computations we launch. Downloads may consume only a tiny fraction of cycles for computational science, but they often consume a noticeable fraction of wall-clock time.
While the download bit rate of one's local WAN link is the limit that matters most, downloading times are also governed by time spent waiting on handshaking to start transfers or to acknowledge data received. Synchronous downloads are highly energy-inefficient because hardware still consumes energy during waits. A more sustainable approach is to arrange the computational graph to do transfers simultaneously and asynchronously using multiple simultaneous downloads. The situation is made more complicated when downloads can be launched from anywhere in the world to a federated set of servers, possibly involving content delivery networks. Optimal download performance in that situation depends on adapting to network conditions and server loads, typically without no information other than the last download times of files.
Flardl downloads lists of files using an approach that adapts to local conditions and is elastic with respect to changes in network performance and server loads. Flardl achieves download rates typically more than 300X higher than synchronous utilities such as curl, while allowing use of multiple servers to provide superior protection against blacklisting. Download rates depend on network bandwidth, latencies, list length, file sizes, and HTTP protocol used, but using flardl, even a single server on another continent can usually saturate a gigabit cable connection after about 50 files.
Typically, one doesn't know much about the list of files to be downloaded, nor about the state of the servers one is going to use to download them. Once the first file request has been made to a given server, download software has only one means of control, whether to launch another download or wait. Making that decision well depends on making good guesses about likely return times.
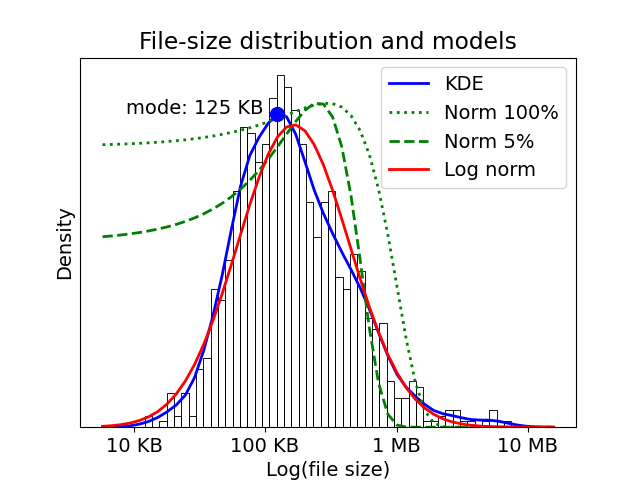
Collections of files generated by natural or human activity such as natural-language writing, protein structure determination, or genome sequencing tend to have size distributions with long tails. Such distributions have more big files than small files at a given size above or below the most-common (modal) size. Analytical forms of long-tail distributions include Zipf, power-law, and log-norm distributions. A real-world example of a long-tail distribution is shown below, which plots the file-size histogram for 1000 randomly-sampled CIF structure files from the Protein Data Bank, along with a kernel-density estimate and fits to log-normal and normal distributions.
Queueing algorithms that rely upon per-file rates as the pricipal control mechanism implicitly assume that queue statistics can be approximated with a normal-ish distribution, meaning one without a long tail. In making that assumption, they largely ignore the effects of big files on overall download statistics. Such algorithms inevitably encounter problems because mean values are neither stable nor characteristic of the distribution. For example, as can be seen in the fits above, the mean and standard distribution of samples drawn from a long-tail distribution tend to grow with increasing sample size. The fit of a normal distribution to a sample of 5% of the data (dashed line) gives a markedly lower mean and standard deviation than the fit to all points (dotted line), and both fits are poor. The mean tends to grow with sample size because larger samples are more likely to include a huge file that dominates the average value.
Algorithms that employ average per-file rates or times as the
primary means of control will launch requests too slowly most
of the time while letting queues run too deep when big downloads
are encountered. While the mean per-file download time isn't a
good statistic, control based on modal per-file file statistics
can be more consistent. For example, the modal per-file download
time
At first glance, running at high queue depths seems attractive. One of the simplest queueing algorithms would to simply put every job in a queue at startup and let the server(s) handle requests in parallel up to their individual critical queue depths, above which depths they are responsible for serialization . But such non-adaptive non-elastic algorithms give poor real-world performance or multiple reasons. First, if there is more than one server queue, differing file sizes and transfer rates will result in the queueing equivalent of Amdahl's law, by creating an overhang where one server still has multiple files queued up to serve while others have completed all requests. The server with the overhang is also not guaranteed to be the fastest one.
If a server decides you are abusing its queue policies, it may take action that hurts your current and future downloads. Most public-facing servers have policies to recognize and defend against Denial-Of-Service (DOS) attacks and a large number of requests from a single IP address in a short time is the main hallmark of a DOS attack. The minimal response to a DOS event causes the server to dump your latest requests, a minor nuisance. Worse is if the server responds by severely throttling further requests from your IP address for hours or sometime days. But in the worst case, your IP address can get the "death penalty" of being put on a permanent blacklist for throttling or blockage that may require manual intervention by someone in control of the server to get removed from. Blacklisting might not even be your personal fault, but a collective problem. I have seen a practical class of 20 students brought to a complete halt by a 24-hour blacklisting of the institution's public IP address by a government site. Until methods are developed for servers to publish their "play-friendly" values and to whitelist known-friendly clients, the highest priority for downloading algorithms must be to avoid blacklisting by a server by minimizing queue depth. At the other extreme, the absolute minimum queue depth is retreating back to synchronous downloading. How can we balance the competing demands of speed while avoiding blacklisting?
An analogy might help us here. Let's say you are a person who enjoys keeping track of statistics, and you decide to try fishing. At first, you have a single fishing rod and you go fishing at a series of local lakes where your catch consists of small fishes called "crappies". Your records reval that while the rate of catching fishes can vary from day to day--fish might be hungry or not--the average size of a crappie from a given pond is pretty stable. Bigger ponds tend to have bigger crappies in them, and it might take slightly longer to reel in a bigger crappie than a small one, but the rate of catching crappies averages out pretty quickly.
You love fishing so much that one day you drive to the coast and charter a fishing boat. On that boat, you can set out as many lines as you want (up to some limit) and fish in parallel. At first, you catch mostly small fishes that are the ocean-going equivalent of crappies. But eventually you hook a small whale. Not does it take a lot of your time and attention to reel in the whale, but landing it totally skews the average weight and catch rate. You and your crew can only effecively reel in so many hooked lines at once. Putting out more lines than that effective limit of hooked plus waiting-to-be-hooked lines only results in more wait times in the ocean.
Our theory of fishing says to put out lines at the usual rate of catching crappies but limit the number of lines to deal with whales. The most probable rate of catching modal-sized fies will be optimistic, but you can delay putting out more lines if you reach the maximum number of lines your boat can handle. Once you catch enough to be able to estimate how fish are biting, you can back off the number of lines to the number that you and your crew can handle at a time that day.
Flardl implements a method I call "adaptilastic" queueing to deliver robust performance in real situations. Adaptilastic queueing uses timing on transfers from an initial period—launched using optimistic assumptions—to optimize later transfers by using the minimum total depth over all quese that will saturate the download bit rate while avoiding excess queue depth on any given server. Flardl distinguishes among four different operating regimes in selecting the per-server launch rates:
- Naive, where no transfers have ever been completed, launch at a rate which assumes the maximum bandwidth will be achieved with a modal-sized file at this launch (so that launches get slower with the total queue depth).
- Informed, where information from a previous run is available, launch at the previous modal service rate for this server, adjusted upwards for the maximum bandwidth.
- Arriving, where information from at least one transfer to at least one server has occurred but not enough to fully characterize the server connection, send out at the average file return rate (since the first files are not whales).
- Updated, where a sufficient number of transfers has occurred that file transfers may be characterized, send out at the modal file rate for this server.
After waiting an exponentially-distributed stochastic period given by the applicable per-server launch rate, testing is done against four limits:
- The per-server queue depth must be less than the maximum
$D_{{\rm max}_j}$ , an input parameter revised downward if any queue requests are rejected, - The curremt download bit rate must be less than
$B_{\rm max}$ , the maximum bandwidth allowed. - In the updated state with per-server stats available, the
per-server queue depth must be less than the calculated critical
per-server queue depth
$D_{{\rm crit}_j}$ , as discussed in the theoretical section. - In the updated state, the total queue depth must be less than
the saturation queue depth,
$D_{\rm sat}$ , at which the current download bit rate$B_{\rm cur}$ saturates, as calculated in the theoretical section.
If any of the limits are exceeded, a stochastic wait period
at the inverse of the current per-server rate
The adapilastic algorithm assumes that file sizes are randomly-ordered
in the list. But what if we know the file sizes beforehand? The server
that draws the biggest file is most likely to finish last, so it's
important for that file to be started on the lowest-latency server as
soon as one has current information about which server is indeed
fastest (i.e., by reaching the arriving state). The way that flardl
optimizes downloads when provided a dictionary of relative file sizes
is to sort the incoming list of downloads into two lists. The first
list (the crappies list) is sorted into tiers of files with the size
of the tier equal to the number of servers
Flardl is tested under the highest supported python version on Linux, MacOS, and Windows and under the lowest supported python version on Linux. Under the hood, flardl relies on httpx and is supported on whatever platforms that library works for both HTTP/1.1 and HTTP/2.
You can install Flardl via pip from PyPI:
$ pip install flardlFlardl has no CLI and does no I/O other than downloading. Writing files and logging is done in user-provided code. See test examples for usage.
Contributions are very welcome. To learn more, see the Contributor Guide.
Distributed under the terms of the BSD 3-clause license, flardl is free and open source software.
If you encounter any problems, please file an issue along with a detailed description.
Flardl was written by Joel Berendzen.