Optimized Kalman Filter

Summary

This repo implements an Optimized Kalman Filter (OKF), which optimizes the parameters $Q,R$ to minimize the MSE.

Motivation: The KF parameters $Q,R$ are usually estimated as the covariances of the noise. However, such estimation is usually sub-optimal, hence explicit MSE optimization is preferable, as discussed in the NeurIPS 2023 paper Optimization or Architecture: How to Hack Kalman Filtering, by Ido Greenberg, Netanel Yannay and Shie Mannor.

Problem setup: A dataset of trajectories is required, with both observations and true system-states (learning from observations alone is currently not supported). The parameters $Q,R$ are optimized with respect to this dataset, and then can be used to make predictions on new trajectories.

Installation: pip install Optimized-Kalman-Filter

Usage example: example.ipynb.

• Background
• When to use
• Why to use
• How to use
• Cite us

The standard KF (tuned by noise-estimation) vs. the Optimized KF, in the test data of the simple-lidar example problem: errors summary (left) and a sample of models predictions against the actual target (right) (images from example.ipynb)

Background: the Kalman Filter

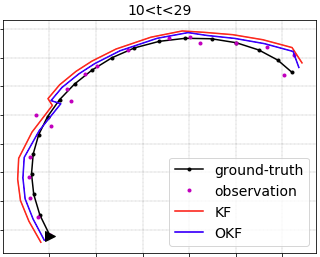
The Kalman Filter (KF) is a popular algorithm for filtering problems such as state estimation, smoothing, tracking and navigation. For example, consider tracking a plane using noisy measurements (observations) from a radar. Every time-step, we try to predict the motion of the plane, then receive a new measurement from the radar and update our belief accordingly.

An illustration of a single step of the Kalman Filter: predict the next state (black arrow); receive a new observation (green ellipse); update your belief about the state (mixing the two right ellipses) (image by Ido Greenberg)

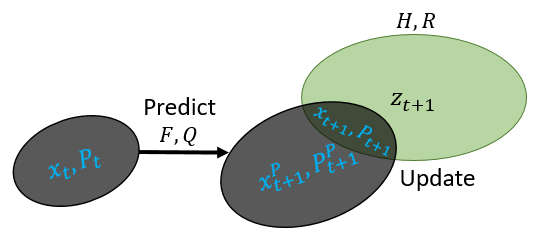
A diagram of the Kalman Filter algorithm (image by Ido Greenberg)

To tune the KF, one has to determine the parameters representing the measurement (observation) noise and the motion-prediction noise, expressed as covariance matrices R and Q. Given a dataset of measurements {z_t} (e.g. from the radar), tuning these parameters may be a difficult task, and has been studied for many decades. However, given data of both measurements {z_t} and true-states {x_t} (e.g. true plane locations), the parameters R,Q are usually estimated from the data as the sample covariance matrices of the noise.

When to use this package

When you want to build a Kalman Filter for your problem, and you have a training dataset with sequences of both states {x_t} and observations {z_t}.

Why to use

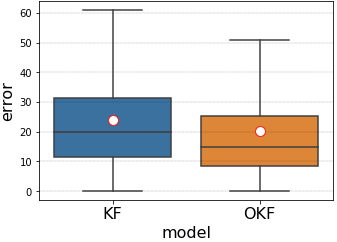
Tuning the KF parameters through noise estimation (as explained above) yields optimal model predictions - under the KF assumptions. However, as shown in the paper, whenever the assumptions do not hold, optimization of the parameters may lead to more accurate predictions. Since most practical problems do not satisfy the assumptions, and since assumptions violations are often not noticed at all by the user, optimization of the parameters is a good practice whenever a corresponding dataset is available.

How to use

Installation: pip install Optimized-Kalman-Filter

Import: import okf

Usage example: example.ipynb.

Data

The data consists of 2 lists of length n, where n is the number of trajectories in the data:

1. X[i] = a numpy array of type double and shape (n_time_steps(trajectory i), state_dimension).
2. Z[i] = a numpy array of type double and shape (n_time_steps(trajectory i), observation_dimension).

For example, if a state is 4-dimensional (e.g. (x,y,vx,vy)) and an observation is 2-dimensional (e.g. (x,y)), and the i'th trajectory has 30 time-steps, then X[i].shape is (30,4) and Z[i].shape is (30,2).

Below we assume that Xtrain, Ztrain, Xtest, Ztest correspond to train and test datasets of the format specified above.

KF configuration

The configuration of the KF has to be specified as a dict model_args containing the following entries:

• dim_x: the number of entries in a state
• dim_z: the number of entries in an observation
• F: the dynamics model: a pytorch tensor of type double and shape (dim_x, dim_x)
• H: the observation model: a pytorch tensor of type double and shape (dim_z, dim_x); or a function that returns such a tensor given the estimated state and the current observation
• loss_fun: function(predicted_x, true_x) used as loss for training and evaluation
• State initialization: initialize either explicitly via x0 (tensor of shape dim_x); or from the first observation via the function init_z2x

See an example here.

Train and test

import okf
model = okf.OKF(**model_args)  # set optimize=False for the standard KF baseline
okf.train(model, Ztrain, Xtrain)
loss = okf.test_model(model, Ztest, Xtest, loss_fun=model_args['loss_fun'])

Analysis

See example.ipynb.

Cite us

@article{greenberg2023okf,
  title={Optimization or architecture: how to hack Kalman filtering},
  author={Greenberg, Ido and Yannay, Netanel and Mannor, Shie},
  journal={Advances in Neural Information Processing Systems},
  year={2023}
}