Definition of the SAT decision problem:
Given predicate P in Conjunctive Normal Form (CNF), is P satisfiable?
sat decides instances of SAT. Furthermore, for each input predicate P found to be in SAT, it calculates all satisfying assignments of P's variables.
SAT is an NP-complete problem. A trivial algorithm for solving an instance of SAT is to enumerate all possible assignments to its variables and to test each assignment for satisfaction of the predicate.
The solution to the SAT problem provided by the sat application is based on this algorithm.
The solution is based on Hui-Hsien Chou and James A. Reggia's article: Problem solving during artificial selection of self-replicating loops, in which they show how to encode a SAT problem instance as a set of rules for self-replicating loops in a cellular automata space.
In Chou and Reggia's paper, the solution discussed is for the K-SAT problem (where each clause in the CNF predicate is of a constant length: K). The sat application extends the solution to solving any instance of SAT. It also supports CNF expressions with clauses in which there are multiple instances of one or more variables.
Each loop is replicated with a slight mutation whereby it either becomes a representation for some possible assignment for the SAT instance or it replicates on so as to create such representations.
The replication rules are constructed such that loops representing non-satisfying assignments are removed from the cellular space and indeed - may not even be created at all. Ultimately, only loops containing a satisfying representation of the SAT instance - if such exist - will prevail.
The sat application uses an event loop to provide a multi tasked single threaded environment. The implementation of the cellular space differs slightly from the classic definition of CA space in that it is event driven. That is, most cells are in a dormant state and are not active during iteration. Only cells on the loops, or on the extensions of replicating loops are active and change their state from iteration to iteration.
The following example shows different stages (iterations) during the calculation of the SAT problem:
P = (l1 or o2 or l3) and (-l1 or l2) and (l2 or l3) and (-l3 or l1)
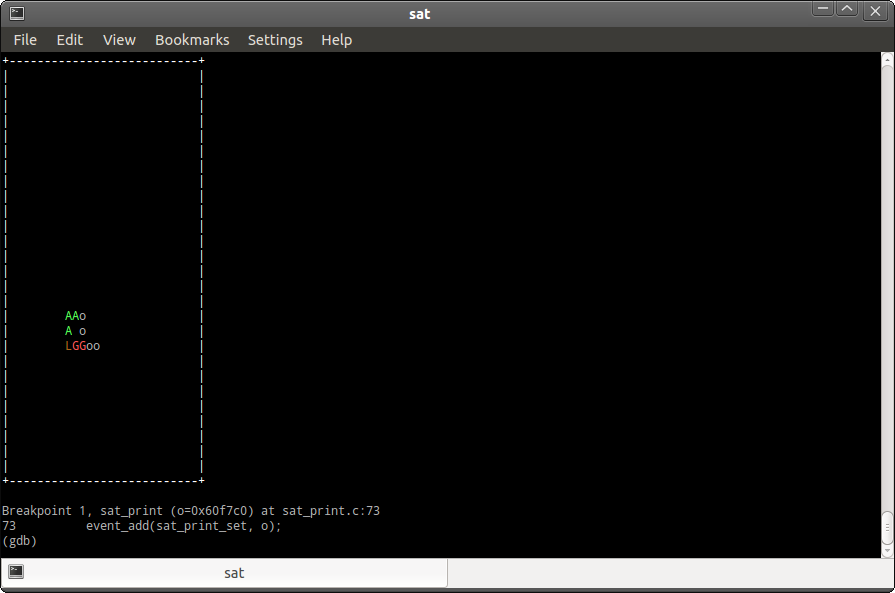
The initial cellular automata field configuration
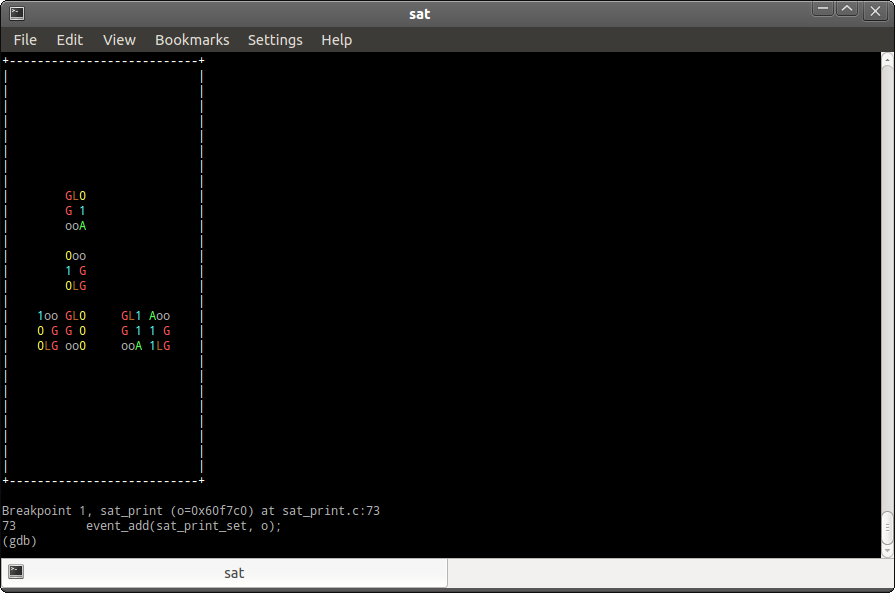
The cellular automata space after 125 iterations:
Some loops carry potentially satisfying assignments and some carry fully explored assignments
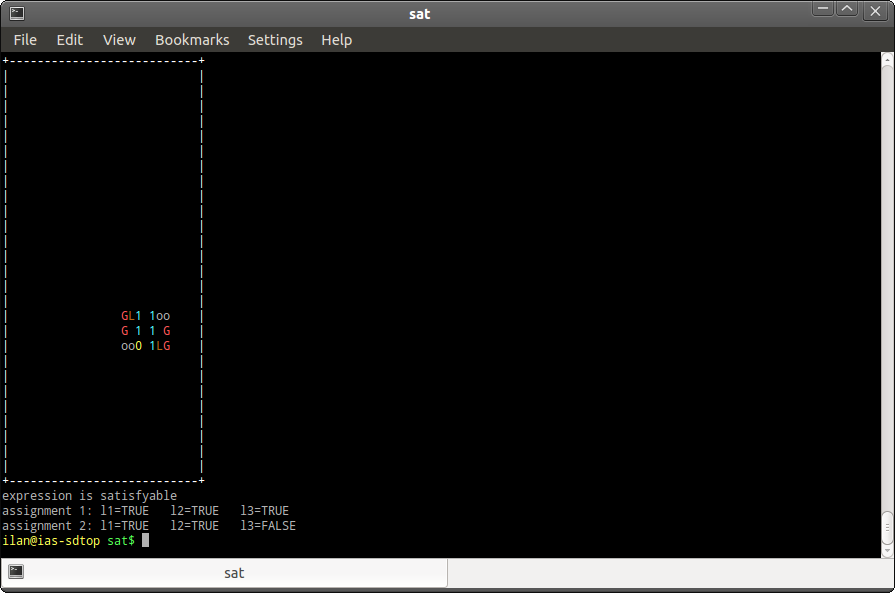
The final configuration:
Two loops have survived and they represent the two satisfying assignments that exist for P