Diffusion model in web browser

Online Demo! Run it in your web browser

• 第一集: https://www.bilibili.com/video/BV1tz4y1h7q1 | 正态分布 | 基本设定 | 公式推导 |
• 第二集: https://www.bilibili.com/video/BV1xQ4y1w7ex | 神经网络 | 概率空间 | 边缘概率 | 各向同性高斯分布 |
• 第三集: https://www.bilibili.com/video/BV1hZ421y7id | 三维动画展示全过程
• 第四集: https://www.bilibili.com/video/BV1gK421b7W9 | 神经网络的学习目标以及训练
• 第五集: https://www.bilibili.com/video/BV12y421z7Mh/ | 花絮 | 热度图制作细节揭秘

Youtube

UPDATE:

• 2024-07-14 : Update online sample to use WebGPU if possible
• 2024-07-15 : Added DDIM sampling method

---

1. DDPM Introduction

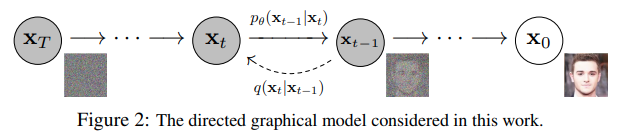
• $q$ - a fixed (or predefined) forward diffusion process of adding Gaussian noise to an image gradually, until ending up with pure noise
• $p_θ$ - a learned reverse denoising diffusion process, where a neural network is trained to gradually denoise an image starting from pure noise, until ending up with an actual image.

Both the forward and reverse process indexed by $t$ happen for some number of finite time steps $T$ (the DDPM authors use $T$=1000). You start with $t=0$ where you sample a real image $x_0$ from your data distribution, and the forward process samples some noise from a Gaussian distribution at each time step $t$, which is added to the image of the previous time step. Given a sufficiently large $T$ and a well behaved schedule for adding noise at each time step, you end up with what is called an isotropic Gaussian distribution at $t=T$ via a gradual process

2. Forward Process $q$

$$ x_0 \overset{q(x_1 | x_0)}{\rightarrow} x_1 \overset{q(x_2 | x_1)}{\rightarrow} x_2 \rightarrow \dots \rightarrow x_{T-1} \overset{q(x_{t} | x_{t-1})}{\rightarrow} x_T $$

This process is a markov chain, $x_t$ only depends on $x_{t-1}$. $q(x_{t} | x_{t-1})$ adds Gaussian noise at each time step $t$, according to a known variance schedule $β_{t}$

$$ x_t = \sqrt{1-β_t}\times x_{t-1} + \sqrt{β_t}\times \epsilon_{t} $$

• $β_t$ is not constant at each time step $t$. In fact one defines a so-called "variance schedule", which can be linear, quadratic, cosine, etc.

$$ 0 < β_1 < β_2 < β_3 < \dots < β_T < 1 $$

• $\epsilon_{t}$ Gaussian noise, sampled from standard normal distribution.

$$ x_t = \sqrt{1-β_t}\times x_{t-1} + \sqrt{β_t} \times \epsilon_{t} $$

Define $a_t = 1 - β_t$

$$ x_t = \sqrt{a_{t}}\times x_{t-1} + \sqrt{1-a_t} \times \epsilon_{t} $$

2.1 Relationship between $x_t$ and $x_{t-2}$

$$ x_{t-1} = \sqrt{a_{t-1}}\times x_{t-2} + \sqrt{1-a_{t-1}} \times \epsilon_{t-1}$$

$$ \Downarrow $$

$$ x_t = \sqrt{a_{t}} (\sqrt{a_{t-1}}\times x_{t-2} + \sqrt{1-a_{t-1}} \epsilon_{t-1}) + \sqrt{1-a_t} \times \epsilon_t $$

$$ \Downarrow $$

$$ x_t = \sqrt{a_{t}a_{t-1}}\times x_{t-2} + \sqrt{a_{t}(1-a_{t-1})} \epsilon_{t-1} + \sqrt{1-a_t} \times \epsilon_t $$

Because $N(\mu_{1},\sigma_{1}^{2}) + N(\mu_{2},\sigma_{2}^{2}) = N(\mu_{1}+\mu_{2},\sigma_{1}^{2} + \sigma_{2}^{2})$

Proof

$$ x_t = \sqrt{a_{t}a_{t-1}}\times x_{t-2} + \sqrt{a_{t}(1-a_{t-1}) + 1-a_t} \times \epsilon $$

$$ \Downarrow $$

$$ x_t = \sqrt{a_{t}a_{t-1}}\times x_{t-2} + \sqrt{1-a_{t}a_{t-1}} \times \epsilon $$

2.2 Relationship between $x_t$ and $x_{t-3}$

$$ x_{t-2} = \sqrt{a_{t-2}}\times x_{t-3} + \sqrt{1-a_{t-2}} \times \epsilon_{t-2} $$

$$ \Downarrow $$

$$ x_t = \sqrt{a_{t}a_{t-1}}(\sqrt{a_{t-2}}\times x_{t-3} + \sqrt{1-a_{t-2}} \epsilon_{t-2}) + \sqrt{1-a_{t}a_{t-1}}\times \epsilon $$

$$ \Downarrow $$

$$ x_t = \sqrt{a_{t}a_{t-1}a_{t-2}}\times x_{t-3} + \sqrt{a_{t}a_{t-1}(1-a_{t-2})} \epsilon_{t-2} + \sqrt{1-a_{t}a_{t-1}}\times \epsilon $$

$$ \Downarrow $$

$$ x_t = \sqrt{a_{t}a_{t-1}a_{t-2}}\times x_{t-3} + \sqrt{a_{t}a_{t-1}-a_{t}a_{t-1}a_{t-2}} \epsilon_{t-2} + \sqrt{1-a_{t}a_{t-1}}\times \epsilon $$

$$ \Downarrow $$

$$ x_t = \sqrt{a_{t}a_{t-1}a_{t-2}}\times x_{t-3} + \sqrt{(a_{t}a_{t-1}-a_{t}a_{t-1}a_{t-2}) + 1-a_{t}a_{t-1}} \times \epsilon $$

$$ \Downarrow $$

$$ x_t = \sqrt{a_{t}a_{t-1}a_{t-2}}\times x_{t-3} + \sqrt{1-a_{t}a_{t-1}a_{t-2}} \times \epsilon $$

2.3 Relationship between $x_t$ and $x_0$

• $x_t = \sqrt{a_{t}a_{t-1}}\times x_{t-2} + \sqrt{1-a_{t}a_{t-1}}\times \epsilon$
• $x_t = \sqrt{a_{t}a_{t-1}a_{t-2}}\times x_{t-3} + \sqrt{1-a_{t}a_{t-1}a_{t-2}}\times \epsilon$
• $x_t = \sqrt{a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{t-(k-2)}a_{t-(k-1)}}\times x_{t-k} + \sqrt{1-a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{t-(k-2)}a_{t-(k-1)}}\times \epsilon$
• $x_t = \sqrt{a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{2}a_{1}}\times x_{0} + \sqrt{1-a_{t}a_{t-1}a_{t-2}a_{t-3}...a_{2}a_{1}}\times \epsilon$

$$\bar{a}{t} := a{t}a_{t-1}a_{t-2}a_{t-3}...a_{2}a_{1}$$

$$x_{t} = \sqrt{\bar{a}_t}\times x_0+ \sqrt{1-\bar{a}_t}\times \epsilon , \epsilon \sim N(0,I) $$

$$ \Downarrow $$

$$ q(x_{t}|x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-\bar{a}_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) } $$

3.Reverse Process $p$

Because $P(A|B) = \frac{ P(B|A)P(A) }{ P(B) }$

$$ p(x_{t-1}|x_{t},x_{0}) = \frac{ q(x_{t}|x_{t-1},x_{0})\times q(x_{t-1}|x_0)}{q(x_{t}|x_0)} $$

$$x_{t} = \sqrt{a_t}x_{t-1}+\sqrt{1-a_t}\times ϵ$$	~	$N(\sqrt{a_t}x_{t-1}, 1-a_{t})$
$$x_{t-1} = \sqrt{\bar{a}_{t-1}}x_0+ \sqrt{1-\bar{a}_{t-1}}\times ϵ$$	~	$N( \sqrt{\bar{a}_{t-1}}x_0, 1-\bar{a}_{t-1})$
$$x_{t} = \sqrt{\bar{a}_{t}}x_0+ \sqrt{1-\bar{a}_{t}}\times ϵ$$	~	$N( \sqrt{\bar{a}_{t}}x_0, 1-\bar{a}_{t})$

$$ q(x_{t}|x_{t-1},x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-a_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_{t}} \right ) } $$

$$ q(x_{t-1}|x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-\bar{a}_{t-1}}} e^{\left ( -\frac{1}{2}\frac{(x_{t-1}-\sqrt{\bar{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} \right ) } $$

$$ q(x_{t}|x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-\bar{a}_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) } $$

$$ \frac{ q(x_{t}|x_{t-1},x_{0})\times q(x_{t-1}|x_0)}{q(x_{t}|x_0)} = \left [ \frac{1}{\sqrt{2\pi} \sqrt{1-a_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_{t}} \right ) } \right ] * \left [ \frac{1}{\sqrt{2\pi} \sqrt{1-\bar{a}_{t-1}}} e^{\left ( -\frac{1}{2}\frac{(x_{t-1}-\sqrt{\bar{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} \right ) } \right ] \div \left [ \frac{1}{\sqrt{2\pi} \sqrt{1-\bar{a}_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) } \right ] $$

$$ \Downarrow $$

$$ \frac{\sqrt{2\pi} \sqrt{1-\bar{a}_{t}}}{\sqrt{2\pi} \sqrt{1-a_{t}} \sqrt{2\pi} \sqrt{1-\bar{a}_{t-1}} } e^{\left [ -\frac{1}{2} \left ( \frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_{t}} + \frac{(x_{t-1}-\sqrt{\bar{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) \right]} $$

$$ \Downarrow $$

$$\frac{1}{\sqrt{2\pi} \left( \frac{\sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}}}{\sqrt{1-\bar{a}_{t}}} \right)} \exp \left[ -\frac{1}{2} \left( \frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_t} + \frac{(x_{t-1}-\sqrt{\bar{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right) \right] $$

$$ \Downarrow $$

$$ \frac{1}{\sqrt{2\pi} \left( \frac{\sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}}}{\sqrt{1-\bar{a}_{t}}} \right)} \exp \left[ -\frac{1}{2} \left ( \frac{ x_{t}^2-2\sqrt{a_t}x_{t}x_{t-1}+{a_t}x_{t-1}^2 }{1-a_t} + \frac{ x_{t-1}^2-2\sqrt{\bar{a}_{t-1}}x_0x_{t-1}+\bar{a}_{t-1}x_0^2 }{1-\bar{a}_{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right) \right] $$

$$ \Downarrow $$

$$\frac{1}{\sqrt{2\pi} \left( \frac{\sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}}}{\sqrt{1-\bar{a}_{t}}} \right)} \exp \left[ -\frac{1}{2} \frac{ \left( x_{t-1} - \left( \frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t}x_t + \frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t}x_0 \right) \right)^2 }{ \left( \frac{\sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}}}{\sqrt{1-\bar{a}_{t}}} \right)^2 } \right]$$

$$ \Downarrow $$

$$ p(x_{t-1}|x_{t}) \sim N\left( \frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t}x_t + \frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t}x_0, \left( \frac{\sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}}}{\sqrt{1-\bar{a}_{t}}} \right)^2 \right) $$

Because $x_{t} = \sqrt{\bar{a}_t}\times x_0+ \sqrt{1-\bar{a}_t}\times \epsilon$, $x_0 = \frac{x_t - \sqrt{1-\bar{a}_t}\times \epsilon}{\sqrt{\bar{a}_t}}$. Substitute $x_0$ with this formula.

$$ p(x_{t-1}|x_{t}) \sim N\left( \frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t}x_t + \frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t}\times \frac{x_t - \sqrt{1-\bar{a}_t}\times \epsilon}{\sqrt{\bar{a}_t}}, \frac{\beta_{t} (1-\bar{a}_{t-1})}{1-\bar{a}_{t}} \right) $$

$$ p(x_{t-1}|x_{t}) \sim N\left( \frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t}x_t + \frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t}\times \frac{x_t - \sqrt{1-\bar{a}_t}\times \epsilon}{\sqrt{\bar{a}_t}}, \frac{\beta_{t} (1-\bar{a}_{t-1})}{1-\bar{a}_{t}} \right) $$

Note: This README.md is intended solely for previewing on the Github page. If you wish to view the rendered page locally, please consult README.raw.md.