Advanced Monte Carlo sampling and model fitting of various exotic option data to various market models.
See docs/main.pdf for more info.
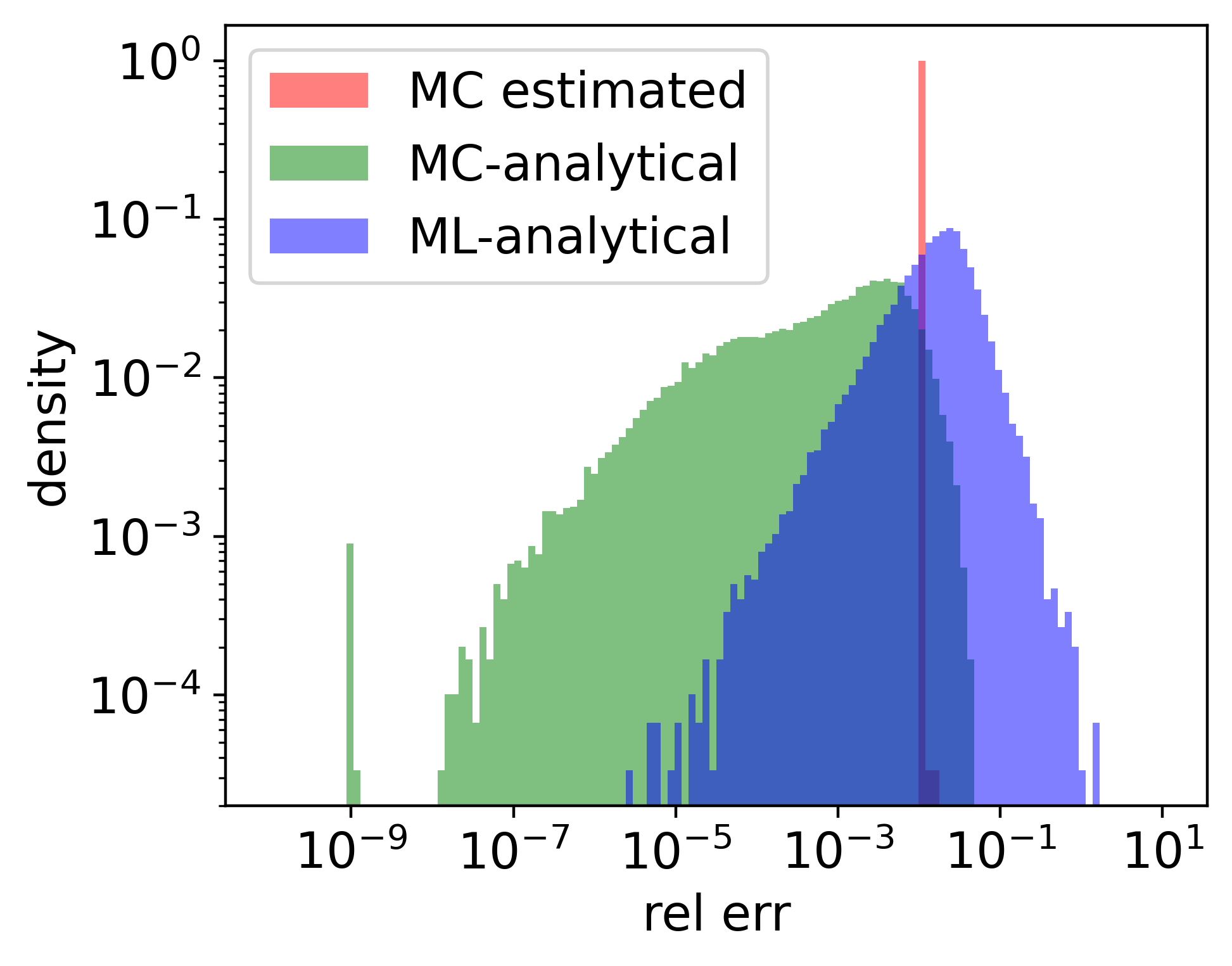
Some early results of nonlinear fitting via deep neural networks (340 params), for much faster pricing. Monte-Carlo integrator estimated relative error target is set to 1% (red). Actual relative error is highly controlled (green), exceeding the target with exponentially vanishing probability. Actual relative error of deep neural network contains many more outliers, but mean is ~2%. Main limitations:
- The MC integration is pure MC, so
$n^{-1/2}$ scaling. Switch to randomized quasi-Monte Carlo integration. But this requires dimensionality reduction due to the path-dependent stochastic processes, so Brownian bridge sampling. Asymptotically better convergence will allow higher quality data, part of the ML bottleneck. - Adjust statistical distribution of model and option parameters away from uniform, to produce more of the samples the DNN struggles with.
- Improve the somewhat simplistic model, and hyperparameter optimization.
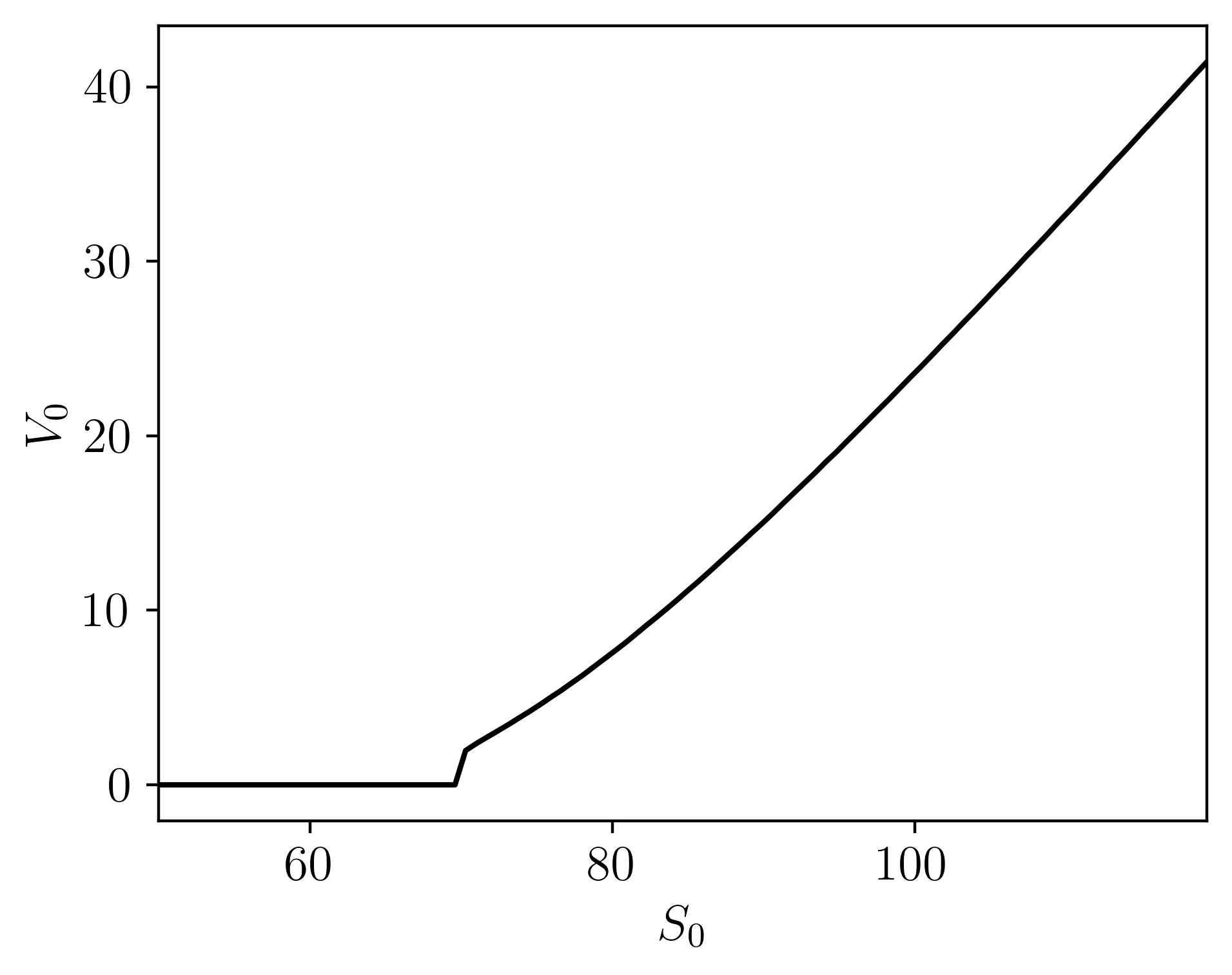
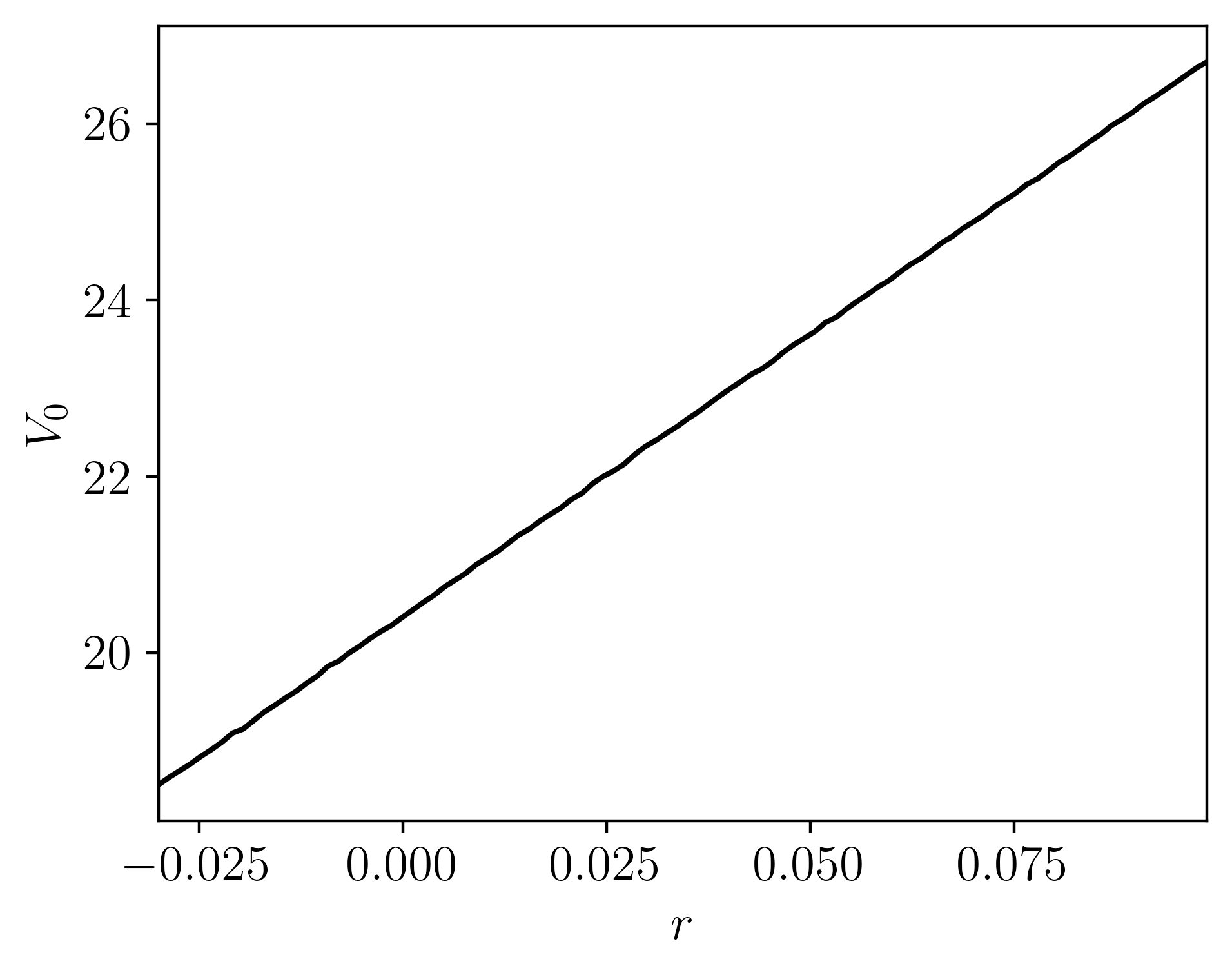
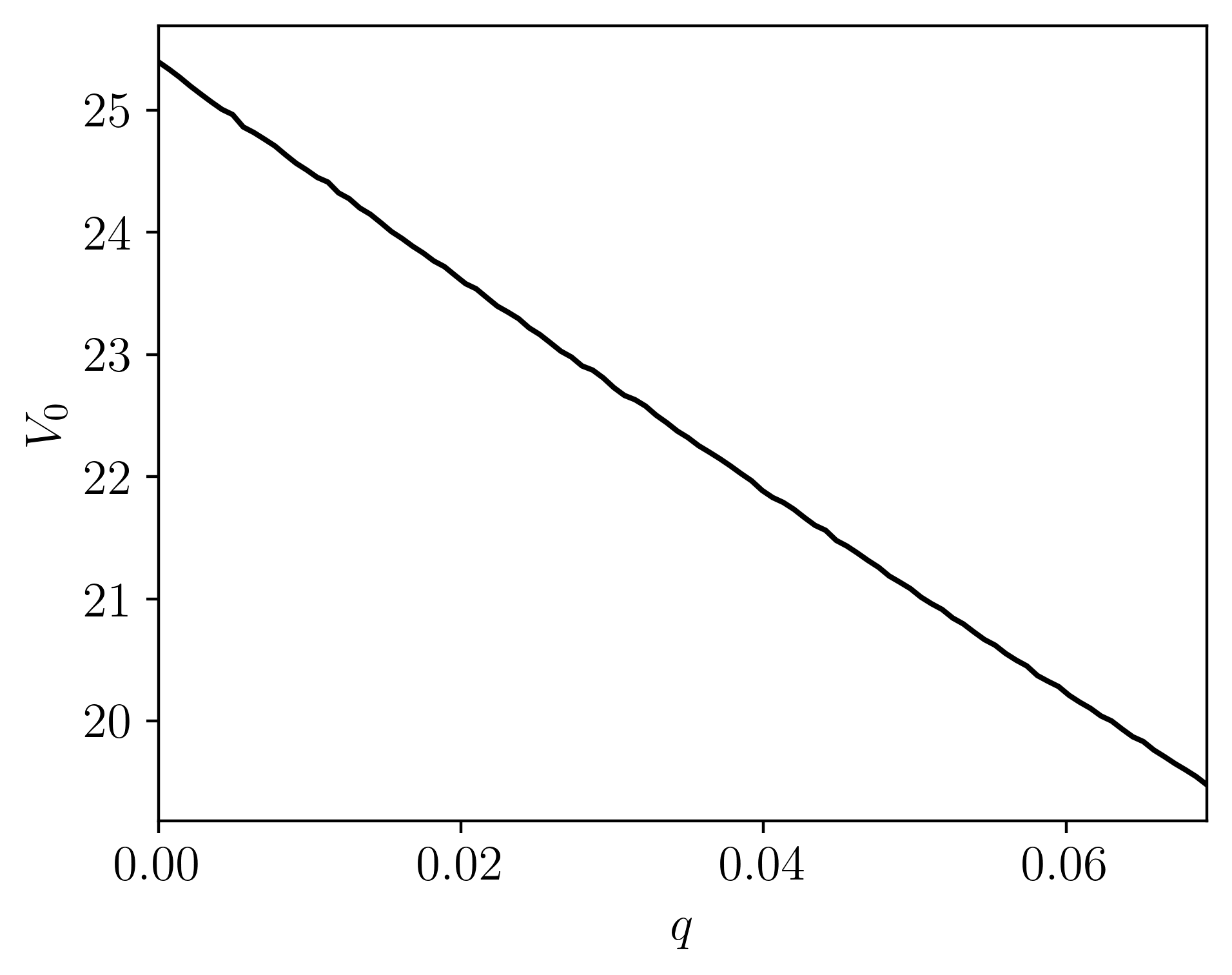
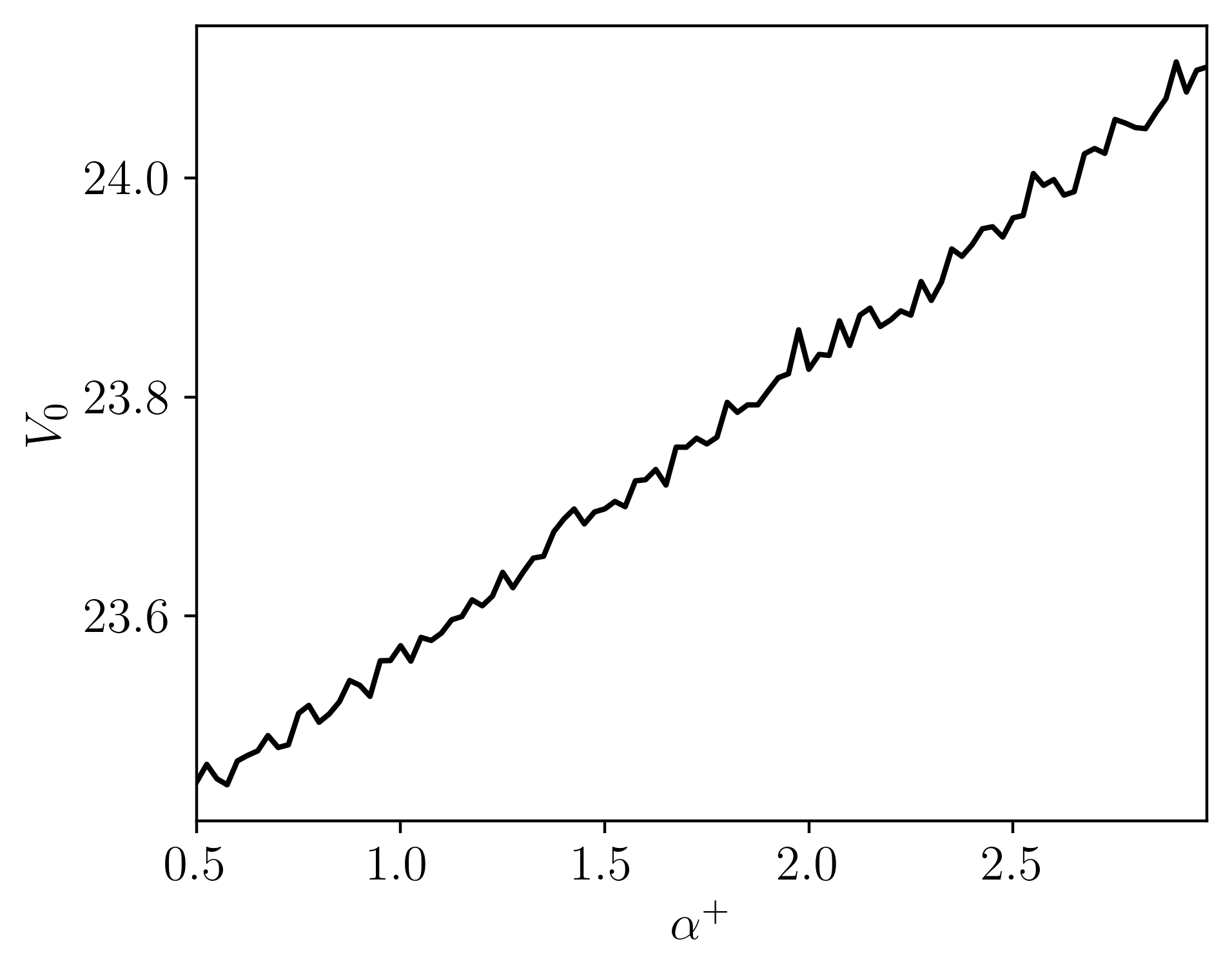
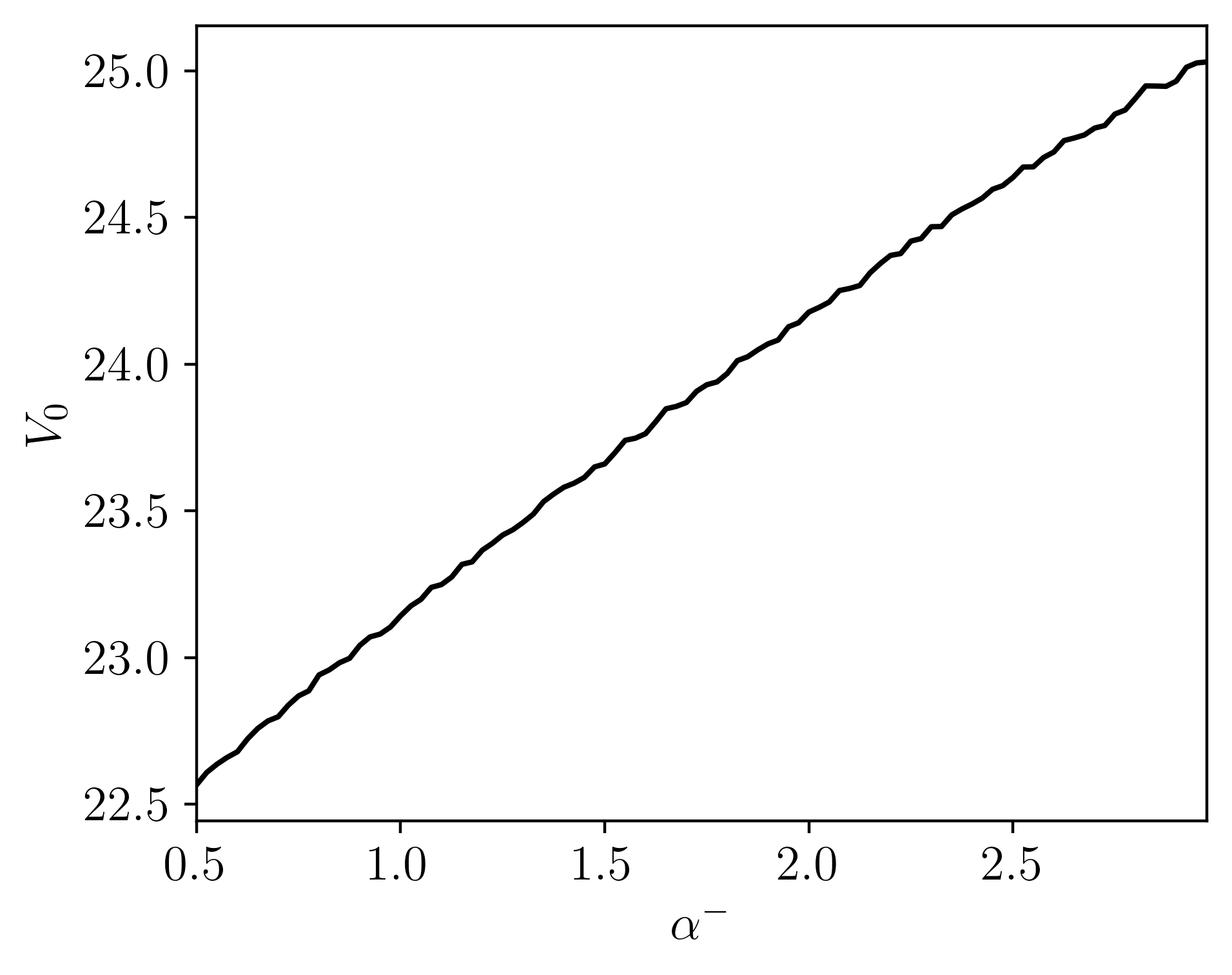
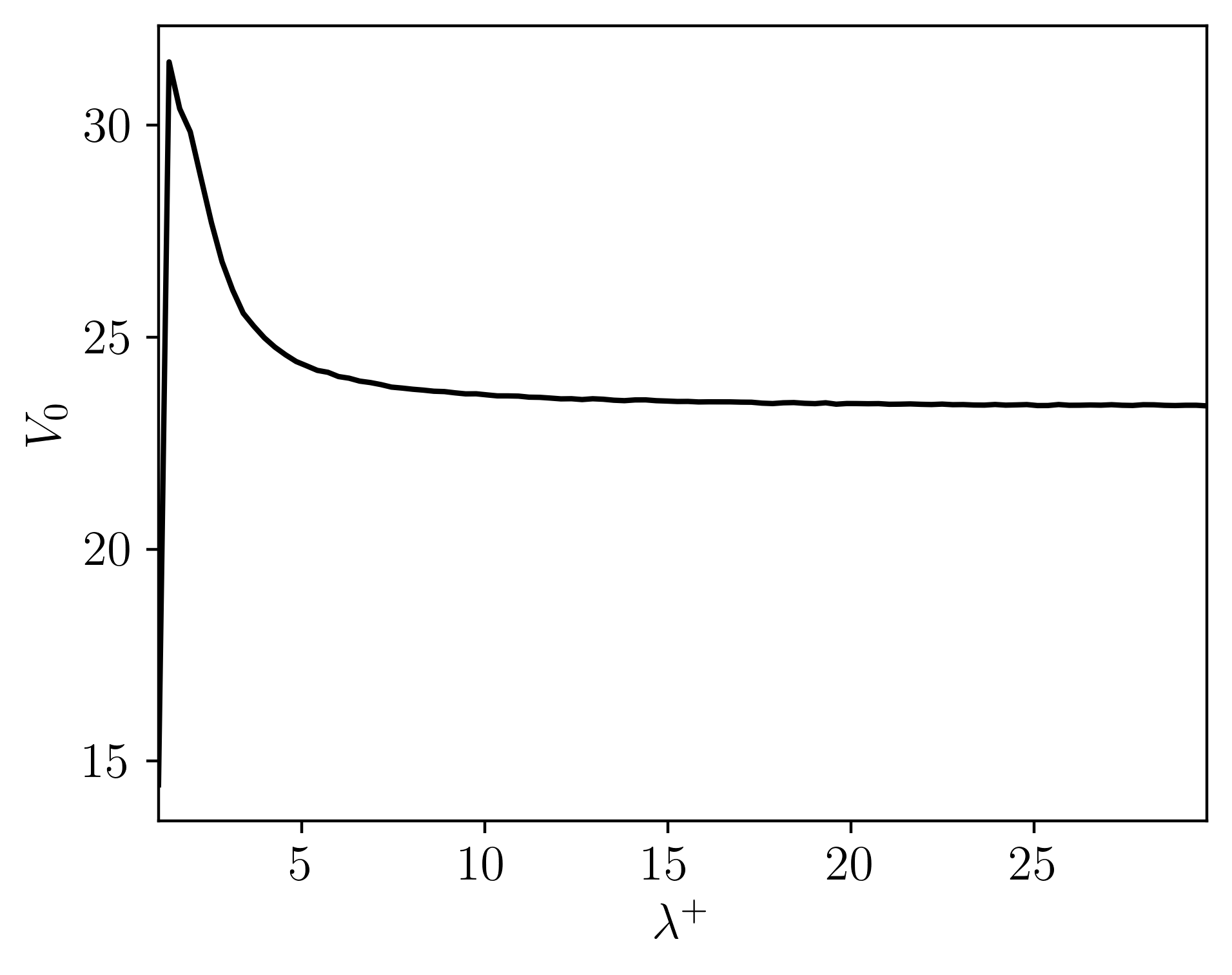
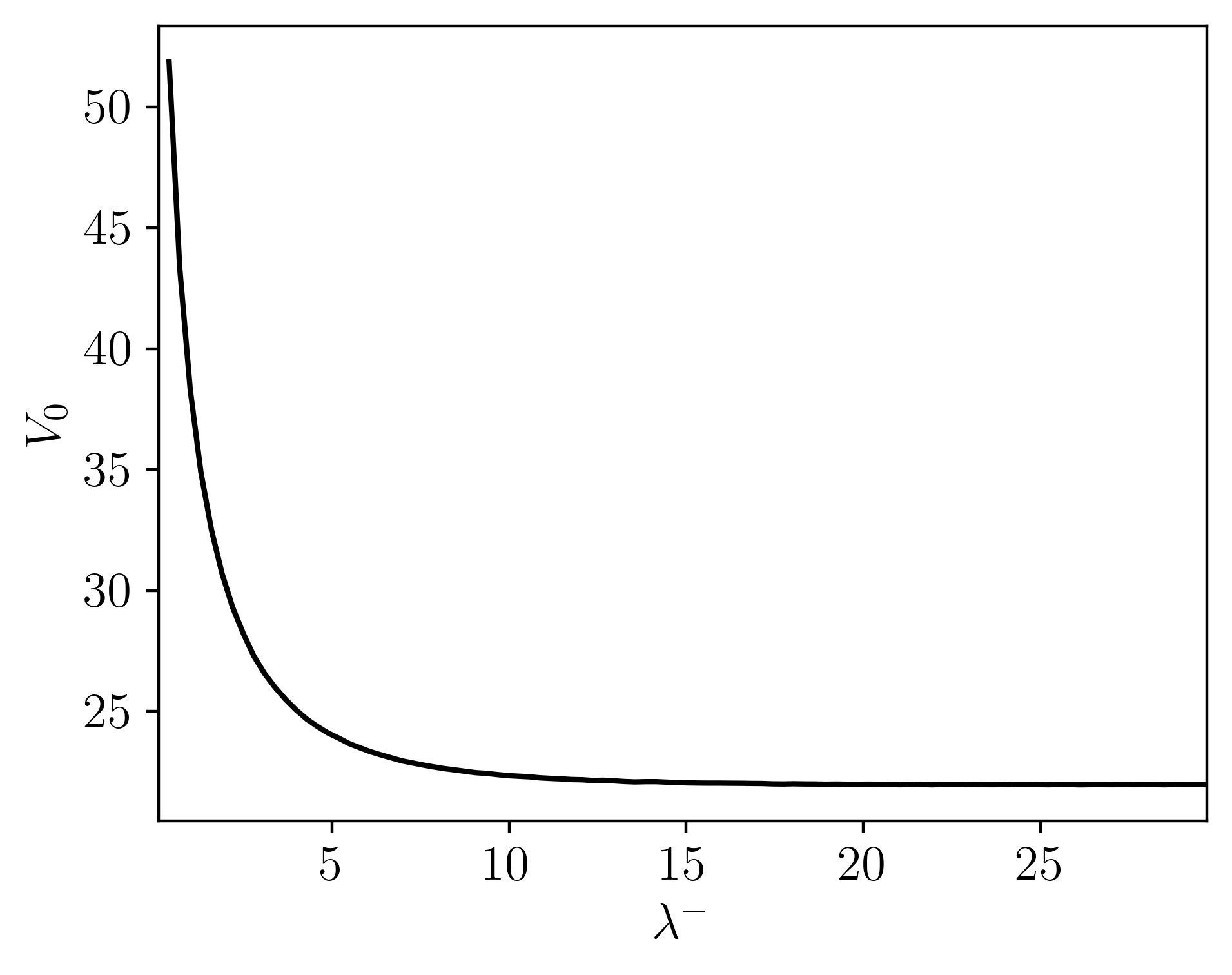
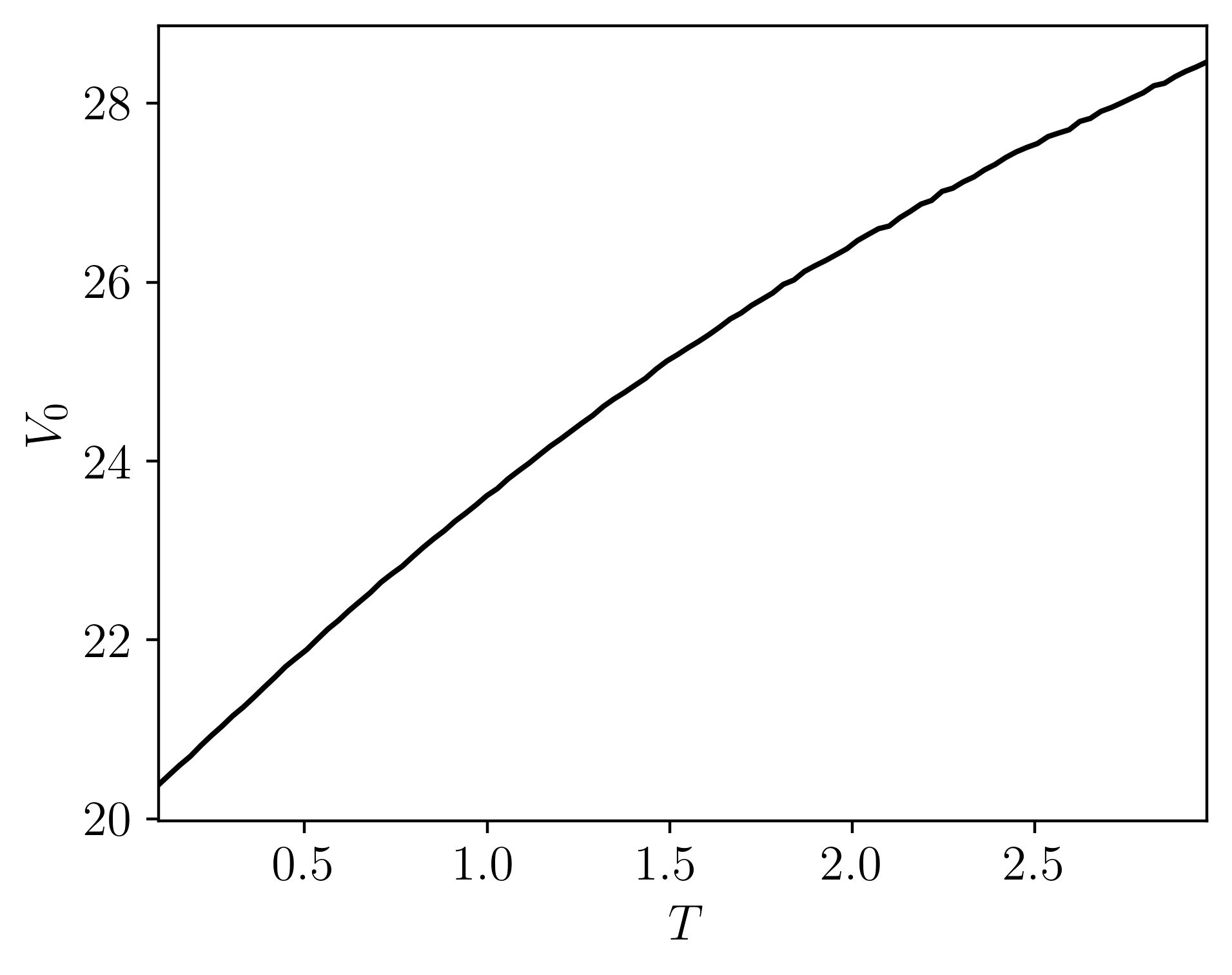
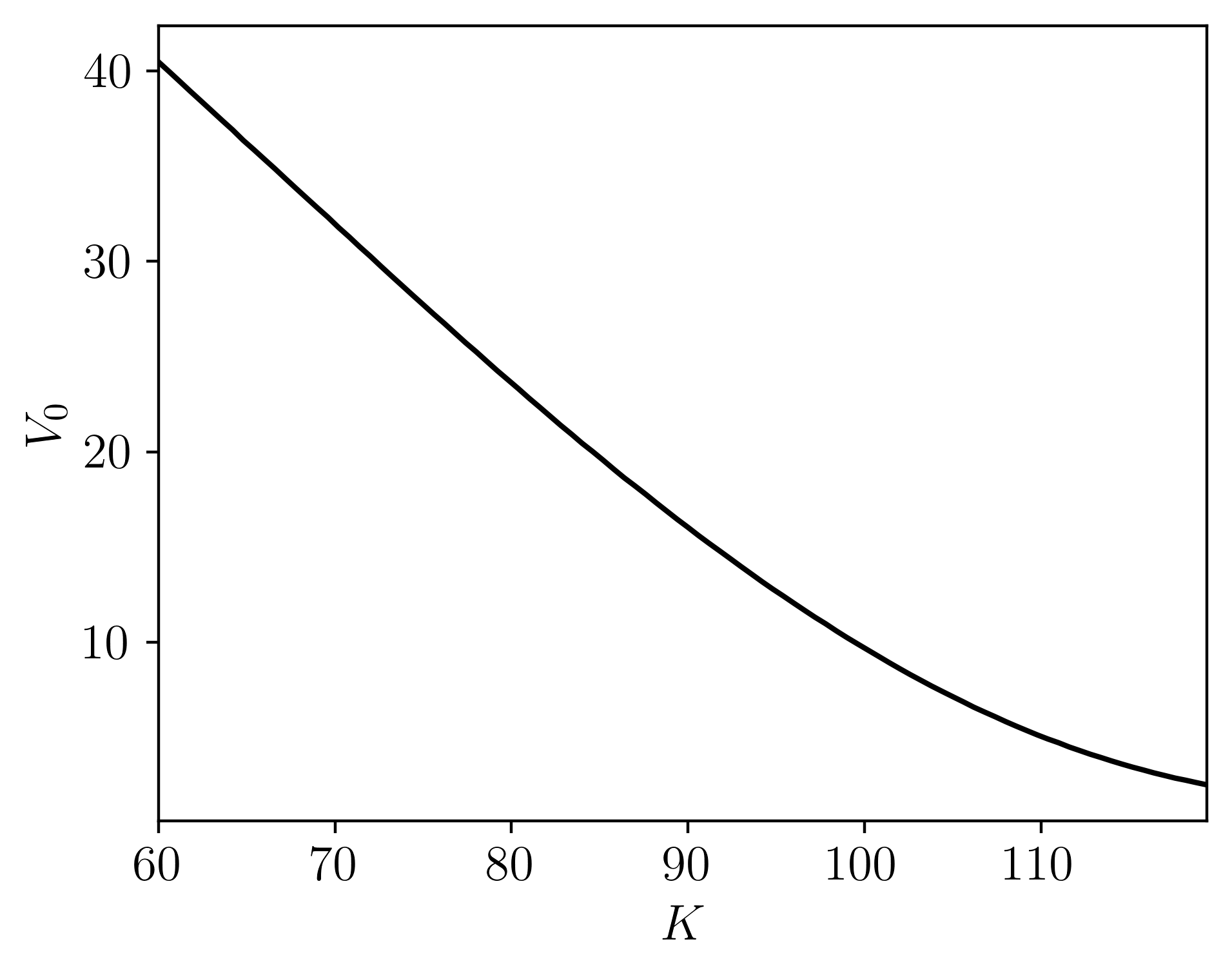
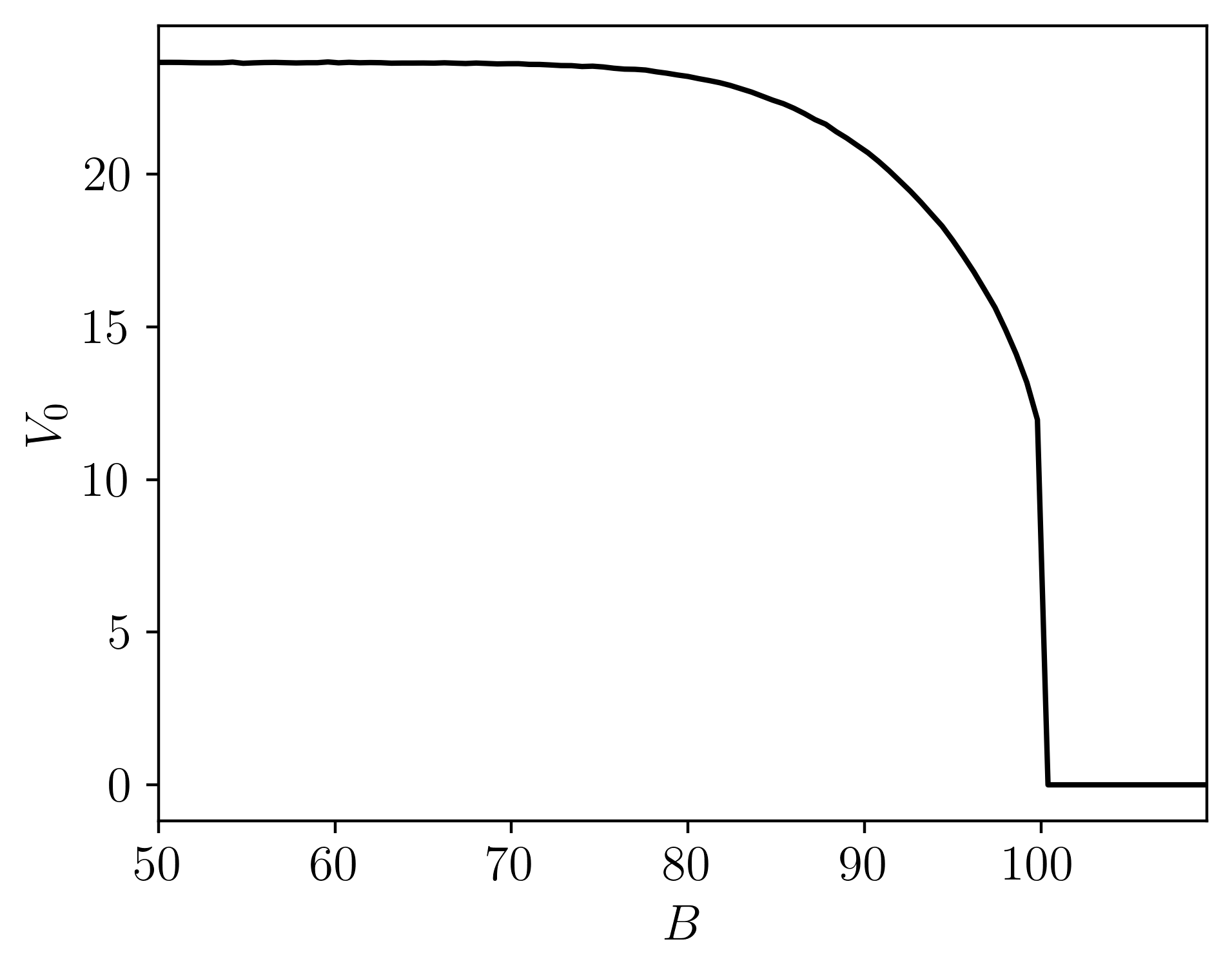
Pricing down-and-out European barrier options under the bilateral gamma model. Pricing done via Monte Carlo sampling with adaptive importance sampling, changing the measure of the process by adjusting the rates. Pricing is done in efficiently in parallel, written in C++.