-
Notifications
You must be signed in to change notification settings - Fork 13
Activation Functions Overview
Activation Functions used in (Deep) Neural Networks and their properties:
Note that there is no solid theory of how activation functions should be chosen. There are infinitely many possible activation functions. Which is the best for any given problem? It is unknown.
However, Glorot and Bengio (2010) investigated the effect of various activation functions with respect to the Vanishing Gradient problem and found these conclusions:
-
The more classical neural networks with sigmoid or hyperbolic tangent units and standard initialization fare rather poorly, converging more slowly and appar- ently towards ultimately poorer local minima.
-
Sigmoid activations (not symmetric around 0) should be avoided when initializing from small random weights, because they yield poor learning dynamics, with initial saturation of the top hidden layer.
-
The softsign networks seem to be more robust to the initialization procedure than the tanh networks, pre- sumably because of their gentler non-linearity.
-
For tanh networks, the proposed normalized initialization can be quite helpful, presumably because the layer-to-layer transformations maintain magnitudes of activations (flowing upward) and gradients (flowing backward).
-
Others methods can alleviate discrepancies between lay- ers during learning, e.g., exploiting second order information to set the learning rate separately for each parameter.
sharp step from 0 to 1. used by the Perceptron. not useful for non-binary problems
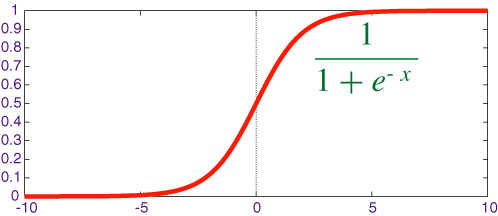
most basic function. soft (smooth) version of the step function
Problem: learning slowdown when output neurons saturate (i.e. are close to 0 or 1) when using the quadratic cost to train (because the derivative of the sigmoid becomes small near 0 or 1, which means small updates even when the error is really big). Using Cross-Entropy Cost Function helps, see http://neuralnetworksanddeeplearning.com/chap3.html#the_cross-entropy_cost_function
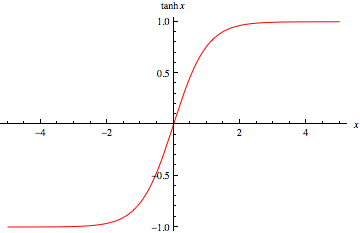
TanH Function: like Sigmoid but from [-1,1] instead of [0,1]
means that output data has to be re-scaled accordingly to [-1,1]
used when?
TL: The softmax function is a "transfer" function that "balances" (adjusts) the activations of other neurons given the input of one neuron, so that the activations of all neurons in a layer sum up to 1.
The output from the softmax layer can be thought of as a probability distribution.
The fact that a softmax layer outputs a probability distribution is rather pleasing. In many problems it's convenient to be able to interpret the output activation aLj as the network's estimate of the probability that the correct output is j. So, for instance, in the MNIST classification problem, we can interpret aLj as the network's estimated probability that the correct digit classification is j.
By contrast, if the output layer was a sigmoid layer, then we certainly couldn't assume that the activations formed a probability distribution.
see http://neuralnetworksanddeeplearning.com/chap3.html#softmax to try out the impact of the Softmax function with sliders
A unit employing the rectifier is also called a rectified linear unit (ReLU).
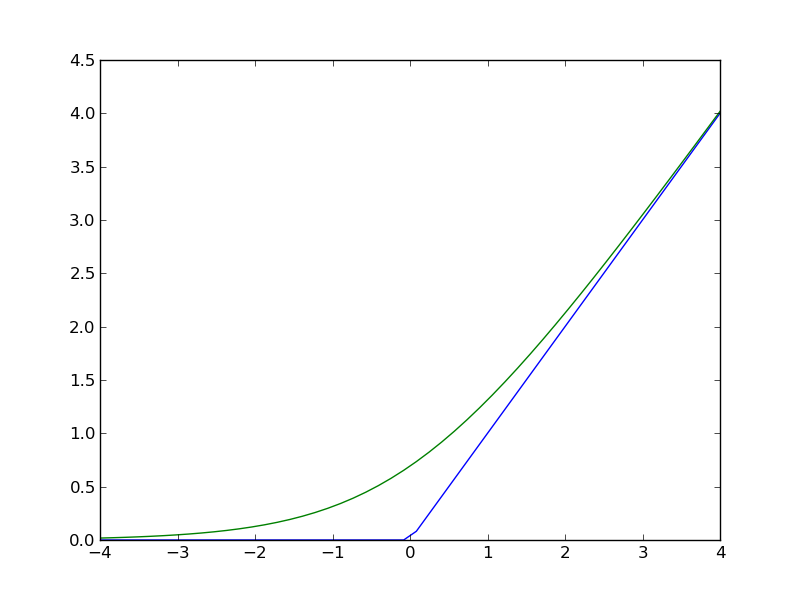
Rectifier Function: f(z) = max(0,z) , more precisely max(0,w⋅x+b), with input x, weight vector w, and bias b
(blue: Rectifier, green: Softplus (see below))
This activation function has been argued to be more biologically plausible than the widely used logistic sigmoid and its more practical counterpart, the hyperbolic tangent.
The rectifier is, as of 2015, the most popular activation function for deep neural networks.
https://en.wikipedia.org/wiki/Rectifier_(neural_networks)
For the first time in 2011, the use of the rectifier as a non-linearity has been shown to enable training deep supervised neural networks without requiring unsupervised pre-training. Rectified linear units, compared to sigmoid function or similar activation functions, allow for faster and effective training of deep neural architectures on large and complex datasets. The common trait is that they implement local competition between small groups of units within a layer (max(x,0) can be interpreted as competition with a fixed value of 0), so that only part of the network is activated for any given input pattern.
Advantages
- Biological plausibility: One-sided, compared to the antisymmetry of tanh.
- Sparse activation: For example, in a randomly initialized networks, only about 50% of hidden units are activated (having a non-zero output).
- Efficient gradient propagation: No vanishing gradient problem or exploding effect.
- Efficient computation: Only comparison, addition and multiplication.
These newer variations of the ReLU provide some advantages over the original ReLU:
- Leaky ReLUs allow a small, non-zero gradient when the unit is not active:
- ELU
- SELU
A smooth approximation to the rectifier is the analytic function
f(x) = ln(1 + e^x)
which is called the softplus function.
See green line in ReLU image above.
The derivative of softplus is f'(x) = 1 / (1 + e^{-x}), i.e. the logistic (sigmoid) function.
Activation functions are in close relation to the Cost function used!
E.g. a sigmoid has the learning slowdown problem when a quadratic cost function is used, but not when using cross-entropy cost. Also, a softmax output layer with log-likelihood cost can be considered as being quite similar to a sigmoid output layer with cross-entropy cost.
Given this similarity, should you use a sigmoid output layer and cross-entropy, or a softmax output layer and log-likelihood? In fact, in many situations both approaches work well.
As a more general point of principle, softmax plus log-likelihood is worth using whenever you want to interpret the output activations as probabilities. That's not always a concern, but can be useful with classification problems (like MNIST) involving disjoint classes.