Background knowledge for Bayesian Statistics and Maximum Likelihood Estimation

Resources

• Wikipedia: Prior Probability
• Wikipedia: Posterior Probability
• Wikipedia: Maximum Likelihood Estimation
• Youtube: 오토인코더의 모든 것 1/3, 2/3, 3/3
• My blog post(math formula displayed correctly)

Prior probability

The prior probability distribution of an uncertain quantity is the probability distribution about that quantity before some evidence is taken into account. This is often expressed as $$p(\theta)$$.

Posterior probability

The posterior probability of a random event is the conditional probability that is assigned after relevant evidence is taken into account. This is often expressed as $$p(\theta | X)$$. The prior and posterior probabilities are related by the Bayes' Theorem as follows:

$$p(\theta | x) = \frac{p(x|\theta)p(\theta)}{p(x)}$$

Maximum Likelihood Estimation (MLE)

MLE is a method of estimating the parameters of a statistical model, given observations. This is done by finding the parameters that maximizes the likelihood function; by selecting the parameters that make the observed data most probable. We can formulate this problem as follows:

$$\theta^* \in {\underset{\theta}{\text{argmax}} \mathcal{L}(\theta;x)}$$

where $$\theta$$ is the model parameters and $$x$$ is the observed data.

We often use the average log-likelihood function

$$\hat{\mathcal{l}}(\theta;x) = \frac{1}{n} \log \mathcal{L}(\theta;x)$$

since it has preferable qualities. One of this is illustrated later in this document.

Machine Learning in the MLE perspective

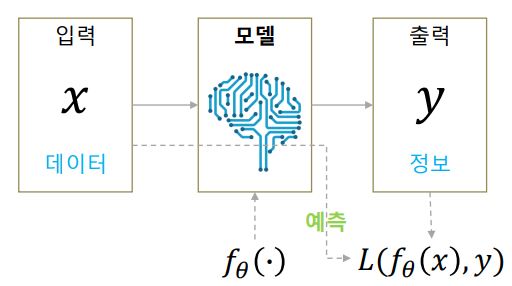
A traditional machine learning model for classification is visualized as the above: we receive an input image $$x$$ and our model calculates $$f_\theta (x)$$, which is a vector denoting the probability for each class. Then based on our label, we calculate the loss function, which is then optimized using gradient descent. Now, let us view this in a maximum likelihood perspective.

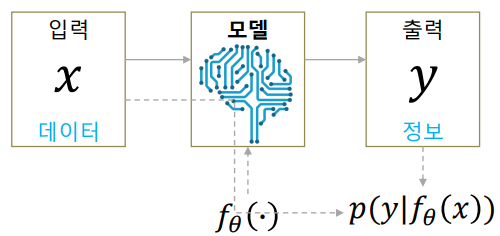
Now, when we create an ML model, we choose a statistical model that our output may follow. Then, our ML model function calculates the parameters of that statistical model. For example, let us assume that our output $$y$$ is one dimensional and has a Gaussian distribution. Then we set $$f_\theta(x)$$ to a two-dimensional vector and interpret it as

$$f_\theta(x) =\begin{bmatrix}\mu\\sigma\end{bmatrix}$$.

Thus for each input $$x$$ we obtain a Gaussian distribution for $$y$$. Using negative log-likelihood, our optimization problem is the following:

$$\theta^* = \underset{\theta}{\text{argmin}}[-\log p(y|f_\theta(x))]$$

If we assume that our inputs are independent and identically distributed (i.i.d), we can obtain the following:

$$p(y|f_\theta(x)) = \prod_i p(y_i|f_\theta(x_i))$$

Rewriting our optimization problem:

$$\theta^* = \underset{\theta}{\text{argmin}}[-\sum_i\log p(y_i|f_\theta(x_i))]$$

When we perform inference from our model, we no longer get determined outputs as we did in traditional machine learning models. We now get a distribution of $$y_\text{new}$$,

$$y_\text{new} \sim f_{\theta^*}(x_\text{new})$$

where we should sample a single $$y_\text{new}$$.

Loss Functions in the MLE perspective

Two famous loss functions, mean square error and cross-entropy error, can be derived using the MLE perspective.

(https://www.slideshare.net/NaverEngineering/ss-96581209)